電気回路理論/鳳-テブナンの定理

鳳-テブナンの定理(ほう-)あるいはテブナンの定理(Thévenin's theorem)は任意の2端子回路について成り立つ、次のような定理である。

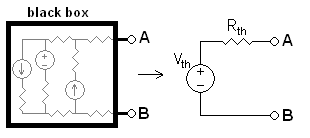
電圧源、電流源および抵抗からなり、2端子A、Bを持つ回路がある。ただし、必ずしも電圧源や電流源や抵抗は含まれていなくともよい。この時、回路の内部がどのように構成されているかに関わらず、次の方法によって1つの電圧源と1つの抵抗からなる等価電圧源を構成することができる。

端子AB間を開放した時にAB間に現れる電圧を $V_{0}$ とする。
2端子回路の中の電源を除去(電圧源ならば短絡し、電流源ならば除去・開放する)したときの端子ABから見た合成抵抗を $R_{0}$ とする。
このとき、この2端子回路は電圧 $V_{0}$ の電圧源と抵抗 $R_{0}$ の抵抗が直列に接続された回路と等価である。

証明は後ほど行うとして、まず具体的な使用法を見ることにする。

例題

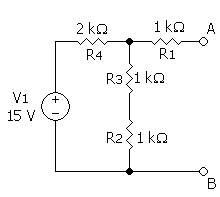
右図の回路のテブナン等価回路を求める。

この回路は1個の電圧源と4個の抵抗からなる。もちろんこのまま解析しても構わないが、なるべく単純な等価回路へ置き換えを行ってから解析を行いたい。そこで、鳳-テブナンの定理によって等価電圧源を求めることにする。

まず、端子ABを開放した時にAB間に現れる電圧を求める。ABを開放していれば抵抗 $R_{1}$ に電流は流れない(∵KCL)ので、点Aの電位は $R_{1}$ の左側の節点の電位と等しくなる。すなわちAB間の電圧は $R_{2},R_{3}$ にかかる電圧と等しくなる。電源、 $R_{4}$ 、 $R_{3}$ 、 $R_{2}$ からなる閉路の分圧回路を考えて、AB間に現れる電圧 $V_{0}$ は

V_{0}={\frac {R_{2}+R_{3}}{R_{2}+R_{3}+R_{4}}}V_{1}=7.5\mathrm {V}

となる。

次に、電圧源や電流源を除去した時に端子ABから見た合成抵抗を求める。右図から、合成抵抗 $R_{0}$ は

R_{0}=R_{1}+{\frac {1}{{\frac {1}{R_{4}}}+{\frac {1}{R_{2}+R_{3}}}}}=2\mathrm {k\Omega }

となる。

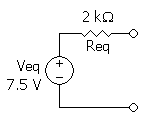
これより、この回路のテブナン等価回路は下図のようになる。

証明

鳳-テブナンの定理は重ね合わせの理を用いて容易に証明することができる。

まず、端子間に電圧源 $V_{0}$ と抵抗Rを直列に接続すると、ABの電位差は0だから電流は流れない。重ね合わせの理より、電圧源 $V_{0}$ を短絡したときと、二端子回路内の電源を除去したときに流れる電流の和が0になる。二端子回路内の電源を除去したときに流れる電流は $-{\frac {V_{0}}{R_{0}+R}}$ であるから、電圧源 $V_{0}$ を短絡したときには ${\frac {V_{0}}{R_{0}+R}}$ の電流が流れる。電圧源 $V_{0}$ を短絡したということは端子間に抵抗Rのみが接続されているということである。この電流の式をみると、二端子回路は電圧 $V_{0}$ と抵抗 $R_{0}$ が直列に繋がったものと等価である事がわかる。