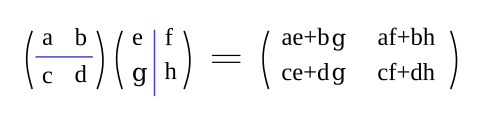旧課程(-2012年度)高等学校数学C/行列

高等学校数学C > 行列

---

本項は高等学校数学Cの行列の解説である。

連立一次方程式と行列

1次方程式

${\begin{cases}x+2y=1\\2x+3y=2\end{cases}}$

を、次のような記法で表してみる。

${\begin{pmatrix}1&2\\2&3\end{pmatrix}}{\begin{pmatrix}x\\y\end{pmatrix}}={\begin{pmatrix}1\\2\end{pmatrix}}$

これから勉強するのは、連立方程式とベクトルとの関係であり、それを考察しやすくするために、あらたに行列（ぎょうれつ）という量を導入する。

ベクトル ${\begin{pmatrix}x\\y\end{pmatrix}}$ に、 演算 ${\begin{pmatrix}1&2\\2&3\end{pmatrix}}$ を施して（この演算の内容こそが、これから説明する「行列」である）、 答えのベクトル ${\begin{pmatrix}1\\2\end{pmatrix}}$ を得た、という表現に書き換える。

まず、このような記法をするため、次に説明する行列（ぎょうれつ、英：matrix）という量を新たに定義する。

• 行列どうしの積

まず、行列どうしの積の定義を、

積　${\begin{pmatrix}a&b\\c&d\end{pmatrix}}{\begin{pmatrix}e&f\\g&h\end{pmatrix}}$

は、

行列　${\begin{pmatrix}ae+bg&af+bh\\ce+dg&cf+dh\end{pmatrix}}$

と等しい、と定める。
　 何故このように定めるのか、考えよう。
２つの連立方程式

${\begin{cases}ex+fy=p\\gx+hy=q\end{cases}}$

${\begin{cases}ap+bq=u\\cp+dq=v\end{cases}}$

において、中間的変数p,qを消去して、変数x,yに関する一つの連立方程式と書き直すと

${\begin{cases}(ae+bg)x+(af+bh)y=u\\(ce+dg)x+(cf+dh)y=v\end{cases}}$

となる。
　 実際、下2式のp,qに、上2式を代入して整頓すればよい。 読者は代入して確認せよ。
これを行列表現すると

${\begin{pmatrix}ae+bg&af+bh\\ce+dg&cf+dh\end{pmatrix}}{\begin{pmatrix}x\\y\end{pmatrix}}={\begin{pmatrix}u\\v\end{pmatrix}}$

他方、2つの連立方程式を行列を用いて書き直すと

${\begin{pmatrix}e&f\\g&h\end{pmatrix}}{\begin{pmatrix}x\\y\end{pmatrix}}={\begin{pmatrix}p\\q\end{pmatrix}}$

${\begin{pmatrix}a&b\\c&d\end{pmatrix}}{\begin{pmatrix}p\\q\end{pmatrix}}={\begin{pmatrix}u\\v\end{pmatrix}}$

上の式を下の式に、形式的に代入すると

${\begin{pmatrix}a&b\\c&d\end{pmatrix}}{\begin{pmatrix}e&f\\g&h\end{pmatrix}}{\begin{pmatrix}x\\y\end{pmatrix}}={\begin{pmatrix}u\\v\end{pmatrix}}$

２つの行列表現式を比較すれば、 行列の積の定め方の合理性が分かるだろう。
　

行列の定義の説明図

積の定義式は、一見すると複雑そうに見えるが、かりに補助線を

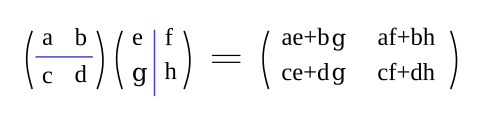
のように引いてみれば分かるように、たとえば合成後の2行1列め ${\begin{pmatrix}&\\ce+dg&\qquad \end{pmatrix}}$ は、合成前の2行めのそれぞれの成分 ${\begin{pmatrix}&\\c&d\end{pmatrix}}$ と、合成前の1列目 ${\begin{pmatrix}e&\\g&\end{pmatrix}}$の成分とを、掛けて足したものになっている。

一般に、積の合成後のx行y列めは、合成前のx行めのそれぞれの成分と、合成前のy列目のそれぞれの成分とを、掛けて足した結果になっている。

行列どうしの積は、順序によって結果が異なる。 たとえば行列A,Bを

$A={\begin{pmatrix}2&4\\3&3\end{pmatrix}}$

$B={\begin{pmatrix}7&9\\11&5\end{pmatrix}}$

とするとき、

それぞれ、

$AB={\begin{pmatrix}58&38\\54&42\end{pmatrix}}$

$BA={\begin{pmatrix}41&55\\37&59\end{pmatrix}}$

となる。

このように、一般の行列Aと行列Bの積は、一般に

$AB\neq BA$

となる。

上述の例は、2元連立一次方程式が式2個の場合に相当する行列だったが、一般に連立方程式の元の数は2個とは限らないし、方程式の数も2個とは限らないので、他の場合にも行列が定義できるように、行列の定義を拡張する。

つぎのように、数値を縦横に並べて、それぞれの段の文字の個数が等しいものを 行列（ぎょうれつ、英：matrix） と呼ぶ。

例えば、

${\begin{pmatrix}1&2&3\\4&5&6\\\end{pmatrix}}$

は行列である。

いっぽう、

${\begin{pmatrix}1&2&3\\&5&\\\end{pmatrix}}$

は、文字の個数が一致しないので、行列ではない。

行列の定義の説明図

行列の一部の、横に並んだ数値のかたまりを 行（ぎょう、英：row） といい、縦に並んだ数値のかたまりを 列（れつ、英：column） といい、それぞれの数値を 成分（せいぶん、英：element） と呼ぶ。

例えば、

${\begin{pmatrix}1&2&3\\4&5&6\\\end{pmatrix}}$

は2行、3列からなる行列である。

行数がmで、列数がnの行列を m×n行列 のように呼び、特に行数と列数が等しくnである行列ならば n次正方行列 と呼ぶ。

例えば、

${\begin{pmatrix}1&2&3\\4&5&6\\\end{pmatrix}}$

は 2×3行列 である。

第 i 行第 j 列の成分を (i, j) 成分という。

例えば、

${\begin{pmatrix}1&2&3\\4&5&6\\\end{pmatrix}}$

の (2, 1) 成分は4である。

• 「行列が等しい」とは

「2つの行列が等しい」とは、行数と列数が等しく、かつ対応する (i, j) 成分がすべて等しいことと定める。

つまり、 ${\begin{pmatrix}a&&b\\c&&d\\\end{pmatrix}}={\begin{pmatrix}e&&f\\g&&h\\\end{pmatrix}}$ 　とは、　$a=e,b=f,c=g,d=h$　である。

ベクトル内積と行列

ただ1行からなる行列を行ベクトル（ぎょうベクトル、英：row vector）といい、ただ1列からなる列ベクトル（れつベクトル、英：column vector ）という。

この行列の定義は、ベクトルの定義を拡張したものになっている。

たとえばベクトル（a、b）と(c、d)の内積 ac+bdは、行列の記法を使うと、

${\begin{pmatrix}a&&b\\\end{pmatrix}}{\begin{pmatrix}c\\d\end{pmatrix}}={\begin{pmatrix}ac+bd\end{pmatrix}}$

と書ける。

右辺の ${\begin{pmatrix}ac+bd\end{pmatrix}}$ は、1行1列の行列である。このように、行列では、1行1列の行列も認める。

行列の積の (i, j) 成分の値は、左側の行列の i 行のベクトルと、右側の行列の第 j 列のベクトルの内積である。

たとえば、行列$A={\begin{pmatrix}a&b\\c&d\end{pmatrix}}$ と $B={\begin{pmatrix}e&f\\g&h\end{pmatrix}}$ の積 $AB={\begin{pmatrix}ae+bg&af+bh\\ce+dg&cf+dh\end{pmatrix}}$ の(1, 2) 成分である $af+bh$ は、

ベクトル ${\begin{pmatrix}a&b\end{pmatrix}}$ と ベクトル ${\begin{pmatrix}f\\h\end{pmatrix}}$ との 内積になっている。

このように考えると、「行列」とは「ベクトルを並べたもの」とも言える。（ただし並べるベクトルの次元は同じ次元でなければならない。）

---

こうすれば、連立1次方程式を

${\begin{cases}ax+by=p\\cx+dy=q\end{cases}}$

は、行列を用いて

${\begin{pmatrix}a&&b\\c&&d\end{pmatrix}}{\begin{pmatrix}x\\y\end{pmatrix}}={\begin{pmatrix}p\\q\end{pmatrix}}$

と表せる。

例題

• 問

次のw, x, y, zの値を求めよ。

${\begin{pmatrix}1&2\\3&4\end{pmatrix}}={\begin{pmatrix}2w&3x\\4y&5z\end{pmatrix}}$

• 解答

それぞれ、

$w={1 \over 2},x={2 \over 3},y={3 \over 4},z={4 \over 5}$

行列の和，差，実数倍

行列の和・差・実数倍の定義は、次のように、ベクトルの和・差・実数倍と似たような性質を持つ。

行列の和の定義は、各要素ごとに足し合わせる、と定義される。

${\begin{pmatrix}a&&b\\c&&d\end{pmatrix}}+{\begin{pmatrix}e&&f\\g&&h\end{pmatrix}}={\begin{pmatrix}a+e&&b+f\\c+g&&d+h\end{pmatrix}}$

行列の差の定義は、各要素ごとに引くと定義する。

${\begin{pmatrix}a&&b\\c&&d\end{pmatrix}}-{\begin{pmatrix}e&&f\\g&&h\end{pmatrix}}={\begin{pmatrix}a-e&&b-f\\c-g&&d-h\end{pmatrix}}$

実数倍の定義は、各要素に実数を掛けることによって定義する。

$k{\begin{pmatrix}a&&b\\c&&d\end{pmatrix}}={\begin{pmatrix}ka&&kb\\kc&&kd\end{pmatrix}}$

(-1)A は -A と書く。

例題

• 問

行列A,B,Cを

$A={\begin{pmatrix}2&4\\3&3\end{pmatrix}}$

$B={\begin{pmatrix}7&9\\11&5\end{pmatrix}}$

$C={\begin{pmatrix}8&2\\13&15\end{pmatrix}}$

で定義するとき、

$A+B$

$C+B$

$C+A$

を計算せよ。

• 解答

それぞれ、

$A+B={\begin{pmatrix}9&13\\14&8\end{pmatrix}}$

$C+B={\begin{pmatrix}15&11\\24&20\end{pmatrix}}$

$C+A={\begin{pmatrix}10&6\\16&18\end{pmatrix}}$

となる。

零行列

すべての成分が0である行列を ゼロ行列（ぜろぎょうれつ、英：zero matrix） という。

${\begin{pmatrix}0&0&0\\0&0&0\\\end{pmatrix}}$ 　は ゼロ行列 である。

Aを行列、OをAと行数・列数が等しい零行列とすると、

$A+(-A)=(-A)+A=O$

を満たす。

行列の積

例題

• 問

上で用いた行列$A$,$B$,$C$について、

$AB$

$BA$

$BC$

$AC$

$CA$

を計算せよ。

• 解答

それぞれ、

$AB={\begin{pmatrix}58&38\\54&42\end{pmatrix}}$

$BA={\begin{pmatrix}41&55\\37&59\end{pmatrix}}$

$BC={\begin{pmatrix}173&149\\153&97\end{pmatrix}}$

$AC={\begin{pmatrix}68&64\\63&51\end{pmatrix}}$

$CA={\begin{pmatrix}22&38\\71&97\end{pmatrix}}$

である。

この結果から分かる通り、一般に行列の積は

$AB\neq BA$

となる。

$AB=BA$

となる場合、行列Aと行列Bは交換可能（可換）であるという。

単位行列

$E={\begin{pmatrix}1&0\\0&1\end{pmatrix}}$

を、2×2の単位行列（2次単位行列）と呼ぶ。対角成分だけが1であり、その他の成分がすべて0に等しい行列である。任意の2×2行列Aに対して、Eは

EA = AE = A

を満たす。

逆行列

行列Aに対してその行列との積が単位行列 $AA^{-1}=A^{-1}A=E$ となる行列 $A^{-1}$ を、その行列の逆行列と呼ぶ。そのような行列はもし存在すれば各Aに対してただひとつに定まる。もちろん一般にはAに対して右側からかけるか左側からかけるかによって積は異なるのだが、この場合はAに対して右からかけて単位行列になるのならば左からかけても単位行列になるし、逆もまたしかりであることに注意しておく。逆行列の逆行列はもとの行列に等しい。

2行2列の行列 $A={\begin{pmatrix}a&b\\c&d\end{pmatrix}}$ については、$ad-bc\neq 0$のとき $A^{-1}={\frac {1}{(ad-bc)}}{\begin{pmatrix}d&-b\\-c&a\end{pmatrix}}$ となる。 ad - bc = 0 のとき、逆行列は存在しない。

実際に行列の積を取ることで、これが正しいことが容易にわかる。

例題

• 問題

上で定めた行列$A$,$B$,$C$の逆行列を計算せよ。

行列A,B,Cは、それぞれ

$A={\begin{pmatrix}2&4\\3&3\end{pmatrix}}$

$B={\begin{pmatrix}7&9\\11&5\end{pmatrix}}$

$C={\begin{pmatrix}8&2\\13&15\end{pmatrix}}$

であった。

• 解答

それぞれ、

$A^{-1}={\begin{pmatrix}-{{1} \over {2}}&{{2} \over {3}}\\{{1} \over {2}}&-{{1} \over {3}}\end{pmatrix}}$

$B^{-1}={\begin{pmatrix}-{{5} \over {64}}&{{9} \over {64}}\\{{11} \over {64}}&-{{7} \over {64}}\end{pmatrix}}$

$C^{-1}={\begin{pmatrix}{{15} \over {94}}&-{{1} \over {47}}\\-{{13} \over {94}}&{{4} \over {47}}\end{pmatrix}}$

である。

逆行列を用いた連立一次方程式の解法

1次方程式

${\begin{cases}x+2y=1\\2x+3y=2\end{cases}}$

は、

${\begin{pmatrix}1&2\\2&3\end{pmatrix}}{\begin{pmatrix}x\\y\end{pmatrix}}={\begin{pmatrix}1\\2\end{pmatrix}}$

と書ける。両辺に左辺の行列の逆行列を掛けると、

${\begin{pmatrix}1&0\\0&1\end{pmatrix}}{\begin{pmatrix}x\\y\end{pmatrix}}={\begin{pmatrix}3&-2\\-2&1\end{pmatrix}}{\begin{pmatrix}1\\2\end{pmatrix}}\times (-1)$

${\begin{pmatrix}x\\y\end{pmatrix}}={\begin{pmatrix}1\\0\end{pmatrix}}$

x = 1, y = 0 が得られ、始めの連立1次方程式が解けたことになる。 一般に、連立1次方程式がただ一組の解をもつとき、連立1次方程式を解くことは逆行列を求めることと同じである。 特に、2×2行列の逆行列は既に公式が得られているので、2元1次方程式は簡単に解くことができる。

$A={\begin{pmatrix}a&&b\\c&&d\end{pmatrix}},\mathbf {x} ={\begin{pmatrix}x\\y\end{pmatrix}},\mathbf {b} ={\begin{pmatrix}p\\q\end{pmatrix}}$とおくと

$A\mathbf {x} =\mathbf {b}$

と書ける。ここでAをこの連立1次方程式の係数行列という。この方程式の解は、Aが逆行列を持つとき一意に定まり、 $\mathbf {x} =A^{-1}\mathbf {b}$ である。

行列の応用

図形への応用

点の移動

回転行列

平面上のベクトル${\vec {a}}$に対して回転行列 $R={\begin{pmatrix}\cos c&-\sin c\\\sin c&\cos c\end{pmatrix}}$ をかけた積$R{\vec {a}}$は、${\vec {a}}$を原点を中心にして角度cだけ回転させたベクトルになっている。

（証明）

ベクトルaを極座標を用いて$a=(r\cos \theta ,r\sin \theta )$と書く。すると積$R{\vec {a}}$は

$R{\vec {a}}={\begin{pmatrix}\cos c&-\sin c\\\sin c&\cos c\end{pmatrix}}{\begin{pmatrix}r\cos \theta \\r\sin \theta \end{pmatrix}}={\begin{pmatrix}r(\cos c\cos \theta -\sin c\sin \theta )\\r(\sin c\cos \theta +\cos c\sin \theta )\end{pmatrix}}=r{\begin{pmatrix}\cos(c+\theta )\\\sin(c+\theta )\end{pmatrix}}$

であり、これは確かに${\vec {a}}$を角度cだけ回転させたベクトルである。

一般の行列による点の移動

座標値（x,y）の点Pを行列をかけることで移動したものを考える。

${\begin{pmatrix}a&&b\\c&&d\end{pmatrix}}{\begin{pmatrix}x\\y\end{pmatrix}}={\begin{pmatrix}z\\w\end{pmatrix}}$

は、

$x{\begin{pmatrix}a\\c\end{pmatrix}}+y{\begin{pmatrix}b\\d\end{pmatrix}}$ とも書ける。

これは、新たな直線座標を用意し（新座標の各座標軸の単位ベクトルは前の座標を基準に測ると、それぞれ方向ベクトル ${\begin{pmatrix}a\\c\end{pmatrix}}$ および 方向ベクトル ${\begin{pmatrix}b\\d\end{pmatrix}}$ である。）、この座標に座標値（x,y）を代入することで点Pを移動したものを、前の座標系で測った場合の座標値になっている。

座標の変換

通常の直交座標（原点で90°で交わる座標）の上の点の座標（x,y）について、点の位置は同じまま、新たな別の直線座標（直交とは限らない）で見た場合の座標（z,w）を考える。新たな別座標（直線座標）は、計算の都合上、原点だけは元の座標と同じとする。すると、次のように、前の座標と新たな座標との関係を、行列で表記できる。

${\begin{pmatrix}a&&b\\c&&d\end{pmatrix}}{\begin{pmatrix}z\\w\end{pmatrix}}={\begin{pmatrix}x\\y\end{pmatrix}}$

というふうな関係式で記述できる。 実際に、たとえば (x,y)=(0,0) のとき （ z,w=0,0） となっている。

さて、左辺は $z{\begin{pmatrix}a\\c\end{pmatrix}}+w{\begin{pmatrix}b\\d\end{pmatrix}}$ とも書ける。

この式を、座標の変換の幾何学として考えた場合、次のような理論になる。

まず、新たな直線座標の座標軸の単位ベクトルの方向は、もとの座標系を基準に見ると、それぞれ方向ベクトル ${\begin{pmatrix}a\\c\end{pmatrix}}$ および 方向ベクトル ${\begin{pmatrix}b\\d\end{pmatrix}}$ である。

ここで、もし新たな座標系を基準にして、新たな座標軸の単位ベクトルの数値を見ても、結果の単位ベクトルの数値は （0,1） および (1,0) になるだけであり、何も計算した事にならない。なぜなら自己の座標系で自己の単位ベクトルを見ても、（0,1） および (1,0) でしかないから、である。

計算すべきは、新たな座標軸を基準にして前の座標軸を見た場合の数値、もしくは、前の座標軸を基準にして新たな座標軸を見た場合の数値である。

さて、この問題では点Ｐの位置（x、y）は何も変換しておらず、よって、前の座標を基準にして点Pの位置を見ても、何も変化しない。この問題で変更したのは座標軸のほうであるから、新たな座標系で見た点Ｐの値（z,w）に興味があるのである。

線の移動

平面図形上の線分は、2行2列の行列で変換できる。

$A={\begin{pmatrix}a&b\\c&d\end{pmatrix}}$ で変換した場合については、$ad-bc\neq 0$のとき、線は線に変換され、四角形は四角形に変換され、三角形は三角形に変換される。

面の移動

2行2列の行列 $A={\begin{pmatrix}a&b\\c&d\end{pmatrix}}$ については、図形の面積は、$ad-bc$倍される。

外部リンク

『高等学校数学科教材（行列入門）』文部科学省