高等学校工業 電子回路/増幅回路の基礎

トランジスタやダイオードは、温度が高くなると、抵抗が下がり、さらに電流が流れやすくなる。そして、電流が流れやすくなると、その電流による熱により、さらに温度が上がる。すると、さらに抵抗が下がるので、どんどん電流が流れてしまい、どんどん温度が上がってしまい、ついには、破壊されてしまうという、熱暴走が起きる危険がある。

このような熱暴走を起こさないため、さまざまな回路が考えられている。

自己バイアス回路

自己バイアス回路

自己バイアス回路は、つぎのような仕組みにより、熱暴走をふせいでいる。

1)　前提として、なんらかの理由で I_C が増加したとする。

↓

2)　すると、R_CI_C が増加するので、 V_CE＝VCC-R_CI_C により、 V_CEが減少する。

↓

3)　V_CEが減少したことにより、I_Bも減る。

↓

4)　ベース電流I_Bが減ったことにより、コレクタ電流も減るので、I_C が減る。

という仕組みで、熱暴走をふせぐ。

なお、この回路は「電圧帰還バイアス回路」（voltage feedback bias circuit）ともいう。

電流帰還バイアス回路

ブリーダ電流バイアス回路

1)　もしI_Cが増加すると、R_Eの両端の電圧 V_REも増加する。

↓

2)　すると、V_BEが減少するので（なぜなら V_BE＝V_B-V_REであり、後述するがV_Bは（ほぼ）一定なので。）、I_Bが減る。

↓

3)　I_Bが減れば、トランスジスタ出力側のI_Cも減る。

こういう仕組みで、安定化する。

ほとんどの回路の場合、I₁やI₂に比べて、I_Bは微小である。

なので、実用上は、ほとんどの場合、

I₁ ≒ I₂

である。 おおよそI₁が、I_Bの10倍以上なら、I₁ ≒ I₂と近似してよい。

このことから、電圧V_Eの大きさは、オームの法則により、ベース電圧が

$V_{B}={\frac {R_{2}}{R_{1}+R_{2}}}V_{CC}$

というふうに簡単に求まる。

そして、ベース電圧V_Bが一定値であるという事実が、さきほどの式から分かる。

こうして、仕組みの説明（2)で、V_Bがほぼ一定と見なせる、と言ったことの根拠が、証明された。

この回路は、安定性は高いが、抵抗による消費電力が大きいのが欠点である。

交流信号の増幅

バイパスコンデンサのある回路

増幅器は、入力信号のオン/オフの切り替えに、反応させやすい回路構造が、望ましい。

そして、スイッチなどを、オン/オフの切り替えをすると、電圧波形や電流波形は起伏ができるから、交流っぽい形になっていく。

ところで、コンデンサ素子は、交流電流を通す性質がある。なので、コンデンサは、交流信号を通す。

ならば、増幅器とコンデンサを組み合わせると、都合がいい。

交流信号を増幅するには、図のように、コンデンサを使えばいい。（※ 高校物理で習うように、）コンデンサは、交流電流を通す。

ただし、この回路図での交流電源の電圧の大きさは、直流電源の電圧 V_ccよりも、小さめにしておく必要がある。直流電圧よりも交流電圧 v_iを小さめにしておけば、交流電圧の波形の谷のぶぶんの状態でも、 つねに

V_cc＋v_i＞0

の状態になるので、 ベース電圧がつねにプラスなので、ベース電流を流しつづけられる。

図のように、R_Eに並列に加えるコンデンサC_Eをバイパスコンデンサ（by-pass capacitor）という。

C_Eは、R_Eの電圧変化による、増幅度の低下を防ぐ目的である。

なお、C₁は、交流電圧だけを通過させて、トランジスタのベースに渡すためのコンデンサである。

C₂は、トランジスタ出力のうち、交流電圧の成分だけを通すためのコンデンサである。

入力インピーダンス（h_ie）

• 
  トランジスタの静特性 (2SC1815)
• 
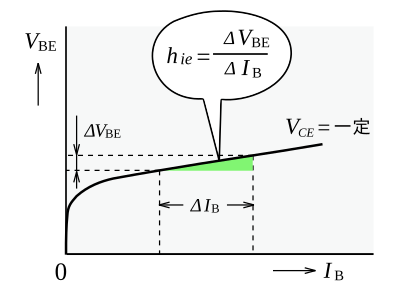
  入力インピーダンス h_ie の説明。
  傾きが分かりやすいように、やや大げさにグラフを描いてある。

---

トランジスタの静特性の第3象限のV_BE - I_B 特性を見てほしい。

$h_{ie}={\frac {\Delta V_{BE}}{\Delta I_{B}}}$

上式のh_ieによって、そのトランジスタの入力インピーダンス（input impedance）を定義する。

ベースの交流電圧をi_bとして、ベースエミッタ間に印加される交流信号をv_beとすれば、

$h_{ie}={\frac {v_{BE}}{i_{B}}}$

である。

また、この式を電圧についてまとめると、

$v_{BE}=h_{ie}i_{B}$

である。

電圧増幅率

トランジスタ回路の電圧増幅率 Av の定義は、入力電圧をviとして、出力電圧をvoとしたとき、

$A_{v}={\frac {v_{o}}{v_{i}}}$

で定義される。

さきほどの節で導入した入力インピーダンスを使って入力電圧を書き換えることができる。

$v_{i}=v_{BE}$

のことだから、つまり、

$v_{i}=v_{BE}=h_{ie}i_{B}$

よって

$v_{i}=h_{ie}i_{B}$

である。

入力インピーダンスで書き換えた入力電圧の式を、電圧増幅率の定義式に代入すれば、

$A_{v}={\frac {v_{o}}{h_{ie}i_{B}}}$

である。

図2.1　　エミッタ接地増幅回路

右図2.1のような回路の場合、

$A_{v}={\frac {v_{o}}{h_{ie}i_{B}}}={\frac {R_{L}h_{fe}i_{B}}{h_{ie}i_{B}}}={\frac {R_{L}h_{fe}}{h_{ie}}}$

よって、

$A_{v}={\frac {R_{L}h_{fe}}{h_{ie}}}$

と求まる。

なお電流増幅率 A_iは、定義式は

$A_{i}={\frac {i_{c}}{i_{b}}}$

である。つまり

$A_{i}={\frac {i_{c}}{i_{b}}}=h_{fe}$

である。

電力増幅率 A_Pは、定義式は

$A_{P}={\frac {P_{o}}{P_{i}}}$

である。つまり

$A_{P}={\frac {V_{CE}}{V_{BE}}}{\frac {I_{C}}{I_{B}}}=A_{v}A_{i}$

である。