中学数学2年 図形の調べ方
この章では、2年生の図形の学習の基礎を学びます。
直線と角
[編集]2直線が交わってできる角
[編集]
直線が2つ交わると、その交点の周りに、頂点を共有する4つの角ができます。
このとき、右図の∠a と∠c のような、正反対の向きに開いた2つの角を対頂角(たいちょうかく)といいます。∠b と∠d も対頂角です。
たとえば∠b が120°のとき、∠a と∠c の大きさを比べてみると、
- ∠a = 180°-120° = 60°
- ∠c = 180°-120° = 60°
つまり、∠a = ∠c となります。 これは、∠b が何度であっても成り立ちます。なぜなら、∠a も∠c も、(180-∠b )°になるからです。ですから、次のことが言えます。
| 対頂角の性質 |
| 対頂角は等しい。 |
2直線に1つの直線が交わってできる角
[編集]
2直線を横切るようにもうひとつの直線が交わるとき、8つの角ができます(右図)。
このとき、∠a と∠e のように、角の頂点から見たとき、同じ方位に開いた角を同位角(どういかく)といいます。∠a と∠e はどちらも、頂点から見て左上の方位に開いているため、互いに同位角といえます。∠b と∠f は互いに同位角であり、∠c と∠g は互いに同位角であり、∠d と∠h もそれぞれ同位角です。
また、∠b と∠h のように、2直線の内側にある2つの角で、それぞれの頂点から見たとき、正反対の方角に開いた角の組あわせを錯角(さっかく)といいます。右下の方位に開いた∠c と左上の方位に開いた∠e も錯角です。
平行線と同位角・錯角
[編集]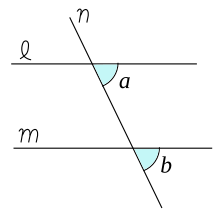
右図のように2直線が平行(へいこう)であるとき、同位角どうしは等しくなります。これは、平行線の基本的な性質として、しっかり覚えて下さい。また逆に、2直線の作る同位角が等くなっていれば、2直線は平行であることがわかります。これは、平行線の成立条件として覚えてください。
になっており、また、
になっていることがわかります。

錯角どうしも、2直線が平行なときには、錯覚の大きさも等しくなります。また、2直線の作る錯角が等しくなっていれば、2直線は平行だと見抜くことができます。
| 平行線と同位角・錯角 |
| 1, 2直線が平行であるとき、その同位角は等しい。また、錯角も等しい。 |
| 2, 同位角どうし、あるいは錯角どうしが等しければ、その2直線は平行である。 |
多角形の角
[編集]三角形の内角と外角
[編集]中学校数学では、主に円、三角形、四角形について学習します。2年生では三角形と四角形を主に学習します。まずは、三角形から調べてみましょう。
三角形の3つの内角(図形の内側の角)の和はいくつになるでしょうか。ここでは、平行線と角の性質を用いて調べていきます。

右図のΔABCに、辺BCの延長CDを引きます。
また、辺ABに平行で、Cを通る直線CEを引きます。
分かりやすいように、全ての角に右図のように名前をつけてみましょう。 このとき、平行線の同位角は等しいですから、
- ∠b = ∠e … (1)
また、平行線の錯角は等しいですから、
- ∠a = ∠d … (2)
∠c, ∠d, ∠e は一直線上にあるので
- ∠c + ∠d + ∠e = 180°
ですから、これに(1),(2)を代入する事により、
- ∠a + ∠b + ∠c = 180°
| 三角形の3つの内角の和 |
| 三角形の3つの内角の和は180゚である。 |

- 外角
外角とは、内角と隣り合った角のことで、右図の1のような角を指します。2のような角は指しません。

右図のように外角は1つの頂点につき大きさの等しい外角が2個あるが、普通はどちらか片方のことを言う。

外角には、次のような性質があります。
ある1つの三角形の頂点をA,B,C、それらの頂点に対応する3つの内角を ∠a, ∠b, ∠c とすると、
頂点Cの外角は、∠a + ∠b です。
なぜなら、さきほどの内角の和の説明の図で、
- ∠d + ∠e = ∠a + ∠bなので、
よって 頂点Cの外角は、∠a + ∠b です。
| 三角形の外角 |
| 三角形の1つの外角は、それと隣り合わない2つの内角の和に等しい |
多角形
[編集]
多角形の内角と外角の位置は、右図のとおり。 右図では例として五角形の場合をしめす。

n角形の内角の和は、 (nー2)×180 ° になる
なぜなら、n角形は、右図のように、(n-2) 個の三角形に分割できるからである。(なお、右図は七角形である。)

ただし中学のこれらの多角形の公式では、右図のような、へこんだ多角形については考えていない。
合同
[編集]三角形の合同
[編集]
右図のように、2つの図形が、その図形の位置や向きをかえるだけで、形と大きさをかえずに一致させることができる場合、その2つの図形は 合同(ごうどう) である、という。
三角形GHIも、三角形ABCを左右にひっくり返して位置をズラしただけなので、三角形GHIと三角形ABCは合同である。
合同な図形には、次の性質があります。
- 合同な図形の性質
- 合同な図形では、対応する線分どうしの長さが等しい。
- 合同な図形では、対応する角どうしの角度が等しい。
四角形以上の合同
[編集]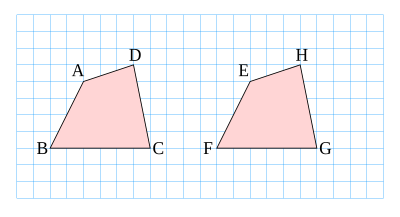
四角形や五角形といった四角形以上でも同様に、ある図形が「合同である」とは、その図形の位置や向きをかえるだけで、形と大きさをかえずに一致させることができる場合のことである。
右の図の例では、
- 四角形ABCDと四角形EFGHは合同である。
記法
[編集]三角形ABCと三角形DEFが合同の場合に、合同であることをあらわす記号≡を使って、
△ABC ≡ △DEF
のように書くことで、三角形ABCと三角形DEFが合同であることを記述したことになる。
なお、合同の記号 ≡ を使う時には、対応する頂点が同じ順番になるように書く。
たとえば、 △ABC ≡ △DEF なら、頂点AとDが対応、頂点BとEが対応、頂点CとFが対応、というふうに対応していると主張していることになる。
- 四角形や五角形などの場合の記法
四角形ABCDと四角形EFGHが合同の場合に、そのことを表す記法として、
四角形ABCD ≡ 四角形EFGH
のように書く。三角形の場合とちがい、四角形では、四角であることを表す数学記号が無いので、上式のように式中に日本語(「四角形」)を使ってもよい。
四角形以上の場合でも、対応する頂点が同じ順番になるように書く。
五角形以上の場合も同様に、式中に
五角形ABCDE ≡ 五角形 FGHIJ
のように、日本語を式中に使ってもよい。
合同条件
[編集]2つの図形が合同であるために、満たすべき条件を 合同条件(ごうどうじょうけん) という。
三角形
[編集]2つの三角形において、つぎの条件のいずれかが成り立つとき、その2つの三角形は合同である。

- 三角形の合同条件
- 2つの三角形は、次の3つの条件のどれかを満たす場合に、合同です。
- 3組の辺がそれぞれ等しい場合
- 2組の辺とその間の角がそれぞれ等しい場合
- 1組の辺とその両端の角がそれぞれ等しい場合
2個の三角形が、上記の3つの条件のいずれかを満たすと、その2個の三角形は合同である。 この3つの条件のことを 三角形の合同条件(さんかっけい の ごうどうじょけん) という。
三角形の合同条件はまた、三角形を作図する際に、その三角形の形を1通りにするための条件でもあります。 言い方をかえると、もし、ある三角形について、合同条件を満たせる辺や角度の情報が与えられたなら、その三角形と合同な三角形を作図できます。
証明の仕組み
[編集]証明(しょうめい)とは、すでに成り立つことがわかっていることを使って、成り立つかどうかわからないことが実は成り立つということを確かめること、その確かめの内容を人に説明することです。さっそく例を見てみましょう。
このような場合、問題の情報を整理します。情報を整理すると以下の通りです。
- 【仮定】 BC=DC , AC=EC
- 【結論】 AB=ED
問題の前提として与えられた条件を仮定(かてい)といいます。 つまり証明とは、仮定から結論(けつろん)を導くことです。結論を導くために、今回は△ABC≡△EDCを証明すればよさそうです。(記号≡は合同という意味) そのためには∠BCA=∠DCEであるか、AB=EDであることを確かめられればよさそうです。この場合は、対頂角の関係にあるので∠BCA=∠DCEであることがわかります。以上のことを、きちんと整理した形に書くのが証明です。 細かいことですが、証明が終了したら最後に必ず「ここで終わりです」という宣言をします。たとえば「(証明終)」や「//」や「Q.E.D」と書いたり、あるいは文章で「これで結論は証明された。」と書くなど、いくつかの書き方がありますが、ここでは「(証明終)」を用いることにします。
△ABCと△EDCにおいて仮定より
- BC=DC・・・①
- AC=EC・・・②
また、対頂角は等しいので
- ∠BCA=∠DCE・・・③
①・②・③より、対応する2辺とその間の角がそれぞれ等しいので
- △ABC≡△EDC
したがってAB=ED (証明終)
以上のような今回の証明の中身を簡単に表すと次のようにまとめられます。
【仮定】 問題に書いてある内容+自分で見つけた内容を整理する。
- ↓ ↓
- 合同条件により、合同な三角形が見つかる。
- ↓
- 【結論】合同な図形の性質により、結論が得られる。 (証明終)
三角形・四角形の定義の変更
[編集]「正方形は、長方形でしょうか?」
この疑問に、あなたは答えられますか?
もし「長方形」とは何であるかの条件を、「長方形とは、タテとヨコの長さが等しいとは限らず、すべての角度が90度の四角形のことである」としたら、 正方形もまた長方形の一種になります。なぜなら、この条件では「タテとヨコの長さが等しいとは限らない」としましたが、一言も「タテとヨコの長さが違う」とは言ってないので、タテとヨコの長さが同じであってもいいからです。
一方、もし「長方形とは、タテとヨコの長さが違っており、すべての角度が90度の四角形のことである」としたら、正方形は長方形でなくなります。
この「長方形とは、タテとヨコの長さが等しいとは限らず、すべての角度が90度の四角形のことである」という宣言や「長方形とは、タテとヨコの長さが違っており、すべての角度が90度の四角形のことである」という宣言のように、ある用語の意味をはっきりさせる説明のことを定義(ていぎ)といいます。
つまり、
- 「長方形とは、タテとヨコの長さが等しいとは限らず、すべての角度が90度の四角形のことである」
という主張は、長方形の定義を宣言したことになります。
また、
- 「長方形とは、タテとヨコの長さが違っており、すべての角度が90度の四角形のことである」
という主張も、長方形の定義を宣言したことになります。
議論などの際に、他人の書いた「証明」を読むさい、ときどき、言葉の意味が自分の使い方とは違っている場合があるので、必要に応じて、相手の人の証明での語句の定義を確認する必要があります。(※ しかし中学校レベルの議論や数学の場合は、教科書などが用語の意味を決めているので、定義を確認する必要性が少ない。)
ひとつの証明の中では、定義は一貫させる必要があります。
中学校以上の数学では(中学校での教育もふくむ)、証明の手間をラクにするためか、長方形の定義を「長方形とは、タテとヨコの長さが等しいとは限らない(等しくてもよい)、すべての角度が90度の四角形のことである」として、正方形を長方形の一種に含める場合があります。こうすれば、長方形について成り立つ公式などを証明した際に、正方形についても証明したことになるので、わざわざ正方形について別々の証明をする手間が省略できるからです。
同様に、中学校では、「二等辺三角形」を「正三角形」の特殊な場合とすることも、よくあります。
もし二等辺三角形の定義を「2辺以上の長さが同じ三角形である」(二等辺三角形の定義)とすれば、正三角形の3つの等しい辺も2辺以上という条件を満たすので( 3辺 ≧ 2辺 )、正三角形は二等辺三角形の特殊な場合であると分類できます。
また、長方形や三角形にかぎらず、高校や大学などで、いくつかの用語の定義が変わっている場合もあるので、あたらしい分野の学習の際には、その分野の言葉の定義を確認するようにしましょう。(あまり気にしなくても、普通の気のきいた教材なら、中学など下の学校とは用語の定義が違っている場合、読者に定義に変更のあることを説明しておいてくれる。とりあえず中学生は、高校・大学レベルに学習が進んだ将来、いくつかの用語の定義が将来的に更新される可能性もあることを、念頭においておけばいい。)
三角形についての証明
[編集]3組の辺がそれぞれ等しい場合
[編集]
ACという補助線を引くことにより、結論に登場する角を含むような三角形を作ることができます。
△ADCと△ABCにおいて仮定より
- AD=AB・・・①
- DC=BC・・・②
また、ACは共通だから
- AC=AC・・・③
①・②・③より、対応する3辺がそれぞれ等しいので
- △ADC≡△ABC
したがって∠B=∠D (証明終)
2組の辺がそれぞれ等しく,その間の角が等しい場合
[編集]1組の辺が等しく,その両端の角がそれぞれ等しい場合
[編集]角の分類
[編集]


直角三角形にかぎらず、ある角の角度が0°以上で 90° より小さい場合に、その角度を 鋭角 (えいかく)という。
ある角の角度が 90° 以上で180より小さい角度の場合に、その角を 鈍角 (どんかく)という。

図でみると分かるように、三角形では、どんな三角形でも最低限でも2つの鋭角がある。
また、直角では、鋭角でもなく鈍角でもないと分類するのが一般的である。
つまり、角度は、鋭角か直角か鈍角かの3通りのうちのどれかに分類される。
反例と逆
[編集]※ 指導要領のカリキュラム改訂で、中学2年の数学に「反例」が加わりました。とりあえず、幾何の単元に付け足します。
検定教科書を編集者がまだ調べていないので、当ページでは当面のあいだ、図形の例ではなく、代数計算を例に説明します。
図形でも反例や逆では下記と同様の理論が成り立ちます。
反例
[編集]たとえば、
- 「5の倍数は、かならず奇数である」
という主張があったとします。
もちろん、この主張は間違っています。
では、どうやって、この主張の間違いを見つければいいでしょうか。
たとえば、10 は 5 の倍数です。しかし 10 は奇数ではありません。10は偶数です。その証拠に、10÷2=5 で割りきれます。
このように、主張されていることの前提条件(この場合は「5の倍数である」)を満たしているのに、主張の後半(この場合は「必ず奇数である」)を満たさないものを反例(はんれい)と言います。
前提条件の部分は、必要に応じて文章を少し意訳して言い換える必要があります。たとえば、もとの文章
- 「5の倍数は、かならず奇数である」」
は、そのまま元の文章の前半分を抜き取ると
- 「5の倍数は」
のように途中で終わってしまうので、文章になっていないです。
この場合、同じ内容の文章を自分でつくり、
- 「ある数 m が5の倍数であるとする。この数 m は必ず奇数である。」
のように、2つの文章に分けます。
そして、それから前提条件「ある数 m が5の倍数である」と後半部分「この数 m は必ず奇数である」を作っていきます。
この例のように、証明において、主張されている内容によっては、もし反例のある主張の場合、反例を一つでも見つければ、それで証明になる場合もあります。
もっと言うと、「必ず~である」という主張は、もし一つでも反例が見つかれば、その主張は間違いだと証明できることになります。
また「必ず~である」という主張は、数学においては、「すべて~である」と言った場合と意味が同じです。
実際、さきほどの5の倍数の主張の例なら、
- 「ある数 m,n,p,q,・・・ がすべて5の倍数であるとする。こうして得られた数 m,n,p,q,・・・ はすべて奇数である。」
と言い換えることも出来ます。
主張「すべての~が□□である」が間違いだと証明したいなら、ひとつでも反例を見つければいいのです。
逆
[編集]主張「4の倍数は、かならず2の倍数である」は正しいです。
なぜなら、
4の倍数を 4p とした場合、
4p ÷ 2 = 2p なので2で割りきれるからです。よって、4の倍数は、かならず2の倍数です。
しかし、2の倍数は、4の倍数ではありません。
たとえば、
2は整数の範囲では 4 で割りきれません。
2÷4 =0あまり2
です。
このように、「4の倍数は、かならず2の倍数である」は正しいのに、「2の倍数は、かならず4の倍数である」は正しくないです。
ある主張の前提と後半を入れ替えたものを逆(ぎゃく)と言います。
たとえば、「4の倍数は、かならず2の倍数である」の逆は、「2の倍数は、かならず4の倍数である」です。
この例のように、逆は必ずしも正しいとは限りません。
※範囲外: 「逆は必ずしも真(しん)ならず」という格言があります。
では、逆は必ず間違っているのでしょうか。いいえ、逆も正しい場合もあります。
たとえば、「ある数mが3の倍数であり、5の倍数であるとする。この場合、ある数mは15の倍数である。」の逆は、
「ある数mが15の倍数であるとする。この場合、ある数mは3の倍数であり、5の倍数である。」となります。
実際に
m=15p と置いた場合、
15p÷3=5p
15p÷5=3p
のように、それぞれ割りきれます。このように計算などによって、証明をできます。
※範囲外: 「逆は必ずしも真(しん)ならず」という格言では、「しも」が入っていることに注意してください。「必ず真ならず」とは言っていません。
逆の概念は、数学だけでなく、法律など社会科のような分野でも使えます。
たとえば、
「日本国民なら、必ず人間である。」という主張は、たぶん正しいでしょう。あるいは、「必ず」が断定しすぎだと思うなら、「現代では確率90%以上で」とかに言い換えてください。
説明を短くするため、とりあえず「必ず人間である」という主張だとして解説を進めます。
さきほどの「日本国民なら」の主張の逆は、
- 「人間なら、必ず日本人である。」
という主張になります。もちろん、アメリカ人とか韓国人とかを考えれば、この主張が間違いであると、すぐに分かります。
アメリカ人も韓国人も当然に人間ですが、しかし彼ら彼女らは日本人ではないのが普通です。(二重国籍とかの人を考えた場合ですら、「人間なら、必ず日本人である」の主張は間違いです。)
この例だけだと、法律との関係が分からないでしょう。しかし、たとえば、下記のような主張をする外国人がいたとしましょう。
- 「私はアメリカ在住のアメリカ人です。私はパスポートも日本滞在ビザも持っていません。しかし私は人間ですので、よって私は「人間なら、必ず日本人である。」という言葉のように人間でもあるので、よって私は日本人でもあります。だから私はパスポートなしでも日本に入国していいのだ。」
と言い張るアメリカ人がいたら、どこが論理的に間違っているか、ちょっと考えれば分かります。(その人が本当にアメリカ人かどうかは、ひとまず考えないでおく。)
「人間なら、必ず日本人である。」が間違いですので、それ以降の彼の主張は、基本的に価値がありません。
現実の法律問題はこのように単純ではなく、もっと複雑だったりもしますが、しかし法律においても、「逆」などの概念は必要です。


