中学数学2年 四分位範囲と箱ひげ図

中学校の学習 > 中学校数学 > 中学数学2年 > 中学数学2年 四分位範囲と箱ひげ図

四分位数

データを大きさの順に並べた時、下位から、${\frac {1}{4}}(25\%),{\frac {1}{2}}(50\%),{\frac {3}{4}}(75\%)$に当たる数値をそのデータの四分位数(しぶんいすう)と言う。特に下位から25%に当たる数値を第1四分位数、 下位から75%に当たる数値を第3四分位数という。下位から50%に当たる数値は第2四分位数と言うこともできるが、中央値のことである。なお、これらを$Q_{1},Q_{2},Q_{3}$と表すこともある。

データ1の四分位数を求めてみよう。まずは資料を小さいほうから順に並べかえる。

• データ1

順位	10		9		8		7		6		5		4		3		2		1
体重（kg）	53.6		55.8		56.1		57.9		60.3		62.7		63.1		65.4		67.1		70.0

まずは中央値を求めてみよう。前でも説明した通り、この資料の中央値は5番目と6番目の平均である61.5kgである。

第1四分位数はこの資料では順位が6番目～10番目の中央値とも考えられる。つまり、8番目の値となるので56.1kgとなる。

第3四分位数も同様に順位が1番目～5番目の中央値と考えられるので求める数値は3番目の値の65.4kgである。

なぜ四分位数を使うか

統計には「平均」という概念があるのに、なぜ「中央値」や、「四分位」のQ2という概念を使うのだろうか。

それは、平均は、極端な値に大きく左右されやすく、実態を反映したものとは言えない可能性があるからである。

例えば、日本における二人以上の世帯の負債について考えよう。 日本における二人以上の世帯のうち61.5%は負債を有していないが、二人以上の世帯の負債の平均値は572万円である。これは、一部の世帯が負債を多く所有しているため(負債保有世帯での負債の平均値は1486万円)、これが平均が大きく押し上げている。

このように、平均値は極端な値に大きく左右されやすいという性質がある。従って、中央値を使うとこのような場合の実態が把握しやすくなる。

次にバラツキの大きさについて考えてみる。

中央値によって極端な値の影響を排除できるので、ばらつきの計算でも、中央値の付近だけのばらつきを計算すれば極端な値に左右されにくい指標として使える。

これが四分位偏差の意義である。

こういう意義さえ分かれば、後述の「四分位範囲」がなぜQ3（第3四分位数）とQ1（第1四分位数）との差なのかも、おのずと分かるだろう。

四分位範囲

第3四分位数と第1四分位数の差を、そのデータの 四分位範囲(はんい) という。

データ1の四分位範囲は $65.4-56.1\,\mathrm {kg}$となる。

※ 中央値付近のデータがどんだけ散らばっているかだけを見たい場合に、四分位範囲が便利である。出典は総務省『統計学習の指導のために』。

「範囲」と「四分位範囲」はちがう

「範囲」と言った場合、これは最大値と最小値の差である。

「範囲」の特性として、上述の架空の独裁国家の経済統計の例のように、極端に値の大きい例外的なデータがあると、それによって範囲は強く影響をうけてしまう。

そこで、新たな指標が必要であり、例外的なデータの影響を受けづらい、それでいて「範囲」のようなものが必要になる場合もある。

そう、それこそが「四分位範囲」である。だから四分位範囲は、もし統計データに、例外的に極端に大きい最大値あるいは極端にマイナスの大きい最小値があっても、その影響を受けづらい。

四分位偏差

四分位範囲の半分のことをその資料の四分位偏差(へんさ)と言う。四分位偏差が大きいほど、データの散らばりが大きいといえる。

資料1の四分位偏差は${\frac {65.4-56.1}{2}}=4.65\,\mathrm {kg}$となる。

箱ひげ図

次の図のようにデータの分布を四分位数を用いて見やすくしたものを箱ひげ図と言う。

箱ひげ図の読み方

1. 長方形の箱の左端が第1四分位数、右端が第3四分位数である。
2. 長方形の箱の中の線分が中央値を表している。
3. 長方形の箱の両端から伸びている線分の端っこが（外れ値を外した場合の）最大値、最小値を表している。
4. 「+」という印を使い、平均値を示すこともある。
5. 明らかな外れ値は点で表す事がある。

箱ひげ図

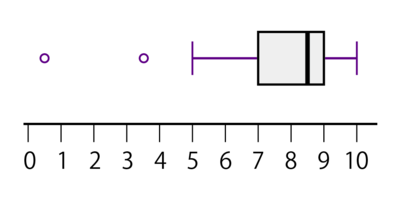
演習問題
上の箱ひげ図の最小値、最大値、四分位数をそれぞれ求めよ。

解答

• 最小値は一番左の点の値なので、0.5。
• 第1四分位数は箱の左端の範囲なので、7。
• 中央値は箱の中の線分の値なので、8.5。
• 第3四分位数は箱の右端の部分なので、9。
• 最大値は右端のひげの値なので、10。