中学数学1年 比例と反比例
比例・反比例のグラフ
[編集]グラフの基礎
[編集]
数学ではグラフを書くときに、右の図のような格子状の平面を用いる場合が多い。このような数の割りふられた格子状の平面を座標平面(ざひょうへいめん)といい、これをグラフ用紙として利用する。本来、座標平面とグラフ用紙は用途の異なる別々の存在だが、見た目の区別がつかないことからしばしば混同され、共通の用語で表現される場合がある。小学校でも「グラフ」を学んだと思われるが、中学校では負の数も考えるので、上・右だけでなく、左、下へとも広がっている平面として考える。グラフの横の数直線をx軸(エックスじく)、縦の数直線をy軸(ワイじく)と呼ぶ。2本の座標軸はそれぞれ値0に対応する点で直交させる。この点、x = 0, y = 0 を表す点で、原点(げんてん)と呼ぶ。ふつう記号 O (オー)で表す(ゼロではない)。原点はx軸とy軸の交わる点にある。因みに平面座標上のOはorigin(オリジン)を意味する。オリジンは「原点、基点」を意味する。
この章のタイトルは『比例・反比例のグラフ』だが、これら「座標平面」や「原点」・「x軸」・「y軸」などの用語は、比例や反比例の形のグラフにかぎらず、どんな形のグラフでも、右図のようにタテとヨコに一定間隔に数直線がある場合には分野を越えて共通に使われる用語である。座標は平面座標の他にも、複素平面(ガウス平面)や平面直角座標などがある。

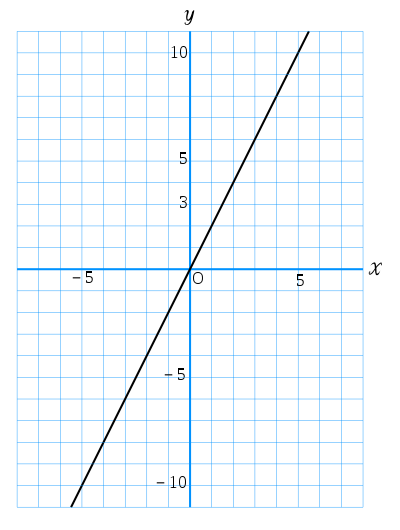
座標平面の使い方の例として、右図に方程式 2x-y=0 を満たす2数の順序対(x,y)が、座標平面上の直線を形作る例をしめす。
また、原点をあらわす記号Oは、式の直線と重ならないように、少しだけ位置をズラして書き込むことが一般によく行われている。

右図に y = -2x の式であらわされる直線を座標平面であらわした例をしめす。
右図の例からも分かるように、 y=ax の形の式で係数aが 負の数 の場合は、右下がりの直線になる。
また、さきほどの y = 2x のグラフを思い起こせばわかるように、 係数aが 正の数 の場合は、右上がりの直線になる。

の例を右図にしめす。このように、y=ax の係数 a が分数や小数であっても座標平面を使ってよい。

また、分数を係数にもつグラフは、右図の のグラフのように、たとえば を xの係数 として持つなら、x軸方向(右)に2進むたびにy軸方向(上)に3進んでいる。
右図のように座標のサイズは自由であり、マス目が等間隔ならば、縦長でもいいし、横長でもいい。 ただしx座標にもy座標にも負の数(-の数)がある。

右の図は、座標上に点を取った様子である。点Aは、原点から右に4、上に3進んだところにある。そこで、この点の位置を表すときには、次のように表す。
- A(4,3)
一般に、原点から右にx、上にy進んだところにある点の座標を
- (x,y)
と書く。
もし、その(x,y) にある点が、点Cならば
- C(x,y)
のように書く。
このとき、xをその点のx座標(エックスざひょう)と呼び、yをy座標(ワイざひょう)と呼ぶ。つまり、点Aのx座標は4であり、y座標は3といえる。
また、図の左下にある点 B の座標を表すことを考えてみると、これは原点から左に2つ、下に3つ進んだところにある。これは、負の数で言い換えると、右に-2、上に-3進んだところにある。よって、点 B の位置は「座標が (-2, -3)である」もしくは「x座標が -2、y座標が -3である」と言える。
原点Oの座標は (0,0) である。
用語
[編集]- x軸(横軸)
- 原点から左右に伸びた数直線(軸)、y=0 の点から成る。
- y軸(縦軸)
- 原点から上下に伸びた数直線(軸)、x=0 の点から成る。
- 座標軸
- x軸,y軸を合わせた言い方
- 原点
- 座標平面の中心の交点 (記号で
0 と表す) - x座標
- 点の位置を、横軸(x軸)で読み取った値。
- y座標
- 点の位置を、縦軸(y軸)で読み取った値。
- 点の座標
- 点の位置をx座標とy座標の2値の順序対で表したもの。(x, y)で書き表す。
| 第一象限 | 第二象限 | 第三象限 | 第四象限 | |
|---|---|---|---|---|
| x座標 | 正 | 負 | 負 | 正 |
| y座標 | 正 | 正 | 負 | 負 |

関数
[編集]例えば、空の風呂に水を入れるとき、水の深さは水を入れ始めてからの時間にともなって変わる。 x 分後の水の深さを y cmとすると、x , y はいろいろな値をとる。
この x , y のように、いろいろな値をとる文字を変数(へんすう)という。
ある量と、そのある量にともなって変わる他の量があり、それぞれを変数 x , y で表すとき、x の値を決めるとそれにつれて y の値もただ1つに決まることを、 y は x の関数(かんすう)であるという。例えば上の例のyはxの関数である。
二つの変数が比例の関係にあるとは 等式 y =ax が成り立つことをいい、この式の中でx と y が変数、a が比例定数である。このように、関数である2数の値を等式で示したものを、関係式(かんけいしき)という。関数の全てが関係式を持つわけではないが、中学数学では関係式を持つ関数を主に学んでゆく。関数を決定するとは、関係式を明らかにすることを指す場合が多い。また、学年ごとに異なる形の関係式を持つ関数について学習を進めて行く。小学校では比例する2数の関係を、片方の変数が2倍, 3倍, ……, n倍になると、もう片方の変数も2倍, 3倍, ……, n倍になると定めたが、数学ではこれを比例の持つ性質のひとつと考え、上に示した形の関係式を持つx と y を、比例の関係と定義する。
注意: 数学では上記の式のように、変数や文字定数、方程式で出てきたような未知数を、ひとつの式の中で同時に文字で表すことがある。上記の式では、x と y が変数で、a が文字定数である。文字の種類によって、変数、文字定数、未知数の使い分けが特に決まっているわけではないので、式を読むときにはどの文字が変数でどの文字が定数として使われているかを意識し、よく確認しておこう。
比例の関係にある変数の例
[編集]- 時速 60km で走る車が x 時間かけて進む距離を y kmとしたとき、y = 60 x である。
- 1個あたりの重さ 100グラム のみかん x 個の合計の重さを y グラムとしたとき、y = 100 x である。
反比例のグラフ
[編集]
比例はy=axの形の関係式を持つ変数x,yの関数関係を指したが、
これに対し、xy=aすなわち、
- (aは定数)
の形の関係式を持つ変数x,yの関数関係を、反比例(はんぴれい、英:inverse proportion)とよぶ。反比例では、 片方の変数が2倍,3倍,……,n倍になると、もう片方の変数は 倍, 倍, ……, 倍となる関係を持っている。
この式の場合、yはxに反比例するという。慣習上、反比例の場合でもaは「比例定数」(ひれいていすう)という。 y=axと同様、この反比例の式 の場合も「yはxの関数である」といえる。
反比例では、その定義から、xとyの積が常に一定(どちらかが0である時を除く)になる。
反比例になる例
[編集]- 10リットルのジュースをx人で等分した一人分がyリットル
- 面積が50の長方形の縦の長さがx cmのとき横の長さがy cm
比例・反比例の利用
[編集]比例の利用
[編集]比例を利用した問題である。
くぎ20本の重さは50gでした。くぎ150本の重さを求めなさい。
くぎの重さはくぎの数に比例するため、くぎの1本の重さをy g とすると、
- 20y=50
という一次方程式に直せる。この方程式を解くと、となる。 これは1本あたりの重さなのでyで全体の重さを表し、くぎの本数をxで表すとという比例の式ができる。
問題の場合、150本の場合の重さを求めるので、式にx=150を代入する。
すなわち375g、ということになる。
反比例の利用
[編集]反比例を利用した問題である。
面積が30の長方形を作りたい。横を8cmとするとき、縦は何cmにすればいいか。
面積をある一定の数に定める場合、長方形の縦と横の長さは反比例する。縦の長さをyとすると、
(8y = 30)
すなわちcm、ということになる。
グラフの範囲(発展)
[編集]次のような問題を考える。
ここにたくさんのお湯の入った湯船がある。

湯船の注湯速度を毎分 xℓとする。また、2 分後の湯船のお湯の増加量を yℓとすると、
- y = 2x
となる。この式のグラフは右図の青い直線である。
さて、問題文より、xは
- -2 ≦ x ≦ 1
の範囲の値しかとることができない。 この領域をグラフに表すと、グラフの水色に塗りつぶされた領域となる。
よって、xが動く範囲を考えるとyのグラフはPからRまでの太い青の線分となる。
したがって、グラフを見るとyが動くことができる範囲は -4 ≦ y ≦ 2 であることが分かる。つまり、-4ℓ減少~2ℓ増加の範囲で増減することがわかる。
このように、変数にはとることのできる値の範囲に条件がある場合がある。 とることのできる値の範囲を、その変数の変域(へんいき)という。
※ 中1の範囲
[編集]yはxの関数であるとは、xの値を決めるとそれに対応するyの値が1つだけ決まることを指す。これを、xの関数yと表現することもある。よく検定教科書などで、 ともなって変わる2つの変数x,yがあって、… という記述を見かけるが、これは正しくない。xの値が変化したとき、これにともなってyの値が変わらなくても(例えば、常に y=3 の場合)、「yの値が1つだけ決まる」という条件にはあてはまるので、yはxの関数であるといえる。この関数は定数関数と呼ばれ、yの値に変化が見られないのでつまらないと思うかもしれないが、後に学ぶ継ぎ接ぎ関数の中で、しばしば見られるポピュラーな関数の一つである。
関数とは
[編集]たとえば、小学校などで一日の気温の変化を1時間ごとに観測した折れ線グラフでも、xを時間、yを気温とすれば、xの値を決めるとそれに対応するyの値が1つだけ決まる。
このように、xの値を決めるとそれに対応するyの値が1つだけ決まる場合、この関係を関数(かんすう)であるという。
関数とは何かについて、さきほど「xの値を決めるとそれに対応するyの値が1つだけ決まる」と説明したが、実はこの決まりさえ守れば、関係式で表せなくても関数である。(たとえば、気温の例では、yの値をxの値から求める計算式はない。)
このように「xの値を決めるとそれに対応するyの値が1つだけ決まる」とだけ関数の要件を決めておくことにより、数式であらわせないものであっても、必要に応じて関数として利用できるので、活用しやすくなる。
また、この気温の折れ線グラフの例からも分かるように、関数は折れ線であってもいいし、一次式や文字式であらわせなくてもいい。
そして重要なこととして、「xとyの関係を一次式や文字式などの数式であらわせなくてもいい」ということは、「関係を数式であらわせてもいい」ということである。
なので、正比例や反比例などの比例関係も、関数であるといえる。
なお、中学二年で習う「一次関数」とは、xとyの関係が一次式で表せる場合である。
関数の変域
[編集]気温の折れ線グラフでは、気温を測定してない時間帯には、当然、関数が存在しない。
たとえば、その日の朝6時から夕方5時まで気温を測定したら、そのあいだの時間だけが、関数の値が存在する時間帯である。
この、気温グラフで気温測定した時間帯のように、関数の値が存在する変数の領域のことを変域(へんいき)という。
なお、文字式であらわせる関数にも変域のある場合がある。
たとえば、反比例の式の関数
では、x=0 の部分は、変域から外れる
一次式であらわせる式でも、文章題などの応用問題では変域が存在する。 たとえば
窓があります。窓の高さは90 cmとします。窓を x cmあけたときの、あけられた部分の面積 y (単位はcm2とする)は、いくらでしょうか?
という問題では、
y = 90x
と式で表せるが、 窓のあけられた長さを0よりも小さくはできないし、窓の可動範囲までしか窓を開けないので、xに上限も存在する。
さいごに
[編集]中学1年で習う『関数』の単元は入門的な内容のため、数式であらわせる関数については中学1年では「比例」や「反比例」といった、単項式またはその逆数であらわせる関数だけをあらわしており、関数の概念を使わなくても式を解けるため、わざわざ「関数」という概念を構築する必要性が分かりづらい。
しかし、本来の関数とは、たとえ、もしyの式がxの二次式または二次より大きい次数の数式であっても、それが条件「xの値を決めるとそれに対応するyの値が1つだけ決まる」という条件を満たしているならば、その場合「yはxの関数である」である。逆に言えばこのページの単元「比例、反比例」の比例とも関連する。つまり関数は研究していくと簡単に解く方法が見つかるかもしれない。
最終的に読者が中学3年や高校で習う関数の理論は、このような、xについての二次式以上のyの式でも関数としてあつかう理論である。

















