旧課程(-2012年度)高等学校数学A/集合と論理

集合と論理[編集]

集合とは[編集]

中学では、たとえば「自然数のあつまり」とか「9以下の自然数のあつまり」とか「負の整数のあつまり」のようなものを、集合（しゅうごう）と読んできた。

では、数学でいう「集合」とは何か、これから考えていこう。

数学では、ある集まりのうち、さらに、それに属しているか属してないかを明確に区別できる条件のある物のあつまりを集合（しゅうごう、英：set）という。例えば、「自然数」は「n > 0となる整数n の全体」という区別可能な条件があるので集合といえる。

しかし「大きな数」というあつまりは、どこからが「大きな」数といえるのかがはっきりしないため、数学の「集合」ではない。

ただし、「大きな数」を例えば「1億以上の整数」と区別できるように定義すれば集合になりえる。

さて、数学的な「集合」を構成するもの一つ一つのことを、その集合の要素（ようそ、英：element）という。

たとえば、「自然数の集合」の要素なら、自然数1や自然数2や自然数3、・・・などのひとつひとつの自然数がそれぞれ要素である。

「 1 は自然数の集合の要素である」といえる。

「 27 は自然数の集合の要素である」といえる。

例
7以下の自然数の集合の要素は、1と2と3と4と5と6と7 である。

（※ 範囲外？）なお、数学的には、区別がはっきりしさえすれば、例えば「△△高校の今の3年B組の生徒全員」等も集合として考えることができる。かならずしも「集合」とは「自然数」や「整数」などの数でなくてもいい。

集合や要素の関係の表し方[編集]

集合と要素[編集]

aが集合Aの要素であるとする。このとき、aは集合Aに属する(ぞくする)といい、記号で、

a ∈ A

または逆向きに

A

\ni

a

と表す。

bがAの要素でないときは、

b

\notin

A

または逆向きに

A

b

と表す。

集合をあらわすとき、主に2種類の方法がある。（例は「10以下の自然数のうち偶数であるもの」の集合を表す。）

（1）　要素を書き並べる方法

（2）　要素の満たす条件を述べる方法

である

たとえば、「10以下の自然数のうち偶数であるもの」の集合を表す場合、（1）　の方法（要素を書き並べる方法）では、

{2, 　4, 　6, 　8, 　10}

となる。

一方、（2）の方法（要素の満たす条件を述べる方法）では、

{ x | x=2n (nは自然数), 2 ≤ x≤ 10 }

{ x | xは2以上10以下の偶数 }

{ 2n | 1 ≤ n≤ 5 (nは自然数) }

{ 2n | nは1以上5以下の自然数 }

などのようになる（何通りかある）。

備考

100以下の自然数の集合 A を、さきほどの（1）「要素を書き並べる方法」の方法で書く場合、

A ＝ {1, 　2, 　3, 　4, ・・・ , 99, 　100}

となる。また、この記法の「・・・」のように、要素の個数がとても多い場合や無数にある場合には、｛｝記号内の要素の途中を「・・・」または「……」、「…」などの点々で省略してよい。

（※ なお、ワープロで「……」などの短い点々を出したい場合、「三点リーダー」で変換すると出る。点が6つあっても「三点リーダー」で出る。

東京書籍の検定教科書で、短いほうの三点リーダーを使っている。啓林館などは、6つの点の長い三点リーダーを使っている。）

100以下の偶数の集合 B は、この記法（要素を書き並べる方法）では、

B ＝ {2,　 4, 　6, ・・・ , 98, 　100}

のようになる。

正の偶数全体の集合の要素は（1）「要素を書き並べる方法」の方法で書く場合、

{2, 　4, 　6, 　・・・}

のようにも書ける。

集合どうし[編集]

部分集合[編集]

2つの集合A,Bがあり、x∈A ならば x∈Bが成り立つとき、AはBの 部分集合 (ぶぶんしゅうごう、英：subset)であるといい、「BはAを含む」か「AはBに含まれる」という。この状態を記号で

A ⊂ B

または

B ⊃ A

で表す。

補足　　

Aの部分集合にはA自身もある。（つまり　A ⊂ A　である）。

また、A,B の集合の要素が同じとき、

A ＝ B

で表す。

例

集合 A ＝ {1, 2, 3} と集合 B ＝ {1, 2 , 3 , 4, 5} があるとき、A は Bの部分集合である。

共通部分と和集合[編集]

2つの集合A,Bがあるときそれらの両方の要素であるものの集合を AとBの 共通部分（きょうつうぶぶん）と呼び、

A ∩ B

と書く。

また、集合A,Bの少なくともどちらか一方には属している要素からなる集合のことを、AとBの和集合（わしゅうごう、英：union）と呼び、

A ∪ B

と書く。

3つの集合の共通部分と和集合[編集]

3つの集合 A, B, C については、3つのどれにも属する要素全体の集合を A,B,C の共通部分と呼び、
A ∩ B ∩ C で表す。

また、集合 A, B, C の少なくとも1つに属する要素の集合を A,B,C の和集合と呼び、
A ∪ B ∪ C で表す。

空集合[編集]

たとえば、「10以下の自然数のうちの偶数」の集合Aと、「10以下の自然数のうちの奇数」の集合Bについて、集合Aと集合Bの共通部分には、何も要素が無い。

この例のように、「要素がなにもない」という場合もあるので、数学では「要素がなにもない」場合もひとつの集合として考える。

要素をもたない集合のことを 空集合(くうしゅうごう、英：empty set あるいは null set)といい、記号は

\varnothing

であらわす。

ギリシャ文字のファイ（φ, $\phi \$ ）で表されることが多くあるが、厳密にはそれは誤りである。上の記号の他に $\emptyset$ 等も用いられるが、この教科書では、 $\varnothing$ を用いる。

補足

どのような集合Aにも、空集合は部分集合として含まれる。

つまり、空集合でないある集合をAとすると、

\varnothing

⊂ A

である。

例

集合 { 1, 2 } の部分集合をすべて列挙すると、次の4つの集合になる。

∅ ,　{1} ,　{2} ,　{1,2}

全体集合・補集合[編集]

集合 U を1つ設定し、その集合の要素や部分集合のみを考える場合を考える。このようなとき、集合Uを 全体集合（ぜんたいしゅうごう、英：universal set）という。

全体集合Uの要素のうち、集合Aに属さないもの全体からなる集合のことをAの 補集合 （ほしゅうごう、英：complement）といい、記号で補集合は ${\overline {A}}$ と表す。

すなわち

{\overline {A}}

＝ {x | x∈U かつ x

\notin

A}

である。

{\overline {({\overline {A}})}}

は

{\overline {A}}

の補集合を表す。　　

{\overline {({\overline {A}})}}

は

{\overline {\overline {A}}}

と書く場合もある。

補集合について、次のことが成り立つ。

A∩A＝∅  , 　　A∪A＝U , 　　 ${\overline {({\overline {A}})}}$  ＝A

ド・モルガンの法則^[1]

{\overline {A\cap B}}={\overline {A}}\cup {\overline {B}}

{\overline {A\cup B}}={\overline {A}}\cap {\overline {B}}

下の図を用いて上の法則が正しい事を確かめよう。

2つの集合の一部に重なっている部分がある場合
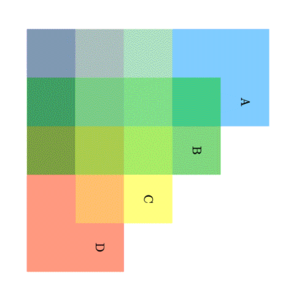
片方がもう片方の部分集合である場合（AとB）と、集合同士が独立している場合（AとC）

3つある場合（AとB、BとC、CとA）
4つある場合（AとB、AとC、AとD、BとC、BとD、CとD）

問題

A={x|xは1以上20以下の2の倍数}・B={y|yは1以上20以下の3の倍数}とする時、以下に適する集合の要素を列挙せよ。ただし、全体集合U={z|zは1以上20以下の整数}とする。

${\overline {A}}$
${\overline {B}}$
$A\cap B$
$A\cup B$
$A\cup {\overline {B}}$
${\overline {A\cap B}}$
${\overline {A}}\cup {\overline {B}}$
$A\cap {\overline {A}}$
$B\cup {\overline {B}}$
$A\cap \varnothing$
$B\cup \varnothing$
$A\setminus B$
$B\setminus A$
$(A\setminus B)\cap (B\setminus A)$

解答

${\overline {A}}$ ={1,3,5,7,9,11,13,15,17,19}
${\overline {B}}$ ={1,2,4,5,7,8,10,11,13,14,16,17,19,20}
$A\cap B$ ={6,12,18}
$A\cup B$ ={2,3,4,6,8,9,10,12,14,15,16,18,20}
$A\cup {\overline {B}}$ ={1,2,4,5,6,7,8,10,11,12,13,14,16,17,18,19,20}
${\overline {A\cap B}}$ ={1,2,3,4,5,7,8,9,10,11,13,14,15,16,17,19,20}
${\overline {A}}\cup {\overline {B}}$ ={1,2,3,4,5,7,8,9,10,11,13,14,15,16,17,19,20}
$A\cap {\overline {A}}=\varnothing$
$B\cup {\overline {B}}=U$ ={1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20}
$A\cap \varnothing =\varnothing$
$B\cup \varnothing$ = {3,6,9,12,15,18}
$A\setminus B$ ={2,4,8,10,14,16,20}
$B\setminus A$ ={3,9,15}
$(A\setminus B)\cap (B\setminus A)=\varnothing$

命題と証明[編集]

命題と条件[編集]

（数学的に）正しいかどうかを明確に判断できる主張を命題（めいだい、英: proposition）と呼ぶ。例えば、「7は素数である」は命題の例である。（一方、「5000は大きい数である」などは命題とはならない。なぜなら「大きい」という言葉の判断が主観的なものであり、判断に明確な基準が設定できないからである。）

ある命題が明確に正しい（と証明される）とき、その命題は真（しん、英：truth）であると呼ぶ。(たとえば、命題「7は素数である」は真である。) 命題が真でないとき、命題は偽（ぎ、英：false）であると言う。たとえば、命題「もし $x^{2}=4$ であれば $x=2$ である。」は、偽の命題である。この方程式は $x=-2$ も解に持つ。

上の命題「" $x^{2}=4$ ならば $x=2$ である"」は $x=-2$ もあてはまるので偽になった。命題 ${\rm {p\Rightarrow q}}$ が偽であるときは、 $p$ は満たすが $q$ を満たさない例が存在する。そのような例を反例（はんれい）という。命題が偽であることを示すには、反例を1つあげればよい。

命題は、「pならばqである」の形式で書かれる場合が多い。

「 pならばqである」という命題を、記号「 $\Rightarrow$ 」を用いて

{\rm {p\Rightarrow q}}

と書く。

また、この条件pをこの命題の仮定（かてい、英：assumption）といい、条件qをこの命題の結論（けつろん）と呼ぶ。

問題

次の命題の真偽を判定し、偽の場合は反例も挙げよ。

　 $ab>0$ ならば $a>0$ かつ $b>0$ である。
　 $a\geq b$ かつ $b\geq a$ ならば $a=b$ である。
　正三角形を2つ用意すればそれらは相似である。
　素数ならば奇数である。

解答

　偽(反例： $a=-1,b=-2$ など)
　真
　真
　偽(反例：2)

命題と集合[編集]

条件や条件を含む命題を考えることは、集合を考えることと同じである。

たとえば、実数 x について「x＞3 ならば x＞1 である」という命題は真である。

ここで「x＞3 である」という条件を p とし、また、x＞3 である数の集合を P としよう。つまり P＝｛x| x>3 ｝である。

同様に、「x＞1である」という条件を q とし、x＞1である数の集合を Q としよう。つまり Q＝｛x| x>1 ｝である。

このとき、命題 ${\rm {p\Longrightarrow q}}$ は真であるが、これは集合の包含関係 P⊂Q が成り立つことに対応している。

必要条件と十分条件[編集]

2つの条件 p,q について、命題「p⇒q」が真であるとき、

pはqであるための 十分条件 （じゅうぶんじょうけん）である

qはpであるための 必要条件 （ひつようじょうけん）である

という。

2つの条件 p.q について、

命題「p⇒q」と命題「q⇒p」の両方とも真であるとき、これを

{\rm {p\Longleftrightarrow q}}

と書き、

pはqであるための必要十分条件である

という。

このとき、pとqを入れ替えることで、

qはpであるための必要十分条件である

ともいえることがわかる。

${\rm {p\Longleftrightarrow q}}$ であるとき、pとqは「同値（どうち）である」という。

「かつ」「または」と否定[編集]

条件 p,q を満たすものの集合をそれぞれ P,Q とする。

このとき、条件「pかつq」および「pまたはq」をあらわす図は、それぞれ右図のようになる。

※ 数学における「または」の使い方では、「pまたはq」は、条件pと条件qの少なくともどちらか一方でも成り立っていればいい。

条件pに対し「pでない」の形の条件を pの否定（ひてい、英：negation）といい、記号は ${\overline {p}}$ で表す。

（※ 高校では習わないが、否定の意味として、 $\lnot {p}$ という記号「¬」もある。）

条件を考えることは集合を考えることと同じなので、集合におけるド・モルガンの法則と同様に、条件においても、ド・モルガンの法則がなり立つ。

ド・モルガンの法則

p かつ q  $\Longleftrightarrow$    p  または  q 

p または q   $\Longleftrightarrow$    p  かつ  q

逆・裏・対偶[編集]

命題「 ${\rm {p\Longrightarrow q}}$ 」に対して

命題「

{\rm {q\Longrightarrow p}}

」を命題「

{\rm {p\Longrightarrow q}}

」の逆（ぎゃく、英：converse）

命題「

{\rm {{\overline {p}}\Longrightarrow {\overline {q}}}}

」を命題「

{\rm {p\Longrightarrow q}}

」の裏（うら、英：inverse）

命題「

{\rm {{\overline {q}}\Longrightarrow {\overline {p}}}}

」を命題「

{\rm {p\Longrightarrow q}}

」の対偶（たいぐう、英：contraposition）

と呼ぶ。

これらは、たがいに右図のような関係にある。

たとえば、もとの命題を

「

x=3\Longrightarrow x^{2}=9

」

だとすると、

裏は「

x\neq 3\Longrightarrow x^{2}\neq 9

」であり

逆は「

x^{2}=9\Longrightarrow x=3

」であり

対偶は「

x^{2}\neq 9\Longrightarrow x\neq 3

」である。

この命題の場合、もとの命題と対偶は、ともに真である。

いっぽう逆については x ＝ -3 という反例があるので、この命題の場合、逆は正しくない。また、裏も同様に、正しくない。

このような例から、次のことが分かる。

ある命題が真であっても、その命題の逆は、かならずしも真とは限らない。
また、ある命題が真であっても、その命題の裏は、かならずしも真とは限らない。

では、もとの命題と対偶との関係は、どうなるだろうか。

この考察をするため、条件pを満たすものを集合Pに対応させ、同様に条件qを満たすものを集合Qに対応させてみよう。

右の集合の図は、p⇒qが真であることを表す図である。この図では、Pに属している要素は、Qにも属している。（つまり ${\rm {P\subset Q}}$ である。）一方、Qに属していいない要素は、Pにも属していない。（つまり ${\rm {{\overline {Q}}\subset {\overline {P}}}}$ である。）このことからから分かるように、

ある命題が真であるとき、その命題の対偶も真となる。
ある命題が偽であるとき、その対偶も偽である。

つまり、一般の命題において、もとの命題と対偶との真偽は一致する。

背理法[編集]

ある命題の結論を否定して、その否定のもとで矛盾が起こることを述べることで、その命題が真であることを導出する仕方を背理法（はいりほう、英: proof by contradiction など）と呼ぶ。

たとえば、「Aではないことを証明せよ」という問題を解く時は「Aであると仮定する」と書き出して、仮定したことと矛盾する部分を作って「矛盾するのでAではない。」と証明を終える。

例題

素数は無限に存在する。

証明

素数が有限個であったと仮定する。すべての素数の積を $a$ とすると、 $a+1$ はどの素数で割っても1余ることになり、1以外の自然数であって、素数の積に分解できないものが存在することになる。 $a+1$ の約数のうち1以外で最も小さいものを $b$ とすると、 $b$ は1と $b$ 以外の約数を持たない。したがって $b$ が素数であることになるが、 $a+1$ がどの素数でも割り切れないことと矛盾する。したがって、素数は有限個ではない。■

背理法と日常的な思考

背理法は多くの高校生が苦手としています。「Aである」ことを証明するために、わざわざ「Aでない」と仮定して矛盾を導くという論理の展開が不自然に感じられ、それが苦手意識につながっているようです。しかし、背理法の発想は私たちの日常的な思考でもよく使われています。ここでは、その例をいくつか紹介しましょう。

一つ目はアリバイ証明です。もしあなたが事件の犯人であると疑われたとします。そのとき、「自分が犯人ではない」ということをどのように証明しますか。ただ「自分は犯人ではない」と言うだけでは説得力がありません。この場合、犯行現場がA駅であったが、「自分は事件が起きたときにはB駅にいた」ことを証明できる、つまりアリバイが成り立つならば自分が犯人ではないという有力な証拠となります。この仕組みを簡単な文にすると以下のようになります。

私が犯人だと仮定すると、A駅にいたことになる。

しかし私はB駅にいた（＝A駅にいなかった）。

私が同じ時間にA駅とB駅の両方にいることはできないので、当初の仮定と矛盾する。

ゆえに私が犯人だという仮定がまちがっていたので、私は犯人ではない。

アリバイを示すことで自分の無実を証明するというのは、実はこういう仕組みになっているのです。なお、アリバイを示して無実を証明する方法には、やはり高校生の多くが苦手とする対偶証明法を使う方法もあります。そちらはみなさんで考えてみてください。

二つ目は消去法での選択肢の選び方です。たとえば、平成30年度「倫理」のセンター試験の大問1問7（マークシート番号7）の問題を見てみましょう。（バグと思わしき現象が起きたためリンクは貼りません。お手数ですが、各自確認して下さい。）　この正解を導き出すのに背理法の文章を利用してみましょう。

1が正解だと仮定すると、1の選択肢はグラフを正しく説明している。

しかし、2015年のトップ3（日伊独）と2050年のトップ3（日伊韓）は異なるので、正しい説明になっておらず、仮定と矛盾する。

ゆえに1を正解とした仮定は誤っていた。

だから、1の選択肢は正しくないので消す。

これを繰り返すと、誤った選択肢を消去して正解を導くことができますね（「倫理」の知識は全くいらないので、皆さんも挑戦してみてください）。

もちろん、アリバイ証明にしても消去法にしても、いつもこうした操作で解いているわけではありません。むしろ、背理法のことは意識しないで解くのが当たり前でしょう。実は背理法の考え方は本来、何気なく実行できるくらい自然な発想なのです。ほかにも、皆さんの日常的な考え方の中に背理法の形にそうものがあるはずです。逆に一見正しい背理法に見えても、実はインチキな論理展開のものもあるでしょう。そうしたことを探していくのも論理的に考えるためのトレーニングになります。ぜひ、挑戦してみてください。

【参考文献】

『論理的に考えること』（山下正男著, 岩波書店（岩波ジュニア新書））
『論理的に考え、書く力』（吉沢光雄著, 光文社（光文社新書））

脚注[編集]

^
ド・モルガン

w:オーガスタス・ド・モルガンは19世紀イギリスの数学者。

[1] 
ド・モルガン

w:オーガスタス・ド・モルガンは19世紀イギリスの数学者。

[1]

旧課程(-2012年度)高等学校数学A/集合と論理

目次

集合と論理[編集]

集合とは[編集]

集合や要素の関係の表し方[編集]

集合と要素[編集]

集合どうし[編集]

部分集合[編集]

共通部分と和集合[編集]

3つの集合の共通部分と和集合[編集]

空集合[編集]

全体集合・補集合[編集]

命題と証明[編集]

命題と条件[編集]

命題と集合[編集]

必要条件と十分条件[編集]

「かつ」「または」と否定[編集]

逆・裏・対偶[編集]

背理法[編集]

脚注[編集]

案内メニュー