線型代数学/行列概論

行列

定義

$m$と$n$を自然数とする。$mn$個の数$a_{11},a_{21},\cdots ,a_{m1},\cdots ,a_{mn}$を、括弧で囲んだ中に次のように縦に$m$個、横に$n$個、表のように並べて書いたものを、$m$行$n$列の行列(matrix)と言う。(m×n)-行列とも言う。

$A={\begin{pmatrix}a_{11}&a_{12}&a_{13}&\dots &a_{1n}\\a_{21}&a_{22}&a_{23}&\dots &a_{2n}\\a_{31}&a_{32}&a_{33}&\dots &a_{3n}\\\vdots &\vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&a_{m3}&\dots &a_{mn}\\\end{pmatrix}}$

この行列を構成する$a_{ij}$を行列の成分(element)と言う。横に並んだ一列を行(row)、縦に並んだ一列を列(column)と言う。上から$i$番目の行を第$i$行といい、左から$j$番目の列を第$j$列と言う。行列内の第$i$行、第$j$列に位置する成分を、この行列の$(i,j)$-成分と言う。行列Aの$(i,j)$成分が、$a_{ij}$である行列$A$を$A=(a_{ij})$と書く。

行列の第k列の列ベクトルを$\mathbf {a} _{k}={\begin{pmatrix}a_{1k}\\a_{2k}\\\vdots \\a_{mk}\end{pmatrix}}$とする。 行列は、この列ベクトルを用いて、行列は、$A=(\mathbf {a} _{1},\mathbf {a} _{2},\cdots ,\mathbf {a} _{n})$と表すこともできる。 同じように、行列の第k行の行ベクトルを$\mathbf {a} _{k}=(a_{k1},a_{k2},\cdots ,a_{km})$としたとき。 行列は、この行ベクトルを用いて、行列は、$A={\begin{pmatrix}\mathbf {a} _{1}\\\mathbf {a} _{2}\\\vdots \\\mathbf {a} _{n}\end{pmatrix}}$と表すこともできる。

成分が全て実数の行列を実行列と言い、成分が全て複素数の行列を複素行列という。また、$m=n$の場合、(n×n)-行列を特にn次正方行列と呼ぶ。

相等関係

2つの(m×n)-行列$A,B$に関し、$A$と$B$が等しいとは、2つの行列の対応する成分が全て等しいことを言う。すなわち、

$A=(a_{ij}),B=(b_{ij})$のとき、

$A=B\iff \forall i,j,a_{ij}=b_{ij}$

加法

2個のm行n列行列$A$と$B$について、行列の和 A+B を次のように定義する。 $A={\begin{pmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\\\end{pmatrix}}$, $B={\begin{pmatrix}b_{11}&b_{12}&\cdots &b_{1n}\\b_{21}&b_{22}&\cdots &b_{2n}\\\vdots &\vdots &\ddots &\vdots \\b_{m1}&b_{m2}&\cdots &b_{mn}\\\end{pmatrix}}$ のとき、

$A+B={\begin{pmatrix}a_{11}+b_{11}&a_{12}+b_{12}&\cdots &a_{1n}+b_{1n}\\a_{21}+b_{21}&a_{22}+b_{22}&\cdots &a_{2n}+b_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}+b_{m1}&a_{m2}+b_{m2}&\cdots &a_{mn}+b_{mn}\\\end{pmatrix}}$

$A=(a_{ij}),B=(b_{ij})$のとき、$A+B=(a_{ij}+b_{ij})$と表現することもできる。

スカラー乗法

また、行列$A$と定数$\lambda$について、行列の定数倍 $\lambda A$ を次のように定義する。 $A={\begin{pmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\\\end{pmatrix}}$ のとき、

$\lambda A={\begin{pmatrix}\lambda a_{11}&\lambda a_{12}&\cdots &\lambda a_{1n}\\\lambda a_{21}&\lambda a_{22}&\cdots &\lambda a_{2n}\\\vdots &\vdots &\ddots &\vdots \\\lambda a_{m1}&\lambda a_{m2}&\cdots &\lambda a_{mn}\\\end{pmatrix}}$

特に、$\lambda =-1$のとき、$(-1)A$を$-A$と書く。

また、$A+(-B)$を$A-B$と書く。

積

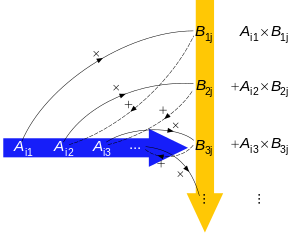行列の積の計算過程の図示。行列Aの第i 行と行列Bの第j 列の各成分の積を実線部分のように取り、続いて点線のように加えていくことにより、積ABのij成分を得る。

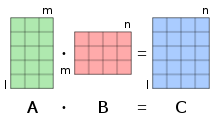行列の積では、行列Aの列数と行列Bの行数が同じでなくてはいけない。行列Cの行数は行列Aの行数であり、行列Cの列数は行列Bの列数である。

２個の行列$A$と$B$について、Aの列数とBの行数が同じで$A,B$の場合に、行列の積$AB$を次のように定義する。 $A={\begin{pmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\\\end{pmatrix}}$ , $B={\begin{pmatrix}b_{11}&b_{12}&\cdots &b_{1l}\\b_{21}&b_{22}&\cdots &b_{2l}\\\vdots &\vdots &\ddots &\vdots \\b_{n1}&b_{n2}&\cdots &b_{nl}\\\end{pmatrix}}$ のとき、AとBの積ABを

$c_{ij}=\sum _{k=1}^{n}a_{ik}b_{kj}=a_{i1}b_{1j}+a_{i2}b_{2j}+\cdots +a_{in}b_{nj}~(i=1,\cdots ,m,~j=1,\cdots ,l)$ によって

$AB={\begin{pmatrix}c_{11}&c_{12}&\cdots &c_{1l}\\c_{21}&c_{22}&\cdots &c_{2l}\\\vdots &\vdots &\ddots &\vdots \\c_{m1}&c_{m2}&\cdots &c_{ml}\\\end{pmatrix}}$

と定める。 この定義は難しく見えるが、行列$A$の$i$行目の行ベクトルと、行列$B$の$j$列目の列ベクトルの内積が行列$AB$の$(i,j)$成分になっているだけである。

行列同士の積は全ての二行列に対して定義されているわけではない。(m×n)-行列と(n×l)-行列の間にのみ定義されているのである。

例題 次の計算をせよ。

${\begin{pmatrix}-7&-6&-5\\-4&-3&-2\\\end{pmatrix}}{\begin{pmatrix}-1&0&1\\2&3&4\\5&6&7\\\end{pmatrix}}$

解答

${\begin{aligned}{\begin{pmatrix}-7&-6&-5\\-4&-3&-2\\\end{pmatrix}}{\begin{pmatrix}-1&0&1\\2&3&4\\5&6&7\\\end{pmatrix}}&={\begin{pmatrix}(-7)(-1)+(-6)\times 2+(-5)\times 5&(-7)\times 0+(-6)\times 3+(-5)\times 6&(-7)\times 1+(-6)\times 4+(-5)\times 7\\(-4)(-1)+(-3)\times 2+(-2)\times 5&(-4)\times 0+(-3)\times 3+(-2)\times 6&(-4)\times 1+(-3)\times 4+(-2)\times 7\\\end{pmatrix}}\\&={\begin{pmatrix}-30&-48&-66\\-12&-21&-30\\\end{pmatrix}}\end{aligned}}$

例題

$m\times n$ 行列 $A$、$n\times p$ 行列 $B$、$p\times q$ 行列 $C$ について、 $A(BC)=(AB)C$ を証明せよ。

解答

ここでは、行列 $X$ の $(i,j)$ 成分を $[X]_{ij}$ と表すことにする。

${\begin{aligned}{[A(BC)]_{ij}}&=\sum _{k=1}^{n}[A]_{ik}[BC]_{kj}\\&=\sum _{k=1}^{n}\left([A]_{ik}\sum _{l=1}^{p}[B]_{kl}[C]_{lj}\right)\\&=\sum _{k=1}^{n}\sum _{l=1}^{p}[A]_{ik}[B]_{kl}[C]_{lj}\\&=\sum _{l=1}^{p}\left([C]_{lj}\sum _{k=1}^{n}[A]_{ik}[B]_{kl}\right)\\&=\sum _{l=1}^{p}[AB]_{il}[C]_{lj}\\&=[(AB)C]_{ij}\end{aligned}}$

よって、$(AB)C=A(BC)$

零行列

行列成分が全て0の行列を零行列（zero matrix）といい、$0$と書く。特に(m×n)-行列であることを明示する場合には、0_m,nと書き、n次正方行列であることを明示する場合には0_nと書く。 任意の行列に、適当な零行列をかけると、常に零行列が得られる。零行列は、実数における0に似ている。

単位行列

$A=(a_{ij})$ に対して、成分$a_{kk},~k=1,\cdots ,n$を、$n$次正方行列$A$の対角成分（diagonal element）という。

行列の対角成分がすべて1で、その他の成分がすべて0であるような正方行列 $I={\begin{pmatrix}1&0&\cdots &0\\0&1&\cdots &0\\\vdots &\vdots &\ddots &\vdots \\0&0&\cdots &1\end{pmatrix}}$を単位行列（elementary　matrix、あるいはidentity matrix）といい、$E_{n}$や$I_{n}$と表す。$n$が明らかである場合にはしばしば省略して、$E$や$I$と表すこともある。クロネッカーのデルタを使うと$I=(\delta _{ij})$.

行列の演算の性質

$A,B,C$を任意の$(m,n)$行列 、$\lambda ,\mu$を任意の定数、$0$を零行列、$I$を単位行列とすると、以下の関係が成り立つ。

1. 結合法則: $(A+B)+C=A+(B+C)$
2. 交換法則: $A+B=B+A$
3. $\lambda (A+B)=\lambda A+\lambda B$
4. $(\lambda +\mu )A=\lambda A+\mu A$
5. $(\lambda \mu )A=\lambda (\mu A)$
6. $1A=A$
7. $0A=0$
8. $A+0=A$
9. $A-A=O$
10. $A(B+C)=AB+AC$
11. $(A+B)C=AC+BC$
12. $A0=0A=0$
13. $AI=IA=A$

転置行列

$A={\begin{pmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\end{pmatrix}}$ に対して

$A^{\mathsf {T}}={\begin{pmatrix}a_{11}&a_{21}&\cdots &a_{m1}\\a_{12}&a_{22}&\cdots &a_{m2}\\\vdots &\vdots &\ddots &\vdots \\a_{1n}&a_{2n}&\cdots &a_{mn}\\\end{pmatrix}}$

を$A$の転置行列（transposed matrix）と言い、$A^{\mathsf {T}}$や$^{t}A$と表す。

つまり$A^{\mathsf {T}}$とは、$A$の縦横をひっくり返した行列である。

以下のような性質が成り立つ。

1. $(A^{\mathsf {T}})^{\mathsf {T}}=A$
2. $(A+B)^{\mathsf {T}}=A^{\mathsf {T}}+B^{\mathsf {T}}$
3. $(\lambda A)^{\mathsf {T}}=\lambda (A^{\mathsf {T}})$
4. $(AB)^{\mathsf {T}}=B^{\mathsf {T}}A^{\mathsf {T}}$

証明

$A=(a_{ij}),B=(b_{ij})$とする。

1. 転置行列とは、行と列を入れ替えた行列なので、2回行と列を入れ替えれば、もとの行列に戻る。
2. $(A+B)^{\mathsf {T}}$の$(i,j)$成分は$a_{ji}+b_{ji}$であり、$A^{\mathsf {T}}+B^{\mathsf {T}}$の$(i,j)$成分は$a_{ji}+b_{ji}$である。
3. $(\lambda A)^{\mathsf {T}}$の$(i,j)$成分は$\lambda a_{ji}$であり、$\lambda (A^{\mathsf {T}})$の$(i,j)$成分は$\lambda a_{ji}$であるから。
4. $AB$の$(i,j)$成分は$=\sum _{k=1}^{n}a_{ik}b_{kj}$なので、$(AB)^{\mathsf {T}}$の$(i,j)$成分は$\sum _{k=1}^{n}a_{jk}b_{ki}$である。次に、$A^{\mathsf {T}}$の$(i,j)$成分は$a_{ji},B^{\mathsf {T}}$の$(i,j)$成分は$b_{ji}$であるので、$A^{\mathsf {T}}B^{\mathsf {T}}$の$(i,j)$成分は$\sum _{k=1}^{n}a_{jk}b_{ki}$であるから。

ただし、$n$を$A$の列数とする。

複素行列

ある行列Aのすべての成分の複素共役を取った行列${\overline {A}}={\begin{pmatrix}{\overline {a}}_{1,1}&\cdots &{\overline {a}}_{1,m}\\\vdots &\ddots &\vdots \\{\overline {a}}_{n,1}&\cdots &{\overline {a}}_{m,n}\end{pmatrix}}$ を、複素共役行列（complex conjugate matrix）という。

以下のような性質がある。

• ${\overline {\overline {A}}}=A$
• ${\overline {A+B}}={\overline {A}}+{\overline {B}}$
• ${\overline {\lambda A}}={\overline {\lambda }}~{\overline {A}}$
• ${\overline {AC}}={\overline {C}}~{\overline {A}}$

一番最後の式には注意せよ。とりあえず、ここで一休みして、演習をやろう。

演習

1.定理(1.5.1)を証明せよ

2.計算せよ

(1)${\begin{pmatrix}1&-2&3\\2&1&0\\\end{pmatrix}}{\begin{pmatrix}-2&-1&1\\1&2&-3\\2&0&3\\\end{pmatrix}}$

(2)${\begin{pmatrix}1&1&1\\1&1&1\\1&1&1\\\end{pmatrix}}{\begin{pmatrix}2\\3\\4\\\end{pmatrix}}$

(3)${\begin{pmatrix}1&i\\-i&1\\\end{pmatrix}}{\begin{pmatrix}1-i&0\\0&1+i\\\end{pmatrix}}$

(4)${\begin{pmatrix}2&1+i&3i\\\end{pmatrix}}{\begin{pmatrix}2\\1+i\\-3i\\\end{pmatrix}}$

($i={\sqrt {-1}}$)

3.

対角成分*¹が全て1それ以外の成分が全て0のn次正方行列*²を、単位行列と言い、E_nと書く。つまり、

$E_{n}=(\delta _{i,j})$, $\delta _{i,j}={\begin{cases}1(i=j)\\0(i\neq j)\end{cases}}$

このδ_i,jを、クロネッカーのデルタ（Kronecker delta）と言う、またはクロネッカーの記号と言う。この時、次のことを示せ。

(1)$A={\begin{pmatrix}-1&-2\\-2&-4\\\end{pmatrix}}$のとき、AX=E₂を満たすXは存在しない

(2)$B={\begin{pmatrix}-1&-2\\0&0\\\end{pmatrix}}$の時、(1)の定義で、BX=AとなるXが存在しない。

また、YB=Aを満たすYが無数に存在する。

(3)n次行列(n次正方行列)Aのある列が全て0なら、AX=Eを満たすXは存在しない。

*¹対角成分:n次正方行列A=(a_i,j)で、(i=1,2,...,n;j=1,2,...,n)a_i,i=a_1,1,a_2,2,...,a_n,nのこと

*²n次正方行列:行と、列の数が同じnの時の行列

区分け

$A={\begin{pmatrix}1&3&-1&0\\2&1&3&2\\1&2&3&4\\\end{pmatrix}}$は、

$A_{1}={\begin{pmatrix}1&3&-1\\2&1&3\\\end{pmatrix}}$,　 $A_{2}={\begin{pmatrix}0\\2\\\end{pmatrix}}$

$A_{3}={\begin{pmatrix}1&2&3\\\end{pmatrix}}$,　 $A_{4}={\begin{pmatrix}4\\\end{pmatrix}}$

とすることで、

$A={\begin{pmatrix}A_{1}&A_{2}\\A_{3}&A_{4}\\\end{pmatrix}}$

一般に、

定義(2.1)行列の区分け

(l,m)型行列A=(a_i,j)をp-1本の横線とq-1本の縦線でp×qの島に分けて、上からs番目、左からt番目の行列をA_s,tとおいて、

$A={\begin{pmatrix}A_{1,1}&A_{1,2}&A_{1,3}&\cdots &A_{1,q}\\A_{2,1}&A_{2,2}&A_{2,3}&\cdots &A_{2,q}\\A_{3,1}&A_{3,2}&A_{3,3}&\cdots &A_{3,q}\\\vdots &\vdots &\vdots &\ddots &\vdots \\A_{p,1}&A_{p,2}&A_{p,3}&\cdots &A_{p,q}\\\end{pmatrix}}$

とすることを、行列の区分けと言う。

定理(2.2)

同様に区画された同じ型の、

$A={\begin{pmatrix}A_{1,1}&A_{1,2}&A_{1,3}&\cdots &A_{1,q}\\A_{2,1}&A_{2,2}&A_{2,3}&\cdots &A_{2,q}\\A_{3,1}&A_{3,2}&A_{3,3}&\cdots &A_{3,q}\\\vdots &\vdots &\vdots &\ddots &\cdots \\A_{p,1}&A_{p,2}&A_{p,3}&\cdots &A_{p,q}\\\end{pmatrix}}$,　 $B={\begin{pmatrix}B_{1,1}&B_{1,2}&B_{1,3}&\cdots &B_{1,r}\\B_{2,1}&B_{2,2}&B_{2,3}&\cdots &B_{2,r}\\B_{3,1}&B_{3,2}&B_{3,3}&\cdots &B_{3,r}\\\vdots &\vdots &\vdots &\ddots &\vdots \\B_{q,1}&B_{q,2}&B_{q,3}&\cdots &B_{q,r}\\\end{pmatrix}}$

$C=AB={\begin{pmatrix}C_{1,1}&C_{1,2}&C_{1,3}&\cdots &C_{1,r}\\C_{2,1}&C_{2,2}&C_{2,3}&\cdots &C_{2,r}\\C_{3,1}&C_{3,2}&C_{3,3}&\cdots &C_{3,r}\\\vdots &\vdots &\vdots &\ddots &\vdots \\C_{p,1}&C_{p,2}&C_{p,3}&\cdots &C_{p,r}\\\end{pmatrix}}$

がある。この時、

$C_{s,u}=\sum _{t=1}^{q}A_{s,t}B_{t,u}=A_{s,1}B_{1,u}+A_{s,2}B_{2,u}+...+A_{s,q}B_{q,u}$　　　　　(2.3)

(s=1,2,...,p;u=1,2,...,r)

(証明)

(i)

A_s,tを(l_s,m_t),B_t,uを(m_t,n_u)とすると、A_s,tB_t,uは、tと関係なく、(l_s,m_t)型行列であるから、それらの和C_s,uも(l_s,m_t)型行列である。よって、(2.3)は意味を成す。

(ii)

Aを(l,m)Bを(m,n)型、(2.3)の両辺の対応する成分を(α,β)、

$i=\sum _{j=1}^{s-1}l_{j}+\alpha =l_{1}+l_{2}+{\dot {+}}l_{s-1}+\alpha$,

$k=\sum _{j=1}^{u-1}n_{j}+\beta =n_{1}+n_{2}+{\dot {+}}n_{u-1}+\beta$.

とおけば、C_s,uの(α,β)成分とCの(i,k)成分,A_s,tB_t,uは等しく、それは

$\sum _{j=1}^{m}a_{i,j}b_{j,k}$であり且

$\sum _{j=(\sum _{j=1}^{t-1}m_{j})+1}^{\sum _{j=1}^{t}m_{t}}a_{i,j}b_{j,k}$

⇔$\sum _{t=1}^{q}A_{s,t}B{t,u}$の(α,β)成分=$\sum _{j=1}^{m}a_{i,j}b_{j,k}$

(i),(ii)より、定理(2.2)は証明された。

例

p=q=r=2とすると、${\begin{pmatrix}A_{1,1}&A_{1,2}\\A_{2,1}&A_{2,2}\\\end{pmatrix}}{\begin{pmatrix}B_{1,1}&B_{1,2}\\B_{2,1}&B_{2,2}\\\end{pmatrix}}={\begin{pmatrix}A_{1,1}B_{1,1}+A_{1,2}B_{2,1}&A_{1,1}B_{1,2}+A_{1,2}B_{2,2}\\A_{2,1}B_{1,1}+A_{2,2}B_{2,1}&A_{2,1}B_{1,2}+A_{2,2}B_{2,2}\\\end{pmatrix}}$　　　　　(2.4)

A_2,1,B_2,1=Oとすると、(2.4)右辺は

${\begin{pmatrix}A_{1,1}B_{1,1}&A_{1,1}B_{1,2}+A_{1,2}B_{2,2}\\O&+A_{2,2}B_{2,2}\\\end{pmatrix}}$

と、区分けはこの時威力を発揮する。A_1,2,B_1,2=Oならさらに威力を発揮する。

${\begin{pmatrix}A_{1,1}B_{1,1}&O\\O&+A_{2,2}B_{2,2}\\\end{pmatrix}}$

例

単位行列E_nをn個の縦ベクトルに分割したときの、そのベクトルをn項単位ベクトルと言う。これは、ベクトルの項でのべた、2,3次における単位ベクトルの定義の一般化である。Eのことを単位行列と言う意味が分かっただろうか。ここでAを、(l,m)型Bを(m,n)型と定義しなおし、

B=(b₁,b₂,...,b_n)

とすると、

AB=(Ab₁,Ab₂,...,Ab_n)

この事実は、定理(2.2)の特殊化である。

縦ベクトルx=(x_i)は、

x=x₁e₁+x₂e₂+...+x_ke_k

と表す事が出来るが、一般に

x₁a₁+x₂a₂+...+x_ka_k

をa₁,a₂,...,a_kの線型結合と言う。

演習

計算せよ

(1)${\begin{pmatrix}1&1&0&0\\0&-2&0&0\\0&0&-2&3\\0&0&1&1\\\end{pmatrix}}{\begin{pmatrix}2&1&0&0\\0&1&0&0\\0&0&1&1\\0&0&-2&3\\\end{pmatrix}}$

(2)${\begin{pmatrix}2i&0&0\\0&-i&0\\0&0&3i\\\end{pmatrix}}{\begin{pmatrix}-1&0&0\\0&2&0\\0&0&1\\\end{pmatrix}}(i={\sqrt {-1}})$

逆行列

$AX=XA=I$となる行列$X$が存在すれば、$X$を$A$の逆行列といい、$A^{-1}$と表す。
また、$A$に逆行列が存在すれば、$A$を正則行列といい、逆行列はただ一通りに決まる。

証明

$A$に逆行列$X,Y$が存在すると仮定すると。

$AX=XA=I,AY=YA=I$が成り立つので、

$X=XI=X(AY)=(XA)Y=IY=Y$よって$X=Y$となるので、逆行列が存在すれば、ただ一通りに決まる。

逆行列については、以下の性質が成り立つ。

1. $(A^{-1})^{-1}=A$
2. $(AB)^{-1}=B^{-1}A^{-1}$

証明

1. $A^{-1}$の逆行列は、定義から、$A^{-1}X=XA^{-1}=I$となる$X$であるが、$X$に$A$を代入すると成り立っているので、$(A^{-1})^{-1}=A$である。
2. $AB$の逆行列は、$(AB)X=X(AB)=I$となる$X$であるが、$X$に$B^{-1}A^{-1}$を代入すると、

$(AB)(B^{-1}A^{-1})=AIA^{-1}=AA^{-1}=I$

$(B^{-1}A^{-1})(AB)=B^{-1}IB=B^{-1}B=I$

となり、式が成り立っているので$(AB)^{-1}=B^{-1}A^{-1}$である。

定義(3.2.4)対称区分け

　正方行列を一辺が等しい正方形の島に区分けするとき、この区分けを対称区分けと言う。

簡単な証明で

「定理(3.2.5)

対称区分けで、

$A={\begin{pmatrix}A_{1,1}&A_{1,2}\\O&A_{2,2}\\\end{pmatrix}}$

において、A_1,1とA_2,2が正則ならば、Aも正則である。」

及び次のことが言える。

「対称区分けで、

A=(A_i,j)で、(i,j=1,2,...n)$A_{i,j}={\begin{cases}A_{i}(i=j)\\O\end{cases}}$ならば、Aが正則である必要十分条件は、A_iがすべて正則である事である」

その逆行列は、次のように与えられる。

$A^{-1}={\begin{cases}A_{i}^{-1}(i=j)\\O\end{cases}}$

また、(3.2.5)の逆行列A_-1は、

$A^{-1}={\begin{pmatrix}A_{1,1}^{-1}&-A_{1,1}^{-1}A_{1,2}A_{2,2}^{-1}\\O&A_{2,2}^{-1}\end{pmatrix}}$である。

行列の累乗

行列の累乗は、$A$を正則行列、$n$を自然数とし、次のように定義される。

$A^{n}=\underbrace {AA...A} _{n}$

$A^{0}=I$

$A^{-n}=\underbrace {A^{-1}A^{-1}...A^{-1}} _{n}$

行列の累乗には以下の性質がある。

$A^{k}A^{l}=A^{k+l}$

$(A^{k})^{l}=A^{kl}$

$AB=BA$のとき$(AB)^{k}=A^{k}B^{k}$ ただし:$A$を正則行列、$k,l$を自然数とする。

証明
$(AB)^{k}=ABABAB\cdots ABAB$

$AB=BA$なので、隣り合うAとBを入れ替えていくと

$ABABAB\cdots ABAB=AABABA\cdots BABB$
これを続けると、$\underbrace {AA\cdots A} _{k}\underbrace {BB\cdots B} _{k}$となる。

その他

正方行列(a_i,j)において、a_i,iを対角成分と言う。また、対角成分以外が全て0である正方行列のことを対角行列（diagonal matrix）と言う。対角行列が正則であるための、必要十分条件は、対角成分が全て0でないということである。4章で示される。対角行列の中でも更にスカラー行列と呼ばれるものがある。それはcE(c≠0)の事である。勿論Eはc=1の時のスカラー行列で、対角行列である。また、スカラー行列cEを任意行列Aに掛けると、CAとでる。対角行列が定義されたので、固有和が定義できる。

定義(3.2.6)固有和または跡（trace）

正方行列Aの固有和

TrA

とは、対角成分の総和である。

次のような性質がある

Tr(cA)=cTrA,　Tr(A+B)=TrA+TrB, Tr(AB)=Tr(BA)