中等教育前期の数学/幾何編/下巻/線分の比と計量

平面図形

ここでは、三角形の重心、外心、内心などについて説明する。更に、四角形が円に内接する条件や方べきの定理などについても扱う。

三角形の性質

三角形の重心

三角形の頂点から相対する辺の中点に対して下ろした線分のことを 中線 （ちゅうせん）という。

三角形の3つの中線の交点のことを、その三角形の 重心 （じゅうしん）という。

右図では、点Gが△ABCの重心である。

三角形の重心

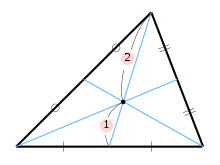
三角形の重心 定理 三角形の3本の中線は1点で交わる。また、その交点は中線を 2:1 に内分する。

• 証明

△ ABC を取りBC,ACの中点をそれぞれ D, E とする。また、線分AD,BEの交点を G とする。ここで、点Eから線分ADに向かって辺BCに平行な線分を取り、 線分ADとの交点を L とする。

このとき、三角形 GEL と、GBDは相似であり 互いの相似比は 1:2 であることを示す。 LEとBCが平行であることから、

$\angle GBD=\angle GEL$

$\angle GDB=\angle GLE$

となり、2角が等しいことから△ GEL と △ GBD は相似である。 更に、LEとBCが平行であることから△ALEと△ADCも相似であり、その相似比は点Eが線分ACの中点であることを考えると、1:2である。よって、

$LE:DC=1:2$

が成立し、△GELと△GBDの相似比は1:2であることがわかった。 また、△ALEと△ADCの相似から

$AL=LD$

が得られる。これらのことからAGとADの比を計算すると、

$AG=AL+LG={\frac {1}{2}}AD+{\frac {1}{3}}LD$

$={\frac {1}{2}}AD+{\frac {1}{6}}AD={\frac {2}{3}}AD$

となり、確かに G はADを2:1に内分する点になっている。

同様にして、頂点Cから線分ABにむかって中線AKを引き、中線AKとADとの交点をHとすると、 上記の証明と同様の論理でADは点Hにより 2:1 に内分される。

内分の比率が同じなので、点Hと点Gは一致する。

（※ 高校数学の範囲外）「重心」の力学的なバランス

※ 2019年現在では高校の理科で 重心 の力学的な習うが、過去のカリキュラムでは中学の数学で後述の話題を扱ってた時代がある。

厚めの画用紙などで三角形をつくり、その三角形を水平にして、右図のように三角形の重心の部分で、棒で支えると、

水平方向の重さのバランスがとれるので、三角形を水平に保つことができる。

そもそも、このように重さのバランスを取れる場所であるので「重心」という名前がついている。重心の英語の center of gravity という英単語も、「重力の中心」という意味である。

理科の「物理」科目で習う「重心」とは、この例のように、重さのバランスを取れる部分という意味である。

なお、このような力学的な「重心」については、三角形だけでなく四角形や五角形などでも、同様に水平方向の重さのつりあいをとれる点として、力学的に「重心」を定義できる。

また、平面図形だけでなく立体図形でも同様、力学的に「重心」を定義できる。

三角形の外心

※ 検定教科書では、辺の両端の2つの頂点から等距離にある点を結んだ線分が垂直二等分線である事は、証明の不要な事実として扱っている。この性質を利用して、下記の定理が証明される。

三角形の外心

定理 三角形の3つの辺の垂直二等分線は1点で交わる。

証明

△ABCを取り、辺AB,AC のそれぞれに対して垂直二等分線を取り、2直線の交点をOとする。このとき、点OがAB,ACのそれぞれに対する垂直2等分線上にあることから

$AO=OB$ 　かつ　 $AO=OC$

であるので、

$OB=OC$

が成り立つ。

よって点Oは辺BCの垂直二等分線上にある。　　（証明 おわり）

上の証明から、$OA=OB=OC$ であるので、この点は三角形の3つの頂点から等距離にあることが分かるので、この点Oを中心として円を書くと、三角形ABCの頂点3つを通る円を書くことができる。

このように、三角形の3つの頂点を通る円（右図では赤線の部分）のことを外接円(がいせつえん、 英：circumscribed circle)という。

そして、外接円の中心（右図の点Oの部分）のことを、その三角形の 外心（がいしん）という。

三角形の内心

三角形の内心

三角形の3角のそれぞれに対して角の2等分線を取ったとき、それぞれの直線は1点で交わる。

• 証明

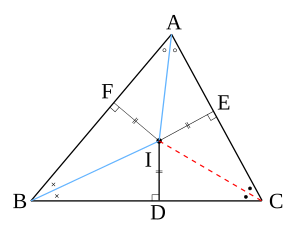
△ABCを取り、角A,Bについて角の2等分線を取り2直線の交点をIと呼ぶ。 さらに、点Iから辺BC,CA,ABに下ろした垂線とそれぞれの辺の交点をそれぞれ D,E,F と呼ぶとする。このとき、角Aの二等分線の性質から

$IE=IF$

が成り立ち、同様に角Bの2等分線の性質から

$IF=ID$

が成り立つので、

よって

$ID=IE$

である。

したがって、点Iは角Cの二等分線上にある。（証明 おわり）

ID＝IE＝IF なので、図のように三角形の三辺に接する円を書くことができ。この円を △ABCの内接円 （ないせつえん、英：inscribed circle）といい、その中心Iを内心（ないしん）という。

• 研究

なお、三角形の内接円の半径をrとすると、面積Sと三辺の長さa,b,cとの間に

$S={\frac {1}{2}}r(a+b+c)$

の関係式が成り立つ（△ABI、△BCI、△CAIの3つの三角形の面積を考えてみよ）。面積Sはヘロンの公式を用いれば三辺の長さから計算できるので、結局三辺の長さがわかっていれば内接円の半径は計算できることがわかる。

三角形の垂心

外心の性質を利用して、次の定理が証明できる。

三角形の垂心

定理 三角形の各頂点から対辺またはその延長に降ろした垂線は、1点で交わる。

証明

点Aを通り辺BCに平行な直線、点Bを通り辺CAに平行な直線、点Cを通り辺ABに平行な直線をかき、これらの直線の交点を図のようにP,Q,Rとする。

すると、四角形RBCA は平行四辺形なので、 RA ＝ BC である。 同様に、四角形ABCQ も平行四辺形なので BC＝AQ である。 よって RA＝BC かつ BC＝AQ なので、 RA ＝ AQ である。

次に、点Aから対辺BCまたはその延長上に垂線ADを引く。 すると、 RQ // BC の仮定により、平行な2直線の同位角が等しい事を利用して、

AD ⊥ RQ

が導かれる。したがって、この線分ADは、△RQPの辺RQの垂直二等分線である。

同様に考えると、頂点Bから辺ACまたはその延長上に降ろした垂線BEは辺RPの垂直二等分線であり、頂点Cから辺ABまたはその延長上に降ろした垂線CFは辺PQの垂直二等分線であることがわかる。

この3本の垂直二等分線は、△RQPの外心で交わる。すなわち△ABCの各頂点から対辺に引いた3本の垂線 AD,BE,CF は一点で交わる。

三角形の角の二等分線と辺の比

三角形の角の二等分線に関して、次のことが成り立つ。

三角形の角の2等分線と辺の比

$\triangle ABC$ の $\angle A$ の二等分線と辺BCとの交点をDとすると、$AB:AC=BD:DC$ となる。

• 証明

$\angle A$ の2等分線と辺BCとの交点がDだから

$\angle BAD=\angle DAC$

Cを通りADに平行な直線とBAの延長との交点をEとする。
ADとECは平行であるから

$\angle BAD=\angle AEC$

$\angle DAC=\angle ACE$

上の3つの式から

$\angle AEC=\angle ACE$

よって

$AE=AC$ ……(1)

また、ADとECは平行であるから

$BD:DC=BA:AE$ ……(2)

(1)と(2)より

$AB:AC=BD:DC$

三角形の外角の2等分線に関して、次のことが成り立つ。

三角形の外角の二等分線と辺の比

$\triangle ABC$ の $\angle A$ の外角の二等分線と辺BCの延長との交点をDとすると、$AB:AC=BD:DC$ となる。ただし、$AB\neq AC$ とする。

• 証明

Cを通りADに平行な直線とABの延長との交点をEとすると、上の定理と同様に

$BD:DC=BA:AE=AB:AC$

円の性質

円周角の定理の逆

円周上に3点A,B,Cがある。直線ABについて点Cと同じ側に点Pをとり、$\angle APB$ と $\angle ACB$ の大きさを比べる。

点Pについては、

(1)　Pが円周上にある

(2)　Pが円の内部にある

(3)　Pが円の外部にある

のいずれかである。

(2)の場合、三角形の外角と内角の間の大小関係より

$\angle APB>\angle ACB$

(3)の場合も、三角形の外角と内角の間の大小関係より

$\angle APB<\angle ACB$

この結果、次のことがいえる。

(1)　Pが円周上にある $\Rightarrow \angle APB=\angle ACB$

(2)　Pが円の内部にある $\Rightarrow \angle APB>\angle ACB$

(3)　Pが円の外部にある $\Rightarrow \angle APB<\angle ACB$

このことから、次のようなことがいえる。

円周角の定理の逆

2点C,Pが直線ABについて同じ側にあるとき、$\angle APB=\angle ACB$ ならば、4点A,B,C,Pは同じ円周上にある。

円に内接する四角形

上の議論から三角形に外接する円はどのような三角形を取ったとしても常に存在 することが分かった。しかし、四角形に関してはそれに対して外接するような 円は常に存在するわけではない。 一般に円に内接するような四角形に関しては以下の性質が成り立つ。

円に内接する四角形の性質(1)

円に内接する四角形の相対する角の和は$180^{\circ }$となる。

• 証明

内接する四角形の頂点を反時計回りにA,B,C,Dとする。 このとき、角A,角Cはそれぞれ点B,Dを対応する端点とする円弧に対する円周角となっている。ただし、角Aと角Cは互いに逆の円弧を対応する弧としているため、2つの弧を合わせるとそれらの弧はちょうど円周をおおうことになる。 このため、これらの2つの弧に対応する中心角の和は$360^{\circ }$に対応し、同じ弧に対応する円周角の和は $180^{\circ }$に対応するのである。

また、円に内接する四角形に関して以下の性質も成り立つ。

円に内接する四角形の性質(2)

円に内接する四角形において、1つの内角は、それに向かい合う内角の隣にある外角に等しい。

• 導出

円に内接する四角形ABCDにおいて、上の定理より

$\angle A+\angle C=180^{\circ }$

また、頂点Cにおける外角を $\angle DCE$ とすると、$\angle DCE+\angle C=180^{\circ }$ であるから

$\angle A=\angle DCE$

円に内接する四角形の性質の逆について考えてみよう。

四角形が円に内接する条件

(1)　向かい合う内角の和が$180^{\circ }$の四角形は、円に内接する。 (2)　1つの内角が、それに向かい合う内角の隣にある外角に等しい四角形は、円に内接する。

• 証明

(1)の証明

四角形ABCDで、

$\angle B+\angle D=180^{\circ }$ …(1)

とする。

$\triangle ABC$の外接円Oを書き、円Oに内接する四角形ABCD'を作ると

$\angle B+\angle D'=180^{\circ }$ …(2)

(1),(2)より

$\angle D=\angle D'$

したがって、円周角の定理の逆から、点Dはこの円Oの周上にある。

よって、四角形ABCDは円に内接する。

(2)の証明

四角形ABCDで、頂点Cにおける外角を $\angle DCE$ として、

$\angle A=\angle DCE$

とする。

$\angle DCE+\angle C=180^{\circ }$

であるから

$\angle A+\angle C=180^{\circ }$

四角形が円に内接する条件(1)より、向かい合う内角の和が$180^{\circ }$であるから、四角形ABCDは円に内接する。

接線の長さ

円Oの外の点Aからその円に2本の接線を引ける。その接点をP,Qとするとき、線分AP,AQの長さを、円Oの外の点Aから円Oに引いた接線の長さという。

2つの接線の長さについて、次のことがいえる。

接線の長さ

円外の点からその円に引いた2本の接線の長さは等しい。

• 導出

直角三角形APO,AQOにおいて

$PO=QO$ …(I)

$AO$は共通 …(II)

(I),(II)より

$\triangle APO\equiv \triangle AQO$

よって、対応する辺APとAQは等しい。

接弦定理

円周上の点Aを通る接線ATがあって、円周上に2点B,Cをとるとき、$\angle TAB$ と円周角 $\angle ACB$ の大きさには、次のような関係がある。

接弦定理

円の弦とその一端から引いた接線とのなす角は、その角内にある弧に対する円周角に等しい。

• 証明

$\angle TAB$ が鋭角の場合について考える。

直径ADを引くと、$\angle TAD=90^{\circ }$ であるから、

$\angle TAB=90^{\circ }-\angle BAD$ …(1)

また、ADは直径であるから

$\angle ACD=90^{\circ }$

$\angle ACB=90^{\circ }-\angle BCD$ …(2)

$\angle BAD$ と $\angle BCD$ は弧BDに対する円周角であるから

$\angle BAD=\angle BCD$ …(3)

(1),(2),(3)より

$\angle TAB=\angle ACB$

$\angle TAB$ が直角、鈍角の場合についても同様に証明できる。

方べきの定理

中心Oとする円について次の定理が成り立つ。

方べきの定理

円周上に異なった2点A,Bを取りその2点を通る直線を取る。また、同様に A,Bと異なった2点C,Dを通りそれらを通過する直線を取り、直線ABと直線CDの 交点をEと取る。このとき、 $AE\times BE=CE\times DE$ が成り立つ。この定理を方べきの定理と呼ぶ。

• 証明

まず、点Eが円の外部にある場合を考える。このとき、直線AB上で点Eに近い点を点B, 直線CD上で点Eに近い点を点Cとおいたとき、三角形ECBと三角形EADが相似であることを 示す。

• 図

まず、四角形ABCDは円に内接していることから、

$\angle DAE,\angle BCE$

について、

$\angle DAE=\angle BCE$

が成立する。これは円に内接する四角形の相対する角の和が$180^{\circ }$になることに よっている。同様にして

$\angle ADE=\angle CBE$

が成立し、2角が等しいことから三角形ECBと三角形EADは相似となる。 このことから、

$EC:EA=EB:ED$

となるが、このことは

$EA\times EB=EC\times ED$

に等しい。

次に、点Eが円の内部にある場合を考える。

• 図

このとき三角形EADと三角形EBCが互いに相似であることを示す。 最初に

$\angle AED,\angle CEB$

についてこれらが互いの対頂角であることから

$\angle AED=\angle CEB$

が成り立つ。次に、

$\angle EAD,\angle ECB$

についてこれらが円周BDの円周角であることから

$\angle EAD=\angle ECB$

が成り立つ。よって、2角が等しいことから三角形EADと三角形EBCは 互いに相似である。このことから

$EC:EA=EB:ED$

となるが、このことは

$EA\times EB=EC\times ED$

に等しい。 よって、どちらの場合にも方べきの定理が示された。

また、中心Oとする円の弦と接線について次の定理が成り立つ。

方べきの定理(2)

円の弦ABの延長上の点Pから円に引いた接線をPTとする。このとき、 $PA\times PB=PT^{2}$ が成り立つ。

• 証明

$\triangle PAT$ と $\triangle PTB$ において

接弦定理より

$\angle ATP=\angle TBP$ …(II)

$\angle APT=\angle TPB$（共通） …(II)

だから、$\triangle PAT$ と $\triangle PTB$ は相似

よって、

$PA:PT=PT:PB$

したがって、

$PA\times PB=PT^{2}$

2つの円の位置関係

2つの円を取ったときこれらはいくつかの仕方で関係する。2つの円の関係は2つの円の中心間の距離と、2円の半径によって定まる。 2円の距離をそれぞれ$r_{1}$,$r_{2}$($r_{1}>r_{2}$),中心間の距離を$l$とすると、2円の位置関係として

$l<r_{1}-r_{2}$のとき、円2は円1に含まれている。

$r_{1}-r_{2}=l$のとき、2つの円は内接している。

$r_{1}-r_{2}<l<r_{1}+r_{2}$のとき、円2と円1は互いに交わっている。

$r_{1}+r_{2}=l$のとき、2つの円は外接している。

$r_{1}+r_{2}<l$のとき、2円は離れている。

がある。

2つの円がただ1つの共有点をもつとき、この2つの円は接するといい、この共有点を接点（せってん、英：point of contact）という。

1つの直線が、2つの円に接しているとき、この直線を、2つの円の共通接線という。

$l<r_{1}-r_{2}$のとき、共通接線はない。

$r_{1}-r_{2}=l$のとき、共通接線は1本。

$r_{1}-r_{2}<l<r_{1}+r_{2}$のとき、共通接線は2本。

$r_{1}+r_{2}=l$のとき、共通接線は3本。

$r_{1}+r_{2}<l$のとき、共通接線は4本。