位相幾何学/1次元のトポロジー/1次元複体
1次元の図形を扱った位相幾何学にける基本的な事柄について説明します。
位相幾何学の図形
[編集]幾何学とは、図形をテーマに生み出された学問です。位相幾何学においても、図形を扱っていることに変わりはありません。ユークリッド幾何学で扱うような三角形や四角形も、位相幾何学で扱うことができます。しかし、位相幾何学で図形を扱うときには、ユークリッド幾何学とは違った視点から見なければなりません。
言葉の定義
[編集]まずは、図形を扱うために必要な言葉の確認をしましょう。ここでは、平面での位相幾何学を扱うのに必要な言葉だけを選びました。
- 点
- 空間のある点。広さや大きさの無い図形。
- 線
- 二つの点を結ぶ図形。
- グラフ
- 有限個の点と有限個の線のあつまった図形。
位相幾何学では、点が非常に重要な役割をします。位相幾何学における点には、ユークリッド幾何学にあるような座標を持ちません。単に点があるだけです。そのため、いくつかの点があつまったグラフが描かれても、それにはあまり意味がありません。位相幾何学の視点でそのグラフを見たなら、それは点がただ4つあるだけのことです。
ユークリッド幾何学で考えるような直線の概念も、位相幾何学にはある意味で存在しません。点と点のつながり具合が同じか違うかという点だけに着目しますので、直線か曲線かなどという区別に意味はないのです。
それから、グラフ同士の関係を示す言葉も、ひとつ定義しておきましょう。ユークリッド幾何学などでは、合同に当たる概念です。位相幾何学では、合同な図形はありません。長さや大きさを考えないからです。その代わりに、図形の構造が同じかどうかを考えます。つまり、点がグラフの中でどのように結びついているか、ということが重要なのです。
- 同型
- 位相幾何学の観点で同じ図形であることを、同型であると言います。
これらの言葉だけでは、位相幾何学の図形を扱うには不十分です。けれど、まずは導入として、これらの言葉を用いていくつかの図形を見ていきましょう。
同型なグラフの例
[編集]
たとえば、このような図形が同型です。二つの図形が同型であることは、記号「」を用いて表します。
左側の図形は三角形ですが、四つの点があります。真ん中に、一本の線が入っています。上の下の点を移動させて、線を曲線に書き換えれば、右の図形になります。言葉では分かりにくいかもしれませんね。実際に紙に書いてみるのも手です。自分の頭の中で図形をイメージして、ぐにゃぐにゃと変形するのもいいでしょう。ここで大切なのは、この二つの図形が同型であることに納得することです。
アルファベットを位相幾何学で捉える
[編集]腕ならしに、アルファベットの形を位相同型かどうかで分類してみましょう。
問題
大文字のアルファベット26文字を、同型の図形を集めたグループに分けなさい。
解答例
- Iグループ = C I L M N S U V W Z
- Tグループ = E F J T Y
- Hグループ = G H K
- Rグループ = A R
- Oグループ = D O
- Bグループ Bのみ
- Pグループ Pのみ
- Qグループ Qのみ
- Xグループ Xのみ
ただし、アルファベットの形はフォントによって異なるため、この分類とは別の分類が正しくなることもあるでしょう。
ケーニヒスベルクの橋
[編集]
位相幾何学の出発点とも言える有名な問題です。「ケーニヒスベルクの橋渡り」とか「ケーニヒスベルクの橋の問題」とか言いますが、どんな表現でも変わりません。
問題
ケーニヒスベルクという昔の大きな町には、プルーゲルという大きな川が流れていた。右の図のように、3つの岸と1つの島が橋で結ばれている。このとき、ある場所から出発して、同じ橋を2度渡らずに全ての橋を渡り、最初の場所に戻ってくるような道はあるか。
解答
そのような道は無い。
ヒント
この問題は、次の図形が一筆書きできるか、という問いかけです。

青い点が岸と島を、線が橋を表しています。グラフに直すと簡単ですね。さて、このグラフは一筆書きができるのでしょうか? 一筆書きができるグラフとは、どのようなグラフなのでしょうか? その条件が整理できれば、この問題は簡単です。
1次元複体
[編集]1次元複体とは、これまでに述べたようなことを少し厳密に扱うための概念です。基本的な定義についてしっかりと理解しましょう。ではまず、1次元複体を定義するために必要な単体についてお話します。
単体
[編集]単体とは、図形をつくる一番小さな単位のことです。
- 0次元単体
- 点のこと。
- 1次元単体
- 二つの異なる0次元単体とそれらを結ぶ線とが合わさったもの。
- 開いた1次元単体
- 1次元単体から両端の0次元単体を取り除いたもの。
- 面
- 0次元単体xにおいて、x自身をxの面という。
- 1次元単体|xy|において、0次元単体x、0次元単体yおよび1次元単体|xy|を、|xy|の面という。
2次元単体や3次元単体も存在しますが、ここでは1次元単体までを扱います。章の名前が一次元のトポロジーとされているのは、そのためです。なにも、1次元空間上の位相幾何学という意味ではありません。
1次元複体
[編集]それでは、0次元単体や1次元単体の複合体として、1次元複体を考えて行きましょう。まずは、1次元複体の定義からです。
- 1次元複体
- 0次元単体と1次元単体の集合として描かれる図形であって、その1次元単体の両端の0次元単体は、必ずその1次元複体に属するもの。
1次元複体の例
[編集]いくつかの1次元複体を見て、1次元複体のイメージをつかんでください。
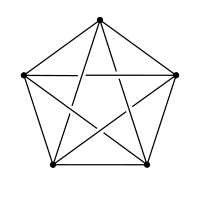
これは、五点完全グラフと呼ばれます。1次元複体であることは直観的に理解できることだと思います。

