利用者:YMobi/Haskell/Zipper

テセウスとZipper

迷宮

「テセウス、何か手を打たなければならない。」ホメロス…Ancient Geeks株式会社の営業部部長は言った。テセウスはミノタウロスアクションフィギュア™を後ろの棚に入れてうなずいた。「今の子供たちはもはや古代神話に興味を持っていない、彼らはスパイダーマンやスポーンのような現代ヒーローが好きなんだ。」ヒーロー。テセウスは、迷宮からクレタ島に戻った英雄だったから、どのくらいのものかをよく知っていた。しかし「現代ヒーロー」たちは現実的に現れるようなことはしなかった。何が彼らの勝因だったのか？とにかく、未払い金の問題が解決できなかった場合、株主たちはステュクス河を渡ってきてAncient Geeks株式会社を整理するだろう。

"Theseus, we have to do something" said Homer, chief marketing officer of Ancient Geeks Inc.. Theseus put the Minotaur action figure™ back onto the shelf and nodded. "Today's children are no longer interested in the ancient myths, they prefer modern heroes like Spiderman or Sponge Bob." Heroes. Theseus knew well how much he had been a hero in the labyrinth back then on Crete. But those "modern heroes" did not even try to appear realistic. What made them so successful? Anyway, if the pending sales problems could not be resolved, the shareholders would certainly arrange a passage over the Styx for Ancient Geeks Inc.

「閃いたぞ！テセウス、良い案がある！君のミノタウロスとの戦いの物語をコンピューターゲームにするんだ！どうだい？」ホメロスは正しかった。何冊かの本、叙事詩の歌(ヒットチャートは総なめ)、必須の映画三部作、そして数え切れないテセウスとミノタウロス™のギミックは出してきた。しかしコンピューターゲームは盲点だった。「完璧だよ。テセウス、すぐにゲームの開発に取りかかるんだ。」

"Heureka! Theseus, I have an idea: we implement your story with the Minotaur as a computer game! What do you say?" Homer was right. There had been several books, epic (and chart breaking) songs, a mandatory movie trilogy and uncountable Theseus & the Minotaur™ gimmicks, but a computer game was missing. "Perfect, then. Now, Theseus, your task is to implement the game".

真の英雄、テセウスは会社の命運を賭けた製品の開発言語にHaskellを選択した。もちろん、迷宮のミノタウロスを見つけ出すのがこのゲームの売りの一つになった。彼は熟考した。「二次元の迷宮はいろいろな方向に進むことができる。角度や距離といった詳細も抽象化できないとな。脱出方法を見つけるために、経路がどのように分かれるかを知っておく必要があるな。シンプルさを維持するには、迷宮は木構造をモデルにしよう。これなら、どこまで深く歩いても二股が再び合流することはないからプレイヤーが同じ所をぐるぐる廻ることはない。しかし、迷子になる機会は十分あるとおもう。それにヘビープレイヤーなら、左手の法則で迷路全体を探索することができる。」

A true hero, Theseus chose Haskell as the language to implement the company's redeeming product in. Of course, exploring the labyrinth of the Minotaur was to become one of the game's highlights. He pondered: "We have a two-dimensional labyrinth whose corridors can point in many directions. Of course, we can abstract from the detailed lengths and angles: for the purpose of finding the way out, we only need to know how the path forks. To keep things easy, we model the labyrinth as a tree. This way, the two branches of a fork cannot join again when walking deeper and the player cannot go round in circles. But I think there is enough opportunity to get lost; and this way, if the player is patient enough, he can explore the entire labyrinth with the left-hand rule."

data Node a = DeadEnd a
            | Passage a (Node a)
            | Fork    a (Node a) (Node a)

迷宮とその木構造による表現の例An example labyrinth and its representation as tree.

テセウスは迷路のノードにパラメータを運ぶa型を追加して作り上げた。後で、ここにはノードが指定する座標、その周辺の雰囲気、床の上に落ちているアイテムのリスト、迷宮を彷徨うモンスターのような、ゲーム関連の情報を保持することができる。Node aの全てのコンストラクタの最初の引数に格納されている、a型の値を変更したり取得したりする二つのヘルパー関数を仮定しよう。

Theseus made the nodes of the labyrinth carry an extra parameter of type a. Later on, it may hold game relevant information like the coordinates of the spot a node designates, the ambience around it, a list of game items that lie on the floor, or a list of monsters wandering in that section of the labyrinth. We assume that two helper functions

get :: Node a -> a
put :: a -> Node a -> Node a

retrieve and change the value of type a stored in the first argument of every constructor of Node a.

演習
getとputを実装せよ。getの実装の一つは以下のようになる。 get (Passage x _) = x。 具体的な例を得るために、Node (Int,Int)の値を図にして迷路を表示するコードを書け。追加のパラメータ(Int,Int)はノードのデカルト座標系を保持するものとする。

「むむー、迷宮内のプレイヤーの現在位置はどのように表現しよう？プレイヤーは分岐を左か右のどちらへ進むか選択して深くへ潜っていけるとすると、こんな感じか」

"Mh, how to represent the player's current position in the labyrinth? The player can explore deeper by choosing left or right branches, like in"

 turnRight :: Node a -> Maybe (Node a)
 turnRight (Fork _ l r) = Just r
 turnRight _            = Nothing

「しかし、現在の迷宮のトップをサブ迷宮で置き換える方法は使えないな。戻れなくなってしまう。」彼は熟考した。「ああ、戻るためにはアリアドネの糸のトリックが使えるな。プレイヤーの位置を「辿ってきた分岐のリスト」にすれば単純に表現できる。「分岐のリスト」の糸を辿って戻ることもできるし、迷路は常に同じままだ。」

"But replacing the current top of the labyrinth with the corresponding sub-labyrinth this way is not an option, because he cannot go back then." He pondered. "Ah, we can apply Ariadne's trick with the thread for going back. We simply represent the player's position by the list of branches his thread takes, the labyrinth always remains the same."

data Branch = KeepStraightOn
            | TurnLeft
            | TurnRight
type Thread = [Branch]

アリアドネの糸によるプレイヤーの位置の表現。Representation of the player's position by Ariadne's thread.

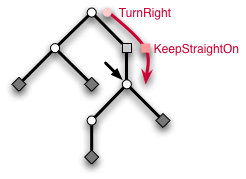
「例えば、[TurnRight,KeepStraightOn]という糸は、プレイヤーがエントランスから右へ分岐して、その後Passageをまっすぐ進んで現在の位置に辿り着いたということを意味する。糸をプレイヤーが伸ばしたり短くしたりすることによって迷路を探索することができる。具体的には、turnRight関数はTurnRightを追加することによって糸を伸ばす。」

"For example, a thread [TurnRight,KeepStraightOn] means that the player took the right branch at the entrance and then went straight down a Passage to reach its current position. With the thread, the player can now explore the labyrinth by extending or shortening it. For instance, the function turnRight extends the thread by appending the TurnRight to it."

turnRight :: Thread -> Thread
turnRight t = t ++ [TurnRight]

「アイテムのようなゲームに関連する追加のデータにアクセスするには、単純に糸から迷路に従えばいい。」 "To access the extra data, i.e. the game relevant items and such, we simply follow the thread into the labyrinth."

retrieve :: Thread -> Node a -> a
retrieve []                  n             = get n
retrieve (KeepStraightOn:bs) (Passage _ n) = retrieve bs n
retrieve (TurnLeft      :bs) (Fork _ l r)  = retrieve bs l
retrieve (TurnRight     :bs) (Fork _ l r)  = retrieve bs r

演習
プレイヤー位置上の追加データにa -> a型の関数を適用するupdate関数を書け。

この解決策はテセウスが満足するに至らなかった。「なんてこった、経路を伸ばしたり戻ったりする場合、リストの最後の要素を変更しなければならないじゃないか。リストを逆順に格納することはできるが、今度は迷宮内のプレイヤーの位置にアクセスするために何度も何度も糸を辿らないといけない。どちらのアクションも、糸の長さに比例した時間がかかってしまう。大規模な迷路ならこれはあまりにも長すぎる。他に方法はないのか？」

Theseus' satisfaction over this solution did not last long. "Unfortunately, if we want to extend the path or go back a step, we have to change the last element of the list. We could store the list in reverse, but even then, we have to follow the thread again and again to access the data in the labyrinth at the player's position. Both actions take time proportional to the length of the thread and for large labyrinths, this will be too long. Isn't there another way?"

アリアドネのZipper

テセウスは熟練した戦士だったが、プログラミング技術を修練したわけではなかったので、満足のいく解決策を見つけることはできなかった。強烈ながらも無益な思考の後に、以前愛したアリアドネに電話して助言を求めることにした。結局のところ、糸のアイディアを持っていたのは彼女だったからだ。
"アリアドネコンサルティングです。ご用件を伺います"
我らが英雄はその声をすぐさま理解した。
「やあ、アリアドネ、テセウスだ。」
気まずい沈黙が会話を停止させた。彼女をナクソス島に捨てたテセウスが何故電話してきたのか理解していない事を思い出した。しかし、ハデスの道を逝くAncent Geeks株式会社、彼に選択の余地はなかった。
「ぁあ…、最愛の人、…元気だったかい？」
アリアドネは冷たい反応を返した。"テセウスさん、今更”最愛の人”？何がしたいの？"
「えぇっと…、実は…実はな。プログラミングの問題で助けが必要なんだ。新しいコンピューターゲーム『テセウスとミノタウロス™』をプログラミング中なんだ。」
彼女はあざけ笑った。"また別の芸術であなたの”英雄的存在”を美化するの？全て人々を助けるあなたが、私の助けを欲しいと？"
「アリアドネ、どうか頼む。Ancient Geeks株式会社は破産の危機にひんしている。このゲームが最後の望みなんだ！」
少し待った後、彼女は決定を下した。
"いいでしょう、手を貸します。ただしAncient Geeks株式会社からかなりの部分を売却して頂きます。30%ってとこかしら。"
テセウスは青ざめた。しかし他に何が出来るだろうか？状況は十分ひっ迫していたので、彼はアリアドネの取り分を10%で交渉し合意した。 While Theseus was a skillful warrior, he did not train much in the art of programming and could not find a satisfying solution. After intense but fruitless cogitation, he decided to call his former love Ariadne to ask her for advice. After all, it was she who had the idea with the thread.
"Ariadne Consulting. What can I do for you?"
Our hero immediately recognized the voice.
"Hello Ariadne, it's Theseus."
An uneasy silence paused the conversation. Theseus remembered well that he had abandoned her on the island of Naxos and knew that she would not appreciate his call. But Ancient Geeks Inc. was on the road to Hades and he had no choice.
"Uhm, darling, ... how are you?"
Ariadne retorted an icy response, "Mr. Theseus, the times of darling are long over. What do you want?"
"Well, I uhm ... I need some help with a programming problem. I'm programming a new Theseus & the Minotaur™ computer game."
She jeered, "Yet another artifact to glorify your 'heroic being'? And you want me of all people to help you?"
"Ariadne, please, I beg of you, Ancient Geeks Inc. is on the brink of insolvency. The game is our last hope!"
After a pause, she came to a decision.
"Fine, I will help you. But only if you transfer a substantial part of Ancient Geeks Inc. to me. Let's say thirty percent."
Theseus turned pale. But what could he do? The situation was desperate enough, so he agreed but only after negotiating Ariadne's share to a tenth.

テセウスが、彼が念頭に置いていた迷宮の表現をアリアドネに語ると、彼女はすぐさまアドバイスをくれた。
"あなたが必要なのはzipperね。"
「えっ？私の"社会の窓"に何か問題あるかい？」
"何も。このデータ構造はGérard Huetによって最初に発表されたわ。"
「へえ」
"より正確には、リストや二分木のようなツリー型データ構造に対して、純粋に関数的な方法で焦点を当てたり、データ構造内のサブツリーの一点を指して、定数時間で更新や参照を可能にする方法ね。。私たちの場合では、プレイヤーの位置に焦点を当てましょう。"
「高速な更新が必要なことはわかっているけど、どのようにコーディングしたらいいんだい？」
"せっかちね、コーディングによって問題を解決することはできないわ。あなたの思考だけが問題を解決できるの。 純粋関数型のデータ構造で定数時間で更新できるのは最上位ノードだけね。だから焦点は必ず最上部にする必要があるわ。現在、あなたの迷宮の最上位ノードは常に入り口だけど、あなたが以前思いついたサブ迷宮で置き換えるアイディアはプレイヤーの位置が最上位ノードであることを保証します。"
「けど、問題はどうやって戻ればいいんだい？サブ迷宮はプレイヤーがどう分岐してきたかが全て失われてしまう。」
"えーと、サブ迷宮サブ迷宮を失わないために糸が使えるわ。" アリアドネはテセウスが困惑するのを満喫できましたが、彼が既にアリアドネの糸を使用したことに不満を言う隙を与えず、
"鍵は糸にサブ迷宮をくっつけること、実際にはまったく失われないようにね。この意図は、糸と現在のサブ迷宮をお互いに補完させて迷宮全体とするの。サブ迷宮は'現在'プレイヤーが経っている場所を意味します。zipperは単純に糸と現在のサブ迷宮で構成されています。"

After Theseus told Ariadne of the labyrinth representation he had in mind, she could immediately give advice,
"You need a zipper."
"Huh? What does the problem have to do with my fly?"
"Nothing, it's a data structure first published by Gérard Huet."
"Ah."
"More precisely, it's a purely functional way to augment tree-like data structures like lists or binary trees with a single focus or finger that points to a subtree inside the data structure and allows constant time updates and lookups at the spot it points to. In our case, we want a focus on the player's position."
"I know for myself that I want fast updates, but how do I code it?"
"Don't get impatient, you cannot solve problems by coding, you can only solve them by thinking. The only place where we can get constant time updates in a purely functional data structure is the topmost node. So, the focus necessarily has to be at the top. Currently, the topmost node in your labyrinth is always the entrance, but your previous idea of replacing the labyrinth by one of its sub-labyrinths ensures that the player's position is at the topmost node."
"But then, the problem is how to go back, because all those sub-labyrinths get lost that the player did not choose to branch into."
"Well, you can use my thread in order not to lose the sub-labyrinths."
Ariadne savored Theseus' puzzlement but quickly continued before he could complain that he already used Ariadne's thread,
"The key is to glue the lost sub-labyrinths to the thread so that they actually don't get lost at all. The intention is that the thread and the current sub-labyrinth complement one another to the whole labyrinth. With 'current' sub-labyrinth, I mean the one that the player stands on top of. The zipper simply consists of the thread and the current sub-labyrinth."

type Zipper a = (Thread a, Node a)

zipperはアリアドネの糸と現在プレイヤーが立っているサブ迷宮の組。メインの糸は赤色でサブ迷宮はそこに接続されており、そのような迷宮全体は組から再構築できる。The zipper is a pair of Ariadne's thread and the current sub-labyrinth that the player stands on top. The main thread is colored red and has sub-labyrinths attached to it, such that the whole labyrinth can be reconstructed from the pair.

テセウスは何も言わなかった。
"また、現在のサブ迷宮が置かれている糸のコンテキストを表示することができるわ。ところで、Threadはサブ迷宮を格納するためにaという追加パラメータを取る必要があるわね。糸はまだ単純な分岐のリストだけど、分岐は以前とは異なっているわ。"

Theseus didn't say anything.
"You can also view the thread as a context in which the current sub-labyrinth resides. Now, let's find out how to define Thread a. By the way, Thread has to take the extra parameter a because it now stores sub-labyrinths. The thread is still a simple list of branches, but the branches are different from before."

data Branch a  = KeepStraightOn a
               | TurnLeft  a (Node a)
               | TurnRight a (Node a)
type Thread a  = [Branch a]

"もっとも重要なのは、TurnLeftとTurnRightはサブ迷宮をくっつけるということ。プレイヤーが右へ曲がる時、TurnRightと今は辿れない左の分岐を取り付けて糸を拡張し、それが失われないようにしなければ。"
テセウスが遮った、「待ってくれ、turnRightのような関数をどのように実装したらいいんだ？TurnRightの最初の引数の型aは何にすればいいんだ？あぁ、わかった。失われてしまう分岐はくっつける必要はないが、Forkの追加データも同様に失われてしまう。けど、予備を使って新しい分岐を生成できる。

"Most importantly, TurnLeft and TurnRight have a sub-labyrinth glued to them. When the player chooses say to turn right, we extend the thread with a TurnRight and now attach the untaken left branch to it, so that it doesn't get lost."
Theseus interrupts, "Wait, how would I implement this behavior as a function turnRight? And what about the first argument of type a for TurnRight? Ah, I see. We not only need to glue the branch that would get lost, but also the extra data of the Fork because it would otherwise get lost as well. So, we can generate a new branch by a preliminary"

branchRight (Fork x l r) = TurnRight x l

「何らかの方法で既存の糸を拡張する必要があるな。」
"確かに。第二のポイントは糸に新しい分岐を追加するときは後ろから入れていくことよ。伸ばすときは新しい分岐をリストの前面に置く。戻るには最初の要素を削除すればいいわね。"
なるほど、これは伸ばすときと戻るときだけ定数時間になって、以前のバージョンのような長さに比例した時間がかかることはないわけだ。だからturnRightの最終バージョンは…」

"Now, we have to somehow extend the existing thread with it."
"Indeed. The second point about the thread is that it is stored backwards. To extend it, you put a new branch in front of the list. To go back, you delete the topmost element."
"Aha, this makes extending and going back take only constant time, not time proportional to the length as in my previous version. So the final version of turnRight is"

turnRight :: Zipper a -> Maybe (Zipper a)
turnRight (t, Fork x l r) = Just (TurnRight x l : t, r)
turnRight _               = Nothing

入り口から右のサブツリーを取る。もちろん、糸は最初は空である。糸は後ろ向きに実行することに注意する、すなわち最上位のセグメントは最も最近のもの。Taking the right subtree from the entrance. Of course, the thread is initially empty. Note that the thread runs backwards, i.e. the topmost segment is the most recent.

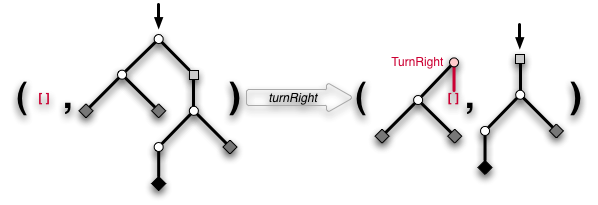
「これは簡単だった。よし、続けて回廊を真っ直ぐ進むkeepStraightOnに取りかかろう。これは追加のデータを維持するのが必要な分岐の選択よりも簡単だ。」

"That was not too difficult. So let's continue with keepStraightOn for going down a passage. This is even easier than choosing a branch as we only need to keep the extra data:"

keepStraightOn :: Zipper a -> Maybe (Zipper a)
keepStraightOn (t, Passage x n) = Just (KeepStraightOn x : t, n)
keepStraightOn _                = Nothing

回廊を真っ直ぐ進む。

演習
turnLeft関数を書け。

嬉しそうに彼は続け、「しかし興味深いのは戻っていくときだな。やってみよう…」

Pleased, he continued, "But the interesting part is to go back, of course. Let's see..."

back :: Zipper a -> Maybe (Zipper a)
back ([]                   , _) = Nothing
back (KeepStraightOn x : t , n) = Just (t, Passage x n)
back (TurnLeft  x r    : t , l) = Just (t, Fork x l r)
back (TurnRight x l    : t , r) = Just (t, Fork x l r)

「もし糸が空なら、まだ迷宮の入り口で戻ることはできない。それ以外の場合は、糸を巻かなければならない。糸につなげたおかげで、実際に来た道からサブ迷宮を再構築することができる。」
アリアドネが言った。"部分テストは、左側のx、l、rのような各束縛変数が右辺に一度だけ現れているか確認するためであることに注意して。だから、zipperを上下に歩くとき、糸と現在のサブ迷宮を再配布するだけでいいわ。"

"If the thread is empty, we're already at the entrance of the labyrinth and cannot go back. In all other cases, we have to wind up the thread. And thanks to the attachments to the thread, we can actually reconstruct the sub-labyrinth we came from."
Ariadne remarked, "Note that a partial test for correctness is to check that each bound variable like x, l and r on the left hand side appears exactly once at the right hands side as well. So, when walking up and down a zipper, we only redistribute data between the thread and the current sub-labyrinth."

演習
今やzipperの中を移動することができるようになった。プレイヤーの位置の追加データを操作する関数get、put、updateを書け。 zipperはNode aのような具体例に制限されることはないので、全ての木構造のようなデータ型で構成することができる。最初に戻って、以下の二分木のzipperを構築し、糸が取ることの出来る可能な分岐について考えよ。木を探索するときに糸へ何をくっつけるべきだろうか？ data Tree a = Leaf a | Bin (Tree a) (Tree a) 単純なリストも同様にzipperにできる。 data List a = Empty | Cons a (List a) これは何に見えるだろうか？ テセウスの迷宮ゲームを完成させよ。

演習

Now that we can navigate the zipper, code the functions get, put and update that operate on the extra data at the player's position. Zippers are by no means limited to the concrete example Node a, they can be constructed for all tree-like data types. Go on and construct a zipper for binary trees data Tree a = Leaf a | Bin (Tree a) (Tree a) Start by thinking about the possible branches Branch a that a thread can take. What do you have to glue to the thread when exploring the tree? Simple lists have a zipper as well. data List a = Empty | Cons a (List a) What does it look like? Write a complete game based on Theseus' labyrinth.

わかったぞ！これは一部をアリアドネコンサルティングに売却したとしても、Ancient Geeks株式会社が優先すべき、テセウスが求めていた解決策だった。しかし一つだけ疑問が残った。
「なんでzipperと呼ばれているんだ？」
"そうね、'アリアドネの真珠のネックレス'と呼ぶべきでしょうね。でもたいていの場合で、zipperと呼ばれるのは衣服のチャックの開いている部分を糸、閉じている部分をサブ迷宮とするアナロジーね。データ構造内の移動がチャックを上げ下げするのに似ているから。"
「アリアドネの真珠のネックレス、ね…。」彼は軽蔑を向けた。「君の糸に助けられたよ。クレタ島の時のように」
"あのときの糸のアイディアはあなた次第で、"彼女は答えた。
「フン、もう糸は必要ない。」
彼の驚いたことに、彼女は同意して、"そうね、確かにもう糸は必要ないわね。別の視点では文字通り指差した木の焦点を掴んで下から持ち上げることね。焦点が上になって他の全ての枝は垂れ下がる。結果、木に適合する代数的データ型はzipperになる可能性が最も高いわね。"

Heureka! That was the solution Theseus sought and Ancient Geeks Inc. should prevail, even if partially sold to Ariadne Consulting. But one question remained:
"Why is it called zipper?"
"Well, I would have called it 'Ariadne's pearl necklace'. But most likely, it's called zipper because the thread is in analogy to the open part and the sub-labyrinth is like the closed part of a zipper. Moving around in the data structure is analogous to zipping or unzipping the zipper."
"'Ariadne's pearl necklace'," he articulated disdainfully. "As if your thread was any help back then on Crete."
"As if the idea with the thread were yours," she replied.
"Bah, I need no thread," he defied the fact that he actually did need the thread to program the game.
Much to his surprise, she agreed, "Well, indeed you don't need a thread. Another view is to literally grab the tree at the focus with your finger and lift it up in the air. The focus will be at the top and all other branches of the tree hang down. You only have to assign the resulting tree a suitable algebraic data type, most likely that of the zipper."

指で焦点を掴み、下から持ち上げると枝がぶら下がって指差したノードをトップとする新しい木が形成され、代数的データ型で構成する準備が整う。Grab the focus with your finger, lift it in the air and the hanging branches will form new tree with your finger at the top, ready to be structured by an algebraic data type.

「ああ。」彼はアリアドネの糸はもう必要としていないが、アリアドネは必要だという事を伝えようとしている？その言葉はあまりに饒舌だった。
「ありがとう、アリアドネ。元気で」
電話を介していて直接見ることはできなかったが、彼女は作り笑いを隠さなかった。

"Ah." He didn't need Ariadne's thread but he needed Ariadne to tell him? That was too much.
"Thank you, Ariadne, good bye."
She did not hide her smirk as he could not see it anyway through the phone.

演習
リストを一つとり、指で真ん中の要素を修正し、リストを下から持ち上げる。結果の木はどのような種類になるだろうか？

演習
Take a list, fix one element in the middle with your finger and lift the list into the air. What type can you give to the resulting tree?

半年が過ぎ、テセウスはショッピングウィンドウの前で立ち止まった。冷たい雨に逆らうため防寒着のフードを被った。点滅する文字が告げていたのは…。

"Spider-Man: lost in the Web"

- 糸の迷宮から君の方法を見つけ出せ -
Ancient Geeks株式会社が送る最高のコンピューターゲーム

彼はアリアドネに電話した日を呪って、会社の一部を彼女に売却した。 WineOS社による不自然な敵対的買収は彼女の仕業だったのだろうか。アリアドネの夫ディオニソスが率いていたのだろうか？テセウスはガラス窓の下に落ちる雨を見つめた。生産ラインが変更されれば、もう誰もミノタウロス™とテセウスの商品を生産しないだろう。彼はため息をついた。彼の時間、英雄の時間は終わりを告げた。今はスーパーヒーローの時代が来たのだ。

Half a year later, Theseus stopped in front of a shop window, defying the cold rain that tried to creep under his buttoned up anorak. Blinking letters announced

"Spider-Man: lost in the Web"

- find your way through the labyrinth of threads -
the great computer game by Ancient Geeks Inc.

He cursed the day when he called Ariadne and sold her a part of the company. Was it she who contrived the unfriendly takeover by WineOS Corp., led by Ariadne's husband Dionysus? Theseus watched the raindrops finding their way down the glass window. After the production line was changed, nobody would produce Theseus and the Minotaur™ merchandise anymore. He sighed. His time, the time of heroes, was over. Now came the super-heroes.

データ型の微分

前のセクションでzipperを提示したが、別のサブツリーに焦点を当てる事ができる指で、ツリーのようなデータ構造Node aを強化する方法がある。特定のデータ構造Node aのzipperを構築子ながら、異なる木構造をつなげて構築することは手で簡単に行うことができる。

演習
三分木から始めよう。 data Tree a = Leaf a | Node (Tree a) (Tree a) (Tree a) と対応するThread aとZipper aを導出せよ。

The previous section has presented the zipper, a way to augment a tree-like data structure Node a with a finger that can focus on the different subtrees. While we constructed a zipper for a particular data structure Node a, the construction can be easily adapted to different tree data structures by hand.

演習
Start with a ternary tree data Tree a = Leaf a | Node (Tree a) (Tree a) (Tree a) and derive the corresponding Thread a and Zipper a.

機械的な微分

しかし任意の(適切な正規の)データ型のzipperは機械的に導出することもできる。驚くべき事に、「導出（derive）」は文字通りの意味で、zipperはデータ型の導関数(derivative)によって得ることが出来る。最初の発見はConor McBrideによって述べられた。以降のセクションでは、この本当にすばらしい数学の宝石を解明しよう。

But there is also an entirely mechanical way to derive the zipper of any (suitably regular) data type. Surprisingly, 'derive' is to be taken literally, for the zipper can be obtained by the derivative of the data type, a discovery first described by Conor McBride. The subsequent section is going to explicate this truly wonderful mathematical gem.

体系的な構成のため、私たちは型の計算が必要になる。型の構造的な計算の基礎はGeneric Programmingの章で概説されており、この素材に大きく頼っている。

For a systematic construction, we need to calculate with types. The basics of structural calculations with types are outlined in a separate chapter Generic Programming and we will heavily rely on this material.

zipperが共通に持っているものと、どのように微分を仄めかしているのかを理解するためにいくつかの例を見ていこう。二分木の型は漸化式の不動点で、

Let's look at some examples to see what their zippers have in common and how they hint differentiation. The type of binary tree is the fixed point of the recursive equation

${\mathit {Tree2}}=1+{\mathit {Tree2}}\times {\mathit {Tree2}}$.

木を渡り歩くとき、左または右のサブツリーに入ることを繰り返し選択し、アリアドネの糸には入らなかった方のサブツリーをくっつける。したがって、糸の枝は次の型を持つ。 When walking down the tree, we iteratively choose to enter the left or the right subtree and then glue the not-entered subtree to Ariadne's thread. Thus, the branches of our thread have the type

${\mathit {Branch2}}={\mathit {Tree2}}+{\mathit {Tree2}}\cong 2\times {\mathit {Tree2}}$.

同様に、三分木 Similarly, the thread for a ternary tree

${\mathit {Tree3}}=1+{\mathit {Tree3}}\times {\mathit {Tree3}}\times {\mathit {Tree3}}$

は次のような型の枝を持つ。 has branches of type

${\mathit {Branch3}}=3\times {\mathit {Tree3}}\times {\mathit {Tree3}}$

なぜなら全ての段階で、3つのサブツリーを選択でき、入らなかった二つのサブツリーを格納しなければならない。これは微分 ${\frac {d}{dx}}x^{2}=2\times x$や${\frac {d}{dx}}x^{3}=3\times x^{2}$とは似ても似つかないと思うだろうか？ because at every step, we can choose between three subtrees and have to store the two subtrees we don't enter. Isn't this strikingly similar to the derivatives ${\frac {d}{dx}}x^{2}=2\times x$ and ${\frac {d}{dx}}x^{3}=3\times x^{2}$?

謎を解く鍵は、データ構造のワンホールコンテキスト(one-hole context)の概念だ。$X$型をパラメタライズしたデータ構造、${\mathit {Tree}}\,X$型のようなものを想像しよう。この$X$型の要素を構造から一つ削除して、なんらかの方法でその位置を空とマークした場合、「マークした穴(hole)」とデータ構造を得られる。結果は「ワンホールコンテキスト」と呼ばれ、「穴」に$X$型の要素を挿入すると完全に満たされた${\mathit {Tree}}\,X$が戻ってくる。「穴」は、位置の識別、焦点の役割を果たす。図でこれを説明しよう。 The key to the mystery is the notion of the one-hole context of a data structure. Imagine a data structure parameterised over a type $X$, like the type of trees ${\mathit {Tree}}\,X$. If we were to remove one of the items of this type $X$ from the structure and somehow mark the now empty position, we obtain a structure with a marked hole. The result is called "one-hole context" and inserting an item of type $X$ into the hole gives back a completely filled ${\mathit {Tree}}\,X$. The hole acts as a distinguished position, a focus. The figures illustrate this.

${\mathit {Tree}}\,X$から$X$型の値を削除するとその位置に穴を残す。Removing a value of type $X$ from a ${\mathit {Tree}}\,X$ leaves a hole at that position.

ワンホールコンテキストに$X$を差し込むより抽象的な説明。A more abstract illustration of plugging $X$ into a one-hole context.

もちろん、我々の興味はワンホールコンテキストに与える型、すなわちHaskellでこれをどのように表現するかだ。問題は焦点を効率よくマークするにはどうしたらいいだろうか。しかし我々が見るように、型の構造に関する帰納法によってワンホールコンテキストの表現を見つけだし、効率的なデータ型につながるワンホールコンテキストを自動的に取得したいと思う。さて、データ構造$F\,X$と関手$F$、そして引数の型$X$を与えよう。$\partial F$という表記法を選択する理由は既におわかりと思うが、ワンホールコンテキストの加法、乗法、合成の法則は、まさに微分におけるライプニッツ則である。

Of course, we are interested in the type to give to a one-hole context, i.e. how to represent it in Haskell. The problem is how to efficiently mark the focus. But as we will see, finding a representation for one-hole contexts by induction on the structure of the type we want to take the one-hole context of automatically leads to an efficient data type. So, given a data structure $F\,X$ with a functor $F$ and an argument type $X$, we want to calculate the type $\partial F\,X$ of one-hole contexts from the structure of $F$. As our choice of notation $\partial F$ already reveals, the rules for constructing one-hole contexts of sums, products and compositions are exactly Leibniz' rules for differentiation.

ワンホールコンテキスト		解説
$(\partial {\mathit {Const_{A}}})\,X$	$=\,0$	$A={\mathit {Const_{A}}}\,X$の中に$X$は存在しない。つまりワンホールコンテキストの型は空でなければならない。There is no $X$ in $A={\mathit {Const_{A}}}\,X$, so the type of its one-hole contexts must be empty.
$(\partial {\mathit {Id}})\,X$	$=\,1$	$X={\mathit {Id}}\,X$の中に$X$の要素が一つだけ存在する場所がある。$X$を一つ削除すると、結果は$X$を残さない。削除できる場所が一つだけ存在するから、${\mathit {Id}}\,X$はまさにワンホールコンテキストの一つである。したがって、ワンホールコンテキストの型は単一の要素からなるシングルトン型である。There is only one position for items $X$ in $X={\mathit {Id}}\,X$. Removing one $X$ leaves no $X$ in the result. And as there is only one position we can remove it from, there is exactly one one-hole context for ${\mathit {Id}}\,X$. Thus, the type of one-hole contexts is the singleton type.
$\partial (F+G)$	$=\partial F+\partial G$	$F+G$型は、型$F$か型$G$のいずれかであるとすると、ワンホールコンテキストもまた$\partial F$か$\partial G$である。As an element of type $F+G$ is either of type $F$ or of type $G$, a one-hole context is also either $\partial F$ or $\partial G$.
$\partial (F\times G)$	$=F\times \partial G+\partial F\times G$	二つの型の組のワンホールコンテキストは、第一または、第二成分のいずれかが穴である。 The hole in a one-hole context of a pair is either in the first or in the second component.
$\partial (F\circ G)$	$=(\partial F\circ G)\times \partial G$	連鎖律(Chain rule)：合成の穴は囲んでいる構造に穴を開け、そこに密閉構造を当てはめることによって生じる。 Chain rule. The hole in a composition arises by making a hole in the enclosing structure and fitting the enclosed structure in.

もちろん、穴を埋める関数plugの型は$(\partial F\,X)\times X\to F\,X$を持つ。

Of course, the function plug that fills a hole has the type $(\partial F\,X)\times X\to F\,X$.

これまでのところ、$\partial$という構文は異なる関手を表している。すなわち、一つの引数を持つ型関数の種(kind)である。しかし、計算のためにもう少し適した$\partial _{X}$という表記法もある。添え字は微分したい変数を表している。一般には

$(\partial F)\,X=\partial _{X}(F\,X)$

である。例を挙げると以下のようになる。

$\partial ({\mathit {Id}}\times {\mathit {Id}})\,X=\partial _{X}(X\times X)=1\times X+X\times 1\cong 2\times X$

もちろん、$\partial _{X}$は単にポイントワイズで、$\partial$はポイントフリースタイルである。

So far, the syntax $\partial$ denotes the differentiation of functors, i.e. of a kind of type functions with one argument. But there is also a handy expression oriented notation $\partial _{X}$ slightly more suitable for calculation. The subscript indicates the variable with respect to which we want to differentiate. In general, we have

$(\partial F)\,X=\partial _{X}(F\,X)$

An example is

$\partial ({\mathit {Id}}\times {\mathit {Id}})\,X=\partial _{X}(X\times X)=1\times X+X\times 1\cong 2\times X$

Of course, $\partial _{X}$ is just point-wise whereas $\partial$ is point-free style.

演習

いくつかの規則をポイントワイズスタイルに書き換えよ。例えば、乗法則の左辺は次のようになる。$\partial _{X}(F\,X\times G\,X)=\dots$Rewrite some rules in point-wise style. For example, the left hand side of the product rule becomes $\partial _{X}(F\,X\times G\,X)=\dots$. ワンホールコンテキストに慣れるために、因数をちょうど$n$回掛けた$X^{n}:=X\times X\times \dots \times X$を微分し、結果と公式が一致すること確かめよ。To get familiar with one-hole contexts, differentiate the product $X^{n}:=X\times X\times \dots \times X$ of exactly $n$ factors formally and convince yourself that the result is indeed the corresponding one-hole context. もちろん、ワンホールコンテキストは$X$の値を後ろに差し込むことが出来ない場合は役に立たない。5つの規則に対応するplug関数を書け。Of course, one-hole contexts are useless if we cannot plug values of type $X$ back into them. Write the plug functions corresponding to the five rules. 2変数の場合の連鎖律を定式化し、それがワンホールコンテキストをもたらすことを証明せよ。これは$(X,Y)$の組における通常の関手を双関手(bifunctor)$F\,X\,Y$として見れば出来るだろう。もちろん、ポイントフリースタイルでの双関手の偏微分のために便利な記法が必要になるかもしれない。Formulate the chain rule for two variables and prove that it yields one-hole contexts. You can do this by viewing a bifunctor $F\,X\,Y$ as an normal functor in the pair $(X,Y)$. Of course, you may need a handy notation for partial derivatives of bifunctors in point-free style.

微分を介したZipper

上記の規則で再帰的データ型$\mu F:=\mu X.\,F\,X$のzipperを構築することができる。ここで$F$は多項式関手(polynomial functor)である。Zipperは特定のサブツリーに焦点を移す。すなわち、大きな木構造の内側は同じ種類の$\mu F$型のサブ構造である。前章のように、焦点を向けたい場所のサブツリーと糸、これはサブツリーが格納されているコンテキストだが、この二つによって表現することが出来る。

${\mathit {Zipper}}_{F}=\mu F\times {\mathit {Context}}_{F}$

The above rules enable us to construct zippers for recursive data types $\mu F:=\mu X.\,F\,X$ where $F$ is a polynomial functor. A zipper is a focus on a particular subtree, i.e. substructure of type $\mu F$ inside a large tree of the same type. As in the previous chapter, it can be represented by the subtree we want to focus at and the thread, that is the context in which the subtree resides

${\mathit {Zipper}}_{F}=\mu F\times {\mathit {Context}}_{F}$.

今、コンテキストは$F\,\mu F$の中から選択した特定のサブツリー$\mu F$の各手順である。したがって、選ばなかったサブツリーはワンホールコンテキスト$\partial F\,(\mu F)$と一緒に回収される。このコンテキストの穴は選択したサブツリーから削除しながら帰ってくる。置くことも一緒で、

${\mathit {Context}}_{F}={\mathit {List}}\,(\partial F\,(\mu F))$

Now, the context is a series of steps each of which chooses a particular subtree $\mu F$ among those in $F\,\mu F$. Thus, the unchosen subtrees are collected together by the one-hole context $\partial F\,(\mu F)$. The hole of this context comes from removing the subtree we've chosen to enter. Putting things together, we have

${\mathit {Context}}_{F}={\mathit {List}}\,(\partial F\,(\mu F))$。

を得る。または同じ事だが

or equivalently

${\mathit {Context}}_{F}=1+\partial F\,(\mu F)\times {\mathit {Context}}_{F}$。

具体的な計算過程がどのようになるかを説明するために、体系的に迷宮データ型のzipperを構築しよう。

To illustrate how a concrete calculation proceeds, let's systematically construct the zipper for our labyrinth data type

data Node a = DeadEnd a
            | Passage a (Node a)
            | Fork a (Node a) (Node a)

この再帰型は次のような不動点である。 This recursive type is the fixed point

${\mathit {Node}}\,A=\mu X.\,{\mathit {NodeF}}_{A}\,X$

この関手は次のようなものだ。 of the functor

${\mathit {NodeF}}_{A}\,X=A+A\times X+A\times X\times X$

言い換えると、 In other words, we have

${\mathit {Node}}\,A\cong {\mathit {NodeF}}_{A}\,({\mathit {Node}}\,A)\cong A+A\times {\mathit {Node}}\,A+A\times {\mathit {Node}}\,A\times {\mathit {Node}}\,A$.

微分で読むと、 The derivative reads

$\partial _{X}({\mathit {NodeF}}_{A}\,X)\cong A+2\times A\times X$

そして次を得る。 and we get

$\partial {\mathit {NodeF}}_{A}\,({\mathit {Node}}\,A)\cong A+2\times A\times {\mathit {Node}}\,A$.

したがって、コンテキストで読むと、

Thus, the context reads

${\mathit {Context}}_{\mathit {NodeF}}\cong {\mathit {List}}\,(\partial {\mathit {NodeF}}_{A}\,({\mathit {Node}}\,A))\cong {\mathit {List}}\,(A+2\times A\times ({\mathit {Node}}\,A))$.

前章のものと比べてみると、

Comparing with

data Branch a  = KeepStraightOn a
               | TurnLeft  a (Node a)
               | TurnRight a (Node a)
type Thread a  = [Branch a]

期待通り両者が全く同じものであることがわかるだろう！

we see that both are exactly the same as expected!

演習
三分木のzipperを微分の観点でやり直せ。Redo the zipper for a ternary tree, but with differentiation this time. リストのzipperを構築せよ。Construct the zipper for a list. 前回の演習に関係した華麗な質問：リストとスタックの違いとは何だろうか？Rhetorical question concerning the previous exercise: what's the difference between a list and a stack?

不動点の微分

データ型には和と積以上のもの、微積分には直接対応しない不動点オペレータも存在する。その結果、先の表は微分の規則が欠落している。要するに、不動点$\mu F\,X=\mu Y.\,F\,X\,Y$はどのように微分すればいいだろうか。

There is more to data types than sums and products, we also have a fixed point operator with no direct correspondence in calculus. Consequently, the table is missing a rule of differentiation, namely how to differentiate fixed points $\mu F\,X=\mu Y.\,F\,X\,Y$:

$\partial _{X}(\mu F\,X)={?}$

二変数の連鎖律を定式化するのは演習問題に任せる。代わりに、具体例として${\mathit {Node}}\,A$型を計算しよう。

As its formulation involves the chain rule in two variables, we delegate it to the exercises. Instead, we will calculate it for our concrete example type ${\mathit {Node}}\,A$:

${\begin{matrix}\partial _{A}({\mathit {Node}}\,A)&=&\partial _{A}(A+A\times {\mathit {Node}}\,A+A\times {\mathit {Node}}\,A\times {\mathit {Node}}\,A)\\&\cong &1+{\mathit {Node}}\,A+{\mathit {Node}}\,A\times {\mathit {Node}}\,A\\&&+\partial _{A}({\mathit {Node}}\,A)\times (A+2\times A\times {\mathit {Node}}\,A).\end{matrix}}$

もちろん、$\partial _{A}({\mathit {Node}}\,A)$をさらに展開しても意味はないが、右辺の項を

$T\,A=1+{\mathit {Node}}\,A+{\mathit {Node}}\,A\times {\mathit {Node}}\,A$ $S\,A=A+2\times A\times {\mathit {Node}}\,A$

とそれぞれ置くと、これを不動点の等式として見ることが出来、次の式に辿り着く。

$\partial _{A}({\mathit {Node}}\,A)=\mu X.\,T\,A+S\,A\times X$

Of course, expanding $\partial _{A}({\mathit {Node}}\,A)$ further is of no use, but we can see this as a fixed point equation and arrive at

$\partial _{A}({\mathit {Node}}\,A)=\mu X.\,T\,A+S\,A\times X$

with the abbreviations

$T\,A=1+{\mathit {Node}}\,A+{\mathit {Node}}\,A\times {\mathit {Node}}\,A$

and,

$S\,A=A+2\times A\times {\mathit {Node}}\,A$

再帰型は要素の型$S\,A$とのリストのようなもので、空のリストは基本ケースの$T\,A$型で置き換えただけだ。しかし、有限のリストを与えると、$1$と基本ケースを置き換えることが出来、リストから$T\,A$を引っ張り出す。

The recursive type is like a list with element types $S\,A$, only that the empty list is replaced by a base case of type $T\,A$. But given that the list is finite, we can replace the base case with $1$ and pull $T\,A$ out of the list:

$\partial _{A}({\mathit {Node}}\,A)\cong T\,A\times (\mu X.\,1+S\,A\times X)=T\,A\times {\mathit {List}}\,(S\,A)$

最後の段落で導出したzipperと比較すると、リスト型はコンテキストであることが解る。

Comparing with the zipper we derived in the last paragraph, we see that the list type is our context

${\mathit {List}}\,(S\,A)\cong {\mathit {Context}}_{\mathit {NodeF}}$

そしてこれは and that

$A\times T\,A\cong {\mathit {Node}}\,A$

であり、最後に、以下を得る。 In the end, we have

${\mathit {Zipper}}_{\mathit {NodeF}}\cong \partial _{A}({\mathit {Node}}\,A)\times A$

したがって、この具体例${\mathit {Node}}\,A$を$A$について微分すると$A$にzipperをもたらすのだ！

Thus, differentiating our concrete example ${\mathit {Node}}\,A$ with respect to $A$ yields the zipper up to an $A$!

演習
不動点の微分を２変数の連鎖律を使って定式化せよ。Use the chain rule in two variables to formulate a rule for the differentiation of a fixed point. 不動点には帰納的不動点(inductive fixed points: $\mu$)と余帰納的不動点(coinductive fixed points: $\nu$)があることを知っているかもしれない。帰納的不動点の規則は何だろうか？Maybe you know that there are inductive ($\mu$) and coinductive fixed points ($\nu$). What's the rule for coinductive fixed points?

引数の関数に関する微分

ワンホールコンテキストの型を見つけるときの一つはd f(x)/d xを行うことである。それは、d f(x)/d g(x)のような式を完全に解くことが可能だ。 例えば、d x^4 / d x^2は2x^2を与えて解くと、4つのタプルの2ホールコンテキストである。導関数は次のようなものである。 let u=x^2 d x^4 / d x^2 = d u^2 /d u = 2u = 2 x^2 .

When finding the type of a one-hole context one does d f(x)/d x. It is entirely possible to solve expressions like d f(x)/d g(x). For example, solving d x^4 / d x^2 gives 2x^2 , a two-hole context of a 4-tuple. The derivation is as follows

u=x^2と置くと、 d x^4 / d x^2 = d u^2 /d u = 2u = 2 x^2 .

Zipper vs コンテキスト

しかし一般的には、zipperとワンホールコンテキストは異なるもので表される。zipperは勝手なサブツリーの焦点である一方、ワンホールコンテキストは型構築子の引数にだけ焦点を当てることができる。次のデータ型を例に取ろう。

In general however, zippers and one-hole contexts denote different things. The zipper is a focus on arbitrary subtrees whereas a one-hole context can only focus on the argument of a type constructor. Take for example the data type

 data Tree a = Leaf a | Bin (Tree a) (Tree a)

ここで不動点は次の通りである。 which is the fixed point

${\mathit {Tree}}\,A=\mu X.\,A+X\times X$.

zipperはサブツリーのトップであるBinやLeafに焦点を当てることが出来るが、${\mathit {Tree}}\,A$のワンホールコンテキストの穴はLeafだけに焦点を当てるだろう。なぜなら、これは$A$型の要素が存在しているからだ。${\mathit {Node}}\,A$の導関数はサブツリーの全てのトップが常に$A$で飾られているので、zipperであることが判明する。

The zipper can focus on subtrees whose top is Bin or Leaf but the hole of one-hole context of ${\mathit {Tree}}\,A$ may only focus a Leafs because this is where the items of type $A$ reside. The derivative of ${\mathit {Node}}\,A$ only turned out to be the zipper because every top of a subtree is always decorated with an $A$.

演習

驚いたことに、$\partial _{A}({\mathit {Tree}}\,A)\times A$と${\mathit {Tree}}\,A$のzipperは再び同じ型になることが判明した。計算することは容易いが、なぜこのようになるか理由を与えることができるだろうか？Surprisingly, $\partial _{A}({\mathit {Tree}}\,A)\times A$ and the zipper for ${\mathit {Tree}}\,A$ again turn out to be the same type. Doing the calculation is not difficult but can you give a reason why this has to be the case? $\mu F$のzipperは補助変数$Y$導入し、それに関して$\mu X.\,Y\times F\,X$を微分して$Y=1$で再び置き換えて得ることが出来ることを証明せよ。なぜこのようなことができるのだろうか？Prove that the zipper construction for $\mu F$ can be obtained by introducing an auxiliary variable $Y$, differentiating $\mu X.\,Y\times F\,X$ with respect to it and re-substituting $Y=1$. Why does this work? zipperとは異なるワンホールコンテキスト$G\,A$型を見つけよ。Find a type $G\,A$ whose zipper is different from the one-hole context.

帰結

離散的な状況の中で現れた計算からの規則でどうしてこのようなことが起こるのか、という問いでこのセクションを閉じよう。現在のところ、この答えを知るものはいない。しかし少なくとも、”一度限り”という意味での線形には離散的な概念が存在する。ワンホールコンテキストの穴に$X$を差し込む関数の主な特徴は、要素が一度限りしか使われないという事実、すなわち線形ということだ。我々は次のような型を持つ差し込み写像として考えることが出来る。

$\partial _{X}F\,X\to (X\multimap F\,X)$

ここで、$A\multimap B$は、その引数を無視したり複製したりしない線形論理としての線形関数(liner function)を表している。ある意味では、ワンホールコンテキストは関数空間$X\multimap F\,X$を表現したもので、これは$X\to F\,X$に線形近似されていると考えることが出来る。

We close this section by asking how it may happen that rules from calculus appear in a discrete setting. Currently, nobody knows. But at least, there is a discrete notion of linear, namely in the sense of "exactly once". The key feature of the function that plugs an item of type $X$ into the hole of a one-hole context is the fact that the item is used exactly once, i.e. linearly. We may think of the plugging map as having type

$\partial _{X}F\,X\to (X\multimap F\,X)$

where $A\multimap B$ denotes a linear function, one that does not duplicate or ignore its argument, as in linear logic. In a sense, the one-hole context is a representation of the function space $X\multimap F\,X$, which can be thought of being a linear approximation to $X\to F\,X$.

Notes

解説[作成]

See Also

• Zipper on the haskell.org wiki
• Generic Zipper and its applications
• Zipper-based file server/OS
• Scrap Your Zippers: A Generic Zipper for Heterogeneous Types