この解説書は翻訳であり、元記事の国籍は複数の国に及び、フランス版ウィキブックスの記事『Hydrodynamique des fluides parfaits』およびイングリッシュ版の記事『Fluid Mechanics/Fluid Properties』などを引用元とする、翻訳の文書です。
- 協力者の募集
加筆・訂正や翻訳(和訳)を行ってくれる協力者をお待ちしています。日本版の内容は暫定的な物です。
現時点では、翻訳がメインですが、和訳に意訳が含まれるところもあり、元記事と内容が異なる場合もありますので、ご容赦ください。
また将来的には、日本版の独自の記述を追加したりなど、日本版の独自化があるかもしれません。
また、フランス版以外やイングリッシュ版以外からの、その他の国のウィキブックスなどからの翻訳和訳も、記事内容に追加するかもしれません。
執筆の方針についての議論などは、詳しくは「議論」ページを利用したいと思います。
時間の間隔を 、 通過する体積を
、 通過する体積を  とすると、体積流量
とすると、体積流量 は次式で与えられる。
は次式で与えられる。

で体積流量(Débit volumique)は、与えられる。
次の図では、
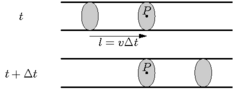
我々は、体積  を見て, 影付きの二つのセクション間,
を見て, 影付きの二つのセクション間,
 の点を通過する、
の点を通過する、  、と
、と  時間の間 .この時点で
ポイント流体速度は
時間の間 .この時点で
ポイント流体速度は  . したがって, スペースの長さは次式で与えられる。
. したがって, スペースの長さは次式で与えられる。 . 故に
. 故に
 , とともに
, とともに  流れのセクション、
流れのセクション、

だった。
流体が非圧縮性(ひ あっしゅくせい)のときは, 体積が流れを通じて保存されている。したがって、いずれかの
流れのポイントで、同じ体積を費やしている  同時に
同時に  . 同時に
体積流量の保全. すなわち、すべての点において、
. 同時に
体積流量の保全. すなわち、すべての点において、  と
と  流れがあった
流れがあった


定義 :質量流量(しつりょう りゅうりょう,Débit massique)とは、その時点で毎秒あたりに通過する流体の質量である。
時間のため の場合 彼は質量
の場合 彼は質量  をついやし、次に質量流量
をついやし、次に質量流量  (または
(または
 ) とによって与え
) とによって与え

密度を とすれば、密度は以下のように定義される。
とすれば、密度は以下のように定義される。

流体が均一であると仮定すると、密度の式は以下のように簡略化することができる。

体積流量は質量流量に換算することができます。  なので
なので

同様に、方程式の式を使用して:dv2 を我々は得る

非圧縮性流体の場合は、質量流量と同じ特性に体積流量を求められる。 これは、すべてのポイントであることを意味  と
と  流れがあった
流れがあった

非圧縮性流体の流れの一部である

流れの保全によると、次のようになる。
 で、あった。
で、あった。
など  その後
その後  . これは直感的です. 同じレートでを取得するには
小さいセクション, 増加を早める必要があります.
. これは直感的です. 同じレートでを取得するには
小さいセクション, 増加を早める必要があります.
これは、流れの上のセクションでは、より高い速度を引き締めることは注目に値する.
次のような状況を考える:

非圧縮性流体の場合、それがあった:  .
.
我々はこの結果を一般化することができます。流路の接点では、流入の和(または体積質量が)流出の和に等しい。
非圧縮性流体の連続的な流れについては2点間であった  と
と  単一の現在の流線:
単一の現在の流線:

とともに
*  は圧力で、点
は圧力で、点 で。
*
で。
*  流体の密度
*
流体の密度
*  重力加速度
*
重力加速度
*  標高で、点
標高で、点  で。
*
で。
*  速度で、 点
速度で、 点  で。
*
で。
*  流れの外部アクチュエータ (ポンプ,
タービン,…).
アクチュエータは、流れを供給する場合 (ポンプ,…) その後
流れの外部アクチュエータ (ポンプ,
タービン,…).
アクチュエータは、流れを供給する場合 (ポンプ,…) その後  .
アクチュエータは、力を受けた場合 (タービン,…) その後
.
アクチュエータは、力を受けた場合 (タービン,…) その後  .
*
.
*  体積流量
体積流量
このような式が、ベルヌーイの方程式(L'équation de Bernoulli)である。
静水圧の場合、速度はゼロである ( ) アクチュエータはありません (
) アクチュエータはありません ( ) だからベルヌーイ式に従って式を与えるのだった。
) だからベルヌーイ式に従って式を与えるのだった。

一つは、その後、流体静力学の基本的な関係を見つけた (したがって、ベルヌーイの定理の特殊なケースである).

下部にあるバルブでタンクを空には、このいずれかで実行され. ポイントが配置されている
 (
( ) タンクの自由表面との時点で
) タンクの自由表面との時点で  表面上
タップを残しジェット(
表面上
タップを残しジェット( ).
参照高度をタンク底として(故に
).
参照高度をタンク底として(故に  と
と  ).
点の間にはアクチュエータがありません
).
点の間にはアクチュエータがありません  と
と  (
( ).
).
ベルヌーイ方程式になる

流体は非圧縮性である点間 と
と  との点間での体積流量の保全があります.
または
との点間での体積流量の保全があります.
または

しかし、セクション  点
点  (通常)バルブのセクションよりもはるかに大きい (
(通常)バルブのセクションよりもはるかに大きい ( ).
もし
).
もし  . その後、我々は言葉を無視することができます
. その後、我々は言葉を無視することができます  方程式式でeq:tori1.
方程式式でeq:tori1.
その後, 簡素化した後  と再編
と再編

この式は、(このセクションのすべての方程式のように)知っているされていません
しかし、あなたはそれを見つけるために使用されているデモンストレーションおよび仮定を知っている必要があります。
私たちは、サイズにポンプを試す  高さにタンクから水を供給する
高さにタンクから水を供給する 
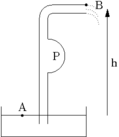
前節と同様に、我々  ,
,  と
と  . 通常は、流体のセクションに同じ近似を行うことができます
. 通常は、流体のセクションに同じ近似を行うことができます  と
と  , だから私たちは無視することができます
, だから私たちは無視することができます  . ベルヌーイの式 になる (簡素化圧力後)
. ベルヌーイの式 になる (簡素化圧力後)

質量流量の関数としてこの式を書き換えることが可能である  . その後、我々
. その後、我々

(Effet Venturi)
引き締めと流れです
ベルヌーイ方程式で, 等しい高度だった
( ) およびno
作動装置 (
) およびno
作動装置 ( ). したがって、我々は得る
). したがって、我々は得る

使い方 当式:速度が得られる

誤算 : 自乗に比べてSb/Saを置くべき
など  だった
だった  または
または  . これは、より多くの流れが収縮し、圧力が低下することを示している。
. これは、より多くの流れが収縮し、圧力が低下することを示している。
短所 - 直感的な結果もベンチュリーのパラドックスと呼ばれています。この効果は、しかし、本物である
これは、特に嵐の間に屋根を引き裂くための責任があるものです
またはそうでなければ、航空機の飛行の原理である。
粘度(「ねんど」。記号はμ、ギリシャ文字のμで表される、英:Viscosity)とは、物性値である。
粘度は流体に固有の値であり、それは流体の流れの抵抗力を測定する。
流体の特性にもかかわらず、流体が動いているときにのみ、その効果が理解される。
異なる要素が異なる速度で移動すると、各要素がそれと一緒に、その隣接要素を引きずろうとします。したがって、せん断応力は、異なる速度の流体要素の間に発生します。
 層流せん断流における速度勾配
層流せん断流における速度勾配
せん断応力と速度場の関係は、アイザック·ニュートンによって研究され、彼はせん断応力が速度勾配に正比例していることを提案した。
 比例定数は、動的粘性係数(coefficient of dynamic viscosity)と呼ばれています。
比例定数は、動的粘性係数(coefficient of dynamic viscosity)と呼ばれています。
動粘度(kinematic viscosity)として知られている別の係数、 ( , ギリシア文字の「ニュー」) の定義は、動的粘度と密度の比として定義される。
, ギリシア文字の「ニュー」) の定義は、動的粘度と密度の比として定義される。
すなわち、
それは、流体の流れに対する抵抗を定量化する流体の特性である。
無次元数(Dimensionless parameters)は、分析を単純化し、単位を参照することなく、物理的な状況を記述するために使用される。無次元量は、それに関連付けられた物理的な単位を持っていません。
レイノルズ数(Reynolds Number)は、(オズボーン=レイノルズ、1842年から1912年後)は、流体の流れの研究で使用されている。これは慣性と粘性の効果の相対的な強さを比較します。
レイノルズ数の値は以下のように定義される:

ここで ρ(rho) は密度であり, μ(mu) は粘度(ねんど)であり, V は流れの代表的な速度であり, そして L は代表長さである。
| 例0.1:平板フローのレイノルズ数
|
| 温度293K、密度1.225 kg m-3 では、エアーは1m s-1で平板を過ぎて流れている。平板の前縁から1メートル下流のレイノルズ数は何ですか?
|
| 空気の絶対粘度は1.8 × 10-5 N s m-2である .

|
くわえて, 変数 ν(nu) は 動粘度 (どうねんど)と定義される.
低い Re はクリープ流れ(creeping flow)を示し, 中間の Re は 層流 (そうりゅう、laminar flow)であり, 高い Re は 乱流 (らんりゅう、turbulent flow)を示す。
レイノルズ数は、異なる流れの条件を考慮して変換することができる。例えば、パイプ内の流れのためのレイノルズ数は次式で表され

ここで u は パイプ内にある流体の流速の平均であり 、そして d は パイプの内径.

















































































