高等学校化学I/化学結合
イオン
[編集]イオン
[編集]イオンと電解
[編集]塩化ナトリウムNaClを水に溶かして塩化ナトリウム水溶液をつくると、ナトリウムイオンNa+と塩素イオンCl-のような、正負の電荷をもった粒子に分かれる。このように、電荷を持った粒子をイオン(ion)という。
このときに生ずる、正の電荷を持つ粒子を陽イオン(cation)という。いっぽう、負の電荷を持つ粒子を陰イオン(anion)という。
塩化ナトリウム水溶液の場合、 Na+ が陽イオンであり、Cl- が陰イオンである。
塩化ナトリウム水溶液は、電気を通す。その仕組みは、陽イオンと陰イオンが、塩化ナトリウム水溶液中では、ほぼ自由に動けるからである。
また、このように、溶解の際に、物質がイオンに分かれる現象を電離(でんり, ionizasion)という。そして、水に解けて電離する物質を電解質(でんかいしつ, electrolyte)という。
いっぽう、アルコールやグルコース(砂糖)の溶液は、水に溶けても電解しない。このアルコールなどのように、水に溶けても電解しない物質を非電解質(ひでんかいしつ)という。グルコース水溶液は、電気を通さない。

イオンと電子配置
[編集]ナトリウム原子 Na は、価電子を1個放出すると、電子配置が、希ガスのネオン Ne の電子配置と同じになり、安定する。(ナトリウムの原子番号は11であるため、K殻に2個、L殻に8個、M殻に1個の電子が含まれる。)なのでナトリウムイオン Na+ のように、1価の陽イオンになりやすいのである。
いっぽう、塩素原子 Cl は、価電子を1個、外部から受け取ると、電子配置が、希ガスの電子配置と同じになる。
-
ナトリウム
-
塩素
同様に、マグネシウム Mg は、価電子2個を失いやすく、 Mg2+ になりやすい。同様に、アルミニウム Al は、価電子3個を失いやすく、 Al3+ になりやすい。
価電子が1〜3個など、価電子の少ない原子は、電子を失って陽イオンになりやすい。逆に、価電子が6〜7個など、価電子の多い原子は、電子を受け取って陰イオンになりやすい。
イオンができる際に、放出したり受け取ったりと、やりとりした電子の数を、そのイオンの価数(かすう、charge number)という。価数が1のときそのイオンは1価であるといい、同様に価数が2のときそのイオンは2価であり、価数が3なら3価、・・・と数える。電子の電荷は-eであるが、ここでは、電子一つを基準にしていることに注意。
原子記号では、価数は右上に書く。
例
このように、元素記号と、その右上に価数と正負の符号で表記する方法を、イオン式(ion fomula)という。
イオンの化学式をあらわすには、イオン式を用いる。
また、塩素Clの価数のように、1価の場合は、数字の1を省略する。
Na+ や Cl- や Mg2+のように、原子一粒が電子を受け取ったり渡したりしてイオンになったものを単原子イオン(たんげんしイオン、monoatomic ion )という。
アンモニウムイオン NH4+ や水酸化物イオンOH-のように、二個以上の原子が結合した原子団に、電子が結合したり取れたりしてできたイオンを多原子イオン(たげんしイオン、polyatomic ion)という。
なお一般的に、陽イオンは「~イオン」、陰イオンは「~化物イオン」と呼ばれる場合が多い。また、多原子イオンであれば、それがイオンになる前の分子の名前に「~イオン」や「~化物イオン」と付けて呼ばれることが多い。上述の例で言うなら、アンモニアのイオンはアンモニウムイオンである。
| 価数 | 陽イオン | イオン式 | 価数 | 陰イオン | イオン式 |
|---|---|---|---|---|---|
| 1価 | 水素イオン | 1価 | 塩化物イオン | ||
| ナトリウムイオン | 水酸化物イオン | ||||
| カリウムイオン | 硝酸イオン | ||||
| 銀イオン | 炭酸水素イオン | ||||
| アンモニウムイオン | |||||
| 2価 | マグネシウムイオン | 2価 | 酸化物イオン | ||
| カルシウムイオン | 硫化物イオン | ||||
| 亜鉛イオン | 炭酸イオン | ||||
| 鉄イオン | 硫化物イオン | ||||
| 銅イオン | |||||
| 3価 | アルミニウムイオン | 3価 | リン酸イオン | ||
| 鉄イオン | |||||
| クロムイオン |
*ただし上の表にあるように鉄には価数が2個のものと3個のものがあり、それぞれ鉄(Ⅱ)イオン、鉄(Ⅲ)イオンともいう。
イオンの生成とエネルギー
[編集]イオン化エネルギー
[編集]原子から最外殻電子1個を取り去って、1価の陽イオンにするのに必要なエネルギーのことをイオン化エネルギー(ionization energy)という。
一般に、イオン化エネルギーの小さい原子ほど、陽イオンになりやすい。
Li、Na、K などのアルカリ金属は、イオン化エネルギーが小さいからこそ陽イオンになりやすいのである。
いっぽう、陰性の強い元素は、イオン化エネルギーが大きい。
また、He、Ne、Ar などの希ガス元素はイオン化エネルギーが非常に大きいので、安定しているのである。
- 一般にイオン化エネルギーは、1mol(単位:モル)あたりのエネルギー(単位: kJ キロジュール)で表す。
※ 単位「mol」(モル)については、のちの単元で習う。もし読者が、高校2年の1学期に初めてここの単元を習ってる段階なら、まだモルについては、気にしなくて良い。
電子親和力
[編集]原子が電子1個を受け取って、1価の陰イオンになるときに放出されるエネルギーのことを電子親和力(でんし しんわりょく、electron affinity、でんし しんわりょく)という。
たとえば塩素Clが電子1を受け取って塩化物イオン Clー になるとき、エネルギーを放出する。
一般に、電子親和力の大きい元素ほど、陰イオンになりやすい。(※ 実教出版、啓林館、東京書籍の教科書などで紹介されている。) このため、電子親和力の大きさは、その元素の陰イオンの安定さを表す・・・、と考えられている(※ 東京書籍の見解)。
F、Cl、Br などのハロゲン原子は電子親和力が非常に大きく、1価の陰イオンになりやすい。
- ※ 日本では慣例的に電子親和「力」というが、じつは物理学の力学でいう「力」(ちから)ではなく、上述のようにエネルギーである。
(発展:) なお、電子親和力の測定方法は、直接の測定が困難なので、おもに光を放つ現象や、あるいは元素に光を照射して元素に吸収させる方法が、原子親和力の測定利用されている。つまり、おもに光の発生や吸収を利用して、電子親和力を測定することが多い。(※ 啓林館の化学基礎の教科書で紹介されている。)
イオン結合
[編集]イオン結合とイオン結晶
[編集]
塩化ナトリウムNaClでは、ナトリウム原子からは価電子の1個を出して陽イオンのナトリウムイオンNa+になっている。塩素原子Clは、ナトリウムから不出された価電子を受取り、陰イオンの塩素イオンCl-になっている。
そして、Na+とCl-が静電気的な引力(クーロン力)で結合している。
NaClの結晶の中では、Na原子の数とCl原子の数は同数であり、つまり1:1の割り合いである。

このように、陽イオンと陰イオンとが静電気的によって結びつく結合のことをイオン結合(ionic bond)という。
一般に、陽性の強い金属元素と(たとえばNaなど)、陰性の強い非金属元素(たとえばClなど)との間に、イオン結合が生じやすい。
一般に、イオン結合の強さは、両方のイオンの価数の積が大きいほど、結合も強い。(「価数」とは、たとえばCa2+ならば「2+」の部分が価数である。)
また,塩化ナトリウムNaClのように、イオン結合でできている結晶のことをイオン結晶(ionic crystal)という。
- 参考
NaCl結晶中の NaClの1単位と、同じ結晶中のべつの NaCl 1単位とは、けっしてイオン結合はしてない。棒などでつつくなどして結晶に外力を加えると、すぐに割れてしまったり壊れたりして、粉末状になってしまうことが多い。外力で割れやすいのは、原子配置が一個でもずれると、同種の電荷のイオンどうしが接近してしまい反発してしまうからである。
また、一般に、イオン結晶は水に溶けやすい。イオン結晶を溶かした水は電気を通す。 水に溶かしていない、固体状の結晶じたいは電気を通さない。ただしイオン結晶を高温にして液体にすると、液体の場合には電気を通す。
融点に関しては、イオン結合をしている物質の融点は高い。
組成式
[編集]イオンからなる物質を化学式であらわすには、陽イオンと陰イオンの数の比率をもっとも簡単な整数比で表した組成式(そせいしき、compositional formula)をもちいる。
たとえば「MgCl2」や「NaCl」のように、あらわす。
たとえば塩化マグネシウムの結晶は、Mg2+とClーが 1:2 の比率で存在しているので、組成式はMgCl2 で表される。
また、「NaCl」のように、個数比が1倍の場合は「1」を省略する。
一般に、イオン結晶は電気的に中性であるので、次の関係式がなりたつ。
- 陽イオンの価数 × 陽イオンの数 = 陰イオンの数 × 陰イオンの数
なぜなら、電気的に中性なら、正電荷の総量と負電荷の総量とは等しいので、上式が成りたつのである。
- イオン結晶の物質例
- 酸化銅 CuO
構成している原子と価数
- Cu2+ と O2ー
- 炭酸カルシウム CaCO3
構成している原子と価数
- Ca2+ と CO32ー
- 硫酸アンモニウム (NH4)2SO4
構成している原子と価数
- NH4+ と SO42ー
- 塩化アルミニウム Al2Cl3
構成している原子と価数
- Al3+ と Clー
分子と共有結合
[編集]H2やO2やH2O のように、いくつかの原子が結びついてできたものが分子(molecular)である。
共有結合
[編集]一般に同種の非金属原子どうしが近づくと(たとえば水素原子どうしが近づくと)、各原子の電子軌道上にある電子を共有することができる。(ただし、共有できる原子数には限りがある。) このような結合を共有結合(covalent bond)という。
- (※ 範囲外 ) なぜ、このような共有結合の現象が起きるかというと、原子規模の物理法則では、物質が狭い場所に押し込められると不安定になり広がろうという不確定性原理とよばれる性質を持つことに由来する。その不確定性原理による広がりの力が、電子どうしの反発力に勝る場合、複数の原子が、電子を共有する現象が起こる。
(不確定性原理の証明は、高校レベルでは困難なので、読者が高校生や中学生なら、ここでは不確定性原理の名前と概略を知っているだけで良い。)
共有結合は、おおむね、以下のような仕組みである。 例として、水素分子での水素原子どうしの結合で説明する。
- 水素原子が近づく。
- それぞれの原子核は、相手原子の価電子(かでんし、valence electron)を引き合う。
- 価電子は、もとの原子を引き付けるから、結局、電子を仲立ちとして、原子核どうしが近づく。原子核どうしが近づいた結果、電子軌道の一部は共有されるので、電子殻の一部が共有される。
- 共有された電子殻の一部では、水素原子の合計2個の価電子は1対になっている。このように価電子が対になったものを電子対(でんしつい,electron pair)という。
ここで注意すべきなのは、電子どうしには引力が生じない、ということである。原子核どうしにも引力は生じない。あくまでも電荷の異なる粒子どうしの、原子核と電子とが電気引力を及ぼしているのである。同種の電荷である原子核どうしには反発力が生じている。同様に、同種の電荷である電子どうしにも反発力が生じている。
このように価電子を仲立ちとして、電子を共有することによって生じる結合を共有結合(covalent bond)という。
対電子は、なにも結合だけではなく、1個の原子の電子殻上でも、価電子が多い場合は、対電子が生じる。 たとえば、L殻の原子では、5個の価電子を持つN原子は1組の電子対をもつ。6個の価電子を持つO原子は2組の電子対をもつ。7個の価電子を持つF原子は3組の電子対をもつ。比較のため、同じL殻のC原子を例に出すと、4個の価電子を持つC原子は0組の電子対をもつ。
電子式
[編集]上図のように、元素記号のまわりに、最外殻電子を・で表した図のような化学式を電子式という。
電子式では、電子をあらわす黒丸は、上下左右の4箇所に配置される。
そして、4個目までの原子は、その4箇所に均等に配分される。
5個目以降の電子が、すでに配置された電子と対(つい)を作り始める。
電子対と不対電子
[編集]
最外殻電子にて、電子の数が多くなると、2個以上の電子で、対(つい)をつくり、その電子は結合に安定な状態になる。この、2個の電子が1対となったものを電子対(でんしつい、electron pair)という。
いっぽう、最外殻電子にて、対を作らない電子のことを不対電子(ふついでんし、unpaired electron)という。
共有結合
[編集]原子どうしの共有結合では、図のように、不対電子どうしが結合にかかわる。

共有結合にて構成される分子にて、原子間で共有されている電子のことを共有電子対という。いっぽう、はじめから電子対になっていて、原子間で共有されていない電子対を非共有電子という。
構造式
[編集]| 分子 | 水素 H2 | 二酸化炭素 CO2 | 窒素 NH3 |
|---|---|---|---|
| 電子式 |  |
 |

|
| 構造式 |  |
 |

|
水素と水素の結合のように、1組の共有電子対による結合を単結合(たんけつごう)という。
構造式では、共有電子対の1組(つまり図中の「:」)は1本の棒線で表される。たとえば水素分子の構造式は
- HーH
となる。棒線の1本あたり、1組の共有電子対を表している。 なお、このような共有電子対を表す線を価標(かひょう,bond)という。
2対の共有電子対による共有結合を二重結合(double bond)という。3対の共有電子対による共有結合を三重結合(triple bond)という。
二重結合の価標は2本の棒線(つまり「=」)で表される。三重結合の価標は3本の棒線(「≡」)で表せる。
分子式、電子式、組成式、構造式などをまとめて化学式(かがくしき、chemical formula)という。
- 原子価
構造式において、1個の原子から出ている価標の数を原子価(げんしか、valency)という。
- 水素Hの原子価は1である。
- 塩素Clの原子価は1である。
- 酸素Oの原子価は2である。
- 炭素Cの原子価は4である。
- 窒素Nの原子価は3である。
原子価は、その元素がもつ不対原子の数にも相当する。
- (整理中)
3個の不対電子を持つ窒素原子Nは、水素原子Hと結合すれば、アンモニアNH3 を作ることができる。
分子の形
[編集]構造式は、かならずしも、分子の実際の形とは一致するとは限らない。
(※ 編集者へ: 下の図表を完成させてください。)
| 分子 | 電子式 | 構造式 | 分子の形 | |
|---|---|---|---|---|
| 水素 H2 |
 |
 |
||
| 水 H2O |
 |
 |
 |
 折れ線型 |
| メタン CH4 |
 |
 |
 |
 正四面体型 |
| アンモニア NH3 |
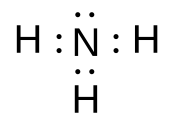 |
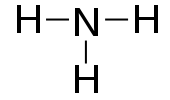 |
 |
 三角すい型 |
| 二酸化炭素 CO2 |
 |
 |
 |
直線型 |
| 窒素 N2 |
 |
 |
 |
|
| エチレン C2H4 |
C2H4の電子式 |  |
 |
 平面構造 |
実は、タングステンやクロム、レニウムでは、四重結合や五重結合、六重結合があることが、報告されている。
検定教科書に「四重結合が無い」と明言されないのは、タングステンなどの事情があるからだろう。
ただし、炭素や酸素、窒素などでは、四重結合は無い。高校で習う多くの元素で、四重結合以上の結合は無い。四重結合以上が無い理由について、いろいろな仮説が提案されているが、それらのどの仮説でも、よく使われる前提として、われわれの空間が三次元であることが、説明に使われることが多い。
(※ この話題は、高度に専門的すぎるため、絶対に入試には出ないだろう。なので高校生は、「化学の多重結合は、原則的に三重結合まで」と思っても良い。)
ちなみに、タングステンやクロム、レニウムはすべて金属である。つまり、金属でしか、四重結合以上は見つかっていない。(少なくとも西暦2018年の時点では。)
上記3つ以外の、鉄や銅や金(きん)などの金属では、四重結合以上は見つかっていない。
配位結合
[編集]配位結合
[編集]
アンモニアNH3を水や濃塩酸HClと反応させるとアンモニウムイオンNH4+が生じる。 これはアンモニアの非共有電子対に、水素イオンが吸引された結果である。水素イオンは価電子を放出して正電荷になっているので、電子に引きつけられる。 このように非共有電子対に、価電子が空のイオンが吸引されてできる結合を配位結合(はいい けつごう ,coordinate bond)という。
NH4+の結合について、アンモニウムイオンNH4+の持つ結合N-Hの4個の結合は、4個とも同等であり、配位結合したあとは区別できない。 このような理由から、配位結合は共有結合の一種と見なされる。
- オキソニウムイオン
水H2Oや、希塩酸などの酸性溶液では、少しだけイオン化をしていて、H3O+とOH-とにイオン化をしている。このH3O+は、H2OにHが配意した配位結合である。このH3O+をオキソニウムイオン(oxonium ion)という。
錯イオン
[編集]| 配位子 | 名称 |
|---|---|
| NH3 | アンミン |
| H2O | アクア |
| CN | シアノ / シアニド |
| OHー | ヒドロキシド |
| Clー | クロロ / クロリド |
金属イオンが中心となって、その金属の周囲に陰イオン(Clー や OHー など)や分子が配位結合をすることで錯イオン(さくイオン、complex ion)を生じる。
たとえば中心金属が銅で、周囲にアンモニア分子が配位すると、錯イオン [Cu(NH3)4]2+ になる。[Cu(NH3)4]2+ の名称は、「テトラアンミン銅(II)イオン」である。
金属イオンに配位結合した分子や陰イオンを配位子(はいいし、ligand)という。
錯イオンにて、中心の金属原子に配位している配位子の個数を配位数という、
極性と電気陰性度
[編集]結合の極性
[編集]
δ+ :わずかに正に帯電している
δー :わずかに負に帯電している
水素分子H2や塩素分子Cl2のように同種の原子の共有結合で出来た結合において、電子対はどちらにも片寄らず、したがって電荷はかたよらない。
いっぽう、塩化水素分子 HCl では、共有電子対は塩素原子に引き寄せられている。その結果、H原子は、すこしばかりの正の電荷 δ+ を帯び、いっぽう、塩素原子は少しばかりの負の電荷 δ- を帯びる。このような電荷のかたよりを結合の極性という。
なおイオン結合は、電荷のかたよりが大きい結合の場合に、電子対が完全に一方の原子に移動したものと考えることができる。
電気陰性度
[編集]
元素の陰性を、数値的に決定することができる。元素の陰性の決定方法には、いくつかの方式が提案されているが、そのうち、有名なものを下記に解説する。(※ 入試には出ないので、高校生は暗記しなくてよい。)
- ポーリングの電気陰性度
ある原子Aの結合からなる二原子分子 AA があったとする。
同様に別のある原子Bの結合からなる二原子分子 BB があったとする。
同種の原子どうし(AAおよびBB)の結合エネルギーは、共有結合のエネルギーみであり、イオン結合のエネルギーは無いはずである。
さて、AとBの結合した分子 AB の結合エネルギー EAB は一般に、AAとBBの平均の結合エネルギーよりも、さらに結合エネルギーが高い。
これは、原子Aと原子Bとの極性の差により、イオン結合のエネルギーが含まれているからである。(※ 上の式は高校範囲外なので覚えなくてよい。)
なら、このイオン結合のエネルギーをもとに、各原子の極性の度合いを実験的に測定できるだろう、と化学者ポーリングなどは考えた。そして、その極性は、2原子のそれぞれの原子の電気陰性度 の差 によって生じると設定した。(※ 上の式は高校範囲外なので覚えなくてよい。)
つまり、同じ原子どうしの結合なら電気陰性度に差は生じず、
となり、よって分極は生じない事になり、実験結果ともあう。
そしてポーリングなどは、フッ素 F の電気陰性度をとりあえず約4.0であると設定して、この設定にあうように比例定数kを掛けた式をつくって、
そして、この式をもとに、さまざまな原子どうしの結合エネルギーの差の実測値をもとに電気陰性度を計算した。(※ 上の式は高校範囲外なので覚えなくてよい。)
このようにして、電気陰性度(でんきいんせいど、electronegativity)の相対値が算出された。電気陰性度はもともと、上記のように2種類の原子からなる二原子分子の分極を説明するために導入された量である。
現在では、電気陰性度は、共有電子対を引きつける力の強さに よく比例する事が 分かっている。(検定教科書では、こちらを定義にしている。つまり、「元素において、共有結合をしている電子対をひきつける力の大きさを、相対的に表したものを電気陰性度という。」のような定義をしている。)
また、こうして電気陰性度を計算した結果、希ガスを除いて周期表の右上にある原子ほど、電気陰性度が高いことが分かった。(検定教科書にも書いてある。)フッ素 F が最大の電気陰性度である。
なおイオン結合は、電気陰性度の差が大きくて、電子対が完全に一方の原子に移動したものと考えることができる。
また、共有結合は、電気陰性度がある程度高くて、さらに電気陰性度が同じくらいの原子との結合で、共有結合が生じるのが一般的である。
- ※ 検定教科書には、じつは「ポーリングの電気陰性度」という用語は登場する。検定教科書にて、電気陰性度の数値のグラフを掲載する際に、「値は、ポーリングの電気陰性度を示した」などのように紹介される場合がある。しかし、上記の計算法までは紹介されてないし、一般的な参考書でも、計算法までは深入りしてないので、計算法までは暗記の必要は無いだろう。
「ポーリングの電気陰性度」の発見後、マリケンが次のことを発見した。
グラフで、縦軸にポーリングの電気陰性度をとり、横軸に原子番号を取るグラフを用意する。
同様に、縦軸にイオン化エネルギー、横軸に原子番号をとったグラフを用意する。
すると、原子番号10以降のほとんどの原子で、グラフでは、イオン化エネルギーの増減と、ポーリングの電気陰性度の増減のようすが、同じように増減することが分かった。
また、同様に、縦軸に電子親和力、横軸に原子番号をとったグラフを用意する。すると、原子番号10以降のほとんどの原子で、グラフでは電子親和力の増減と、ポーリングの電気陰性度の増減のようすが、同じように増減することが分かった。
そこで、化学者マリケンは、原子 A のイオン化エネルギーを IAとし、電子親和力を EAとした際に、縦軸に
をとったグラフが(※ 横軸は原子番号とする)、 が「ポーリングの電気陰性度」と増減が似ていることに、こだわった。(※ 「電子親和力」の単位は(「力」という名に反して)エネルギーが単位である。なので、電子親和力とイオン化エネルギーとは足し算できる。)
また、
を約270で割り算すると、ポーリングの電気陰性度とほぼ同じ値になる。
そして、マリケンなどによって「いっそ、電気陰性度を、イオン化エネルギーと電子親和力を足した値(を2で割った値)として、あらたに定義しよう」というような提案が、なされた。
そして、マリケンはさらに、上述の式にもとづいて、ポーリングとは異なる、あらたな電気陰性度の式を提案した。
つまり、式
で求まる が、マリケンによる新しい電気陰性度の定義である。
このような式による定義を「マリケンの電気陰性度」といい、ポーリングの電気陰性度とは区別する。
ポーリングの電気陰性度とマリケンの電気陰性度は、増減の傾向がよく似た値になる。
ポーリングは1932年に電気陰性度の測定法などを発表しており、マリケンは1934年に上述の計算などを発表している。
- 備考 (教育業界での傾向)
-
- 上述のように「電気陰性度」については、いくつかの定義があり、けっしてひとつの定義には統一されていない。なので、大学入試では、まず出題されないだろう。もし出題されたとしても、本コラム内の式については暗記の必要の無い問題が出るだろう。
- なお、予備校の駿台文庫が出版している参考書で、マリケンの電気陰性度などの式を紹介している。
- 「マリケン」という用語そのものは、啓林館など いくつかの検定教科書でも用語だけは紹介されているが、計算法には深入りしていない。
- 「マリカン」か「マリケン」か、文献によって、 表記のゆれ がある。啓林館の検定教科書では「マリケン」で紹介されているので、本wikibooksでは、「マリケン」表記にした。
- ※ このように「電気陰性度」には、いくつかの定義がある。上述のコラムで紹介した以外にも、さらに別の定義すら提案されている。
- なので、電気陰性度の具体的な計算公式については暗記の必要は無い。
- 高校生の段階では、「フッ素は陰性が高い」とか「ナトリウムは陰性が低い」のように、個別の原子についての具体的な陰性の高低の感覚が分かれば、十分である。
- ※ じつは、化学者のあいだでも、たとえば一酸化炭素 CO のうちの炭素Cと酸素Oのどちらの原子がより陰性なのかとか、分極の方向なのかとか、周期表で近い位置にある原子どうしの結合した分子の分極の方向について意見が分かれている(※ 参考文献: 細矢治夫『はじめての構造化学』、オーム社、平成25年 6月25日 第1版 第1刷、84ページ)。検定教科書に書いてある 分極の向きは、とりあえずの仮定である。
分子の極性
[編集]水素分子H2や塩素分子Cl2のように同種の原子の共有結合で出来た結合において、電子対はどちらにも片寄らず、したがって電荷はかたよらない。 このような電荷の片寄りのない分子を無極性分子(むきょくせいぶんし,nonpolar molecule)という。
いっぽう、塩化水素分子HClでは、塩素に電子は片寄っている。その結果、H原子は、すこしばかりの正の電荷 δ+ を持ち、塩素原子は少しばかりの負の電荷 δ- を持つ。このように分子内に電荷の片寄りのある状態を極性(きょくせい,polarity)と言い、極性の有る分子を極性分子(polar molecule)という。
ニ酸化炭素CO2ではC=Oの結合には極性があるが、分子全体ではO=C=Oが直線上の形状のため、2個のC=O結合の極性同士が反対向きになり、極性が打ち消し合う。したがって、ニ酸化炭素は分子全体では極性をもたない無極性分子である。
| 極性分子 |  (折れ線型) |
 (直線型) |
 (三角すい型) | |
|---|---|---|---|---|
| 無極性分子 |  |
 |
 (直線型) |
 (正四面体型) |
水H2Oは極性分子である。分子全体では折れ線の形になっている。
メタンCH4は無極性分子であり、正四面体の構造をとる。正四面体の4個の頂点に対応する位置に水素原子Hがあり、正四面体の中心に対応する位置に炭素Cがある。
水素結合
[編集]
16族原子のOと結合したH2Oは、同じ16族原子との化合物のH2SやH2Seとくらべて、沸点が特に高い。 17族のFとの化合物のHFは同じ17族原子の HCl などとくらべて沸点が特に高い。 15族のNとの化合物のNH3も同様に、他の同属化合物より沸点が特に高い。 このような現象の仕組みを述べる。

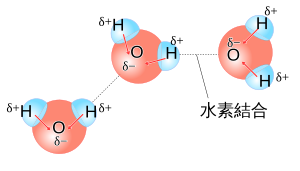
O、F、Nとも電気陰性度の高い元素である。電気陰性度の高い元素(O、F、N)と、水素 H とが、引き合うのである。
例としてHFを解説する。フッ化水素HFはフッ素の電気陰性度が大きく、電子はフッ素Fに吸引される。この結果、水素原子Hは静電荷に帯電する。この分極した水素Hを仲立ちとして、周囲のHF原子のFを吸引する。
これを水素結合(hydrogen bond)という。水素結合は、相手の原子がO、F、Nなどの電気陰性度の高い場合に生じる。
水素結合は、共有結合やイオン結合と比べると、はるかに弱い結合である。しかし、水素結合がファンデルワールス力による結合と比べると、はるかに強い。
結局、水素結合をする物質は、
- H2O
- HF
- NH3
などである。
アンモニア分子どうしも水素結合をする。アンモニア分子のNと、となりのアンモニア分子のHとが、水素結合するからである。

なお、14族元素(CH4など)の水素化合物は無極性なので、他の族と比べても、特に沸点が低い。
ファンデルワールス力
[編集]水素H2やメタンCH4といった無極性の分子でも、冷却していけば液体や個体になる。
これは、無極性分子といえども、分子間に、弱いながらも引力が働いているからである。
極性の有無にかかわらず、分子間の引力のことをファンデルワールス力という。
そして、ファンデルワールス力と水素結合をまとめて分子間力という。

ハロゲンの単体の二原子分子は、分子量が大きくなるほど、沸点も高くなる。こうなる理由は(ハロゲンの単体の二原子分子で、分子量が大きくなるほど、沸点も高くなる理由は)、分子量が大きいほど、分子間力も強くなるからである。(ほぼ同じことだが、理由は「分子量が大きいほど、ファンデルワールス力が強くなるから」と書いてもいい。第一学習社の検定教科書では、ファンデルワールス力で沸点の高くなる理由を説明している。)
分子結晶
[編集]- (※ 編集者: 分子結晶の図を書いてください。CO2の分子結晶。I2(ヨウ素)の分子結晶。)
二酸化炭素を冷却するとドライアイスになるが、図のように二酸化炭素分子が整列した結晶になっている。
二酸化炭素どうしを引きつけてる力は分子間力である。
このように、分子間力によって配列してできた結晶のことを分子結晶(molecular crystal)という。
分子結晶は弱い力であるため、一般に分子結晶は融点・沸点が低く、やわらかい。
また、分子結晶には昇華しやすいものが多い。昇華しやすいものが多い理由も、分子間力が弱いことが理由であろうと一般に考えられている。(検定教科書にそう書いてある。)
二酸化炭素(CO2)、ヨウ素(I2)、ナフタレンが、昇華する物質である。
この昇華する物質である二酸化炭素(CO2)、ヨウ素(I2)、ナフタレンはどれも、無極性分子である。
氷の結晶構造
[編集]- (※ 編集者へ: 図を書いてください。)
氷(こおり)の結晶では、図のように、水1分子あたり水素結合によって4個の分子が引き合ってる。
氷(こおり)は、このように、すきまが大きいので、液体から個体になるときに密度が低下する。
このため、氷(こおり)の密度は水(みず)よりも大きいので、氷は水に浮く。
このように、液体よりも固体のほうが密度が小さいのは、H2O分子に特異的な現象である。H2O分子をのぞく他の多くの物質では、液体よりも固体のほうが密度が大きいのが普通である。
金属
[編集]- 金属結合:

例として鉄で説明するとしよう。合金ではない鉄の結晶で説明する。鉄の結晶は、結晶全体で電子を共有している。だからこそ、外部から鉄に電流を流そうとすると、鉄には電気を流せる。鉄に限らず銅の結晶やアルミニウムの結晶でも、同様に、結晶全体で電子を共有している。
このように結晶が鉄や銅やアルミニウム等のような結晶を金属結晶)と言い、分子の単体がそのような性質をもつ元素を金属元素と言う。その金属元素の単体(ここでの「単体」とは、合金ではないという意味)の結合を、金属結合(metallic bondという。
また、このような結晶全体で共有された電子は結晶中を、ほぼ自由に移動できるので、金属中の電子のことを自由電子(free electron)という。つまり、金属内の電子は、その結晶全体を動け、けっして特定の原子には拘束されない。
電子殻の視点で見れば、金属結晶では個々の電子殻は、実際に電子殻を周辺の多くの原子と共有している事になる。金属結合は、けっして共有結合とは違う。金属結合は、けっして共有結合のように特定の原子間で電子を共有しているのでは無い。
また、金属は導電性が高い。また、熱も伝えやすい。この導電性や熱の伝えやすさも、自由電子の性質が理由である。根拠は下記のとおり。
Ag,Cu,Au,Al,・・・などの金属原子ごとに、熱伝導率と電気伝導率を比べると、電気伝導率が高い原子ほど熱伝導率も高い原子であるという相関関係をもつという実験的な事実がある。この事から、金属の熱伝導の高さの理由は、自由電子によるものである。
なお、金属を熱すると導電性は下がりる。(つまり、金属を熱すると、電気抵抗は上がる。)
(※ 補足: 範囲外 )また、金属原子は、(共有結合する原子などと比べると、自由電子という性質のため)電子の広がらせやすさが大きい。
(※ 範囲外: )なお、一般に黒鉛は金属には分類しない。黒鉛は電気を通すが、しかし、この節で述べるような性質をあまりよく満たさない。黒鉛などを「半金属」という場合もある(※ 「半導体」とは異なる)。
展性と延性
[編集]
金属を強く叩く加工をすると、箔状に広げることが可能だが、箔状に広げても、金属がつながったままで、割れたり切れたりしにくく、叩いても金属がつながったままで広げやすい性質を展性(てんせい,ductility)という。また、金属を伸ばして線状に引き伸ばしても、切れにくくつながったままの性質を延性(えんせい,malleability)という。 この展性や延性は、自由電子による。金属結合が自由電子による結合なので、加工によって変形をしても、原子の配列が変わっただけで、金属全体では自由電子を共有しつづけるので、金属結合を維持し続けるからである。
金属光沢
[編集]金属には光沢が有る。これは、金属表面で光の反射が起こるからである。より正確に言うと、光をいったん吸収して、その直後に再放出をするので、反射をする。金属によっては、全ての波長を反射せずに波長の一部の光を吸収するので、その結果、金属は色みを帯びて見えることになる。
銀では、ほぼすべての入射光を反射するので、銀白色に見える。(白色とは、可視光の波長が全て揃っている光の状態である。) 銅や金など、色づいて見える金属は、入射光の一部の波長の光を金属が吸収している事による。
金属結晶
[編集]金属結合では、原子は規則的に配列をして結晶を作る。金属の結晶の配列を結晶格子(けっしょうこうし, crystal lattice)といい、その結晶格子の最小となる単位を単位格子(たんいこうし, unit cell)という。 その結晶の種類には3種類が有ることが知られている。列記すると、
- 面心立方格子 (めんしん りっぽうこうし, face-centered cubic) (例):Al, Cu, Ag, Ni,Au, Pt など
- 体心立方格子 (たいしん りっぽうこうし,body-Centered Cubic ) (例):Fe, W, Ba、およびアルカリ金属のLi, Na,K, など。
- 六方最密構造 (ろっぽう さいみつこうぞう,hexagonal close-packed ) (例):Zn, Mg, Co など
である。
-
面心立方格子の模式図
-
体心立方構造の模式図
-
六方最密充填構造
配位数
[編集]結晶の配列を見た時に、ひとつの原子に最近接している原子が何個かを表した数を配位数(はいいすう, coordination number) という。結晶格子の種類によって配位数は決まる。配位数の計算では、単位格子の図では省略された隣の格子の近接原子の数も考慮しなければならない。
- 面心立方格子の配位数
たとえば、面心立方格子では配位数は12である。 配位数の算出の数え方では、まず単位格子を見る。単位格子の図だけだと面心立法格子では、面の中心の原子には8個が近接しているが、この図はあくまでも単位格子だけの原子を表したものにすぎない。実際の結晶配列では、単位格子のとなりには同じ配列の格子が繰り返しているので、そのような単位格子の図では省略された近接原子の数も考慮しなければならない。図示で省略された分の近接原子数も数えると、省略された最近接原子は、4個である。
したがって、これらを足しあわせた数が配位数である。つまり、単位格子図上のある1個の原子に注目した場合に、
- (単位格子の図だけで見た最近接原子の数) + (単位格子の図では省略された、隣の格子にある最近接原子の数)
を計算する。面心立方格子では、配位数を計算すると、
(単位格子の図だけで見た最近接原子の数)=8
(単位格子の図では省略された、隣の格子にある最近接原子の数)=4
なので、最終的に配位数の合計は
- 8 + 4 = 12
となるので、面心立方格子の配位数は12である。
- 体心立方格子の配位数
つぎに体心立方格子の場合に配位数を考えよう。 「体心」という名の通り、単位格子の立体の中心にある原子に注目して配位数を計算すると、計算がラクである。 まず、他に格子の図上だけで見た、格子中央の原子の最近接原子数は8である。
- (単位格子の図だけで見た最近接原子の数)=8
つぎに、単位格子の図で省略された隣の格子の原子は、この単位格子の中央原子とは接触していない。つまり、「最近接」はしていない。なので、
- (単位格子の図では省略された、隣の格子にある最近接原子の数)=0
である。
これより配位数は、
- (単位格子の図だけで見た最近接原子の数) + (単位格子の図では省略された、隣の格子にある最近接原子の数) = 8 + 0 = 8
となり、体心立方格子の配位数は8である。
- 六方最密構造の配位数
6角形の真ん中の原子に注目すると計算がラクである。 まず、単位格子図上では9個と接触している。(6角形の6個と、下の3個)。6角計の上の3個を足して、合計12個である。 よって六方最密構造の配位数は12である。
単位格子中の原子数密度
[編集]単位格子中の原子数密度を求めるには、まず、その単位格子1個につき幾つの原子が所属しているかを計算する必要がある。なお、間違えて配位数を計算しないこと。
- 体心立方格子の原子数

立方体の隅の原子の、格子に属する部分の大きさは原子1個につき、球のである。この大きさが 球の
の原子が、8箇所ある。格子中央の原子は球の大きさすべてが格子に含まれている。よって格子中央の原子の大きさは球の
合計すると、
よって、体心立方格子の所属原子数は、2個である。
- 面心立方格子の原子数
- (※編集者へ. 図を作図のこと)
面心立方格子では、立法体の隅の原子は、格子に属する部分の大きさが球のである。この大きさが の原子が、8箇所ある。 よって、まず、
となり1個以上の原子が属することが分かった。続けて、他の原子も数える。 面の中央の原子は、大きさが、球の である。面は6面あるので、大きさ の原子が6箇所ある。
合計すると、
よって、単位格子中の所属原子数は4個である。
- 六方最密構造の原子数
- (※編集者へ. 図を作図のこと)
六方最密構造の所属原子数は、図から分かるように。2個である。
原子半径と充填率
[編集]原子半径
[編集]
密度を求めるには、単位格子の1辺あたりの長さを知らなければならない。もし、原子半径 r と、単位格子の1辺あたりの長さ l には、図からわかるように、次の関係がある。
体心立方格子の場合、原子半径rと、単位格子の1辺あたりの長さ l との関係式は、図のように三平方の定理より、
よって
である。

面心立方格子の、原子半径rと、単位格子の1辺あたりの長さ l との関係式は、三平方の定理より、
である。
充填率
[編集]単位格子中に原子の占める体積の割合を 充填率(じゅうてんりつ) という。充填率を計算で求めるには、定義どおりに、単位格子中の体積を、単位格子の体積で割れば、求まる。
- 体心立方格子の場合
まず、単位格子中の原子の体積は、以前の節で説明したように、原子2個ぶんの体積である。
つまり体積は、
である。
そして、 体心立方格子の場合の原子半径rと、単位格子の1辺あたりの長さ l との関係式は、前の節で計算したとおり、
なので、代入するなどして連立方程式を解けば、充填率が求まる。
- 充填率 =
よって体心立方格子の充填率は 68% である。
- 面心立方格子の場合
- 充填率 =
よって面心立方格子の充填率は 73% である。