高等学校工業 原動機/流体の性質と力学
これから、流体について様々な知識を紹介する。
だが、工場などで流体機器を扱うさいの実務の基本は、まずは正しい組み立て法で装置を組み立て、正しい使用法で使用することである。
また、高校では毒性の高い物質を流体として扱う機会は無いだろうが、実務で毒劇物などの漏れがあると事故につながる。
大学レベルの「流体力学」(りゅうたい りきがく)の専門書などを読むと、微分方程式などの数式が多く出てきたりするので、てっきり数式だけで流量測定の実務が片付きそうに誤解しそうになるかもしれない。だが、流量計を扱う企業での実務内容は、たとえば流体機器の溶接や組み立てなどを確実に行うことである。
たとえ流体力学に出てくる微分方程式(びぶん ほうていしき)などの計算が出来ても、継ぎ手を締める工具や溶接機具などの取り扱いが出来なければ、その工具が出来ない人は製造業の工場では使い物にならない。
流体現象の計算式を研究し解明するのは物理学者や工学者などの科学者の仕事であり、工場労働者の仕事では無い。 工場で使う流体についての数式なんて、せいぜい工業高校で習うようなレベルの式である。 そもそも工場で微分方程式を解く機会は少ない、はっきりいうと中小企業では微分方程式を要求される機会は「無い」だろう。
だから、たとえ流体力学の微分方程式を解けても、工場では需要が無い。そういう工具などが出来ない人は、たとえ微分方程式の計算が出来ても、製造業とは別の職業を目指したほうが良いだろう。
流体の密度
[編集]液体(liquid)および気体(gas)をあわせて、流体(りゅうたい、fluid)という。流していなくても流体と呼ぶ。流体の運動方程式を考える場合は質量(mass)の代わりに密度(density)を用いることが多い。密度の記号はρ[kg/m3]が多い。
密度の定義式は
(密度の単位は[kg/m3])
- m:物体の質量。[kg]
- V:その物体の体積。[m3]
密度は、定数とは限らないことに注意する必要がある。例えば、ビニール袋や風船に気体をつめた場合を考えれて見よう。圧力を加えれば圧縮し、熱を加えて温度を上げれば膨張する。 このように密度が変化する流体を圧縮性流体といい、そのような性質を圧縮性(あっしゅくせい)という。 空気や、酸素ガス、炭素ガス、窒素ガスなどは、気体の範囲ならば圧縮性流体として扱って良い。 蒸気は圧縮性流体とみなして良い。
いっぽう、水などの液体の場合は、密度は定数と見なしてよい。このような密度を定数と見なせる流体を非圧縮性流体といい、そのような性質を非圧縮性(ひあっしゅくせい)という。
粘性
[編集]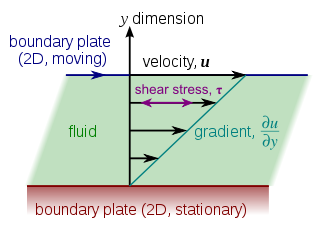
流体の流れている速度を流速(りゅうそく)という。 流れている流体は、流体内部の流速に、隣の流れと速度差がある時に、その差を無くそうとする抵抗力が働く。流速の大きい側は抵抗力によって流速が下がり、また、流速の小さい側は流速の大きい側に引きずられて流速が大きくなる。この流速の差に比例する抵抗力、隣の流れを引きずろうとする性質をを粘性(ねんせい、viscosity)という。粘性を定量化したものを粘度(ねんど)や粘性係数(ねんせいけいすう)といい、記号は一般にμで表す。単位は[Pa・s]である。
この単元では、とくに断らないかぎり、液体の粘度について、考察する。
- (※ 範囲外: )実務的には、粘性によって、その流体の速度が低下する。(あまり機械工学の教科書では、粘性による速度低下の性質については書かれてないのだが、しかし生物学や化学などの大学教科書には書かれている。) (※ 参考文献: LODISHなど著『分子細胞生物学 第7版』、翻訳出版:東京化学同人、翻訳:石浦章一など。 原著はアメリカのマサチューセッツ工科大学やカリフォルニア大学の生物学者などが著作している。 )
- (※ 範囲外: )粘度の測定方法については、いくつかの方式がある。生物学や化学などでは、「オストワルド粘度計」というのが、よく使われている。これは。U字管の内部に毛細管があり、その毛細管の上にまず液体をため、その真下に毛細管があり、落下時間を測定することにより、粘度を測定するという方式である。比較的に粘度のひくめの液体の粘度を測定する場合の、よくある実務的な測定方法である。
- このほか、「回転粘度計」というのもあり、円筒容器に流体をいれ、中央軸で かくはん羽根 を回して、トルクが外側の円筒にどの程度、伝達するかを測定することで粘度を測定する原理のものもある。)
- 粘度計についての市販の書籍はすくない。もし粘度計についての書籍が必要なら、流体力学ではなく「流体計測」「流体測定」などの専門書を読むか、あるいは一部の『物理化学』の大学教科書に書いてある。大学の理工学部の学科で『化学科』というのがあり、その学科の専門科目で『物理化学』という科目があり、その『物理化学』科目の教科書で、粘度計の図や解説があったりする。
さて、機械工学や物理学では、粘性の式については、下記のようになる。粘性の式については、抵抗力をF、速度の差をΔv、位置の差を Δy、二つの流れが接してる面積をAとした場合、式は
である。この力の方向は二つの流れの接触面に平行の方向である。だから、この力は、せん断力である。
したがって、単位体積あたりで考えれば、接触面にせん断応力τがかかり、その大きさは、
である。
粘性が、このような式で表される流体をニュートン流体(Newtonian fluid)という。この「ニュートン」とは、この法則を研究した物理学者のアイザック・ニュートンのことである。べつに力の単位のニュートンのことでは無いので混同しないように。水の液体の粘性を扱う場合は、ニュートン流体として扱って良い。
粘性による抵抗が、ニュートンの法則に従わない種類の流体を非ニュートン流体というが、高校レベルでは一般に扱わない。ある種の高分子液体などでは、外部からの力のかけ方や流速によって粘度が変わる流体などが知られている。
粘性は、隣の流れへの運動量の拡散しやすさである。
- その他(※ 範囲外)
たとえば、デンプンが溶けた水では、水量に対してデンプンの量が多いほど、粘度が高いだろう。このように、一般に高分子の物質の溶けた流体では、溶質の量が増えれば増えるほど、粘度も大きくという傾向がある。
いっぽう、分子量の低い分子(たとえば食塩)などを溶かしても、あまり粘度が上がらない。
このような化学的な性質を活用して、溶液に溶けた溶質の分子量を測定したい場合に、粘度測定により分子量を測定する「粘度平均分子量」という方法がある。この粘度平均分子量という方法は、溶質が高分子の場合に有効である。
圧力
[編集]水中の物体の表面にかかる水圧などのように、流体では一点集中の集中荷重ではなく、分布して力がかかることが多い。そのため、単位体積あたりの力に換算する必要がある。このある面に垂直にかかる単位体積あたりの力を圧力(あつりょく、pressure)という。圧力の定義対称は液体だけでなく、気体にも圧力は定義される。
圧力の単位は[N/m2]であるが、これをパスカル[Pa]という単位であらわすことが一般である。
- [N/m2]=[Pa]
である。
水圧について
[編集]容器のなかに液体が入って静止している場合について、液体内の、ある水平面(ここで言う「水平面」とは、重力方向に垂直な面のことで、水の表面のことではない。)にかかる力は、その真上にある液体の重さによる力である。
ある面の面積をA[m2]、その深さをh[m]、ρを液体の密度[kg/m3]、gを重力加速度とすると、 ρhA[kg]が液体の質量になる。したがって、重さによる力は、これに重力加速度をかけたρghA[N]になる。 圧力は単位体積あたりの力だから、つまり、
- [Pa]
ゲージ圧と絶対圧
[編集]圧力の数値の基準点は、2種類ある。いっぽうは、大気圧を圧力のゼロとして、測った圧力であり、ゲージ圧(ゲージあつ、gauge pressure)という。もういっぽうは、まったく気圧のない状態を圧力のゼロとして測った場合の圧力を絶対圧(ぜったいあつ、absolute pressure)という。つまり、
- ゲージ圧 + 大気圧 = 絶対圧
である。 圧力が大気圧以下のことを真空(しんくう、vacuum)という。そして、完全に気圧がない状態を、絶対真空(ぜったいしんくう、absolute vacuum)という。
気象学などでは、絶対圧を用いることが多い。 通常の圧力計は、ゲージ圧を測る圧力計である「ゲージ圧計」の場合が多い。 圧力が大気圧以下の場合は、数学のマイナス符号を用いてゲージ圧を表す。この大気圧以下のゲージ圧を負圧(ふあつ)という。いっぽう、大気圧より上の圧力を正圧(せいあつ)という。負圧を測る場合は、真空計などの専用の圧力計で測る。 ゲージ圧の場合の「大気圧」とは、測定地点の気圧のことであるので、室内環境や気象などによって変わる。
パスカルの原理
[編集]
密閉した容器の液体の一部に圧力を加えると、その圧力は、液体のすべてに伝わり、同じ大きさの圧力のまま伝わる。この法則をパスカルの原理(パスカルのげんり、Pascal's principal )という。この原理を応用した装置としては、油圧装置などによる力の増幅などの例がある。
たとえば、図のようなピストンがあって、ピストン1の面積をA1[m^2]、ピストン2の面積をA2[m^2]、ピストン1の力をF1[N]、ピストン2の力をF2[N]とする。 ピストン1を押したとき、発生する圧力は、
- [Pa]
この圧力Pがピストン2にそのまま伝わるので、
- [Pa]
である。 つまり、
- [Pa]
F_2は、
- [N]
である。 つまり、ピストンの面積比 に応じて、力は拡大される。これが油圧ジャッキなどにおける力の拡大の原理である。
次に、ピストンの移動する距離を求めよう。 液体は非圧縮性なので、ピストン1から押し出された液体は、その分、ピストン2に流れ込む。したがって、次の関係式が成り立つ。
- [m3]
これをピストンがおこなった仕事のエネルギー量に関して考えてみる。力学における仕事の定義は、「力×移動距離」である。ピストン1の仕事をW_1 [J]とし、ピストン2の仕事をW_2 [J]としよう。
- [J]
- [J]
さて、
- [N]
の面積比に、体積の関係式の
- [m3]
の関係を代入しよう。まず、代入しやすいように、変形すれば、
である。
これより、
- [J]
となり、仕事は保存する。
流れの力学
[編集]定常流と非定常流
[編集]流れの速度や方向などの状態が、時間の経過によっては変わらない場合の流れを定常流(ていじょうりゅう、steady flow)という。時間の経過によって流れ方が変わる場合を非定常流( ひていじょうりゅう、unsteady flow )という。
流速
[編集]流体の流れる速度を流速(りゅうそく、flow velosity)という。流速vの単位には[m/s]を用いる。(一般の速度の単位と同じ。)
流速は、管路内では均一とは限らない。管壁の近くでは、管壁との摩擦のため速度が下がる。計算の簡単化のため、流速を平均化したものを平均流速という。単に「流速」といった場合、この平均流速を指す場合もある。
流量
[編集]管路内を流れる流体について、考えよう。 体積流量 流速が大きくても、管路の幅が小さければ、流れる液体の量は小さくなる。とすると、流れの量を定義するには、流速vに断面積Aをかけた積の、Avで定義すればよさそうである。 これが、体積流量(volume flow rate)の定義である。 つまり、体積流量Q[m^3/s]の定義は、管路の断面積をA[m2]、流速をv[m/s]とすれば、
である。
気体の流れの場合、高温での気体の流れの場合は、体積が一定でも、温度によって気体の密度が変わるので、体積流量では不都合な場合がある。 このような場合をかんがえれば、密度ρ[kg/m3]を、体積流量にかけた流量を、新たに定義すれば良さそうである。 流体について、単位時間に断面を通過する質量を質量流量(mass flow rate)という。 式は、密度をρ[kg/m3]、管路の断面積をA[m2]、流速をv[m/s]とすれば、質量流量q_mの式は
である。 高温での気体流体の計算では、質量流量が用いられる場合が多い。また、化学工業での流体計算でも、体積流量よりも質量流量のほうが化学反応量の計算がしやすいという都合から、質量流量が用いられることもある。
体積流量を単に流量と呼ぶことが多く、特別な理由がない限り、工業では、こちらが使われることが多い。
連続の式
[編集]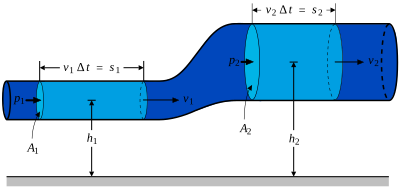
管路の幅が変化する場合、定常流だとして、管路が1本だとして、漏れなどによる外部流出が無いとすれば、質量流量は、 A_1から流れだした量は、下流のA_2へと流れこむし、そのぶんだけ、流れこむ前に元からA_2にあった流体は、より下流に流れ出すことになる。よって、以下の式が成り立つ。
- [kg/s]
これを、流体における連続の式(continyuity equation)とか、連続の法則という。
水などの非圧縮性流体では、密度が定数とみなせるので、
- [m3/s]
である。
流体のエネルギー
[編集]圧力とエネルギーの関係
[編集]まず、高さが変わらない水平な管路を考える。説明の簡単化のため、円形断面の管路の中を流れるとする。 流体が下流へと流れるには、まず上流のほうが下流よりも圧が高いという圧力差が必要である。 いっぽう、エネルギーの定義は、それを物体に与えることによって、与えられた物体を動かす事ができる能力である。これらの事を合わせて考えて、圧力をエネルギーの種類のひとつとして解釈する考えもある。実際、次元を見れば、圧力の次元[Pa]=[N/m^2]は、単位体積あたりのエネルギーの次元[J/m3]=[N/m3]と等しい。
なお、ある流れでの2点間の圧力差を、差圧(さあつ、differential pressure)という。 液体が満ちている管路の上流と下流に差圧があれば、上流側が圧が大きいとすれば、流れは下流へと流れる。
流体の運動エネルギー
[編集]まず、液体の場合について、流体の運動エネルギーを考える。説明の簡単化のため、円形断面の管路の中を流れるとする。また、流れは均一だとして、渦などの流れを均一でなくす現象は発生してないとする。 流体であっても、質点の力学の運動エネルギーと同様に定義できる。流体であろうが、質量のある物体には変わりがない。仮定より、流れは均一であるとした。 すると、ある仮想区間内での流体の合計質量をm[kg]として、流速をv[m/s]とすれば
- [J]
で運動エネルギーを考えられる。 単位体積あたりに直せば、
- [J/m3]
が、流体の単位体積あたりの運動エネルギーである。
流体の位置エネルギー
[編集]液体が上から下へと流れる現象を考えれば分かるように、管路の上流と下流に高低差があったとして、上流のほうが位置が高ければ、とくに上流に圧力を加えなくても、流体は流れる。 つまり、流体は位置エネルギーを持っている。流体であっても、物質であることに変わりはないから、位置エネルギーを、とうぜんに持っている。 単位体積あたりの流体の位置エネルギーは
- [J/m3]
である。
流体のエネルギー
[編集]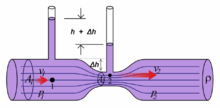


流体のエネルギーは以下の式で表される。
- [Pa]
この関係式をベルヌーイの定理(Bernoulli's principle)という。 速度vがゼロの場合を考えてみれば、ベルヌーイの式は、水圧の深さと水圧の大きさの関係式の拡張になっている。 位置が変わらない流れの場合、式によると流速が上がると圧力が下がる。実際に、断面積を細めるなどして流速を高めると、このような圧力低下の現象は起こり、この現象をベンチュリ効果(Venturi effect)という。この効果を利用した装置として霧吹きなどが知られている。
ヘッド
[編集]ベルヌーイの定理の式は、以下のように、長さを次元とした式に変形できる。
- [m]
を速度ヘッド(velosity head)という。 を 圧力ヘッド(pressure head)という。第三項を位置ヘッド(potential head)という。これら全てを足しあわせた値を全ヘッド(total head)という。
トリチェリの定理
[編集]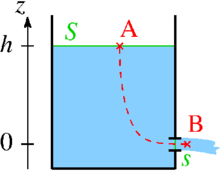
水槽の下方に穴が空いてたとしよう。大気中に流出する流量を考えよう。また、説明の簡単化のため、水槽の容量はじゅうぶん大きく広く、水が流出しても、水深hの変化はゼロと近似できるとする。 他の仮定として、摩擦などの損失や、流出の際の空気抵抗は考えないとする。 つまり、
- .
とする。
また水面が広いため、上流側の水面の流速v_1はゼロに近似できるとする。
ベルヌーイの定理を用いて、流出速度v_2を求めよう。
- .
まず、圧力p_1、P_2は共に大気圧に等しく、差圧はゼロである。
また、浴槽の水深は仮定より一定であり、これから水面と流出口の位置エネルギー差は一定である。 つまり
また、仮定より、上流の流速はゼロである。
流体は非圧縮性の液体であり、密度ρは一定である。 これ等の式をベルヌーイの定理の式に代入すると、いくつかの項がゼロとなって消え、残る項の関係式は
となる。求めたいのはv_2であったから、移項してこれを求めれば良い。h=(z_1-z_2)を利用して、結果は、
である。
層流と乱流
[編集]


レイノルズは図のような装置を用いた実験を行った。通常の透明な水の流れに、着色液を流す実験を用いて、流体中での流れを可視化した実験を行った。その実験の結果、流れがある速度を超えると、着色液の線は乱れ不規則になり、周囲の透明水と混合していく現象を発見した。 流れの線が真っすぐな状態を、層流(そうりゅう)と言い、不規則で混合していく状態を乱流(らんりゅう)という。
より詳しく言うと、流体におけるある区間において、流速が低速の場合は、流れの方向がそろっていて、一様に下流に流れる。管壁の近くは摩擦のため、多少は速度差が生じる場合があるが、それでも下流に流れていることには変わらない。ともかく、これらのような、流れの方向が一様な流れを層流(英:laminar flow)という。だが、流れの速度が高い時などは、長期的には下流に流れるものの瞬間的・短時間的には不規則な流れがおこることが確認される。このような不規則な流れを乱流(英:turbulent flow)という。 流れが層流から乱流に変化することを遷移(せんい)という。
レイノルズ数
[編集]レイノルズは、より詳しい実験を行った。水の平均流速vおよび、管の管径dを変えて、同様の層流と乱流の遷移をしらべる実験を行った。また、温度を変えることで粘性μを変えても、遷移の実験を行った。
その結果、次の法則を発見した。無次元数(ρvd/μ)がある値になると、層流から乱流に移る。 彼の、この功績から、この無次元数は、後にレイノルズ数(Reynold's number)と呼ばれるようになった。 レイノルズ数の数式記号はReで表す。つまり、レイノルズ数の定義式は、
である。 実験の仕方にもよるが、水の流れにおいて、レイノルズ数Reを変えていって実験をすると、レイノルズ数Reがおよそ2300のあたりで、流れが乱流になることが多い。(文献によっては2000のあたりで乱流になると報告するものもあるが、ともかく、それらの値の周辺であることが多い。)流れが層流から乱流に変わるときのレイノルズ数Recを臨界レイノルズ数(critical Reynold's number )という。この値は実験によって実測値から決める。通常の実験では、臨界レイノルズ数の値は、およそ2300の周辺であることが多い。
レイノルズ数の式について、調べていこう。まず、次の概念を準備する。
慣性力と粘性力
[編集]川の流れなどが物を運べるように、流れている流体は、力を及ぼすことができる。その力はρv^2に比例する。ρv^2を慣性力という。この式を見ると、運動量ρvに速度vをかけたものになっている。流体も運動量を持つ。流体であろうが物質に変わりないから運動量を持つ。力学で言う力の定義とは、運動量の単位時間あたりの増加率でもある。
ある区間の断面に上流から運動量p(=ρv)が速度vで流れこむ場合、
で、ある区間に、上流から運動量が流れ込む。 このように、流体に関して、運動量をもった流体が流れてのいる時に、運動量pにその速度vをかけた積vpを運動量密度という。
定常流で、流速が一定なのは、上流から流れこんできた運動量密度と同量の運動量密度が下流から流れ出て、上流と下流で差し引き運動量の増減はゼロになるからである。
さて、流体は、それによって物を動かせるのだから、力を持っている。その力は、およそρv^2に比例する。このρv^2を慣性力というのであった。
また、粘性の定義が速度勾配に比例する抵抗力であった。管路の幅をLとし、流速をvとする。このとき、次の式、
を粘性力という。
実は、レイノルズ数(Reynold's number)は、粘性力と慣性力ρv^2の比である。
なお、粘性係数μを密度ρで割った値μ/ρを動粘度と言いνで表す。
これを用いた場合、レイノルズ数は次の式で表される。
流体実験では、管の大きさなどが違っても、レイノルズ数が同じなら、観測される流体現象は同じであることが多い。説明では、管路を流れる水の流れで説明したが、空気など気体の流れでも同様にレイノルズ数を定義できる。また、静止した流体中を、機械が運動するとき(たとえば大気中を飛ぶ飛行機など)にもレイノルズ数は定義できる。(飛行機の場合はここでは説明しない。)機械が制し流体中を移動する場合、長さLには機械の幅などの長さを、代表長さとして取る。
流れのエネルギー損失
[編集]摩擦損失
[編集]直管において、管路を流れる流体の摩擦によるエネルギー損失の式は、比運動エネルギーv^2/2と、管路の長さLに比例し、内径dに反比例する。無次元の係数λをもちいて、次の式で表される。
この式を、ダルシー・ワイスバッハの式(Darcy–Weisbach equation)という。ダルシー・ワイスバッハの式での係数λを管摩擦係数(friction factor of pipe)という。λの値は流れの状態によって変化する。λの値を与える式は、層流の場合は理論的な式が知られている。導出は、高校レベルを超えるので導出はしない。導出の概要を述べると、「ハーゲン・ポアズイユの式」(Hagen-Poiseuille equation)という式の解析から得られる。結果を述べると、
である。
乱流の場合のλの式は、様々な式が提唱されている。 だが、実務上は業界慣習に従って決めたり、実験結果をもとにして得られたムーディ線図(Moody diagram)と呼ばれる図表から決定する場合が多い。
たとえば、実用上、鋼管の場合は、管壁の粗さに関係なくλ=0.03を用いることもある。 実務については教科書レベルを超えるので、これ以上は説明しない。
ムーディ線図を用いる場合は、レイノルズ数Reと、管壁の相対粗さε/dを用いる。dは管内径である。εは粗さの絶対値である。また、横軸のレイノルズ数は対数目盛であることに注意。レイノルズ数が大きい場合は、ほとんどε/dの影響によって、管摩擦係数が決まり、レイノルズ数の影響は相対的に小さくなる。

管路形状による損失
[編集]管路に曲がりがあったり、断面積が急激に変化したりした場合の摩擦損失を考えてみる。直管の場合の摩擦損失と比べれば、当然に、管路に曲がりや急変があるばあいのほうが損失は大きい。 管路の形状に応じた損失係数が定義されている。損失係数の記号はζ(ジータ)である。次の式で定義される。
損失を生じる場所の前後で速度が変化する場合は、大きいほうの流速を、式のvの値に取る。












































