高等学校工業 原動機/熱力学の基礎
式中の圧力は、特に断らない限り、絶対圧である。
状態方程式
[編集]式中の温度は特に断らない限り絶対温度(単位はケルビン[K])である。
物理学や化学などでの熱力学で知られるボイル・シャルルの法則では、理想気体の状態方程式は次の形である。
が成り立つ。式中のPは絶対圧での圧力[Pa]。Vは気体の占める体積[m3]。Tは気体の絶対温度[K]である。 このとき、定数 はガス種によらず一定である。
- [J/(mol・K)]
である。この定数 を普遍気体定数(universal gas constant)または一般気体定数と呼ぶ。
機械工学および流体力学では、モルnの代わりに、質量mを使い、次の式に変形された状態方程式を使うことが多い。
比例定数R[J/(kg・K)]はガス種によって変わる定数なので注意。この係数Rを気体定数(gas constant)という。分子量をMとした場合、
- [J/(mol・K)] ( =8.314[kJ/(mol・K)] )
の関係がある。 気体定数は便覧などに与えられているので、それを用いることが多い。機械工学では、あまり、モルから熱力学の諸量を算出することはしない。機械工学で質量mを用いた状態方程式を用いるのに、とくに明確な理由があるわけではないが、用いる理由を強いて言うなら、流体力学との関係上、運動方程式を扱いやすいことや、測定の都合で、モルを測定するより質量mを測定するほうが容易な場合が多いなどの理由だろう。
なお、体積のVを右辺に移行すると、密度ρが、式に出てくる。
ここで、小文字のvを用いて、密度の逆数を比体積と定義する。 つまり、比体積vの定義は
である。
エンタルピー
[編集]気体の内部エネルギーUに圧力Pと体積Vの積PVを足しあわせた量U+PVをエンタルピー(enthaipy)という。 エンタルピーを記号Hで表す。
- [J]
が定義である。 圧力一定の定圧変化の比熱c_Pは、エンタルピ変化に等しくなる。 なぜなら、
いっぽう、
で仮定の定圧変化より\Delta P=0だから、
流体に熱が加わる場合の流体計算では、エンタルピを用いたほうが、式の形が単純になることが多い。
温度変化が無い等温変化(isothermal change)では、圧力や体積がどう変わってもエンタルピは変化しない。 なぜなら、U+PVとPV=mRTを連立させると、
となるが、内部エネルギUは理想気体では、温度のみの関数だから、
となる。
エントロピー
[編集]熱機関の効率は以下の式で定義される。温度の高温部から熱量が機関に入り、温度の低温部に熱量を出した場合、効率の定義式は
である。熱機関の最大効率は、可逆機関の場合であり、その式は、温度を用いて、
と表せる。 現実の熱機関は、不可逆機関であり、効率は理論上の最大効率よりも下がる。 さて、不等号を用いて、可逆機関と不可逆機関の両方の場合をまとめて表せば、
- ≦
である。これを変形し、
- ≦
- ≦
- ≦
と表せる。
ここで、熱量Qを温度Tで割った値Q/Tが出てきたが、この量をエントロピー(entropy)といい、記号Sを用いて次の式で定義される。
- [J/K]
エントロピを用いると、熱効率の式は次の形に書き換えられる。
- ≦
となり、不可逆過程の場合は、熱機関の中でエントロピが増加して、放出されたことになる。 なお、エントロピーは、名前がエンタルピーと似ているが、異なる量なので混同しないように注意すること。
機械工学では、蒸気の熱計算でエンタルピーやエントロピーを使うことがある。
蒸気の性質
[編集]用語
[編集]本章では、「蒸気」と言った場合、特に断らない限り、水蒸気とする。化学など、ただし、他の学問分野では、水蒸気以外のものも、たとえばアルコール蒸気なども、蒸気に分類するので、化学の教科書などを参照するときは注意が必要である。 また、室温や常温での水の蒸発などのように、蒸気は、沸点から低くても発生する。だが、本章では、沸点への加熱によって蒸気を発生させた場合を中心に、特に断りがない限りは、扱うとする。
液体の沸騰する温度は、その液体に加わる外部からの圧力によって変わる。 誤解をされやすいが、実は蒸気は沸点以上にも加熱することができる。 「蒸気は沸点以上に加熱できない。」という考えは、大気圧状況に解放された容器内の沸騰水にのみ対してしかなりたたない。 沸点以上の加熱の例は、たとえば、金属製の強固な密閉容器中に、水と空気を閉じ込めて、沸騰させれば、容器密閉のため圧力は大気圧一定ではないので、加熱を続ければ沸騰開始時の温度よりも蒸気の温度は上がる。本章で解説しようとしてるのは、このような、大気圧での沸点以上に加熱された蒸気の性質である。
このように大気圧以外の圧力状況でも、水の沸騰を扱うことから、本分野では水の沸点は、必ずしも大気圧状況での沸点100℃とは限らない。
このような理由から、以下の飽和圧力、飽和温度の定義が必要である。
- 飽和圧力
ある一定の温度の条件化で液体が沸騰するときの圧力を飽和圧力(saturation pressure)という。また、ある一定の圧力下で、液体が沸騰するときの沸点の温度を飽和温度(saturation temperature)と言う。 液体の飽和温度は、圧力が下がれば飽和温度も低下するのが一般である。
飽和温度と飽和圧力の状況のもとにある水を、飽和水(saturated water)という。
沸騰している液体から発生する蒸気は、飽和温度と飽和圧力の状態にあると考えられるので、この蒸気を飽和蒸気(saturated steam)という。
沸騰の間、液体が全て気体に変わって無くなるまでの液体が残っている間は、大気中に蒸気を開放するなどして圧力を沸騰開始時のままに一定に保てば、蒸気の温度は飽和温度から変化しない。
- 湿り飽和蒸気
飽和蒸気と飽和水との混合物を湿り飽和蒸気という。これに対して、湿り飽和蒸気を加熱させるなどして飽和水を全て飽和蒸気に変えて、水分をまったく含まなくなった直後の飽和蒸気を、乾き飽和蒸気という。
湿り飽和蒸気の質量1kgあたりに対して、x[kg]が飽和蒸気であるとき、x[kg]の値を乾き度(dryness)と言い、(1-x)の値を湿り度(wetness fraction)という。日本語での「湿り度」の表記が、地学用語などの「湿度」(humidity)と似ているが、定義は別物であるので混同しないように注意のこと。 乾き度xを用いて乾き飽和蒸気の定義を説明すれば、乾き度x=1に成った直後と同じ状態の温度・圧力の蒸気を乾き飽和蒸気という。乾き度x=0の状態は、飽和水である。
各種の線図
[編集]
"Liquide-vapour"が気液共存の領域で、湿り蒸気。
"Courbe de rosée"とある、緑領域と水色領域との、境界線の黒線が、飽和蒸気線である。 "Courbe d'ebulition"は飽和水線のこと。
蒸気の性質は、温度や圧力の各条件の値によって、様々な場合があり、ひとつの式では条件と蒸気の状態を表現しにくいことから、グラフによって、条件と蒸気状態との対応を表現する場合がある。そのためのグラフとして以下に述べるような各種の線図がある。 代表的な線図として、蒸気の温度と体積の関係をグラフ表示したT-v線図がある。 他にも、蒸気の圧力と体積の関係をグラフ表示したP-v線図がある。 さらに他にも、蒸気の圧力と温度の関係をグラフ表示したP-T線図がある。
線図上で飽和水の条件をプロットした点を、つなげた曲線を飽和水線(saturation water line)または飽和液線(saturation liquid line)という。 線図上で飽和蒸気の条件をプロットした点を、つなげた曲線を飽和蒸気線(saturation vapour line,あるいはsaturation steam line)という。
臨界点
[編集]
水蒸気の線図では、常温・常圧から高温へとなるに従い、飽和液線と飽和蒸気線の両線は近づく。そして、次の点の、圧力22.064MPa、温度373.946℃の点で、飽和水線と飽和蒸気線とが交わる。この点を臨界点(critical point)という。
(なお、「臨界点」という言葉は、他の分野でも違う意味で用いられることが多いので、混同しないように注意のこと。)このときの比体積は、0.00310559m^3/kgである。
蒸気の臨界点のときの圧力を臨界圧力といい、蒸気の臨界点のときの温度を臨界温度という。
この臨界圧力を超えた状態を超臨界という。超臨界の物体の物性は、一般の液体や気体とは異なる。 なお、水にかぎらず、他の分子でも超臨界の現象は存在する。二酸化炭素やメタンでも超臨界現象は存在する。 詳しくは高校の範囲を超えるので省略する。
エントロピ線図およびエンタルピ線図
[編集]

蒸気を用いた工業の熱機関の解析などで、P-v線図やT-v線図やP-T線図などでは、実用に供しない場合がある。 たとえば、P-v線図では、グラフ上の各曲線は、それぞれ温度が一定であるが、実際の気体の状態変化は温度が一定とは限らない。同様にT-v線図でも、実際の熱機関内の気体の状態変化は、圧力一定とは限らない。P-T線図も同様である。 もちろん、P-v線図などを、熱機関の解析の実務に用いる場合もある。 ともかく、P-v線図などでは都合の悪い場合があるので、代わりに、エンタルピまたはエントロピとの関係をグラフで表示した線図が用いられる場合がある。 たとえば、エンタルピ-圧力線図や、エンタルピ-エントロピ線図や、温度-エントロピ線図などが用いられる場合がある。
また、線図には湿り蒸気の性質は記載されていないので、これらの線図とは別に、数表によって湿り蒸気のエンタルピやエントロピを記載した飽和蒸気表がある。
 |
 |
 |
| 蒸気用エンタルピーエントロピー(H-S)線図 | 蒸気の圧力 - エンタルピー(p-h)線図 | 蒸気用温度エントロピー(T-S)線図 |
蒸気表
[編集]| 蒸気表 | |||||
|---|---|---|---|---|---|
| Temp. | Pressure | H of liquid | ΔvapH | ΔvapW | ρ of vapor |
| 0 °C | 0.612 kPa | 0.00 J/g | 2496.5 J/g | 126.0 J/g | 0.004845 kg/m3 |
| 10 °C | 1.227 kPa | 42.0 J/g | 2473.5 J/g | 130.5 J/g | 0.009398 kg/m3 |
| 20 °C | 2.536 kPa | 83.8 J/g | 2450.9 J/g | 135.1 J/g | 0.01728 kg/m3 |
| 30 °C | 4.242 kPa | 125.6 J/g | 2427.9 J/g | 139.7 J/g | 0.03036 kg/m3 |
| 40 °C | 7.370 kPa | 167.2 J/g | 2404.9 J/g | 144.2 J/g | 0.05107 kg/m3 |
| 50 °C | 12.33 kPa | 209.0 J/g | 2381.4 J/g | 148.7 J/g | 0.08285 kg/m3 |
| 60 °C | 19.90 kPa | 250.8 J/g | 2357.6 J/g | 153.0 J/g | 0.1300 kg/m3 |
| 70 °C | 31.15 kPa | 292.7 J/g | 2332.9 J/g | 157.3 J/g | 0.1979 kg/m3 |
| 80 °C | 46.12 kPa | 334.6 J/g | 2307.7 J/g | 161.5 J/g | 0.2931 kg/m3 |
| 90 °C | 70.10 kPa | 376.6 J/g | 2282.6 J/g | 165.5 J/g | 0.4232 kg/m3 |
| 100 °C | 101.32 kPa | 419.0 J/g | 2256.3 J/g | 169.4 J/g | 0.5974 kg/m3 |
| 110 °C | 143.27 kPa | 460.8 J/g | 2229.5 J/g | 173.1 J/g | 0.8264 kg/m3 |
| 120 °C | 198.50 kPa | 503.2 J/g | 2201.4 J/g | 176.7 J/g | 1.121 kg/m3 |
| 130 °C | 270.13 kPa | 545.8 J/g | 2172.5 J/g | 180.2 J/g | 1.497 kg/m3 |
| 140 °C | 361.4 kPa | 588.5 J/g | 2142.8 J/g | 183.2 J/g | 1.967 kg/m3 |
| 150 °C | 476.0 kPa | 631.5 J/g | 2111.8 J/g | 186.1 J/g | 2.548 kg/m3 |
| 160 °C | 618.1 kPa | 674.7 J/g | 2080.0 J/g | 188.7 J/g | 3.263 kg/m3 |
| 170 °C | 792.0 kPa | 718.5 J/g | 2047.0 J/g | 190.6 J/g | 4.023 kg/m3 |
| 180 °C | 1002.7 kPa | 762.5 J/g | 2012.2 J/g | 192.8 J/g | 5.165 kg/m3 |
| 190 °C | 1254.9 kPa | 807.0 J/g | 1975.8 J/g | 194.5 J/g | 6.402 kg/m3 |
| 200 °C | 1554.3 kPa | 851.9 J/g | 1937.3 J/g | 195.6 J/g | 7.868 kg/m3 |
| 210 °C | 1907.9 kPa | 897.5 J/g | 1897.5 J/g | 196.3 J/g | 9.606 kg/m3 |
| 221.1 °C | 2369.8 kPa | 948.5 J/g | 1850.2 J/g | 196.6 J/g | 11.88 kg/m3 |
| 229.4 °C | 2769.6 kPa | 987.9 J/g | 1812.5 J/g | 196.2 J/g | 13.87 kg/m3 |
| 240.6 °C | 3381.1 kPa | 1040.6 J/g | 1759.4 J/g | 195.1 J/g | 16.96 kg/m3 |
| 248.9 °C | 3904.1 kPa | 1080.3 J/g | 1715.8 J/g | 193.7 J/g | 19.66 kg/m3 |
| 260.0 °C | 4695.9 kPa | 1134.8 J/g | 1653.9 J/g | 190.8 J/g | 23.84 kg/m3 |
| 271.1 °C | 5603.4 kPa | 1195.9 J/g | 1586.5 J/g | 186.9 J/g | 28.83 kg/m3 |
| 279.4 °C | 6366.5 kPa | 1240.7 J/g | 1532.5 J/g | 183.3 J/g | 33.18 kg/m3 |
| 290.6 °C | 7506.2 kPa | 1302.3 J/g | 1456.3 J/g | 177.4 J/g | 39.95 kg/m3 |
| 298.9 °C | 8463.9 kPa | 1350.0 J/g | 1394.8 J/g | 172.2 J/g | 45.93 kg/m3 |
| 310.0 °C | 9878.0 kPa | 1415.7 J/g | 1307.7 J/g | 164.2 J/g | 55.25 kg/m3 |
| 321.1 °C | 11461 kPa | 1483.9 J/g | 1212.7 J/g | 154.5 J/g | 66.58 kg/m3 |
| 329.4 °C | 12785 kPa | 1537.9 J/g | 1133.2 J/g | 145.6 J/g | 76.92 kg/m3 |
| 340.6 °C | 14727 kPa | 1617.9 J/g | 1007.6 J/g | 130.9 J/g | 94.25 kg/m3 |
| 348.9 °C | 16331 kPa | 1687.0 J/g | 892.0 J/g | 117.0 J/g | 111.5 kg/m3 |
| 360.0 °C | 18682 kPa | 1797.0 J/g | 694.0 J/g | 91.0 J/g | 145.3 kg/m3 |
| 371.1 °C | 21349 kPa | 1968.3 J/g | 365.0 J/g | 47.0 J/g | 214.5 kg/m3 |
| 374.4 °C | 22242 kPa | 2151.2 J/g | 0 J/g | 0 J/g | 306.8 kg/m3 |
| Temp. | Pressure | H of liquid | ΔvapH | ΔvapW | ρ of vapor |
熱の伝わり方
[編集]機械工学では、材料内での熱の伝わる仕組みについて考える必要がある。 たとえば、自動車エンジンとかボイラとかを想像していただければ、納得していただけるだろう。
そもそも、熱とは何か。熱と温度の違いは何か。 物体を加熱すれば温度が上昇することから、熱とは、それを受け取ることによって、温度が上がるエネルギーであろう。(潜熱とか融解熱とかは、簡単化のため、しばらく、考えないことにする。) そして、熱は、外部から手を加えなければ、自然と温度の高い所から、温度の低いところへと移動していく。 その結果、温度の高かった場所は、熱を手放し、だんだんと温度は低くなる。逆に、温度の低かった場所は温度が高くなる。そして、いつしか、ふたつの箇所の温度は同じになる。 いっぽう、熱が、温度の低いところから、温度の高い所へと自然に移動することは、ない。 こうして、熱は温度の高いところにあった熱は拡散していく。 熱と温度の違いに付いては、詳しくは、物理の高校教科書などを参照していただければ、ふつうは書いてあるので、それらを参照していただきたい。
静止した物体での熱の伝わり方には、大きく分ければ、熱伝導と熱放射の二つに分けられる。
熱放射
[編集]
熱放射(thermal radiation)とは何か。実は、絶対零度以外の温度を持つ、どの物体も、電磁波を出している。その放射する電磁波が、人間の眼に見えないのは、単に放射電磁波の周波数が、人間の目の可視領域で無いからという理由である。 この放射する電磁波は、常温では周波数が低く、赤外線の領域である。高音になるほど、物体の放射電磁波の周波数が高くなり、可視領域へと入っていく。溶鉱炉などで、高温で溶けた金属が光るのは、この放射光によるものである。 この放射光もエネルギーを高温側から低温側に輸送する。 熱放射は、別名では熱輻射(ねつふくしゃ)とも言う。
熱伝導率
[編集]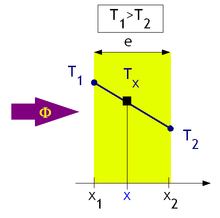
さて、熱伝導の定義では、以上のような放射光による熱エネルギの輸送とは、区別した別の定義を用いる。 熱伝導の定義を説明する。 まず、金属塊でも、木材でも何でもいいが、なんらかの固体を想像していただきたい。 このような固体の物体に、加熱などで温度差を生じさせると、分子の熱振動によって、物体内部で熱の輸送現象がおこる。この個体内部に対する、高温部から低温部への、熱の輸送を、熱伝導(heat conduction)という。 放射は、便宜上、熱伝導としては扱わない。熱伝導と放射とを区別するのは、物理学分野での、そういった定義の決まりなので、読者には、従っていただくしか無い。また、気体や液体などの流体に対しては、対流という温度差によって生じる流れが生じるので、この流体に対する熱の輸送のメカニズムは、熱伝導とは区別する。詳しくは、「熱伝達」に関する項目で解説する。
まず、個体内部の温度差に対する熱伝導の仕組みを、数式を用いて定量化しよう。
結論から話すと、以下の定義をまずは覚えて頂きたい。
- 熱流束:
物体内を移動した熱のエネルギーを、単位面積で割ったもの。記号はqで表すのが一般的。単位は[W/m2]
- 温度勾配:
材料内の2地点の、温度差を、2地点の距離で割った値。温度差をΔTとして、距離をdとすれば、 温度勾配はΔT/dである。単位は[K/m]あるいは[℃/m]である。
- 熱伝導率:
熱伝導における、熱流束と温度勾配との比例係数で、熱流束を温度勾配で割った値を熱伝導率(thermal conductivity)という。記号はλが一般。 熱伝導率の定義より、
- [W/m2]
が成り立つ。
そして、熱伝導率λは、実は物性値である。物性値とは、物質の種類によって、値がほとんど決まるという種類の値である。 さて、このような一連の定義は、本当に妥当なのか。定義そのものも、妥当性の確認を、実験的になされなければならない。このような熱伝導の公式の提唱と実験は、物理学者のフーリエ達によってなされた。 なので、このような歴史的経緯から、上記の式の、
は、フーリエの業績をたたえて、フーリエの式、あるいはフーリエの法則(Foulier's Law)と呼ばれる様になった。 このフーリエの法則の公式は、熱伝導の基本法則である。 固体内の熱伝導については、安心してフーリエの法則の公式を用いて良い。 ただし、あくまでも、「固体」内での場合である。流体については、対流現象のため、通常では、フーリエの式は使えないので、間違って流体にフーリエの式を適用しないように注意のこと。
フーリエの法則の物理的な意味について、考えよう。
まず、仮に読者が熱伝導のフーリエの法則を知らなかったとして、定式化までの再発見の道筋をたどってみよう。
熱が一方向のみに伝わるように問題設定したほうが定式化しやすいので、空間内を厚さdの平らで広い壁で遮蔽し、壁の片側を高温に熱して温度 にしたとする。壁の向こう側は温度 だとしよう。
(
>
とする。)
壁の先の温度の蓄積能力は十分に大きく、熱流による温度変化の影響は微小だとして、壁の温度を時間によらず一定としよう。壁の温度が一定でないと、熱流束が一定にならずに非定常になり解析が複雑になるので、簡単化のための、問題設定の便宜である。
フーリエら先人たちは、壁が平らでない場合での熱伝導の定式化も研究しているが、初学者には難解なので、そのような事例は、ここでは考えず、壁は平らとしよう。 壁の温度が一定でない、非定常温度の場合もフーリエは数学的解析によって研究しているが、高校レベルを超える難解な計算なので、今回は考えない。
さて、温度差があると、熱は高温から低温へと輸送されるのだった。まず2点の温度差を
とすると、この温度差に、熱の移動量は比例することになる。しかし、まだ、2点間の壁の厚さによる影響を考慮していないのである。複数個の壁を用意し、厚さの異なる壁を複数個ほど用意したとして、各壁の両側の温度差を同じにして実験をすれば、当然、壁が厚いほど、熱は移動しにくいだろう。
は、この条件を満たしている。
熱伝達率
[編集]流体については、温度差によって対流が起こるため、通常の解析では、流体での熱の伝わりの解析にはフーリエの式は使えない。読者に注意するが、間違って、流体に対してフーリエの式を用いてはいけない。 では、次に、その流体での熱の伝わりかたの仕組みを考えよう。
流体だって、固体と同じように、温度を持ってるし、温度は分子の振動だから、熱伝導は起こる。そして物性値としての熱伝導率を、気体や液体も物質であることに変わりはないから、流体も熱伝導率を持っている。 しかし、流体では対流もおこるので、流体内での温度変化が熱伝導によるものか、対流によるものか区別をしづらい。 一般の設計実務では、流体での熱の輸送に関する計算では、熱伝導のフーリエの式は用いない。 かわりに熱伝達の公式を用いる。
まず、高温の温度 の壁1番と、低温の温度 の壁2番に、流体が挟まれているとしよう。壁の大きさは、両方とも同じとしよう。両方の壁は十分に広く長いとする。簡単のため、流体は密閉されてるとしよう。断熱材と二つの壁で密閉しよう。断熱材は壁は覆わないとする。 このとき、流体を通過する熱流束qは
- [W/m2]
で表せる。ここで比例定数hは、熱伝達率(heat transfer coefficient)もしくは伝熱係数や熱伝達係数などという。hの単位は[W/(m^2・K)]である。 熱伝達率を記号hの代わりに記号αで現すこともある。 、 は流体に接している高温物体の固体の温度と低温物体の固体の温度である。 熱伝導の式と異なるところは、厚さに影響しないことである。そもそも対流が起こり、その対流の影響のほうが熱伝導よりも強いので、流体の熱伝達の式には、厚さを含めるのは不合理である。 ここで熱伝達率hは、流路の形状や流速や温度差などによって変わる値であり、物性値ではない。流体の物性によっても熱伝達率hの値は変化をするが、しかし物性以外の影響も受けて値が変化するので熱伝達率hは物性値ではない。このhの値の決め方は、装置ごとに実験による測定によって決める。 文献などを見れば、様々な条件での熱伝達率の測定結果の値が載っていたり、実験式が載っている場合があるが、その値や実験式は設計用の参考値であり、設計者にとっては推定値である。最終的に熱伝達率を正確に決定する際には、装置ごとに熱伝達率を実験で確認する必要がある。
熱通過率
[編集]熱伝導や熱伝達など、熱の移動を総称して、熱通過という。
熱伝導を行う固体と、熱伝達を行う流体とを統一的に扱えるように、熱輸送の概念が定義される。 熱伝導の公式も熱伝達の公式も、両方とも、温度差qによって熱流束が発生することには変わらないので、以下のようにして、熱輸送率kの定義式が、温度 と温度 の2点に対して定義される。
- [W/m2]
式の形は、熱伝達と類似してるが、熱輸送率の場合は、熱を伝えるものが固体か流体かは問わない。 同様に、熱を伝える仕組みが熱伝導か熱輸送かを、熱輸送率の場合は、問わない。 たとえば、平板に対して、熱輸送率を定義した場合、平板の熱輸送率kは、熱伝導率をλ、平板の厚さをdとすれば、平板の熱輸送率kは、
となる。
複数の壁を重ねた場合の熱通過率
[編集]複数の壁を重ねた場合の熱通過率を考えよう。(「熱伝導」ではなく、「熱通過」率としたのには、このほうが計算がしやすくなるという理由があるため。) まず、壁が2枚だとして、厚さ 、熱伝導率 の平らな壁1番に、厚さ 、熱伝導率の平らな壁2番を隙間なく重ねて、接触させたとしようたとしよう。壁1番と壁2番の接合面の温度は としよう。この両壁の接合部の温度 は未知数である。 そうすると、壁1番を通過した熱流束qは、すべて壁2番を通ると考えることができるので以下の式になる。
である。 そして、求めたい複数の壁を重ねた場合の熱通過率は、
である。 まず、各壁の熱伝導率の式を、熱通過率の式に変換したほうが、計算しやすいので、変換しよう。すると以下の式になる。
次のようにして、熱流束を、熱伝達率で割って、右辺を温度だけの式にする。
2式を足し合わせれば、未知数が消える。
これより
そして、q/(T_1-T_2)が、両壁を合成した熱通過率kなので、
である。
各壁の熱通過率を、壁1番の熱通過率 と、壁2番の熱通過率 とすると、合成した熱通過率を以下の形に書ける。
これより、
である。
熱伝導を行う平板が、熱伝達を行う流体に挟まれてる場合
[編集]この場合の、熱輸送率の求め方も、同様に、熱流束の式を立てて連立方程式で計算すればいい。
結果を言うと、合成の越通過率をkとして、壁の高温側の流体の熱伝達率を 、壁の厚さをdとして、壁の熱伝導率をλ、壁の低温側の熱伝達率を とすると、(温度の変数は、計算の過程で消える。)
になる。
右辺のd/λが、一項だけ他の項と違い変わって見えるかもしれないが、この項については、壁の熱輸送率を とすれば、
だから、
とも書ける。
一般には、
の式が、流体に挟まれた平板壁の合成の熱輸送率の公式として使われる。

























































