高等学校物理/原子物理
電子と光
[編集]電子の発見と測定
[編集]陰極線
[編集][図]
図のように両極に電極を封入したガラス管に高電圧を加えるとき、内部の気体を抜いていくと管全体が内部気体特有の発光を示す。このような稀薄気体による放電を真空放電という。最近は減りつつあるが、蛍光灯は真空のガラス管に少量の水銀蒸気を入れて真空放電を起こすことにより、水銀から紫外線を発生させて蛍光塗料を光らせている。
1858年、ドイツのプリュッカーは真空放電の実験の中で、ガラス管内の真空度を増すとあるとき管内の光が消えて正極側の管壁が蛍光を発することを発見した。これを受けて、1874年のイギリスのクルックスが「負極から出た何かが正極に向かって進んで管壁にぶつかることによって蛍光する」というアイディアを提唱した。ここで、正極・負極をそれぞれ陽極・陰極、陰極から出る何かを陰極線と名づけた。
その後、さまざまな実験により陰極線の性質が解明された。
- 写真フィルムを感光する
- 蛍光物質に当てると発光を示す
- 物体に遮られ、その後ろに影を作る
- 電場や磁場に、負電荷と同様の影響を受ける
- これらの性質は陰極の金属の種類や管内の気体の種類に依存しない
これらを総合すると、「陰極線は負電荷を持つある特定の粒子の流れで、その粒子はすべての金属に含まれる」という仮説が立つ。
この粒子の正体を調べるために、次のような実験が行われた。
トムソンの実験
[編集]1897年、イギリスのトムソンは陰極線が電場や磁場でどのように曲げられるかを詳しく調べた。
真空中に間隔d、長さlの平行平板電極a, bを上から順に置き、電極面に平行に、電極間に向けて左から速さvで質量m、電荷-eの荷電粒子を入射する。電極の右端から距離Lだけ離れたところに蛍光物質を塗ったスクリーンを置いて粒子の到達地点を記録する。電子の入射方向にx軸をとり、電極の左端を通りスクリーンに平行な直線をy軸とする。また、表から裏の向きにz軸をとる。粒子の質量mは非常に小さい値と考えられるので、重力の影響は無視する。
まず、極板間にy軸の負の向きに大きさVの電圧をかける。このとき、極板間の電場は一様になるので、電場の強さはと求まる。粒子は負電荷なので電場の向きと逆、すなわちy軸の正の向きに電場からの力を受け、その大きさはである。よって粒子の加速度は運動方程式よりと求まる。
このとき、x軸方向は等速直線運動、y軸方向は等加速度運動をするので、xy平面上では放物運動をすると見做せる。x軸方向で考えると、速さvでlだけ移動する時間は、きはじの法則よりである。y軸方向で考えると、粒子が電極を抜ける瞬間のy座標はと求まる。
電極を抜けた粒子は等速直線運動を行うので、粒子が電極を抜けてからスクリーンに到達する時間はx軸方向で考えるとである。y軸方向は位置に達したときの速度で等速運動をするので、 である。よって、電極を通過した後のy方向の移動距離はと求まる。スクリーンに到達したときの粒子のy座標はである。
次に、電極間にだけz軸の正方向に一様な磁場を加える。入射した粒子が直進するように磁場を調整すると、粒子が電場から受けるクーロン力と磁場から受けるローレンツ力が釣り合うので、磁束密度の大きさについて力の釣り合いの式よりが成り立つ。よってである。
これらを総合すると、よりと求まる。
このを荷電粒子の比電荷という。当時、最終的に求まった式に含まれる定数はすべて測定可能だったので、比電荷の値を求めることができた。具体的には、 C/kgである。
この比電荷は陰極に用いる金属や管内の気体の種類に依存しないので、物質の中には負電荷を持った粒子が共通に含まれることが証明された。この粒子は電子と名付けられた。現在では、この電子が電気の正体であると判っている。
なお、電子の具体的な質量や電気量の測定は1909年のミリカンの実験を待つことになる。
ミリカンの実験
[編集]ミリカンの実験とは、霧吹きなどで作成した油滴の微小な飛沫に、X線やラジウムなどで帯電させる。そして、外部から電場を印加する。すると、油滴の重力(下向き)のほかに、電場による静電気力(上向きになるように電極板を設置する)が働くので、釣り合って静止する状態になった時の電場から、電荷の値を確かめる実験である。
油滴の質量をm、電気量を-q、電場の強さをE、重力加速度をgとすると、油滴に働く重力とクーロン力が釣り合っているので、である。
電場の強さを0にすると、油滴は自由落下運動を始めるが、空気抵抗によって終端速度vで落下するようになる。このとき、油滴に働く重力と空気抵抗力が釣り合っているので、空気抵抗の比例定数をkとしてが成り立つ。
総合して、を得る。
この実験を繰り返したときに算出・測定される電荷の値が全て 1.6×10-6 Cの整数倍になったので、電子1個の電荷が 1.6×10-19 Cだと分かった。
なお、この 1.6×10-19 Cのことを電気素量(でんきそりょう)という。
現在では、電気素量の詳しい値は Cと判明している。
この値と先ほどの比電荷の値から、電子の質量は kgと求まる。
化学の電気分解の実験で、金属の電気分解の実験の時に発生する気体が帯電していることは、ラボアジエなどによって古くから知られていた。実験物理学者タウンゼントは、発生した気体のモル数と、静電誘導などによって発生した電荷の合計を測定することにより、電子1個あたりの電荷を概算した。
精度は、現代の電子の電荷とケタが同じくらいの精度で、タウンゼントは電子の電荷の測定値を得た。
光の粒子性
[編集]光電効果
[編集]- (※ 実験結果グラフを追加すること。)

負の電荷に帯電させてある金属板に、紫外線を当てると、電子が飛び出してくることがある。また、放電実験用の負極に電子を当てると、電子が飛び出してくることがある。この現象を、光電効果(こうでん こうか、photoelectric effect)という。1887年、ヘルツによって、光電効果が発見された。レーナルトによって、光電効果の特徴が明らかになった。
当てる光の振動数が、一定の高さ以上だと、光電効果が起きる。この振動数を限界振動数(げんかい しんどうすう)といい、限界振動数より低い光では、光電効果が起こらない。また、限界振動数のときの波長を、限界波長(げんかい はちょう)という。
物質によって、限界振動数は異なる。亜鉛版では紫外線でないと光電効果が起きないが、セシウムでは可視光でも光電効果が起きる。
光電効果とは、物質中(主に金属)の電子が光のエネルギーを受け取って外部に飛び出す現象のことである。 この飛び出した電子を光電子(こうでんし、photoelectron)という。
光電効果には,次のような特徴的な性質がある。
- 光電効果は、光の振動数がある振動数(限界振動数)以上でないと起こらない。
- 光電子の運動エネルギーの最大値は、当てた光の振動数のみに依存し、光の強さには依存しない。
- 単位時間あたりに飛び出す光電子数は、光の強さに比例する。
これらの性質のうち、1番めと2番めの性質は、古典物理学では説明できない。 つまり、光を、電磁波という波動の性質だけを捉えていては、つじつまが合わないのである。
なぜなら、仮に、電磁波の電界(電場)によって金属から電子が放出すると考えた場合、もし光の強さが大きくなれば、振幅が大きくなるので、電界(電場)も大きくなるはずである。
しかし、実験結果では、光電子の運動エネルギーは、光の強さには依存しない。
よって、古典力学では説明できない。
アインシュタインの 光量子仮説
[編集]上述の矛盾(古典的な電磁波理論では、光電効果を説明できないこと)を解決するために、次のような光量子仮説がアインシュタインによって提唱された。
- 光は、光子(こうし、photon)の流れである。光子を、光量子(こうりょうし)ともいう。
- 光子1個のエネルギーEは、光の振動数 に比例する。
この2つめの条件を定式化すると、
となる。
この式における比例定数hはプランク定数とよばれる定数で、
仕事関数(しごと かんすう、work function)とは、光電効果を起こすのに必要な最小のエネルギーのことである。金属の種類ごとに、決まった値である。
仕事関数の値を W とすると、光子の得る運動エネルギーの最大値 K0 について、次式が得られる。
- (1.1)
この式より、光電効果が起こる条件は hν≧W となる。これは K0≧0 に相当する。
これより、光電効果が起こる限界振動数 ν0 について、hν0=W が成り立つ。
この光量子仮説により、光電効果の1番めと2番めの性質は、容易に、矛盾なく説明できるようになった。波動は粒子のように振舞うのである。 なお、光電効果の3番めの性質から、ある場所の光の強さは、 その場所の単位面積に単位時間、飛来する光子の数に比例することが分かる。
- エネルギーの単位
電子や光子一個のエネルギーは非常に小さいので、ジュール(J)をそのまま用いると使い勝手が悪い。そのため、新たにエネルギーの単位を設定する。
真空中において電子一個を1Vで加速するときに電子が得る運動エネルギーを電子ボルト(エレクトロンボルト)という(記号:eV)。である。
例) 銅の仕事関数は4.65eV
参考: 光の波長の測定
[編集]- (※ 範囲外)
そもそも、光の波長は、どうやって測定されたのだろうか。
現在では、たとえば原子の発光スペクトルの波長測定なら、回折格子をプリズムとして使うことによって、波長ごとに分け、波長が測定されている。(※ 参考文献: 培風館(ばいふうかん)『step-up 基礎化学』、梶本興亜 編集、石川春樹 ほか著、2015年初版、25ページ)
おおまかな原理を述べると、可視光ていどの光の波長の測定は、回折格子によって測定するわけだが、ではその回折格子の細かい数百ナノメートル〜数千ナノメートルていどの間隔の格子ミゾをどうやって作るのか、という問題に行き着いてしまう。
歴史的には、下記のように、可視光の波長が測定されていった。
まず、1805年ごろの「ヤングの実験」で有名なヤングらの研究により、可視光の波長は、おおむね 100nm(10-7m) 〜 1000nm の程度であることは、この頃から、すでに予想されていた。
その後、ドイツのレンズの研磨工だったフラウンホーファーが、すぐれた回折格子を開発し、可視光の波長を精密に測定する事に成功した。フラウンホーファーは回折格子を作るために細い針金を用いた加工装置を製作し、その加工機で製作された回折格子を用いて、光の波長の測定をし始めたのが、研究の始まりである。1821年にフラウンホーファーは、1cmあたり格子を130本も並べた回折格子を製作した。[1]
また、1870年にはアメリカのラザフォードがスペキュラムという合金を用いた反射型の回折格子を製作し(このスペキュラム合金は光の反射性が高い)、これによって1mmあたり700本もの格子のある回折格子を製作した。(要出典)
さらにこのころの時代、送りねじの潤滑のために水銀を使う水銀浮遊法が、研究開発で行われた。
より高精度な波長測定が、のちの時代の物理学者マイケルソンによって、干渉計(かんしょうけい)というものを用いて(相対性理論の入門書によく出てくる装置である。高校生は、まだ相対性理論を習ってないので、気にしなくてよい。)、干渉計の反射鏡を精密ネジで細かく動かすことにより、高精度な波長測定器をつくり、この測定器によってカドミウムの赤色スペクトル線を測定し、結果の波長は643.84696nmだった。マイケルソンの測定方法は、赤色スペクトル光の波長を、当時のメートル原器と比較することで測定した。[2]
マイケルソンの制作した干渉計にも、水銀浮遊法の技術が取り入れられている、という[3]。
さらに、ネジの技術革新で、マートン・ナット(「メルトン・ナット」とも訳す)という、弾力性のある材質でネジをつくることによって誤差がならされて平均化されるので、超絶的に高精度の送りねじを作る技術が、イギリスの物理学者トーマス・ラルフ・マートン(英:en:w:Thomas Ralph Merton )などによって開発された。
なお、現代でも、研究用として干渉計を用いた波長測定器が用いられている。(要出典) メートル原器は、マイケルソンの実験の当時は長さのおおもとの標準だったが、1983年以降はメートル原器は長さの標準には用いられていない。現在のメートル定義は以下の通り。
光電効果の測定
[編集]- (※ 回路図を追加すること。)
- (※ 実験結果グラフを追加すること。)


右の実験図のように、光電管の陰極に限界振動数ν0よりも振動数が大きい光を当てると、光電子が飛び出し陽極に流れ込む。このときの電流を光電流という。
光電流の測定結果は右のグラフのようになる。
陽極の電位が正であれば飛び出した光電子は全て陽極に流れこむため、電圧を高くしても光電流の大きさは一定である。
陽極の電位が0であっても、光電子は運動エネルギーK0を持って飛び出すので、陽極に到達することができる。
陽極の電位を負にしてさらに下げると、光電子は電場から受けるクーロン力によって運動を妨げられ、ある電位 -V0で陽極に到達する前に運動エネルギーが0になってしまう。このときの電位差V0を阻止電圧といい、が成り立つ。
つまり、阻止電圧を測定すれば光電子の持つ運動エネルギーK0を求めることができる。
このとき、光の振動数νまたは光の波長λがわかっていれば、より金属の仕事関数Wも求めることができる。
ただし、陽極と陰極で金属の種類が異なるとき、これらの仕事関数の違いに伴い接触電位差が表れるため、それも考慮しなければならない。
なお、光電効果によってプランク定数を測定することもできる。
備考
[編集]太陽電池も、光電効果のような現象である。
なお、太陽電池は一般的に半導体であり、ダイオード化したPN接合の部分に光を当てる必要がある。
(PN接合部分以外の場所に、光があたっても、生じた電力を、電流として取り出せない。電流として取り出せるようにするには、PN接合の部分に、光を当てる必要がある。このため、PN接合の片方の材質を、透明か、それに近い光透過率の材料にする必要があり、「透明電極」という。
X線
[編集]X線の発見
[編集]
陰極から出た陰極線を陽極にぶつけると、ぶつかった時にX線が出る。
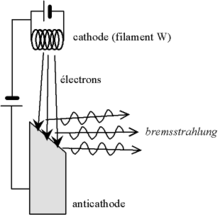
レントゲンは、1895年、放電管をもちいて陰極線の実験をしていたとき、放電管のちかくに置いてあった写真乾板が感光している事に気付いた。
レントゲンは、陰極線がガラスに当たったとき、なにか未知のものが放射されてると考え、X線と名づけた。
やがて、さまざまな実験によって、X線は次の性質をもつことが明らかになった。
- 磁場や電場で曲がらない。
この事から、X線は、荷電粒子ではない事が分かる。(結論をいうと、X線の正体は、波長の短い電磁波である。)
また、
- X線を照射された物質はイオンに電離される。(電離作用)
- 可視光線を通さない物質でも、X線なら透過できる場合がある。(医療診断に応用されている。)
- 蛍光物質を光らせる。
などの性質がある。
X線の発生とスペクトル
[編集]上のX線菅の図において、電流による発熱で陰極から放出された熱電子は高い電圧によって加速され、ターゲット(陽極)に衝突する。このとき、一個の電子の持つエネルギーの一部または全部がX線光子のエネルギーとなり、残りは陽極熱に変換される。
発生するX線のスペクトルは、ある最短の波長から始まってそれより長い波長を連続的に含む。これを連続X線という。
電子のエネルギーが全てX線光子のエネルギーに変わるとき、よりX線の波長は最短となる。このときのX線の振動数をν0、波長をλ0、加速電圧をVとすると、電子の初速度が0のとき、が成り立つ。すなわち、最短波長はと求まる。

右の図のように、連続X線の他に特定のエネルギーを持つX線が強く放射される場合があり、これを固有X線(特性X線)という。固有X線の波長はターゲットの材質で決まる。
X線の波動性
[編集]1912年、物理学者ラウエは、X線を単結晶に当てると、写真フィルムに図のような斑点の模様にあることを発見した。これをラウエ斑点(はんてん)といい、結晶中の原子が回折格子の役割をしたことで発生した干渉現象である。

1912年、ブラッグは、反射が強めあう条件式を発見した。
- (nは非負整数)
をブラッグの条件という。
上式のdは格子面の間隔の幅である。
X線の粒子性
[編集]- コンプトン効果
X線を炭素塊などの(金属とは限らない)物質に当て、その散乱されたあとのX線を調べると、もとのX線の波長よりも長いものが、散乱したX線に含まれる。 このように散乱X線の波長が伸びる現象は物理学者コンプトンによって解明されたので、コンプトン効果(またはコンプトン散乱)という。

この現象は、X線を波と考えたのでは説明がつかない。(もし仮に波と考えた場合、散乱光の波長は、入射X線と同じ波長になるはず。なぜなら、水面の波に例えるなら、もし水面を棒で4秒間に1回のペースで揺らしたら、水面の波も、4秒間に1回のペースで周期を迎えるのと、同じ理屈。) さて、波動の理論でコンプトン効果を説明できないなら、粒子の理論で説明をすれば良いだろう。
この当時、アインシュタインは光量子仮説にもとづき、光子はエネルギーhνをもつだけでなく、さらに次の式で表される運動量pをもつことを発見している。
物理学者コンプトンは、この発見を利用し、波長λのX線を、運動量 とエネルギーを持つ粒子(光子)の流れと考え、 X線の散乱を、この光子が物質中のある電子と完全弾性衝突をした結果と考えた。
- コンプトンはこの考えに基づき、光子と電子の衝突前の運動量和とエネルギー和が衝突後も保存されると仮定して計算して、実験結果と良く合うあう結果が得られることを発見した。

この図を見ると、あたかも真空中をただよう電子に電磁波を照射したように見えるが、そうではない。コンプトン効果の発見された1920年代の当時には、まだ、空中に電子をただよわせて精度よく電磁波を照射する技術など、無い。実際にコンプトンが行った実験は、石墨の炭素などの物質にX線を照射する実験である。図中の電子は、炭素などの分子が提供する電子である。
コンプトン本人の論文に、このような感じの図が書かれており、それでこのような図が普及したものと思われる。
解法は、下記のとおり。
- エネルギー保存の式を立てる。
- そして、運動量の保存の式を立てる。具体的には、x軸方向の運動量の保存の式と、y軸方向の運動量の保存の式を立てる。
エネルギー保存の式
- (1.2a)
運動量保存の式
- x軸: (1.2b)
- y軸: (1.2c)
上記の3つの式を連立し、この連立方程式を解くためにvとφを連立計算で消去させていき、のときに が得られる。
この式が実験式とよく一致するので、コンプトンの説の正しさは実証された。
- コンプトン効果の連立方程式の具体的な解法
(編集者へ: 記述してください。)(Gimyamma より。解法を書いてみました。)
式(1.2a),(1.2b),(1.2c)から、とを消去して、 の関係式を求めればよい。
- ⅰ)まず、式(1.2b),(1.2c)からを消去する。
- 式(1.2b)から
- 式(1.2c)から
- この両式を加えると
- この右辺を整頓すると、所望の
- (1.2d)
を得る。
- ⅱ)式(1.2d)を式(1.2e)に代入してvを消去する:
式(1.2a)の右辺の第2項を変形して式(1.2d)を代入する。
これを式(1.2a)の右辺に代入すると
両辺をで割ると
- (1.2e)
を得る。 この式の右辺の第2項の括弧内を次のように変形する。
この式を式(1.2e)の右辺第2項に代入すると
この式の右辺の第1項を移行し、式を変形すると
両辺にを掛けると
- (1.2f)
X線の散乱では、なので
- は、波長に比べて非常に小さい値になり無視できる。
故に式(1.2f)から
- (1.2g)
これで、所望の式が導出された。
粒子の波動性
[編集]物質波
[編集]フランスのド・ブロイは、波と考えられてた光が粒子の性質をもつならば、きっと電子も粒子としての性質だけでなく、電子も波動のように振舞うだろうと考えた。
そして、電子だけでなく、一般の粒子に対しても、その考えを適用し、次の公式を提唱した。
- 質量m、速さvの粒子は波動性をもち、その波長は次式で与えられる。
これはド・ブロイによる仮説であったが、現在では正しいと認められている。
この波は、物質波(material wave)と呼ばれる。ド・ブロイ波(de Broglie wave length)ともいう。 すなわち、光子や電子に限らず、あらゆる物質は粒子性と波動性をあわせ持つといえる。
この物質波という説によると、もしも電子線を物質に当てれば、回折などの現象が起きるはずである。
1927年〜1928年にかけて、デビッソンとガーマーは、ニッケルなどの物質に電子線を当てる実験を行い、X線回折と同様に電子線でも回折が起きることを実証した。日本でも1928年に菊池正士(きくち せいし)が雲母片に電子線を当てる実験により回折が起きることを確認した。
電子線の波長は、高電圧をかけて電子を加速して速度を高めれば、物質波の波長はかなり小さくできるので、可視光の波長よりも小さくなる。
そのため、可視光では観測できなかたった結晶構造が、電子波やX線などで観測できるようになった。生物学でウイルスが電子顕微鏡で観測できるようになったのも、電子の物質波が可視光よりも大幅に小さいからである。
粒子と波動の二重性
[編集]- 電子ビームによる波動性の干渉実験



電子銃(でんしじゅう)という実験装置がある。銃といっても、べつにSFのような兵器ではなく、電子銃とは単に電子を放出するだけの装置である。
さて、この電子銃をもちいて、1個づつ電子を当てる実験を、二重スリットを使って実験すると、図のように、波動のように、電子の多く当たった場所と電子の少なく当たる場所との縞模様ができる。
このように、電子にも粒子性と波動性があり、電子は粒子でありつつ、二重スリットに向かって電子を撃ち込むと干渉を起こすという波動性も持っている。
上述のような、さまざまな実験の結果から、すべての物質には、原子ていどの大きさの世界(以降、単に「原子スケール」などと略記する)では、波動性と粒子性の両方の性質をもつと考えられている。
このことを粒子と波動の二重性という。
光学顕微鏡(レンズを用いる顕微鏡)では、回折が起こることによって光の波長よりも小さな物体を見ることが非常に困難となる。分解能(2点を識別できる限界の距離)は10-7m(100nm)程度である。
より高い分解能を得るため、光よりも波長が短い電子線を用いる電子顕微鏡が発明された。電子顕微鏡では、加速電圧を高くすることで高い分解能を得られる。ただし、電磁波によるレンズ作用を用いることによる収差(像の歪み)などの障碍から、現在の最高分解能は10-10m(0.1nm)ほどに留まっている。
この分解能では、ウイルスどころか金属・酸素などの原子すらも観察することが可能であるが、中性子・陽子・電子などは小さすぎて観察できない。
副読本:朝永振一郎『光子の裁判』1949年(朝永振一郎は1965年にノーベル物理学賞を受賞した物理学者だが、寺田寅彦と同様に一般向けの書籍を多数執筆する文豪でもあった。この作品では、光子になぞらえた「波乃光子」という被告の裁判を舞台に、粒子と波動の二重性の不思議さを繙いている。)
- 不確定性原理

不確定性原理の主要な提唱者である。
そして、原子スケールでは、ある一つの物質(主に電子のような粒子)について、その位置と運動量の両方を同時に決定する事はできない。このことを不確定性原理(ふかくていせい げんり)という。
原子・原子核・素粒子
[編集]原子
[編集]陰極線に関連する実験から、全ての原子に負の電荷を持つ電子が含まれると考えられたが、原子は電気的に中性なので正の電荷を帯びた部分が存在するはずである。
そこで、原子の構造について様々な説が登場した。
比電荷の測定を行ったトムソンは、一様に正に帯電した球の中を電子が運動しているというプラムプディングモデル(ブドウパンモデル)を提唱した。長岡半太郎は、フランスのジャン・ペランが提唱した、正電荷を持つ粒子の周りを電子が公転している土星型モデルを定量化して大幅に補強した。しかし、実際に採択されたのは以下のようなモデルだった。

ドイツのガイガーとニュージーランドのマースデンは、ラザフォードの研究室において(ラジウムから出した)α粒子をうすい金箔に当てる実験を行い、α粒子の散乱の様子を調べた。(なお、α粒子の正体はヘリウムの原子核。)その結果、ほとんどのα粒子は金箔を素通りするが、金箔中の一部の場所の近くを通ったα粒子だけが大幅に散乱する現象を発見した。
α粒子は電子の7000倍以上の質量を持つことから、電子の影響で大きく曲げられたとは考えにくい。そこで、原子内の狭い部分に集中した正電荷がα粒子に強い斥力を及ぼし、その部分が原子の質量の大部分を占めていると考えて計算を行い、実験結果をうまく説明することに成功した。
原子(10-10)内の正電荷が集中した10-15~10-14程度の重い部分は原子核と名付けられた。
原子は、中心に原子核があり、そのまわりを電子が運動するというラザフォードモデルとよばれるモデルによって説明される。ラザフォードモデルは、土星型モデルを発展させたものとも言える。
- ラザフォードモデル
原子(atom)は、全体としては電気的に中性であり、負の電荷を有する電子を電子殻に持つ。 ここで、ミリカンの実験 による結果などから、電子の質量は水素イオンの質量の約1/1840程度しかないことが分かっている。 すなわち、原子は電子と陽イオンとが含まれるが、質量の大部分は陽イオンがもつことが分かる。 原子核の大きさは原子全体の1/10000程度であるため、原子の大部分は真空である。 原子核は、正の電荷をもつZ個の陽子(proton)と、電気的に中性な(A−Z)個の中性子(neutron)からなる。 陽子と中性子の個数の合計を質量数(mass number)という。 陽子と中性子の質量はほぼ等しいため、原子核の質量は、質量数Aにほぼ比例する。
統一原子質量単位
[編集]原子の質量は極めて小さいため、キログラム(kg)をそのまま用いるのは不便である。そこで、(同位体を除いて)118種類ある原子のうちどれかを基準として考えたい。ここで、他の様々な原子と化合できるため質量比較がしやすいこと、同位体13Cなどの存在比が極めて小さいことなどから、炭素原子を基準にするのが適当である。
12C原子一個の質量を12と定義する単位系を統一原子質量単位という。単位はDa(ダルトン)であるが、廃止されたamu(アトミックマスユニット)を用いる人もいる。
化学基礎で原子量を習ったが、原子質量単位は質量を表す単位なのに対し、原子量は質量そのものでなく質量比を表しているので単位はなく無次元である。混同しないように注意しよう。
水素原子のスペクトル
[編集]高温の物体から発光される光には、どの(可視光の)色の波長(周波数)もあり、このような連続的な波長の光を連続スペクトルという。
いっぽう、ナトリウムや水素などの、特定の物質に電圧がかけられ放電したときに発光する波長は、特定の数本の波長しか含まれておらず、このようなスペクトルを輝線(きせん)という。
パルマーは、水素原子の数本ある輝線の波長が、次の公式で表現できることに気づいた。
- (2.1)
上式中の「m」はメートル単位という意味。(上式のmは代数ではないので、間違えないように。)
その後、水素以外の原子や、可視光以外の領域についても、物理学者たちによって調べられ、次の公式へと、物理学者リュードベリによって、まとめられた。
- (2.2)
上式のRはリュードベリ定数といい、/mである。
量子論と原子の構造
[編集]
ラザフォードの原子模型に従えば、電子は、まるで惑星の公転のように原子核を中心とする円軌道の上を一定の速度で運動する。
- 円運動する質点は加速度をもつので、このモデルの電子は加速度運動を続けることになる。
- ところが古典電磁気学で、加速度運動をおこなう電荷は電磁波を放出して、エネルギーを失うという法則が既に発見されていた。
- この法則によれば、原子核の周りをまわる電子は電磁波を放出し続け、エネルギーを絶えず減らしていく。それにつれて電子は原子核に向けて落下していくため、原子核との距離を小さくしながら原子核の周りを回転し、やがて原子核に衝突してしまう。円軌道の上を安定的に運動することは不可能なのである。
- デンマークのボーアはラザフォードの原子模型の深刻な矛盾を克服し、さらに水素原子の放出する線スペクトルについても説明できる原子模型を作るため、
- プランクの提唱したエネルギー量子化の考えとアインシュタインの光量子論を取り入れた大胆な仮説を立てた(1913年)。
- 仮説1;量子条件
原子核を中心とする半径rの円軌道を速さvで回転する電子の軌道角運動量はの正整数倍しかとりえない,すなわち
- (2.3)
を満たさねばならない(角運動量の量子化)。この状態を定常状態,この条件を量子条件という。
- ここで、m[kg]は電子の質量を、hは プランク定数である。
- このボーアの式の正整数nを量子数(りょうしすう)という。
後年(1924年)、ド・ブロイは「物質粒子は波動性を持ち、その波(物質波)は、波長
をもつ」と提唱した。また,(2.3)を変形すると
- .
これらは電子の軌道一周の長さが電子の物質波の波長の正整数倍のとき,電子波は定常波になることを示している。
- これは、円軌道上に定常波ができるための条件と同じである。
- ※ 検定教科書でも、ボーアの式の表記は、速度vをつかって表される表記である。
- 仮説2;振動数条件
電子はあるきまったとびとびのエネルギーしか持たない。このとびとびのエネルギー値をエネルギー順位という。
- 電子がエネルギー順位をからに遷移する(エネルギーを失う)ときには、できまる振動数の一個の光子を放出し、
- 逆にエネルギー順位Eの電子が外部からエネルギーを得ると、エネルギー順位E'に遷移する。
エネルギー準位
[編集]
水素原子において、電子軌道上にある電子のエネルギーを求める計算をするが、まず、そのためには、原子の半径を求める必要がある。
- 半径
水素の電子が原子核を中心とする半径rの円軌道上を一定の速度vで運動しているとすれば、運動方程式は
で表される。
一方、電子が定常波の条件を満たす必要があるので、前項の式(1)から、
である。
このvをさきほどの円運動の式に代入して整頓すれば、
(ただし、n=1, 2 , 3 ,・・・)
になる。こうして、水素原子の電子の軌道半径が求まる。
さきほどの軌道半径の式でn=1のとき半径r1をボーア半径という。
- エネルギー準位
原子の世界でも、運動エネルギーKと位置エネルギーUの和が、エネルギーである。
位置エネルギーUは、この水素の電子の場合なら、静電気エネルギーを求めれば充分であり、電位の式によって求められて、
となる。
運動エネルギーKは、なので
上式の右辺第一項に、
- 円運動の方程式の両辺にrを掛けた
を代入すれば、
となる。
さらに、これに電子の軌道半径の式(3)を代入すれば、
となる。これが水素原子のエネルギー準位である。
エネルギー準位の公式をよく見ると、まず、エネルギーが、とびとびの値になることが分かる。また、エネルギーが負になる事がわかる。
n=1のときが、もっともエネルギーの低い状態であり、そのため、n=1のときが安定な状態である。よって、電子は通常、n=1の状態になる。
なお、
- に諸定数の値を入れて計算すると
- となるので、
- 水素原子のエネルギー順位は
- と書ける。
- は、約 13.6 eV になるが、これは水素のイオン化エネルギーの値である。これは、実験値にも、よく一致する。
水素原子のスペクトルの経験式の理論的導出
[編集]水素原子の発する光のスペクトルの実測値を表すリュードベリの経験式については、既に「水素原子のスペクトル」の項でで説明した。
- ボーアの水素原子モデルに基づいて得られたエネルギー順位と振動数条件の仮説を用いれば、この式が以下のように理論的に導出できる。
- 任意の正整数m、n(>m)を考える。
- すると、振動数条件の仮説により
電子がエネルギー順位から、低いエネルギー順位に遷移するときに、振動数 の光子を一個放出する。
- この光子の波長λは
で与えられるので、右辺のエネルギー順位に式(4)を代入すると
が得られる。 で、リュードベリ定数Rを定義すると、式(5)は
Rの定義式中の諸定数に値をいれて計算すると
驚くべきことに、リュードベリの経験式が、見事に導出できたのである。 これは、ボーアの仮説の妥当性を示すものと言えよう。
- (※ 範囲外: 大学の範囲) 実際の特性スペクトルの波長は、原子内部の電子の影響により、若干、ズレる。そういった内部電子の補正を考慮した、より精度の高い式として「モーズリーの公式」というのが知られている。なお歴史的な順序は、上述の説明の順序とは逆である。じつは先にモーズリーの式が発見され、あとから、モーズリーとは別に独立に研究されていた上述のようなボーアやラザフォードの理論を用いると、モーズリーの公式もうまく説明できるという事が物理学者コッセルによって発見された[5]。なおモーズリーの公式について調べたいなら、大学科学の量子化学などの科目名の教科書に記載があるだろう。
基底状態と励起状態
[編集]エネルギー準位の式において、n=1のときエネルギーが最低である。この状態を基底状態という。n=2, 3, …となるにつれ、電子の起動が外側へ写ってエネルギーが大きくなる。これらの状態を励起状態という。
高温の炎中にある種の金属粉末や金属化合物を置くと、試料が熱エネルギーによって解離し原子化される。それぞれの原子は熱エネルギーによって電子が励起され、外側に存在する高エネルギーの電子軌道へと移動する。励起された電子が安定な基底状態に戻ろうとする際に、余分なエネルギーを電磁波として放出する。電磁波の周波数が、ちょうど可視光線の範囲に入る場合が有る。このとき、炎色反応として肉眼で観察できる。
なお、原子の電子軌道のエネルギーは連続した値ではなく飛び飛びの値であるため、励起された電子が基底状態に戻る際に放出されるエネルギーも連続した値ではない。このため、炎色反応として放出された光は連続スペクトルではなく輝線スペクトルを示す。また、元素によっても電子軌道のエネルギーはある程度決まるため、元素によって特徴的な輝線スペクトルを示す。これが、炎色反応を示す元素の種類により、炎色反応によって放出される光の色が決まる理由である。
- フランク・ヘルツの実験
[図] ドイツのフランクとヘルツは、気体放電での電子の働きを調べるため、水銀蒸気を封入した図のような装置で実験を行った。
フィラメントFから飛び出す電子を、Fと網目状のグリッドGとの間に加える電圧Vで加速する。Gの後ろに電極Pを置き、Pに到達した電子の数を電流計で調べる。GP間にはFG間と逆向きに僅かな電圧(0.5V程度)を加え、電子がGに到達しても運動エネルギーが0に近ければPに到達できなくした。FG間の電圧を上げながらPに到達する電子の数を調べ、[グラフ]のような実験結果を得た。
[グラフ]
電子の数は電圧の増加とともに増すが、4.5~5V付近をピークに減少し、再び増加する。その後、約4.9Vの間隔で同様の増減を繰り返す。また、4.9eVに相当する波長のスペクトルも発生していた。
ボーアは、この実験結果を「4.9eVは水銀原子の基底状態と励起状態のエネルギーの差であり、電子の運動エネルギーが加速電圧で4.9eVに達した時に水銀原子が励起して電子が運動エネルギーを失う」と説明した。
その後、FG間から波長2.537×10-7(4.9eVのエネルギーに相当)の紫外線が発生していることが確認された。これは、励起された水銀原子が基底状態に戻る時にそのエネルギー準位の差に相当する波長の光子を放出して生じたものと考えられ、原子には離散的な値のエネルギー準位が存在するというボーアの仮説が実験で裏付けられた。
なお、固有X線の発生原理もエネルギー準位で説明することができる。
原子核
[編集]原子核の構造
[編集]原子核は、陽子と中性子からできている。二つを総称して核子という。 陽子は正電荷をもち、中性子は電荷をもたない。
原子核の陽子同士はクーロン力によって反発し合うが、陽子と中性子を結ぶ核力がクーロン力よりも強いため、それが核子同士を繫ぎ止めている。
- (※ 範囲外:) 原子番号の低い元素において、陽子と中性子の個数は、ほぼ同数である場合が多い。たとえば、酸素や窒素では、陽子と中性子は同数である。一方、元素番号の高い元素ほど、陽子よりも中性子が多く、たとえばウラン235は中性子数が陽子数の1.5倍である。これには核力の性質が関係していると考えられている[6]。
なお、陽子と中性子は核子と呼ばれる。
ある元素の原子核の陽子の数は、周期表の原子番号である。
また、陽子と中性子の数の和は質量数とよばれる。
質量数Aの原子核は非常に強い核力のために、小さな球体状の空間の中に固まっており、その半径rは、 ~ であることが知られている。
同位体
[編集]同じ元素でも、中性子の数が異なる原子がある。これらを互いに同位体(アイソトープ)という。例えば、水素に対する重水素・三重水素、酸素に対するオゾンなどがそうである。水素の原子核は陽子1つであり、重水素(D)の原子核を重陽子、三重水素(T)の原子核を三重陽子という。また、重水素からなる水分子を重水という。
一般に、同じ元素であれば同位体でも化学的性質は同一である。しかし、物理的性質は大きく異なる場合がある。
原子の質量は、イオン化した原子を加速して電場・磁場が軌道にもたらす影響を調べることで求められる。
トムソンは、電場と磁場を加えた空間にイオンを入射させ、比電荷の同じイオンがスクリーン上の同じ放物線上に集まるような装置を制作した。これにより、ネオンの同位体が発見された。
トムソンの研究室にいたイギリスのアストンは、トムソンの装置を基にイオンの速さにかかわらず比電荷が同じであればスクリーン上の一点に集まるような装置(質量分析器)を製作した。この装置により多くの同位体が発見され、それらの質量と存在比も精密に測定された。
放射能と放射線
[編集]元素の中には、放射線(radiation)を出す性質をもつものがあり、この性質を放射能(radioactivity)という。 また、放射能をもつ物質は放射性物質といわれる。放射能を持つ同位体を放射性同位体という。 放射線には3種類存在し、それぞれα線、β線、γ線という。
α崩壊は、親原子核からα粒子が放射される現象である。α粒子の正体はヘリウム原子核である。α崩壊後、親原子核の質量数は4小さくなり、原子番号は2小さくなる。
β崩壊は、親原子核の中性子が陽子と電子に変化することで、電子が放射される現象である。なお、放出された電子はβ粒子ともよばれる。β崩壊後、親原子核の質量数は変化しないが、原子番号は1増加する。
γ線は、α崩壊またはβ崩壊直後の励起状態にある原子核が、よりエネルギーの低い状態に遷移するときに放射される(かつてはγ崩壊と呼んだが、原子核が崩壊していないので廃止された)。γ線の正体は光子で、X線より波長の短い電磁波である。
α崩壊やβ崩壊によってもとの原子核の数は徐々に減っていくが、これらの崩壊は原子核の種類ごとに決まった一定の確率で起きるので、崩壊によってもとの原子核の数が減る速度は原子核の個数に比例して変化する。しかし、崩壊によってもとの原子核の数が半減するのにかかる時間は、原子核の種類だけによってきまる。そこで、この時間のことをその原子核の 半減期(はんげんき、half life ) と呼ぶ。崩壊によって原子核の個数がどれだけになるかは、この半減期を用いて記述することができる。原子核の半減期をT、時刻tでの原子核の個数をN(t)とすると、
が成り立つ。
放射線に関しては様々な単位が用いられる。
かつてはキュリー、エルグ、ラド、レントゲン、レムなどの単位が用いられていたが、現在ではSI単位系に沿って以下の単位が用いられる。(ただし、現在でも前述の単位を用いる場合がある)
| 物理量 | 単位 | 記号 | 説明 |
|---|---|---|---|
| 放射能の強さ | ベクレル | Bq | 原子核が毎秒一個の割合で崩壊するときの放射能の強さを1Bqとする。 |
| 照射線量 | クーロン毎キログラム | C/Kg | 放射線の照射によって0℃、1013hPaの空気1cm3あたりに3.335641×10−10 C(1 |
| 吸収線量 | グレイ | Gy | 1Kgの物質が放射線の吸収と共に1Jのエネルギーを得たときの吸収線量を1Gyとする。 |
| 線量当量 | シーベルト | Sv | 吸収線量に、放射線の種類ごとに定められた人体の障害の受けやすさを表す線質係数(修正係数)を掛けたもの。例えば等価線量を求めたいなら放射線荷重係数を掛け、実効線量を求めたいならさらに組織荷重係数を掛ける。 |
| 線量率 | シーベルト毎時 | Sv/h | 単位時間あたりに受ける放射線の量 |
ちなみに、1キュリーは37GBq(37ギガベクレル、370億ベクレル)に等しい。
生体が放射能を受けることを被曝という。※「被爆」表記は意味が違うので絶対用いないように。
放射線は電離作用を持つので生物細胞に影響を及ぼし、遺伝子を破壊することで癌を発症させたり奇形を発生させたりする。被曝量が大きい場合には急性の障碍を引き起こすこともある。この影響を最小限にするには、放射線源から離れる、浴びる時間を短くする、鉛で放射線を遮るなどの対策が必須である。一方で、自然界には放射線がありふれている。普段の生活では食事による内部被曝や宇宙線による被曝などで年間2.4mSvほどの放射線を自然界から受けている。これらは被曝量が少ないため人体に害はない。また、放射線は非破壊検査、癌治療、レントゲン撮影、農作物の品種改良などの分野で応用されている。
手塚治虫は、自著『火の鳥』の「未来編」にて栽培促進に利用される放射線と、そこにおける事故を描いている。1967年の時点で既に放射線の産業利用の可能性と事故が起こったときの重大性を読み取っていたのである。
なお、福島原発事故の処理水放出が取り沙汰されているが、あれは国際基準よりも厳しい基準で安全性を確認してから放出しているため、一部が騒いでいるような汚染ではない。
発展:半減期公式の導出
[編集]原子核の崩壊速度は、原子核の個数に比例すると述べた。実は、上に述べた公式はこの情報だけから純粋に数学的に導き出すことができるものである。高等学校では扱わない数学を用いるが、興味のある読者のためにその概要を記しておく。
原子核の個数と崩壊速度の間の比例定数は原子核の種類によって決まる。この定数をその原子核の崩壊定数という。崩壊定数がλの原子核の時刻tでの個数をN(t)とすると、その変化速度、すなわちN(t)の微分は、
で表される。このような、ある関数とその微分との関係を表した式を微分方程式といい、微分方程式を満たすような関数を求めることを、微分方程式を解くという。(詳しい解法は解析学基礎/常微分方程式で説明するが、)この微分方程式を解くと
が得られる。(この式が確かに先ほどの微分方程式を満たしていることを確かめてみよ)
半減期Tとは、となるtのことなので、先ほどの式から
が得られる。よって、
が得られる。
原子核反応
[編集]
霧箱(きりばこ)という、蒸気のつまった装置をつかうと、なんらの粒子が通過すると、その粒子の軌跡で、気体から液体から凝着が起きるので、軌跡が、目に見えるのである。(イメージ的には、飛行機雲のようなのを、イメージしてください。) で、磁場を加えた場合の、軌跡の曲りぐあい等などから、比電荷までも予想できる。
- 陽子の発見
ラザフォードは、窒素ガスを密閉した箱にα線源があると、正電荷をもった粒子が発生することを発見した。
この正電荷の粒子が、陽子である。つまり、ラザフォードは陽子を発見した。
同時に、酸素も発生することを発見し、その理由は窒素が酸素に変換されたからであり、つまり、原子核が変わる反応も発見した。
これらのことを式にまとめると、
である。
このように、ある元素の原子が、別の元素の原子に変わる反応のことを 原子核反応(核反応)という。また、上のような反応式を核反応式という。
化学反応では原子の種類が変わらずその組合せが変わるだけであったが、核反応では別の種類の原子が生まれる。
正電荷を持つ二つの原子核の間には電磁気力により斥力が働く。核反応は、2つの原子核がこの斥力に打ち克って核力が働く近距離に近づいた時に初めて起こる。そのため、核反応を起こすには大きな運動エネルギーが必要であり、そのためにサイクロトロン・ベータトロン等の加速器が用いられる。
一般に、核反応では反応の前後で質量数の和と電気量の和は保存されることがわかっている。
- (※ 範囲外: )霧箱は、種類にもよるが、普通、エタノールまたはアルゴンの気体が封入される[7]。
- 霧箱のような実験装置の用途として、陽子の実験の用途のほか、原子核反応の回数を観測する目的でも使うことが出来る。放射線の測定器のいわゆる「ガイガーカウンター」の原理も、霧箱と類似している。原理的な放射線測定器であるガイガー・ミュラー管には気体(アルゴンやエチレンガスなどの不活性な気体)が封入されている。霧箱のように気気体を封入した測定管に、高電圧をかけた電気極板を追加することで、放射線をとらえるようにしたものがガイガー管である[1]。物理学者ガイガーは、このような測定器を開発し、さらに原子核反応によって生成されるヘリウム分子を集めて気体として封入し、(※ wiki補足: そのヘリウムに気体の状態方程式などを適用する事により、)当時としては最高水準の精度でアボガドロ定数を測定する事に成功した[8]。当時知られていた、プランクの熱輻射の理論から算出されるアボガドロ定数の値や(ボルツマン定数 Na k と気体定数 k の比からアボガドロ定数 Na が求められる)物理学者ベランがブラウン運動から求めたアボガドロ定数に、ガイガーのアボガドロ定数の精度は匹敵する精度であった[9]。
- 中性子の発見
ラザフォードは1920年頃に既に陽子と同じ質量で電気的に中性な粒子の存在を予言していた。1930年、ドイツのボーテがポロニウムから放出されるα線をベリリウムに当てると透過力の強い放射線が出ることを発見し、翌年にキュリー夫妻がこれをパラフィン(アルカンのうち炭素数が20以上のもの。水素を多く含む。)に当てると陽子が飛び出すことを発見した。夫妻は放射線をγ線と考えてコンプトン効果で説明しようと試みたが、非現実的な仮定を余儀なくされて頓挫した。イギリスのチャドウィックはこの放射線をヘリウムや窒素に当て、これを電荷を持たず陽子とほぼ等しい質量の粒子の粒子線と考えると辻褄があうことを示し、1932年に論文を提出した。この粒子は中性子、放射線は中性子線と名付けられた。
- 質量とエネルギーの等価性
原子核は、それを構成する核子である陽子と中性子が自由であるときの質量の和より、小さい質量をもつ。この減った質量を、質量欠損と呼ぶ。 質量数A、原子番号Zの原子核の質量欠損を、式で書けば, 原子核の質量をm、陽子と中性子の質量をそれぞれとしたとき、
- である。
- (※ 範囲外: )原子にもよるが、一般に質量欠損の大きさは、1%程度[10]である。
陽子と中性子が核力によって結合すると、その結合エネルギーに等しいエネルギーのガンマ線が放出される。アインシュタインの特殊相対性理論によれば、質量mとエネルギーEには、
という関係がある。
エネルギーと質量の等価性によれば、陽子と中性子が結合したときに放出されるγ線のエネルギーに等価な質量が減ることになるが、これが原子核の質量欠損である。

そもそも、どうやって原子や分子の質量を精度よく測定するか?
一般に原子レベルの質量測定法として精密科学でよく知られるものとして、右図のような、磁場によって荷電粒子を曲げる方式のものがある。このような磁場とローレンツ力を用いた方式による質量測定は一般に、「磁場偏向型」といわれる。
このような装置により、磁場や電化の大きさは実験的に決定できるので、曲率が質量の関数になるので、つまり半径から質量が逆算できる。
測定対象の元素材料が中性の原子であっても、その原子が固体なら、それに電子ビームを当てて、電子によって弾き飛ばされた材料が帯電してイオン化しているので、それから、上記のような磁場による質量測定が可能になる。
なお、化学の同位体の存在やその質量も、このころ、このような装置で発見された。
なお(高校では習わないが)、原子質量がいくつもの元素で測定できるので、派生的に、まず
化学の理論で分かる原子番号Zと原子量Aと、測定された原子の質量の測定値Mをもとに、
Z,AからMを求める公式が作成された(ワイツゼッカーの公式。1935年)。
また、原子半径の予想値なども算出されていった(レインウォーター(人名)。1953年)。
このことから、陽子と中性子がバラバラに存在する時よりも、纏まって原子核を構成しているときの方がエネルギーが質量欠損分だけ小さいことがわかる。逆に、原子核をバラバラの核子にするにはのエネルギーを与える必要がある。この意味で、を結合エネルギーという。化学で扱った結合エンタルピーは原子と分子の話であったが、こちらは核子と原子核の話である。
質量数Aは核子の数なので、核子一つあたりの結合エネルギーはと表される。これの値は軽い原子核の領域で急激に増大し、鉄が最も最大となる。故に、核反応においては鉄が最も安定な元素である。
- 核エネルギーと核分裂
核反応では、原子核の質量の和が反応の前後で変化する。質量和が減少する場合、その差が核エネルギーとなる。このとき、結合エネルギーの和は増大し、核エネルギーは結合エネルギー和の変化量に等しい。一回の化学反応で解放されるエネルギーは数eV程度であるのに対し、一回の核反応で解放されるエネルギーは数MeVを超える。例えば、リチウム7と水素が衝突してヘリウム2つになる核反応では、1.68×1012Jという厖大なエネルギーが発生する。これは石油40トンを燃やして得られるエネルギーに相当する。
ドイツのハーンとシュトラスマンは、ウランに中性子を照射したときの反応性生物の中に、ウランとほぼ半分の質量を持つバリウム141などの原子核が含まれることを発見した。このように、一つの原子核がいくつかの原子核に分かれる反応を核分裂という。ウランのように質量数が多い原子核は、一つの原子核でいるよりも二つの原子核に分裂した方がエネルギー的に安定である。これが核分裂の起こる原因である。
核分裂は歴史的には原子爆弾に利用された。日本は原子爆弾を実戦使用された唯一の国である。
現代では、核分裂は原子力発電所で使用されている。
ウラン235やプルトニウム239を核燃料とし、熱運動する気体分子と同程度の速さの中性子を衝突させると様々な壊れ方の核分裂が起こる。このとき、いずれの場合も200MeV程度のエネルギーが解放され、2、3個の速い中性子が出る。この速い中性子を減速材(水や重水など)に衝突させて減速することで、別の核燃料に衝突させやすくする。このようにして次々に核分裂が起こることを連鎖反応という。原子力発電は、核分裂で発生した熱エネルギーでタービンを回して発電している。中性子を吸収する制御棒を用いることで核分裂が爆発的に起こらない且つ停止しないように制御している。連鎖反応が持続的に保たれる条件がちょうど満たされるとき、「原子炉は臨界にある」という。臨界状態では中性子数は一定に保たれる。原子炉の稼働は臨界点の近くで行われている。少ない燃料では中性子が核反応することなく散逸するので、臨界にあるための核燃料の量に下限があり、これを臨界量という。
原子力発電は再生可能エネルギーの一つに数えられていて、発電量は他の方式に比べて圧倒的であるが、安全対策や放射性廃棄物の処理などの問題がある。 2011年の東日本大震災では地震そのものには余裕で耐えたものの、津波により電源がロストしたことで炉心の冷却機能が失われて炉心融解(メルトダウン)が起こり、爆発とともに莫大な量の放射性物質が散布される、という事故が発生した。原子力発電の稼働にあたっては、このような重大事故に対する厳重かつ多重の安全対策が必須である。(w:福島第一原子力発電所事故も参照。)
また、核分裂により生じる放射性元素の中には半減期が数百万年にも及ぶものが含まれ、これらの処理をどのように行うかも重要な課題である。
なお、原子力発電には沸騰水型と加圧水型の2種類がある。
- 核融合
必要があれば高等学校地学も参照。
恒星では原子核同士が衝突することで質量数の大きな原子核が生まれている。このように、より大きな質量数の大きな原子核ができる反応を核融合反応という。 軽い原子核が核融合を起こすとき、結合エネルギーが増加し、その差のエネルギーが解放される。
太陽の中では、4個の水素原子核(陽子)から幾つかの段階を経て1個のヘリウム原子核が生成されている。このとき、約27MeVのエネルギーが解放される。
太陽は水素と核融合により生じるヘリウムから構成されており、水素が尽きると寿命を迎える。しかし、太陽よりも質量の大きな星ではヘリウムも核融合反応を起こして炭素が生成される。中心温度が15億Kを越えていれば炭素も核融合反応を起こしてネオンが生成し、その後は十分な質量があればネオン→酸素→珪素→鉄と核融合反応が進行する。鉄はこれ以上核融合反応を起こさないのである時点で恒星は寿命を迎え、超新星爆発を起こす。このとき、さらなる反応によりニッケル・金などのさらに重い元素が生成される。
初期の宇宙には水素・ヘリウム・リチウムあたりの軽い元素しか存在しなかったと推定され、長い年月で様々な恒星で核融合反応が進行することによって他の元素が十分量生成されてきたと考えられている。
核融合は核分裂とほぼ同時代に発見されたが、連続的に発生させるには数億℃の環境が必要であることから、当初はあまり注目されなかった。
核融合反応自体は短時間ながらも地上で起こすことに成功している。例えば、原子爆弾の進化系である水素爆弾は、原子爆弾の爆発により生まれる膨大な熱エネルギーを利用して核融合反応を起こすことによって原爆の威力を更に高めている。史上最強の水素爆弾ツァーリ・ボンバの爆発では、2.1×1017Jものエネルギーが放出されたとされている。
現在では、核融合発電の実用化が盛んに研究されている。核融合発電は核分裂を利用した従来の原子力発電に比べて圧倒的に安全でコストパフォーマンスも良いが、核融合反応の安定的な持続に未だ成功していないので、お目にかかれるのはまだ先である。
素粒子
[編集]

まず、宇宙線の観測により、μ粒子というのが、発見されている。
範囲外: どうやって素粒子を観測するか
[編集]そもそも、どうやって素粒子を観測するかというと、いくつかの方法があるが、
- 写真乾板。(素粒子観測用の乾板を「原子核乾板」という)
- 霧箱
などが使われた。
霧箱
[編集]霧箱は、過飽和状態の水蒸気を利用して、荷電粒子が通過した際に水滴が凝結し、その軌跡を可視化する装置である。
磁場を加えた場合の、軌跡の曲りぐあい等などから、比電荷までも予想できる。
このように、霧箱をつかった実験により、20世紀前半〜中盤ごろには、いろいろな粒子が発見された。
μ粒子以外にも、陽電子が、霧箱によって発見されている。
反物質
[編集]まず、陽電子という物質が1932年に鉛板を入れた霧箱(きりばこ)の実験でアンダーソンによって発見されており、陽電子は質量が電子と同じだが、電荷が電子の反対である(つまり陽電子の電荷はプラスeクーロンである)。(※ 鉛板については高校の範囲外。)
そして、電子と陽電子が衝突すると、2mc2のエネルギーを放出して、消滅する。この現象(電子と陽電子が衝突すると2mc2のエネルギーを放出して消滅する現象)のことを、対消滅(ついしょうめつ)という。
陽子に対しても、反陽子がある。反陽子は、電荷が陽子と反対だが、質量が陽子と同じであり、陽子と衝突すると対消滅をする。
中性子に対しても、反中性子がある。反中性子は、電荷はゼロだが(ゼロの電荷の±を反対にしてもゼロのまま)、質量が同じで、中性子と対消滅をする。
陽電子や反陽子や反中性子のような粒子をまとめて反粒子といい、反粒子で構成された物質を反物質という。
対消滅と逆に、γ線などから粒子と反粒子のペアが生成されることを対生成という。真空中であっても真空の揺らぎによって対生成・対消滅が絶えず起こっている。
現在の宇宙においては反物質は少量しか存在しないが、宇宙の黎明期には物質と同程度存在し、対消滅によってその殆どが消えたと考えられている。あるいは、宇宙の未知の領域に反物質のみで構成された領域も存在するという仮説が立っている。
(※ 範囲外: )放射性同位体のなかには、崩壊のときに陽電子を放出するものがある。最先端の病院で使われるPET(陽電子断層撮像法)技術は、これを応用したものである。フッ素をふくむフルオロデオキシグルコースという物質は癌細胞によく取り込まれる。PET診断では、これに(フルオロデオキシグルコースに)放射性のフッ素 18F をとりこんだ放射性フルオロデオキシグルコースを用いている。
μ粒子
[編集]
反物質とは別に、μ粒子が、宇宙線の観測から、1937年に見つかった。
このμ粒子は、電荷は、電子と同じだが、質量は電子の約200倍である。
なお、μ粒子にも、反μ粒子という、反物質が存在することが分かっている。
- μ粒子などの素粒子を検出するために、写真乾板を使う。通常の写真乾板とは違い、粒子線のような細かいものを捕らえられるように調整されており、「原子核乾板」という。(「原子核乾板」については範囲外。)
- 乾板中の成分にμ粒子が当たることで、電気化学的な反応が起こり、乾板が反応する。
- 早い話、X線とX線乾板の原理と同じような原理で、μ粒子を使った(火山などの)内部研究が行われてた。近年は、原子核乾板の代わりに、半導体センサーを使って、検出している(要するに、デジカメの光センサーなどと同じ原理)。
- μ粒子の発生方法
このような観測に使われるμ粒子をどうやって発生させるのか?
宇宙線から飛んでくるμ粒子をそのまま使うという方法もありそれを実行している研究者もいるが、それとは別の手法として、加速器などで人工的にμ粒子などを発生させるという方法もある。
加速器を使った方法は、下記の通り。
まず、シクロトロンやサイクロトロンを使って、電子などを超高速に加速させ、それを一般の物質(グラファイトなど)に当てる。
すると、当然、いろんな粒子が発生する。
そのうち、π中間子が、磁気に反応するので、大きな電磁石コイルで、π中間子を捕獲する。
このπ中間子が崩壊して、μ粒子が発生する。
※ 範囲外: 宇宙線の発生原因は不明
[編集]そもそも宇宙線が何によって発生しているかの発生原因は、現時点の人類には不明である。(※ 参考文献: 数研出版の資料集の『図説物理』)
超新星(ちょうしんせい)爆発によって宇宙線が発生するのでは、という説もあるが、とにかく宇宙線の発生原因については未解明である。
範囲外?: スピン
[編集]電子や陽子や中性子などは、「スピン」という磁石のような性質をもっている。磁石にN極とS極があるように、スピンにも、2種類の向きがある。スピンのこの2種類の向きは、「上向き」と「下向き」に、よく例えられる。
全分子は、電子や陽子や中性子を含むのに、なのに多くの物質が、あまり磁性を発生しないのは、反対符号のスピンをもつ電子が結合しあうことで、打ち消しあうからである。
中学高校で観測するような普通の方法では、スピンが観測できないが、分子などの物質に磁気を加えつつ高周波を加えるなどすると、スピンの影響によって、その分子の振動しやすい周波数が違うなどの現象をもちいて、間接的に(電子などの)スピンを観測できる。(なお、核磁気共鳴法(NMR、nuclear magnetic resonance)の原理である。 ※ 理論的な解析は、大学レベルの力学の知識が必要になるので省略する。) 分子中の水素原子や、ある種の放射性同位体(中性子がたった1個ふえただけの同位体)など、高周波の影響を受けやすく、その理由のひとつが、スピンによるものだと考えられてる。(※ なお、医療で用いられるMRI(magnetic resonance imaging)は、この核磁気共鳴法(NMR)を利用して人体内部などを観測しようとする機器である。)
さて、実は素粒子も、スピンをもつのが普通である。
μ粒子はスピンをもつ。
μ粒子の「スピン」という性質による磁気と、μ粒子の透過性の高さを利用して、物質内部の磁場の観測方法として既に研究されており、このような観測技術を「μオンスピン回転」という。超伝導体の内部の観測などにも、すでに「μオンスピン回転」による観測が研究されている。
陽子と中性子のアイソスピン
[編集]陽子と中性子は、質量はほとんど同じである。電荷が違うだけである。
そして、電子と比べると、陽子も中性子も、質量がかなり大きい。
この事から、「陽子や中性子にも、さらに中身があり、別の粒子が詰まっているのでは?」という疑問が生まれてきて、陽子や中性子の内部の探索が始まった。
まず、陽子と中性子の内部構造として、架空の素粒子を考えられ、陽子と中性子は、それらの素粒子の状態が違うだけ、と考えられた。
いっぽう、電子には、内部構造がない、と考えらている。
され、20世紀なかば、量子力学では、そのころ、すでに、電子の状態として「スピン」という概念が、みつかっていた。
スピンの2種類の状態は、「上向き」「下向き」というふうに、よく例えられる。
このような量子力学を参考にして、陽子と中性子でも「アイソスピン」という概念が考えられた。
陽子と中性子は、アイソスピンの状態が違うだけ、と考えられた。
クォーク
[編集]その後、20世紀半ば頃から、「アイソスピン」を発展させた「クォーク」という理論が提唱された。
架空の「クォーク」という3個の素粒子を仮定すると、実在の陽子や中性子の成り立つモデルが、実験結果をうまく説明できる事が分かった。
電荷()をもつ素粒子「アップクォーク」と、±()をもつ素粒子「ダウンクォーク」があって、
- で陽子、
- で陽子、
と考えると、いろいろな素粒子実験の結果をうまく説明できる事が分かった。
なお、電子には、このような内部構造はない、と考えられいる。
アップクォークは「u」と略記され、ダウンクォークは「d」と略記される。
陽子のクォーク構造はuudと略記される(アップ、アップ、ダウン)。
中性子のクォーク構造はuddと略記される(アップ、ダウン、ダウン)。
加速器実験と中間子
[編集]なお、上記の説明では省略したが、おおよそ1950〜60年代ごろまでに、高山での宇宙線の観測や、あるいは放射線の観測や、またあるいはサイクロトロンなどによる粒子の加速器衝突実験により、陽子や中性子のほかにも、同程度の質量のさまざまな粒子が発見されており、それら新種の粒子は「中間子」に分類された。
そもそも、「クォーク」の理論は、このような20世紀半ばごろまでの実験や観測から何百個もの新種の粒子が発見されてしまい、そのような経緯があったので、クォークの理論が提唱されたのである。
さて、「中間子」(ちゅうかんし、mason メソン)とは、もともと理論物理学者の湯川秀樹が1930年代に提唱した、陽子と中性子とを引き付けているとされる架空の粒子であったが、20世紀なかばに新種の粒子が発見された際、「中間子」の名前が使われることになった。
さて、実験的に比較的早い時期から発見された「中間子」では、「π中間子」がある。ある種類のπ中間子は、アップクォークと反ダウンクォークからなり、π+と略記される。(ダウンクォークの反物質が、反ダウンクォーク。) π+=
別のある種類のπ中間子は、ダウンクォークと反アップクォークからなり、πーと略記される。π-=
このように、ある粒子内のクォークは合計2個のであっても良い場合もある。(かならずしも、陽子のようにクォーク3個でなくてもかまわない場合もある。)
(※ このような実験例から、粒子内に合計5個のクォークや7個のクォークを考える理論もあるが、しかし高校物理の範囲を大幅に超えるので、説明を省略。)
また、中間子は、自然界では短時間のあいだだけ、存在できる粒子だという事も、観測実験によって、分かってきた。(中間子の存在できる時間(「寿命」)は短い。すぐに、他の安定な粒子に変換してしまう。)
第2世代以降の素粒子
[編集]しかし、アップとダウンだけでは、説明しきれない粒子が、どんどんと発見されていく。クォークの提唱時の当初は、おそらく、 「クォークのアップとダウンで、きっと、ほとんどの中間子の構造を説明できるだろう」 と期待されていたのだろうが、しかし、宇宙線から1940年代に発見された「K中間子」の構造ですら、アップとダウンでは説明できなかった。
このほか、加速器の発達などにより、アップとダウンの組み合わせだけで説明できる数を超えて、どんどんと新種の「中間子」が発見されてしまい、もはやアップとダウンだけでは、中間子の構造を説明しづらくなってきた上、μ粒子が、説明できない。
また、加速器実験により、1970年代に「D中間子」など、さまざまな中間子が、実験的に実在が確認された。
このように、アップとダウンだけでは説明のできない、いろいろな粒子が存在することが分かり、そのため、素粒子理論では、「アップ」(u)と「ダウン」(d)という2種類の状態の他にも、さらに状態を考える必要に、せまられた。そして、新しい状態として、まず「チャーム」(記号c)と「ストレンジ」(記号s)が考えられた。加速器実験の技術が発展し、加速器実験の衝突のエネルギーが上がってくると、さらに「トップ」(記号t)と「ボトム」(記号b)というのが考えられた。
なお、μ粒子には内部構造はないが、陽子や中性子に電子を対応させるのと同様に(第1世代)、チャームやストレンジからなる陽子的・中性子的な粒子とμ粒子を対応させた(第2世代)。同様に、トップやボトムからなる粒子にμ粒子を対応させた(第3世代)。
| 種類 | 電荷 | 第1世代 | 第2世代 | 第3世代 |
|---|---|---|---|---|
| クォーク | アップ (u) | チャーム (c) | トップ (t) | |
| ダウン (d) | ストレンジ (s) | ボトム (b) | ||
| レプトン | 電子(エレクトロン) (eー ) | μ粒子 (μー ) | τ粒子 (τー ) | |
| 電子ニュートリノ(νe ) | μニュートリノ(νμ ) | τニュートリノ(ντ ) |
電子やμ粒子は内部構造をもたないと考えられており、レプトンというグループに分類される。

用語
[編集]素粒子の観点から分類した場合の、陽子と中性子のように、クォーク3個からなる粒子のことを、まとめてバリオン(重粒子)という。π中間子(π+=)など、クォークが2個の粒子は、バリオンに含まない。
陽子と中性子やラムダ粒子などといったバリオンに、さらに中間子(中間子は何種類もある)を加えたグループをまとめて、ハドロンという。
なお、普通の物質の原子核では、陽子と中性子が原子核に集まっているが、このように陽子と中性子を原子核に引き合わせる力のことを核力という。
ともかく、バリオンには、核力が働く。通説では、中間子にも、核力は働くとされている。つまり、ハドロンに、核力が働く。
ハドロンは、そもそもクォークから構成されている事から、「そもそもクォークに核力が働くのだろう」的な事が、考えられている。
現在の物理学では、クォークが単独では取り出せていないのと同様に、グルーオンも単独では取り出せてはいない。
さて、物理学では、20世紀から「量子力学」という理論があって、この理論により、物理法則の根源では、波と粒子を区別するのが無意味だと言われている。そのため、かつては波だと考えられていた電磁波も、場合によっては「光子」という粒子として扱われるようになった。
グルーオンも、クォークとクォークを引き付ける力を、量子化したものであろう。電荷との類推で、クォークにも色荷(カラー荷)というのが考えているが、その性質は、あまり解明されてない(少なくとも高校で教えるほどには、まだ充分には解明されていない)。
グルーオンのように、力を媒介する粒子のことをゲージ粒子という。
| 力の種類 | ゲージ粒子 | 相対的強さ | 到達距離 | 力の源 |
|---|---|---|---|---|
| 電磁気力 | 光子(フォトン) (電磁場を量子化したもの) |
10-2 | ∞ | 電荷 |
| 強い力 (クォークを引き付けあう力のこと。) |
グルーオン | 1(基準) | 10-15m | 色荷 |
| 弱い力 (β崩壊を司る「力」のこと) |
ウィークボソン(W粒子、Z粒子) | 10-5 | 10-17m | 弱荷 |
| 万有引力(重力) |
重力子(グラビトン) (未発見) |
10-38 | ∞ | 質量 |
重力を媒介する架空の粒子のことを重力子(グラビトン)というが、まだ発見されていない。
電磁気力を媒介する粒子は光子(フォトン)という。
なお、光子もゲージ粒子に含める。
つまり、光子やグルーオンは、ゲージ粒子である。
β崩壊をつかさどる力のことを弱い力といい、この力を媒介する粒子をウィークボソンという。
グルーオンの媒介する力のことを強い力という。
歴史的にはハドロンを素粒子に含めた時代もあり、その時は素粒子が数百種類を数えていた。現在では、素粒子はクォーク(アップ、ダウン、チャーム、ストレンジ、トップ、ボトム)、レプトン(エレクトロン、エレクトロンニュートリノ、μ粒子、μニュートリノ、τ粒子、τニュートリノ)、ゲージ粒子(フォトン、グルーオン、W粒子、Z粒子、グラビトン)、ヒッグス粒子の17種類であるとされている。
発展:力の統一
[編集]現代物理学において、自然界に存在する力はすべて電磁気力・弱い力・強い力・重力の4つに統一されている。
これらの力は宇宙誕生時は一つの力だったと考えられており、現在この4つの力をさらに統一しようとする試みが行われている。
電磁気力と弱い力を統一する電弱統一理論は既に完成しており、ワインバーグ=サラム理論の名で1979年にノーベル物理学賞を受賞している。電弱統一理論は、ヒッグス粒子の発見によって理論が裏付けられた。強い力と電弱統一理論を統一する大統一理論は未完成ではあるものの、裏付けとなる現象の観測待ちとなっている。
3つの力と重力を統一する超大統一理論は万物の理論と呼ばれ、さまざまなアプローチで構築が進められているが、ある一つの大きな問題が存在する。
それは、重力は他の力に比べて圧倒的に弱いという事実である。日常生活で考えてみると、磁石で鉄をくっつけられることから「巨大な地球の重力がかなり小さい磁石の電磁気力に負けている」と気がつくことができる。
重力が弱い理由はいくつか考えられているが、その中でも有名なものは「重力子が他の素粒子が到達することのできない次元方向に拡散しているため」という仮説である。これは素粒子を質点でなく大きさをもつ一次元の弦(あるいは二次元以上の膜)とみなし、素粒子の種類の違いを振動の仕方の違いに対応させる超弦理論という理論の研究の中で生まれた仮説である。素粒子の種類の違いを表現するには我々の住む三次元空間では振動方向が足りないことから、「この世界は本当はもっと高次元な空間である」との仮説が生まれ、その中で唱えられ始めた。超弦理論の一つであるM理論では、「この世界は十次元空間と一次元時間の十一次元時空間であり、余剰次元は小さく丸まっている(コンパクト仮説)」という方向で理論が構築されている。なぜ重力子のみが余剰次元方向に拡散できるかについては、「他の素粒子は開いた弦でありこの三次元空間に張り付いているが、重力子は閉じた弦であって空間に縛られない」という仮説が立っている。
この仮説では重力のみが弱い理由を合理的に説明できているが、重力子が未だ未発見であること、光子すらも届かない余剰次元空間の存在を確認する手段がないことが難点である。
とりあえず、万物の理論として2024年現在最も有力視されている理論がM理論である。これ以上の深入りは避ける。
※ 範囲外: コバルト60のベータ崩壊と「弱い力」
[編集]コバルト60を極低温に冷却し、磁場をかけて多数のコバルト原子の電子殻の孤立電子スピンの方向をそろえた状態で、コバルト60がベータ崩壊して発生するベータ粒子の出る方向を調べる実験が、1956年にアメリカで行われた。
実験の結果、コバルト60がベータ崩壊してベータ粒子の出てくる方向は、コバルト60のスピンの磁気の方向と逆の方向に多く放出されているのが観測された。これは、崩壊の確率が異なっており、ベータ崩壊の対称性が敗れていることになる。
このような実験事実により、「弱い力」は非対称である。
脚注・参考文献など
[編集]- ^ 『現代総合科学教育大系 SOPHIA21 第7巻 運動とエネルギー』、講談社、発行:昭和59年4月21日第一刷発行発行
- ^ 川上親考ほか『新図詳エリア教科辞典 物理』、学研、発行:1994年3月10日新改訂版第一刷、P.244 および P.233
- ^ クリス・エヴァンス 著、橋本洋・上野滋 共訳『精密の歴史』、大河出版、2001年11月28日 再版、185ページ
- ^ 原島鮮『初等量子力学』(裳華房、2014年第40版、初版は1972年)
- ^ 山本義隆『原子・原子核・原子力』、岩波書店、2015年3月24日 第1刷、140ページ
- ^ 山本義隆『原子・原子核・原子力』、岩波書店、2015年3月24日 第1刷、190ページ
- ^ 山本義隆『原子・原子核・原子力』、岩波書店、2015年3月24日 第1刷発行、P80
- ^ 山本義隆『原子・原子核・原子力』、岩波書店、2015年3月24日 第1刷発行、P81
- ^ 山本義隆『原子・原子核・原子力』、岩波書店、2015年3月24日 第1刷発行、P82
- ^ コトバンク『日本大百科全書(ニッポニカ)の解説』(坂東弘治、元場俊雄)など























































































































