高等学校物理/物理I/運動とエネルギー/運動の法則
力の性質
[編集]力とは
[編集]力(ちから、英語:force)とは、物体を動かしたり、変形させたりする原因である。 力はベクトルで表わされる量であり、単位には ニュートン (記号 N )を用いる。
1ニュートンの大きさの定義とは、質量 1kg の物体に力を加えた時に、1m/s2の加速度を生じさせる力の大きさを1ニュートンと定めている。質量の大きい物体ほど、速度を変化させるのに、より大きな力が必要である。つまり質量とは、加速度の変化のしにくさを表す量である。
中学では、「1ニュートンは、約100gの重さ」と習うが、高校では、後述するように力を正確に考えるため、高校では、重さによる力の定義は、用いない。なぜなら、月と地球では重力の大きさが違うので、もし「重さ」によって力を定義してしまうと、場所によって力の大きさの基準が違うので、不合理である。高校では、質量と加速度にもとづいて、「力」を定義する。
- 質量とは何か
では、質量(しつりょう、mass)とは何か? 中学で習ったように「質量」を考えてよい。 月と地球では、重力の大きさが違うので、「重さ」(weight)と「質量」(mass)とは、異なる概念である。 しかし、分銅で測れば、月でも地球でも、同じ質量を測れる。
2019年にキログラムの定義が改定され、『キログラム (記号は kg) は質量のSI単位であり、プランク定数 h を単位 J s (kg m2 s−1 に等しい)で表したときに、その数値を6.62607015×10−34 と定めることによって定義される。ここで、メートル及び秒は、それぞれ c 及びΔνCsを用いて定義される。』となった。
このニュートンという単位は、既に知られている[s],[kg],[m]を用いてかくことが出来る 単位である。実際には
- [N] = [kg] [m/s]
が得られる。この関係は以降の節で扱う運動方程式(うんどうほうていしき、equation of motion)に従う。
質量 m [kg] の物体に掛かる重力の大きさ W [N]は、次のように表される。
この式において、 g は重力加速度であり、単位は[m/s2]。
- (参考 単位系の国際標準化)
昔は、製造業の機械工業などでは、力の単位に、ニュートンの他にも、
力の単位をニュートン単位に統一した理由は、昔は国や業界ごとに物理量で用いる単位が別々であり、不便であったので、その不便を解消しようと国際的な取り決めがなされたからである。その国際的な取り決めによって、力の単位にはニュートンを用いることが決まり、質量の単位にはグラムまたはキログラムを用いることが決まり、重さと質量とを区別することが決まったのである。
また、この国際的に取り決めた単位系を
また、国際単位系では、長さの単位にはメートルやミリメートル、センチメートルといったメートル法を用い、時間の単位には秒を用いる。
(※ 参考) 速度などの秒の記号は検定教科書では小文字「s」である。たとえば秒速の記号は m/s である。1時間、2時間などの「時間」の記号は h である。時速なら km/h がよく使われる。しかし「分」については、漢字のまま「分」で書くことが検定教科書でも許されている[1]。
高校入学から先の、高校や大学での理科の学習では、物理量の単位系には、原則としてSI単位が用いられる。物理学の科目だけでなく、生物や化学や地学などでも、単位系は、特別な理由が無いかぎりはSI単位系およびSI併用単位(リットル L や角度 °や1時間 h など)を用いるのが普通である。
(※参考) メートル m やキロメートルkm、キログラム kg やグラム g、 秒 s 、電流のアンペア A などが SI単位である。
(※ 参考) なお、リットルの大文字 L および小文字 l は SI単位 ではないが、しかしSIと併用される「SI併用単位」としてリットルは認められている。慣習的には、小文字 l が数字のイチとまぎらわしいので、大文字 L が使われることが多い[2]。
※ 高校生が理科のテストの答案を書く際などにSI単位やSI併用単位などについてよく分からければ、高校理科の検定教科書やふつうの受験参考書にある単位を使用すればいい。
力の測り方
[編集]フックの法則
[編集]-
フックの法則。
力は伸びに比例する。 -
フックの法則。
ばね を考えれば分かると思うが、一般に物体は形を変えるような力が働いたとき、形を戻そうとする力を働かせる。 このように元の形に戻ろうとする性質を弾性(だんせい、elasticity)という。また弾性による復元力を弾性力(elastic force)と呼ぶ。弾性力の向きは、加えた力とは反対向きである。ばね の場合、弾性力の向きは、伸びの向きとは反対向きである。
なお、ばね に力がかかってないときの元々の長さのことを、「自然の長さ」あるいは自然長(しぜんちょう)という
多くの固体の物体は、物体に加える外力が小さい場合には弾性を示す。 弾性力の大きさは、伸び(または 縮み)の長さに比例する。この比例係数(伸びと弾性力の比例係数)は、物質によって異なる。
弾性力の式は、伸びを x[m] とすると、弾性力 F[N] の大きさは、次の式で表せる。
これをフックの法則(Hooke's law)と呼ぶ。

物体が ばね であれば、比例定数 k [N/m] を ばね定数 という。
高校の段階では、物体が ばね でなくとも、弾性力をしめす物体について、この係数 k を「ばね定数」と読んでも構わないだろう。(いくつかの検定教科書でも、そのように記述している。) なお、単位 N/m は ニュートン毎メートル (ニュートンまいメートル)と読む。
- 参考: 塑性(そせい)
いっぽう、粘土(ねんど)のように容易に形を変えることが出来る物質も存在する。このような形を変えられる性質を「塑性」(そせい,plastic)という。普通科高校の教科では「塑性」を扱わないので、塑性については説明を省略する。 このように、弾性力の有無および弾性力の強さは、物質によって大きく変わる物質の性質である。
力のつりあい
[編集]力の合成
[編集]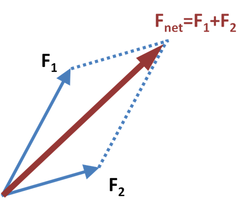
ここで、ある物体に対して、2つの力
および
が働くときに、その力は互いに足し合わされ、物体には合計で
だけの力が働くとする。 このように力はベクトルとしての加法則を満たすのである。
2つ以上の力を足しあわせて1つの力と見なすとき、その足し合わせた結果の力を合力(ごうりょく、resultant force)という。
また、合力を求めるために力を足しあわせることを「力の合成」(composition force)などという。
特に大きさが等しく向きが反対向きであるとき2力の合計はベクトルとして 0になり、物体に力が働いていない状態と等しくなる。このような状態を 力がつりあっているという。
- 3つ以上の力の合成
- (※ 図を追加してください。)
についての作図は、まずを作図し、 そして を作図すれば良い。
どの順番から作図しても答えは同じで、 を作図しても、答えは同じである。
- 問題
ある物体に、(I)x方向に[N]、y方向に[N]の力が それぞれ独立に働いているとする。 このとき、この物体には合計でどれだけの力がどの方向に働いているか計算せよ。 また、(II)それぞれの力の向きがどちらもx軸方向、 (III)片方がx軸方向でもう片方が(-x)軸 方向、 (IV)もしくは片方がx軸方向で、もう片方がx軸から測って反時計回りに 60の方向のときにどのような力を受けているかを計算せよ。
- 解答
(I) ベクトルの加法を用いると得られる力は
となる。これは、方向がx軸から測って反時計回りに45だけ回転した方向に 等しい力で大きさは
に等しい力である。
(II) 同様にベクトルの加法を用いると、
となる。これは向きはx軸方向で大きさは2fの力である。
(III) ベクトルの加法を用いると、
となる。これは力が働いていない状態である。
(IV) ベクトルの加法を用いると、
となる。これはx軸から見て30方向の力で、力の大きさは
に等しい。
力の分解
[編集]
力の合成の作業とは逆に、1つの力を2つの力に分解できる。分け方は無数にあるが、1つ目の力を決めると、平行四辺形の法則により、もう一方の力は自動的に決まる。
力のつりあい
[編集]ある物体に いくつかの力が 同時に はたらいていて、その合力が 0 のとき、「これらの力はつりあっている」とか「つりあいの状態である」などという。
2力のつりあい
[編集]
2力がつりあうためには、同一作用線上で、逆向きで、力の大きさが等しい、という3つの条件が必要である。
この3つの条件が成り立つ時、静止していた物体はそのまま静止し続け、運動していた物体はそのまま同じ速度で運動しつづける。
「逆向きで、力が等しい」という条件を式で書けば、
となる。 F2を移項すれば、
である。
※ 数学について
は 零ベクトル(ゼロベクトル) といい、大きさがゼロのベクトルのことであり、向きは無い。
3力のつりあい
[編集]
関係式
が成り立つ。
x成分、y成分、それぞれ、次の関係式が成り立つ。
作用・反作用の法則
[編集]
人が ばね を引いているとき、同時に ばね も人を引いている。 このように、物体Aに物体Bが力を加えるとき、相手の物体Bからも物体Aに同じ大きさの力が及んでいる。 このように、物体はお互いに力を及ぼしあっている。また、その及ぼしあう2つの力の向きは、逆向きである。また、それぞれの力は、同じ作用線の上にある。
このようなお互いに及ぼしあう2つの力のうち、一方の力を作用(さよう、action)といい、もう一方の力を反作用(はんさよう、reaction)という。 たとえば物体Aから物体Bに及ぼす力を「作用」とすれば、物体Bから物体Aに及ぼす力は「反作用」になる。
- 物体Aから物体Bに力Fを及ぼしているとき、同時に、物体Bからも、大きさの等しい力で、反対方向の力が、同一作用線上で、及んでいる。
これを 作用反作用の法則 (運動の第三法則)という。(高校生は、「作用反作用の法則が、第何番目だったか?」は覚えなくてよい。)
運動の法則
[編集]慣性の法則
[編集]物体は外部から力が働かない限り、その速度を変えることはない。静止していた物体は、外部から力が働かない限り、静止し続ける。(自由落下運動に関しては、重力が働いているので、物体には外部から力が掛かっている。)静止している物体の速度は速度v=0だと考える
運動している物体は、外部から力が掛からない限り、その速度を保ち続ける。(摩擦による速さの低下に関しては、摩擦力が物体に生じているので、これは外部から力が働いてることになる。)
物体が静止していたにせよ、動いていたにせよ、どちらにせよ、物体は外部から力が働かない限り、その速度を変えることはない。 これを運動の第一法則という。
物体の運動の、このような性質を慣性(かんせい、inertia)と言うので、この法則は慣性の法則(law of inertia)という。
運動方程式
[編集]理論
[編集]を運動方程式(うんどう ほうていしき)といい、物体に加わる力と、その力のよって生じる加速度の関係は、運動方程式で表される。
なお、2つ以上の力が加わるときは、たとえば2つの力の場合は、
である。
本節の以降の文で、運動方程式を証明する。
一般に、静止している物体が動きだすには、力を受けることが必要なことが知られている。

実験をするには、たとえば図のように、台車を ばねばかり で、一定の力で引っ張れば良い。それを、自動記録紙で記録する。
-
台車実験の実験結果をv-tグラフ化したもの。(模式図)
-
台車実験の実験結果をa-mグラフ化したもの。(模式図)
実験の結果によると、全ての物体は
ある一定の力[N]を受けたとき、加速度[m/s2]の大きさは、物体の受けた力に比例し、また、物体の持っている質量[kg]に反比例をする。
この法則を式で表せば、比例係数をk1として、
これを運動の第二法則である。
この第二法則を力を基準に書き換えれば、比例係数をk2として、
と表わせる。 ここで、比例係数k2の大きさが1になるように、力の定めた単位が力の単位の N(ニュートン)である。ニュートン単位の記号は N である。 1N (1ニュートン) の力の大きさの定義とは、質量1kgの物体に力を加えた時に、1m/s2の加速度を生じさせる力の大きさを 1N と定めている。
Nと、m(メートル)、kg(キログラム)、s(秒)との関係は、
- N = kg ・m/s2
である。
ニュートン単位を用いた力と質量と加速度との関係の方程式
を運動方程式(うんどうほうていしき、equation of motion)と言う。
複数の力が加わっている場合は、たとえば2つの力の加わる場合は、単に力を合成すればいいだけなので
となる。
- 例1
例えば、ある一定の力fを一様に受けている 質量mの物体は、運動方程式に従うと、 加速度
の等加速度直線運動をする。
- 例2。 重力
ある質量 m 物質が、重力 mg を受けて自由落下する場合、その物質の運動方程式を表そう。 空気抵抗を無視すれば
- ma = mg
である。 よって、両辺からmを割れば、
- a=g
であり、質量によらず、つねに自由落下する物体は、重力加速度 g で等加速度運動することが分かる。
空気抵抗がある場合は、おもに物理 II の範囲なので、説明を省略する。空気抵抗の場合の計算も簡単なので高校2年程度でも可能だが、物理Iでは他にも単元があり、他に勉強しないといけないことが多くあるので、空気抵抗のある場合を、物理 II に回そう。
おもりの引き上げ
[編集]
右の図のように質量mの おもり を加速度aで引き上げる場合、運動方程式は
- ma=T-mg
となる。ただし、それぞれの代数の向きは右図のように取った。
- (※ 未記述)
例題: 定滑車をふくむ運動
[編集]
水平で滑らかな机の上に、質量 M[kg] の台車がある。その台車に ひも がつながれ、滑車を介して、ひも の先に質量 m[kg] の おもり が釣り下げられている。
この場合の、加速度の式を求めよ。なお、重力加速度を g とする。 また、ひも が台車を引く力の大きさを求めよ。
なお、たるんでいない、軽い ひも による力の性質として、ひも による力は、ひも の 両端で、同じであるという性質がある。 なので、台車を引っ張るひもの力の大きさが T ならば、おもりを引き上げる ひも の力の大きさも同じく T になる。
また、このTのような、ひも が何かを引っ張る力のことを張力(ちょうりょく)という。
解法

運動方程式は、台車の式 と おもりの式 を、それぞれ別に、式を立てる。
まず、台車については、加速度の向きは、物体の動く右向きを正とする。 球については、鉛直下向きを正とする。
ひも が台車を引く力大きさを T とする。
台車の水平方向の運動方程式は
台車の鉛直方向の力の影響については、机からの垂直抗力で打ち消されるため、無視できる。また、滑らかな机を考えているので、摩擦の影響も無視できる。
おもりの鉛直方向の運動方程式は
では、加速度 a を先に求めるとする。そのためには、式を連立して、張力 Tを消去すればよいので、おもりの式の T に Ma を代入すれば、
となる。
移項して加速度aについて、まとめて、
よって、
- (答え)
また、ひも が引く力の大きさ T (張力)は、先ほど求めた加速度の結果の式を、台車の式 に代入すればよく、 代入すると、
となる。 よって、
- (答え)
である。
例題: アトウッドの器械
[編集]
右図のように、ひもの両端に、質量mと質量M( 仮定: 不等式 m<M が成り立つとする)のおもりを、滑車を介して、図のように釣り下げたとする。そして、手で、 おもり の両方を支えながら、静止させとするとする。 反動をつけず、ゆっくりと手を離したとする。
このときの加速度 a と、張力 T を求めよ。
- 解法
右図での、左側のおもりの運動方程式は
- ma=Tーmg
である。 右図での、右側のおもりの運動方程式は、
- Ma=MgーT
である。
加速度aおよび張力Tを求めるには、この運動方程式の2式を連立して解けばよい。
- 答え
さまざまな力
[編集]摩擦力
[編集]
図の場合、押す力 f と静止摩擦力 F とは、つり合っている。また、重力 W と 垂直抗力 N とは、つり合っている。
摩擦力(まさつりょく、friction force)も、力の一種でありベクトルで表わされる。一般に、摩擦力には静止摩擦力と動摩擦力の2通りがあることが知られている。
静止摩擦力
[編集]静止している物体を動かし始めるのに必要な力を静止摩擦力(せいしまさつりょく、static friction force)という。
水平な机の上に置いた物を、水平方向に動かそうとして水平方向に引いてみても、加える力が小さいうちは、動かない。 同様に、机の上に置いた物を水平方向に押してみても、やはり加える力が小さい内は、動かない。
これは、摩擦力(まさつりょく)が、机の面と平行な方向の動きをさまたげようとして、加えた力とは反対向きに、摩擦力が働いていて、つり合っているからである。
物体を引いて動かそうとして力を加えているときは、引く向きとは逆向きに、摩擦力が働く。 同様に、物体を押して動かそうとしているときは、押す向きとは逆向きに、摩擦力が働く。
このように静止している物体に対して働く力を静止摩擦力(static friction force)という。 静止している物体を動かすには、摩擦のため、力が余計に必要になる。
加える力が大きくしていくと、そのうち、加えた力の大きさが、摩擦力をこえて、動き始める。つまり、ある物体の静止摩擦力には、大きさに上限がある。 物体が動き出す直前の摩擦力を最大摩擦力(さいだい まさつりょく、maximum functional force)という。静止摩擦力を F として、最大摩擦力を F0 とすれば、これらの関係を式で表わすと、
となる。
最大摩擦力 F0 の大きさは、物体と面とが、互いに垂直に押しあう力、つまり垂直抗力(すいちょく こうりょく) の大きさに比例する。垂直抗力の記号は N で書くのが普通である。 最大摩擦 F0 と垂直抗力 N の関係を式で書くと、
となる。
は比例係数であり、定数であり、静止摩擦係数(せいしまさつけいすう、coefficient of static friction)と言う。 静止摩擦係数は物質ごとに決まる定数であり、実験によると、物質と面のそれぞれの材質によって決まり、接触面積にはあまり関係しない。
摩擦係数は、例えばゴムでは非常に大きい。靴の滑り止めなどにゴム製の素材が使われる理由の一つは、このような理由である。また、スケートリンクの氷の上で物体を滑らせると、滑らせた物体が静止すること無くいつまでも滑り続けている様子が観察される。これは、氷は摩擦係数が小さいからである。
物体が載っている床に物体が沈まないためには、床が物体を押し返す必要があるので、このような床からの反発力を考える必要がある。 このような床から物体に掛かる力は、床からの抗力(こうりょく、reaction)と呼ばれる。床の面の接線方向に対して、抗力の方向が垂直なので、垂直抗力(すいちょく こうりょく)とよばれる。
摩擦角
[編集]
ある板に物体を乗せ、この板ごと傾けると、ある傾きをこえた段階で、物体が滑り始める。このときの角度を摩擦角(まさつかく、friction angle)という。この摩擦角の大きさ は、物体の重力 mg の、板と平行方向の分力 が、最大摩擦力 μN (=μmg cosθ )を越えたときの角度である。
なお、物体の質量を m とした。また、静止摩擦係数を とした。
なぜ、摩擦角の大きさがこうなるかというと、まず、物体は重力を受けて、鉛直下方向に mg の力を受ける。 このうち、この力は斜面方向に
であり、面に対して垂直な方向に
の大きさを持っている。このとき静止摩擦力の最大値は
となるので、斜面方向に働く重力 が、摩擦力 よりも大きいとき、この物体は動きだすことになる。 よって、このような の条件は、
よって
となる。
なお、「tan」とは三角関数のタンジェントであり、 で定義される。
このように、摩擦角の大きさは質量によらない。
動摩擦力
[編集]
あらい面の上を滑っている物体にも、摩擦力が掛かるので、外部から力を加えないでいると、やがて止まってしまう。このように、すべっている物体にかかる摩擦力を 動摩擦力(どうまさつりょく、kinetic friction force) と呼ぶ。
動摩擦力の大きさ は、垂直抗力(N)に比例する。
この係数 を 動摩擦係数(coefficient of kinetic friction) という。
は、おもに材質によって決まり、物体の滑る速度には、ほとんど依存しない。また、は、物体の接触面積には、ほとんど依存しない。
一般に、動摩擦係数の大きさは、静止摩擦係数よりも小さい。すなわち、
である。


あらい水平面上で、物体に糸をつけて、水平方向に引くする。引く力を大きくしていくと、引く力の大きさと、摩擦力の大きさの関係は、右の図のようになる。
- 参考: 転がり摩擦 (※ 計算問題にしづらいため、入試では出題されにくい)
先ほどの節で学んだ、面上を滑る場合の摩擦力は、滑り摩擦(すべり まさつ)という種類の摩擦である。 一方、小球が転がったり、円筒が転がったりする場合の摩擦を、転がり摩擦(ころがり まさつ)という。(転がり摩擦も、検定教科書の範囲)
-
ベアリング。玉軸受(たまじくうけ)。
-
玉軸受の断面
-
ベアリング。ころ軸受(ころじくうけ)。
転がり摩擦力は、滑り摩擦力よりも、小さい。車輪やベアリング(軸受け)は、この転がり摩擦の原理を利用したものである。「軸受け」は「じくうけ」と読む。
高校の理科や、大学入試の理科では、転がり摩擦については、あまり扱わないので、普通科高校の読者はあまり転がり摩擦に深入りしないこと。
機械部品に使われているベアリングの場合、物体間に潤滑油(じゅんかつゆ)や、粘性(ねんせい)の高い油性のグリスを加えてあり、滑りやすくしているのが普通である。(※ 普通科高校の理科では範囲外だろう。普通科の生徒は、この文を気にしなくて良いだろう。)
- 参考: ハイドロ プレーニング (※ 計算問題にしづらいため、入試では出題されにくい)


物体間に水や油などの液体があると、滑りやすくなる。雨の日の濡れた路面では、滑りやすくなる。人間も、雨の日の道路で滑りやすくなるが、自動車や自転車なども滑りやすくなる。 また、滑るため、ブレーキが効かなくなり、この現象をハイドロ プレーニングといい、とても危険である。
タイヤに溝があるのは、水を排出しやすくして、滑りにくくするためである。だが、それでも晴れの日の乾いた地面と比べれば、雨の日は滑りやすい。また、高速で走行すると排出が追い付かず、ハイドロプレーニングが起きやすくなる。なので、雨の日は、ゆっくり目に、車間距離を多めにして、安全に運転する必要がある。
- その他、自動車関連の摩擦の話題 (※ 計算問題にしづらいため、入試では出題されにくい)
市販の資料集を読むと、この他にも、自動車のブレーキと摩擦の関係、レーシングカーと垂直抗力の関係、自動車のABSの仕組みなど、いろいろな話題が書いてあったりする。(たとえば数研出版の資料集など) だが、始めて摩擦を習う諸君の場合、当面は、そこまで深入りしなくても良いだろう。実際に検定教科書や、多くの参考書でも、そこまでは説明されていないのが普通である。物理学的には、応用として興味深い話題だが、いかんせん読者の高校生には物理に使える学習時間が限られている。他の教科も勉強しなければならない。
液体や気体に関する力
[編集]圧力
[編集]
同じ重さの おもり でも、スポンジと接する部分の面積によって、めりこむ深さが違う。狭い面積で接するほど、その面積に重さの力が集中し、スポンジに深く、めりこむ。
圧力(あつりょく、pressure)とは、単位面積あたりに(たとえば 1m2 あたりに)垂直に押す力の大きさである。体の一部分を指で押した場合と、とがった針のようなもので押した場合とでは、同じ力で押したとしても結果に違いが出る。前者では皮膚がへこむ程度で済むが、後者では皮膚が破れてしまうこともある。これは、後者の方が皮膚に働く圧力が強いことによる。
圧力は単位面積当たりに働く力のことであり、働く面積が小さいときには単位面積当たりに働く力は強くなる。そのため、鋭くとがった針に力をかけたときには、皮膚に対して強い圧力がかかったのである。
圧力の単位はN/m2(ニュートン毎平方メートル)である。これは、力の単位を(たとえば N ニュートン)、面積の単位で(たとえば m2 で)割ったもので与えられる。このはN/m2の単位は、Pa(パスカル)と略される。「Pa」の 頭文字 P は、大文字で書くのが普通である。

大気中にある物質は、大気から圧力を受けている。この大気による圧力を大気圧(たいきあつ、atmospheric pressure)という。 大気にかぎらず、気体は、接する物質に圧力をおよぼす。気体による圧力を気圧(きあつ)という。
水中にある物質は、まわりの水から圧力を受けており、この水による圧力を水圧(すいあつ、fluid pressure)という。
この大気圧や水圧のように、液体や気体の中にある物質は、まわりにある液体または気体からの圧力を受ける。
液体や気体は、流れることができるので、液体と気体をまとめて流体(りゅうたい、fluid)ということもある。
- 備考
大気圧について、1.013×105Pa を、 1atmという。atmは「アトム」と読む。 また、ヘクトパスカル(hPa)を用いれば、 1.013×105Pa = 1013hPa である。
hは102を表す接頭辞(せっとうじ)である。
我々の住む地表は大気の海の海底にあると解釈することが出来て、我々自身も大気自身から強い圧力を受けている。このような圧力に耐えるため、我々の体は内側から大気圧とちょうど同じ程度の圧力になるように、大気圧を押し返している。このことによって大気圧に耐えることが出来ているのである。
このことはしかし、急激に回りの大気の圧力が下がったときに身体に変調をきたすことに通じてもいる。例としては、人間は生身で宇宙空間に出ることが出来ないことがあげられる。宇宙空間には酸素が無いことからヘルメットのようなものをつけて酸素を供給することが必要な事は確かである。しかし、宇宙空間のように極端に圧力が低いところでは、人間は、体に異常を感じると考えられる。そのため、全身を宇宙服でくまなく覆い身体の回りの圧力を地上での圧力と同じ程度に保つことが求められるのである。
水圧と浮力
[編集]水圧
[編集]
物体を水に沈めると、物体は水によって全体に圧力を受ける。このように水の中にある物体にかかる圧力を、水圧(fluid pressure)と呼ぶ。水圧は水の深さだけによって決まる性質があり、方向によらない。したがって、同じ深さでは、水圧の大きさは、どの方向でも同じである。また、水圧の大きさは、水の深さに比例する。
そして、水圧の力の大きさの値は、その上にある流体の重さによって決まる。その圧力の値は、流体の重さの作る力を、圧のかかる面積で割った値である。
水圧 p[Pa]の式は、つぎの式になる。
なお、水圧を与える液体の密度を [kg/m3] として、液体が存在する地点での重力加速度を とした。
なぜこうなるかというと、深さ h[m] での力をF[N]とすると、
(圧力の値は、流体の重さの作る力を、圧のかかる面積で割った値である。)
大気圧を考慮すると、大気圧をP0[Pa]とすれば、水圧p[Pa]は
である。
- 例
深海探査を行う船は、外壁に使う金属間の継ぎ目に大きな圧力がかかるため、その圧力に堪えられるだけの強度を持った細工をしないと、継ぎ目が砕けて船全体が水に浸かってしまう。
- 例
空気圧も空気の深さだけによっている。そのため、高い山に登ることによって空気圧が低くなった情况を見ることが出来る。空気圧が低くなったことの代表的な現象として、袋詰めになっている食糧などがふくらんでしまうことがあげられる。これは、回りの空気圧が下がったのに対して、袋詰めになっているものの中の圧力は変化することが出来ないので、相対的に袋の中の圧力が外の圧力より高くなったことによる。また、高山では湯を沸かしたとき沸騰の温度が 100 よりも低くなる現象も、空気圧が低くなっていることによる現象である。これは、物質の沸点がまわりの物質の圧力に依存していることによる。
浮力
[編集]
水に軽い物体を沈めると、その物体はどこからか力を受けて水から浮き上がって来る。この力を浮力(ふりょく)と言う。 浮力は、物体の鉛直方向の上下面が液体から受ける、上向きの力と、下向きの力との差によって生じている。
水に浮かぶ物体が静止するときは、物体の重さと、浮力とが、釣り合っているときである。

また、浮力の大きさは、水面から下で物体が排除した重さによる力の大きさに等しい。
液体中で静止している物体について、浮力の大きさの値は、水面から下にある物体体積が排除した重さによる力の大きさに等しい。これをアルキメデスの原理という。
よって、体積 V[m3] の物体にかかる、浮力 F[N] の大きさは
である。
- 証明
右図のような円柱状の物体が水中にあるとしよう。
そもそも、浮力の力は、物体の上下面の受ける、水圧による力(ちから)の差によるものである。 まず、水圧を求める必要があるので、上面および下面での水圧をそれぞれ求める。
大気圧を p0[Pa] とすれば、上面に掛かる水圧 p1[Pa]は、
下面に掛かる水圧 p2[Pa]は
である。
水圧により、上面に掛かる力 F1[N] は、
である。
水圧により、下面に掛かる水圧 F2[N] は
である。
F1 と F2 は逆向きであり、F2 のほうが深い場所(h2 = h + h1 ) にあるので F1 よりも大きい。つまり、F1 > F2 である。 なので、差し引き、 が、浮力として働く。 浮力を計算すると、
である。
よって、これまでの結果をまとめると、浮力 は
さて、体積 V は、
である。これを浮力の式に代入して、
よって、物体にかかる浮力は、物体の体積に比例する。また、浮力が、液体の密度にも比例する。
これらの比例関係を合わせると、物体が受ける浮力は、物体が押しのけた液体の質量に比例することになる。
このとき、立方体に水圧によってかかる力は、物体の上の面より下の面の方がより深い位置にあることから、物体には上向きの力が働くことが予想される。このため、物体には上向きの力が働きこの力がちょうど浮力に対応するものになるのである。また、今のことから浮力は、物体の高さに比例する。また、圧力に圧力を受ける面の面積をかけたものが力によって生じる力になるので、浮力自身は物体が圧力を受ける面の面積にも比例する。さらに、より正確には物体にかかる浮力は物体が沈められている液体の密度にも比例することが知られている。そのため、これらを合わせると、物体が受ける浮力は物体が押しのけた液体の質量に比例することが分かるのである。
パスカルの原理
[編集]
- (※ 未記述)




















































































