高等学校物理/物理I/運動とエネルギー
高等学校理科 物理I > 運動とエネルギー
本項は高等学校理科 物理Iの運動とエネルギーの解説である。
物体の運動
[編集]運動の法則
[編集]仕事とエネルギー
[編集]剛体に働く力の釣り合い
[編集]


力を加えても伸び縮みをせず、大きさを物体を剛体(ごうたい、rigid body)という。これに対して、バネなどの伸び縮みをする物体は弾性体(elastic body)という。 以下の記述では、おもに、剛体について考える。
剛体に力が掛かっている箇所を、作用点(さようてん、point of action)と言い、作用線から力の方向へ延長した直線を作用線(line of action)という。 剛体は力を加えた位置によって、動き方が異なる。力の加え方によって、並進運動の他に回転運動をする場合もある。 また、てこの原理を考えれば、同じ大きさの力を加えても、作用点の位置によって、剛体に与える影響は異なる。このことからてこの支点と作用点との距離Lと、力Fの垂直方向成分F sinθとの積を考えると好都合である。この積FL sinθを、力のモーメント(moment of force)と言う。あるいは単にモーメント(moment)という。
てこ以外の剛体に対しても、任意の点Oからの距離を考え、これを支点として、この点Oからの距離Lと力の垂直方向成分F sinθ都の積でモーメントを定義する。モーメントの単位は[N・m]である。 モーメントをMと表した場合、
- M=FL sinθ
である。 剛体に掛かる力が複数個、有る場合については、その力による回転方向が基準にした回転方向と逆の場合は、マイナス符号に取る。 力のモーメントが釣り合っている場合は、モーメントの合計がゼロになり、この場合は、剛体は回転しない。
- 偶力
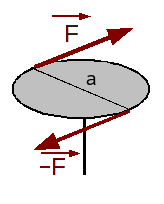

剛体に同じ大きさの力が反対方向に掛かっている場合、その力の対を、偶力(ぐうりょく、couple of force)という。
- 質点
剛体には大きさがあったが、この大きさを無視して、物体を質量を持った点として扱う場合は、これを質点という。 質点は、力のモーメントを持たない。
重心
[編集]
(Center of Gravity)
発展: 運動量と力積
[編集]
運動量
[編集]運動している物体Aが静止している物体Bに衝突して、その静止物体Bを動かしたとしよう。 このとき、静止している物体が動き出す速度の大きさは、物体Aの質量mAが大きいほど、衝突された物体Bの速度も大きな速度で動き出すだろう。また、物体Aの速度vAが大きいほど、衝突された物体Bの速度も大きくなるだろう。
このことから、速度vで運動している質量mの物体に関して、物体の速度vと質量mの積で定められる量mvを定義すると都合がよさそうである。
物体が動いているとき、物体の速度と質量の積mvを物体の運動量(うんどうりょう、momentum)と呼び、記号は一般にpで表し
と定義する。
運動量保存の法則
[編集]物体に対して力fをの間だけ 働かせたとき、
として、Pを力積(りきせき、impulse)と呼ぶ。 ここで、力積が運動量の変化率であることを示す。 実際ある物体に短い時間の間力
がかかったとすると、
となるが、これは運動量の時間変化率
に時間をかけたもので、運動量の時間変化に等しいことが分かる。 よって、物体にかかる力積は、物体の運動量の変化量に等しいことが分かった。
- 発展 微分と変化量
ここでは、短時間の運動量の変化率として、という記述を用いているが、本来この量はw:微分を用いて定義される。ただし、指導要領の都合のため、ここではそのような記述はしていない。微分を用いた導出については、古典力学を参照。
- 問題例
- 問題
静止していた物体に時間の間ある方向に一様な力fをかけた。物体が得た 運動量はどれだけか。更に、物体の質量をmとすると、物体がその方向に 得た速度はどれだけか。
- 解答
運動量の変化分は物体が受けた力積に等しいので、物体が受けた力積を計算すれば よい。物体が受けた力積は
に等しいので、物体が得た運動量も
に等しい。更に、運動量が
を満たすことを考えると、物体の速度は
となる。
運動量は、物体が全く力を受けないとき保存する。 これは物体に力が働かないときには、物体の受ける力積は0であり物体の運動量 変化も0であることから当然である。
さらに、複数の物体の運動量については、別の重要な性質が見られる。それは、 複数の物体のもつ運動量の総和はそれらの物体の間の衝突に際して 保存するということである。 これはつまり、例えばある2つの物体が衝突したとき、始めに2物体がそれぞれ持っていた 運動量の和は衝突が終わった後に2物体が持っている運動量の和に等しいということで ある。 ここで、いくつかの物体があるときそれらの持つ運動量の総和を、対応する物体系の 全運動量という。
物体の衝突について、運動量は常に保存する。しかし、物体系の全エネルギーは 常に保存するとは限らない。一般に物体の衝突についてエネルギーは常に失われていく。 もっとも物体系に限らない全エネルギーは常に一定であるので、物体が持っていた エネルギーは音や熱の形で物体系の外に逃げて行くのである。物体が衝突について 失うエネルギーは衝突に関わる物体が持っている物性定数によって決まる。 この係数をw:反発係数eと呼ぶ。反発係数は、物体が衝突したする前後の 物体間の相対速度の比によって定められる。 特に物体1と物体2が衝突前に速度 ,を持っており、衝突後に 速度,を持ったとすると、反発係数eは、
で定められる。ここで、右辺の始めの符合は、衝突の前後で物体の速度が より大きい物体は、衝突前により小さい速度を持っていた物体よりも 衝突後にはより小さい速度を持つことになるからである。 そのため、反発係数は一般に正の数である。 また反発係数は1より小さい数であり、物体間の相対速度は衝突前より 衝突後の方が小さくなる。特にe=1のときを完全弾性衝突と呼び のときを非弾性衝突と呼ぶ。完全弾性衝突のときは、 エネルギーは失われないことが知られている。一方、非弾性衝突の ときは物体系の全エネルギーは失われる。
- 問題例
- 問題
ある静止している物体2に運動量pで運動している物体が衝突した。このとき、 衝突した後の物体2が運動量を得たとすると、衝突後の物体1の運動量は どれだけとなったか。
- 解答
運動量の保存則を考えると、衝突の前後で物体1と物体2で構成される物体系の 全運動量は保存する。ここで、衝突前の物体系の全運動量はpであるので、 衝突後の物体系の全運動量もpとなる。更に、物体2の衝突後の運動量が なので、物体1の運動量は
となる。
ここで、物体系の全運動量が保存されることは、運動に関するw:作用反作用の法則から従う。 作用反作用の法則を用いると、物体系の間の衝突に際して、衝突に関わる それぞれの物体が受ける力は、大きさが等しく向きは反対となる。 このとき、それぞれの力に対して、衝突の時間をかけたものは 衝突に際してそれぞれの物体が受け取る力積に等しい。ここで、 衝突に関して働く力の力積を全ての物体について足し合わせると、それらの 和は上のことから0となる。しかし、全運動量の計算ではまさにそのような 全物体についての運動量の総和を計算しているので、衝突によって得られるような 力積の総和は0に等しい。よって、衝突に際して物体系の持つ全運動量は保存される。
- 問題例
- 問題
質量mの2つの物体が速度, で移動している。これらの物体が衝突したとき、 衝突後のそれぞれの物体の速度を、エネルギー保存則と運動量保存則を用いて 計算せよ。ただし、物体の衝突に関してエネルギーは保存するとする。
- 解答
この問題は2つの同じ大きさの物体を異なった速度でぶつけたとき その結果がどうなるかを計算する問題である。 実験の結果によると、一方が静止しており一方が動いているとき、 動いていた物体は静止し、静止していた物体は動いていた物体が持っていた 速度と同じ速度で動きだすことが知られている。ここでは、それらの 結果が計算によって確かめられることを見ることが出来る。 衝突後の物体の速度をそれぞれ物体1については,物体2については とする。このとき、物体の衝突について全エネルギーが保存されることを 用いると、
が得られる。更に、物体の衝突について物体系の全運動量が保存されることを用いると、
これらは、,についての2次方程式であり、解くことが出来る。 実際計算すると、解として
が得られる。前者の解は衝突に際して物体の速度が変化しないことを 示しているが、これは実際の情况として考え難いので、後者の解が現実の解となる。 この結果を見ると、物体が持つ速度が入れ替わることが分かる。
このことは実際に同じ大きさの球を用いて実験を行うと、確かめることができる。
日常に起こる物体の運動
[編集]現実の物体の運動においては、ただ1つの力だけで表わされるような運動は数少なく、いくつかの物体から受ける力がからみ合って物体の運動のようすが決まっていることが多い。
例えば、空気中に存在する物体に力をかけて運動させることを考えてみる。ここでは、物体はそれに力をかけている人間や道具から力を受ける。しかし、一方で物体は空気と衝突することで空気の分子から力を受けることになる。このため、一般に空気中で物体が行なう運動は、力をかけている人間が意図したものとずれる傾向がある。実際にこのような対応する力によって物体の運動の様子が大きく影響を受けるかどうかは、扱う現象の様子によって大きく変わってくる。分銅程度の大きさの物体を用いた短時間の測定なら、空気抵抗の影響は無視しても差し支えないと思われる。しかし、例えばロケットが大気圏に突入するときのロケットの運動は、空気抵抗によって大きく影響され空気抵抗の影響を無視して運動の様子を解析することは適切ではない。
このように、対象とする物体の運動の様子に伴って、どの力が重要になるかを正しく見抜くことが必要となる。
運動とエネルギーに関する探求活動
[編集]??



























