IS-LM分析
- マクロ経済学初中級 > IS-LM分析
はじめに
[編集]IS-LM分析とは
[編集]IS-LM分析とは、その名のとおりIS曲線とLM曲線を用いてマクロ経済を分析することである。イギリスの経済学者J.R.ヒックスがケインズの所得決定理論をグラフでみられるようにしたもので、ケインズモデルを端的に表現するグラフとされている。
具体的には、財政政策や金融政策に本当に効果があるのか? どれくらいの効果があるのか? また実際には財政政策・金融政策に効果がない場合があるが、それはなぜなのか? このような問題を論じる際にIS-LM分析は使われる。
IS曲線
[編集]IS-LM分析ではIS曲線とLM曲線を使ってマクロ経済の分析をする。IS曲線のISとはInvestment(投資)とSaving(貯蓄)の頭文字で、IS曲線とは投資と貯蓄が等しくなるような所得と利子率の組み合わせである。「#IS-LM分析とは」のグラフでいうと、IS曲線は右下がりの曲線である。
IS曲線において、なぜ投資と貯蓄が等しくならなくてはいけないかというとI(投資) = S(貯蓄) が財市場の均衡条件だからである。この均衡条件(I=S)が満たされていると財市場は均衡する。つまり、IS曲線は財市場の均衡を満たす所得と利子率の組み合わせであると言うこともできる。
IS曲線は右下がりであると先に述べた。ではなぜIS曲線は右下がりなのか?IS曲線は縦軸に利子率、横軸にGDPをとったグラフに書かれる(右下がりの)曲線である。このとき、IS曲線はGDPが利子率の減少関数となっていることを示している。そのためIS曲線は右下がりなのであるが、ではなぜGDPが利子率の減少関数となるのだろうか?
まず利子率が低い場合を考えてみよう。利子率が低いときは投資が多くなる。このとき、投資と貯蓄が等しくなる(財市場の均衡条件を満たす)ためには貯蓄も同じだけ増える必要がある。このとき、貯蓄が増えるためには所得(GDP)も増える必要がある。
そのため、IS曲線において、(財市場を均衡させるという条件の下では)利子率が低いときには所得(GDP)が高くなる必要がある。(財市場を均衡させるという条件の下では)利子率が高いときには所得(GDP)が低くなる必要がある。これは所得(GDP)が利子率の減少関数となっているということであり、これをグラフにすると右下がりの曲線となる。
IS曲線の導出
[編集]所得均衡式、消費関数、投資関数が次のように与えられたとする。
- (所得均衡式)
- (消費関数)
- (投資関数)
(Y:国民所得(GDP)、 C:消費、 I:投資、 G:政府支出、 NX:貿易・サービス収支(純輸出)、 r:利子率、 T:租税。)
このとき、消費関数と投資関数を所得均衡式に代入するとIS曲線が得られる。
これがIS曲線式である。 または
とも表せる。
練習問題
[編集]ある経済は次のモデルで描写される。ここでY:GDP C:消費 I:投資 G:政府支出とする。外国貿易はないものとする。
- 所得均衡式:
- 消費関数:
- 投資関数:
- 政府支出:
このとき、IS曲線を求めよ。
ヒント:C I Gを所得均衡式に代入するとIS曲線が得られる
LM曲線
[編集]LM曲線のLMとはLiquidity preference(貨幣需要)とMoney supply(貨幣供給)の頭文字であり、LM曲線とは貨幣需要と貨幣供給が等しくなるような所得と利子率の組み合わせである。「#IS-LM分析とは」のグラフでいうと、LM曲線は右上がりの曲線である。
LM曲線において、なぜ貨幣需要と貨幣供給が等しくなくてはいけないのだろうか? それは貨幣需要=貨幣供給が貨幣市場が均衡するための条件であるからである。貨幣需要 = 貨幣供給 が成り立っているときに貨幣市場が均衡するので、LM曲線は貨幣市場を均衡させるような所得と利子率の組み合わせと言うこともできる。
LM曲線は右上がりであると述べた。では、なぜLM曲線は右上がりなのだろうか?利子率が高い場合、貨幣需要は少なくなる。また、所得が多い場合、貨幣需要は多くなる。貨幣供給は外生変数なので、このとき貨幣供給を一定とすると、貨幣需要と貨幣供給が一致するためには「低い利子率と低い所得」または「高い利子率と高い所得」の組み合わせが必要になるのである。これをグラフにすると右上がりの曲線となる。
LM曲線の導出
[編集]LM曲線は貨幣市場の均衡条件から導出される。
M:名目マネーサプライ(名目貨幣供給量)L:貨幣需要 P:物価水準 Y:国民所得(GDP) r:利子率
ここで、MとPは外生変数。
このときは名目マネーサプライを物価水準で割ったもので、これは実質マネーサプライ(実質貨幣供給量)を示している。またL(Y,r)はL(貨幣需要)は変数Yとrによって決定される関数であるということを示している。
練習問題
[編集]ある経済は次のモデルで描写される。このとき Y:GDP r:利子率 P:物価水準 M:名目マネーサプライ とする。
次の条件、
- 貨幣需要関数:
- 実質マネーサプライ:
であるとして、このとき、LM曲線を求めよ。
ヒント:貨幣需要=貨幣供給が貨幣市場が均衡する条件なので、M/P=Lを解けばLM曲線を出すことができる。M/P=600で、L=Y+(200-10r)だから…
均衡国民所得と均衡利子率の決定
[編集]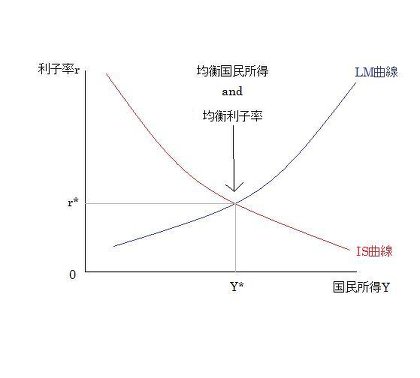
均衡国民所得はIS曲線とLM曲線が交わるところで決定される。このIS曲線とLM曲線が交わった点は均衡点と呼ばれる。よって、均衡国民所得はIS曲線とLM曲線の均衡点によって決定される、と言いかえることもできる。上の図で言うと、IS曲線とLM曲線の交わっている点が均衡点、均衡点のときの国民所得Y*が均衡国民所得であり、均衡点のときの利子率r*が均衡利子率である。
均衡国民所得と均衡利子率の導出
[編集]IS曲線の節で、ある経済でのIS曲線を算出する練習問題を出題した。この練習問題の答えとなるIS曲線は、
- ・・・①
である。 LM曲線の節でも、同様にLM曲線を算出する練習問題を出題した。この練習問題の答えとなるLM曲線は
- ・・・②
である。
IS曲線とLM曲線が交わる点で均衡国民所得と均衡利子率が決まるのだから、①と②を連立して解くことで、均衡国民所得・均衡利子率を導出することができる。つまり、
このrを②に代入して
よって、均衡利子率は14.17%、均衡国民所得は541.7ということになる。






















