中学校技術/プログラムによる計測・制御

プログラム

コンピュータの処理の手順をプログラムという。 プログラムを記述するための言語をプログラミング言語という。

順次、分岐、反復

フローチャート、順次の例

フローチャート、分岐の例

フローチャート、条件繰り返し（反復）の例

コンピュータは、特に指示がない限りは、前から順番通りに実行する。これを順次という。

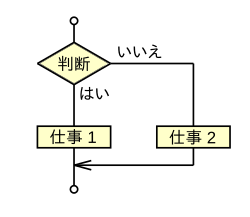
コンピュータは、条件によって（あるいは条件によらず）実行する順序を変えることができる。これを分岐という。

コンピュータは、同じ処理を繰り返すこともできる。これを反復という。

簡易なフローチャート これはsに1から10までの数字を足しこむ処理を表した図である。

Nの階乗 N! を計算するフローチャート

分岐と反復を組み合わせて、条件が満たされている間だけ処理を反復するような手順も、プログラムで指示できる。

プログラミング言語には様々な種類があるが、多くのプログラミング言語は、分岐や反復や順次処理などを利用している。

フローチャート

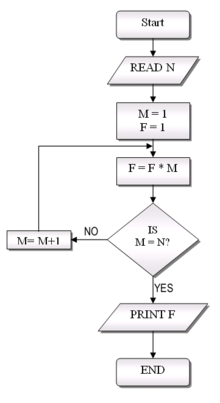
プログラムでの、順次や分岐や反復の組み合わせ方を、人間が理解しやすいように図示したものとしてフローチャートが有る。 横長のひし形(図では◇の横長のもの)で、条件分岐を表し、ひし形の中に、条件の内容を記述している。

順次処理は、横長の長方形で書かれる。処理内容は、四角の中に書かれる。

順番は、原則として、プログラムの最初が、フローチャートの一番上にあり、一番下が、最後の処理である。

プログラミング言語

プログラミング言語には多くの種類があるが、1960年代ごろからある古典的な言語では、BASIC(ベーシック)とC言語（シーげんご）とFORTRAN（フォートラン）やCOBOL（コボル）がある。

BASICは初心者向けとして有名であった。

C言語は、コンピュータで処理しやすいように文法が厳密である。歴史的にはオペレーティングシステムのプログラムの記述のために開発されたため、OSの開発など、システムの深い部分の処理にも利用しやすい。

C言語はコンピュータ技術者にとっては有用だが、それ以外の職業の用途では無用な特徴も多く、そのため、ほかの業界に合わせて開発されたプログラミング言語がある。

アクチュエータへの応用

外界からの情報を信号として出力する装置をセンサという。 以下、コンピュータに取り付けられるセンサについて記述する。

センサとは別に、コンピュータなどからの信号に基づき外界の物体を動かす装置をアクチュエータという。

センサとアクチュエータをコンピュータに取り付ければ、センサで外界の状況を確認できるので、外界の状況が変わっても、センサで外界を確認しなおして、プログラムの判断基準（プログラムの条件分岐の機能を、アクチュエータの判断基準に応用できる。）に従い、アクチュエータで外界の物体をプログラム通りに動かせる。 このように、コンピュータ制御のアクチュエータを、センサと連動させることで、外界の環境変化に対応するアクチュエータを作ることができる。

一般に、パソコンの単体には、センサやアクチュエータは付属していないので、もしセンサやアクチュエータが必要な場合は、パソコン用のセンサやアクチュエータを購入などで入手してから、それらをパソコンに取り付けることになる。

（※ 範囲外: ）論理代数

※ 2019年現在の中学技術の検定教科書では、下記のような条件判定については習わない。

ただし、資料集などで紹介される可能性があるので、wikibooksに残しておく。

コンピュータの分岐機能での条件判定では、次のような判定が出来ます。

条件	数学の記号
AとBは等しい	$A=B$
AはBより大きい	$A>B$
AはBより小さい	$A<B$
AはB以上	$A\geqq B$
AはB以下	$A\leqq B$
AとBは等しくない	$A\neq B$

センサーなどを用いてアクチュエータ制御の条件判定を行う場合は、センサーの信号を数値に置き換えて行います。

また、複数の条件判定を組み合わせた条件判定もあります。次に示す、論理積や論理和などです。

• 論理積

AND回路の説明図。この図は X and Y の図である。
電球がつくのは、スイッチXとスイッチYの両方が閉まっている時だけである。（スイッチが閉まっている状態を1とする。スイッチが開いている状態を0とする。）

たとえば、条件Xと条件Yの両方が満たされている時にのみ、ある行動を実行する条件判定をAND（アンド）という。このANDとは英語の接続詞の 「and」 のことである。式では、

X and Y

などと書く。

仮に条件が満たされていない場合を数字の0として、条件が満たされている場合を1とすると、andの性質が、掛け算に似ているので、そのことからAND演算を論理積（ろんりせき）ともいう。 ある条件Xが満たされていることを真（しん）と言う。ある条件が満たされていない場合を偽（ぎ）と言う。 条件が真の時、これを数値の1で表すことができる。条件が偽のとき、数値の0で表すことができる。なお、このように、条件の数値を数値の1と0に置き換えて計算する代数学をブール代数（ブールだいすう）という。

論理積の真理値表

条件 P	条件 Q	P and Q
真	真	真
真	偽	偽
偽	真	偽
偽	偽	偽

• 論理和

条件Xと条件Yの少なくとも、どちらか片方が満たされている時に、ある行動を実行する条件判定をOR（オア）という。このORとは英語の接続詞の 「or」 のことである。式では、

X or Y

などと書く。OR演算のことを論理和（ろんりわ）ともいう。

命題 P	命題 Q	P or Q
真	真	真
真	偽	真
偽	真	真
偽	偽	偽

• 否定

他にも、条件Xが満たされていない場合に、（その他の条件Yなどについては不問）、ある行動を実行する条件判定をNOT（ノット）と言う。式では、

not X

などと書く。NOT演算のことを否定（ひてい）と言う。

命題 P	notP
真	偽
偽	真

• 排他的論理和

他にも、条件Xと条件Yの少なくとも、どちらか片方のみが満たされている時に、ある行動を実行する条件判定をXOR（エクスクルーシブ/オア）という。式では、

X xor Y

などと書く。XOR演算のことを、排他的論理和（はいたてき ろんりわ）とも言う。

条件判定のANDやORなどを回路図の一部として図示したものとして、論理回路がある。条件が満たされた時を、回路に電流が流せる時と同一している。 たとえば、AND回路では、A and B なら、Aに対応するスイッチとBに対応するスイッチが閉じることで、回路に電流が流せるようになる。 NOT回路では、not Aなら、普段はスイッチが閉じていて、条件Aが満たされた時に対応するスイッチAが開き、電流が流せなくなる。

• 

  AND回路
  A and B

• 

  OR回路
  A or B

• 

  XOR回路
  A xor B

コンピュータのハードウェア内部では、半導体素子の一種であるトランジスタのスイッチング機能を用いて、論理回路を実現している。このようなハードウェアの仕組みを利用して、コンピュータは論理演算を行っている。なおトランジスタが実用化される前には、パラメトロンや三極真空管を、更に真空管が実用化される前には、継電器（リレー）を用いて、スイッチング機能を実現していた。

（トランジスタのスイッチング機能については工業高校や工学系大学の教育内容になる。）

中学の段階では、トランジスタの仕組みについて、まだ知らなくても良い。

補足

プログラミング言語の具体的な文法については、ウィキブックス内には、記事プログラミングなどに解説があります。 実習などで用いる言語は、時代によって変わるかもしれません。また、実習の内容によっても変わります。 たとえばウェブページを作る場合のプログラムはHTML（エイチ・ティー。エム・エル）という言語で記述を行う場合が多いです。

また、学校で用意された実習キットなどを用いてプログラミングを行う場合は、そのキット用に開発された独自の教育用のプログラミング言語を用いる場合もあります。

中学の段階なら、BASICか、その派生言語を使うことが、あるかもしれません。

デバッグ

※ 令和3年度から、デバッグの話題がこの単元に加わります。（東京書籍などのwebサイトの技術科教材のカタログPDFで確認。）

プログラミングでは、とりあえず一応のプログラムを書けたら、今度はそのプログラムを実験的に動作させてみて、本当に安全かつ正常に動くかどうかを確認する必要があります。

人間の入力ミスや、勘違いなどによって、プログラムが異常な動作をしてしまう場合もあります。

なんらかの原因で、プログラムが異常な動作をすることを「バグ」と言います。

プログラムにもしもバグがあったら、つまり、なにか異常な動作、正常でない動作をするなら、これは修正しないといけません。このように、バグを取り除いて、プログラムを正常に直すことをデバッグ(debug)といいます。

前提として、プログラムを作った後は、まず開発企業などが自分たちで、本当にそのプログラムが正常かどうかを実際にプログラムを動作させる実験によって試す必要があります（この工程を「テスト」と言います。）。もちろん、時間の制限などもあって、完全には確認しきれませんが、なるべく時間の許すかぎり、プログラムを確認する必要があります。

また、プログラムのエラーだけを除くのではなく、たとえば画面のあるシステムを作っている場合なら、画面が第三者の利用者にも見やすいかのチェックや、操作が分かりやすいかなどもチェックもデバッグにおいて確認する場合もあります（※ 開隆堂の検定教科書）。

（※ たぶん範囲外: ）説明の都合上、プログラムを例にして説明していますが、コンピュータ業界以外の製品開発なども同様に、安全性などを実際に動作させることでテストする必要があります。

自動車会社なら実際に走行試験や衝突実験（エアバッグの動作などの確認）をしています。製薬会社では、実際にネズミやイヌなどの動物を使って実験をしたり（動物実験）、最終段階には人間を希望者をあつめて新薬の実験の被験者になってもらいます（人間を被験者にした新薬の実験のことを「治験」（ちけん）と言います）。

なお、テストのために動作確認をする前提として、まず、その製品の正常な動作を、決める必要があります。（これをIT業界で「仕様」(しよう)などと言います。）

「〇〇の条件のときに、このプログラムは△△の動作をする」という仕様でしたら、果たして本当にプログラムがそのとおりに動作をできているか、実験をして確認をします。

「検証」の要求水準

※ たとえば、東京書籍の教科書の例ですが（※ 教科書では断言はしてないが）、「温度が25℃以上に高くなったら、扇風機を回す」というプログラムならば、実際に室温などの温度を25℃以上に上昇させる実験をする必要もあります。そして、その温度（25℃以上）になったら、本当に扇風機が回ってるかどうかを確認します。 けっして、「実際の物理実験ではなく、情報技術を駆使して、25℃以上のデータ入力信号をプログラムに送ってみる」みたいな信号処理だけで済ますのではなく、最終的には実際に室温を25℃以上にします。そこまで実験するのが、製造業では当然です。（※ 教科書では断言してないが、しかし製造業では、最低限でも このくらい以上の確認をするのが常識。） 製造業でも、コンピュータなどで強度計算シミュレーションなどをする事もありますが、最終段階では、自動車会社なら衝突実験などの物理的な実験で、どの程度で壊れるか/壊れないかなどを物理的な実験で検証します。また、自動車会社での流体解析でも、試作の初期の段階ではコンピュータを援用することもありますが、さらに風洞実験（ふうどうじっけん）などで確認し、さらに最終的には走行試験などでも検証します。 コンピュータや理論家が、どんなに立派な数式を用いてシミュレーションしていても、それはその予想が正しいことの証明になりません。 （歴史でも、数学の方程式をもちいた理論にもとづく予想が外れたこともある（高校レベルなら「タコマ橋の崩壊」など。大学レベルなら、流体力学のナヴィエ・ストークス方程式で有名な土木工学者ナヴィエの設計した橋もあっけなく崩壊した。）。 中学校・高校では、当たった予想だけを習うので、ついつい勘違い（「数式にもとづく予想は絶対に正しい」（×）という勘違い）しがちになるが、しかし現実はそうではない。） 工業などにおける、シミュレーションや理論・数式の正しさの検証は、最終的には、じっさいに物理的な実験によって確認が行われなければなりません。（※ 日本のJAXA（航空宇宙関係の国立研究所）や産総研（産業技術総合研究所）なども、そういう見解です。JAXAのそういう見解については、たしか書籍の 講談社ブルーバックス『小惑星探査機「はやぶさ」の超技術』で確認できたと思います。産総研のほうは、出典はあるのですが、教科書では事情で出せません。） たとえば2011年（東北大地震）の原発事故のあとの国の研究所の対応でも、そうです。災害復旧ロボットなどの試験では、国の試験場（実験試験のための広いこ国有地がある）などにガレキの山を用意して、そういう不整地な足場のわるい場所であっても実際にうまくロボットが動作して目的の活動をできるかもテストしたという実例もあります。 論文が多いかどうかとか、そういうのは無関係です。 外国の例でも、アメリカ合衆国のNASAや米軍研究所（DARPAなど）でも同様、最終的には、物理的な実験で確認します。（日経サイエンスの増刊号『ロボット・イノベーション』に、ここら辺の話題が書いてある。なお日経サイエンスはじつはアメリカの科学雑誌『サイエンティフック・アメリカン』の日本語版。米国のロボット試験場には、ガレキなどの山があったり暴風雨（大量のシャワー放水 と 多数の大型扇風機（工業用） などで暴風雨を再現したりする）のようなテスト環境も用意されており、こういった過酷環境を再現したロボット試験場のことを英語で「ディスアスター・フィールド」(disaster field  ? （※ 翻訳がネットで見つからず）)と言います。米国の軍用ロボットなどは、この過酷なディズアスター・フィールドで実験的に試験されています。） ※ 福島ロボット・テストフィールドというのが今度の令和3年度教科書で紹介されるらしいですが、ロボットのテストのフィールドというのは、分野によってはこういうレベルである。 中学校なら、設備などの制約もあるので、そこまで本格的には実験する必要は無いです。しかし、せめて最低限でも、25℃の扇風機プログラムの検証なら、ためしにエアコンでも使って実際に室温を25℃以上にしてみるぐらいの確認実験はするのが望ましいでしょう。 きびしめの事を書きましたが、大学生でも、ここまで考えられてるかどうかアヤシイので、あまり深刻にならず、頭の片隅にでも入れておきましょう。 なお、芸術系の大学などであっても、美大生などが家具とかをデザインする際、教授がその家具を普通の使い方をしてみて（強度不足などの理由で）壊れたら、その科目の学生の成績評価は『不合格』とするという言い伝えもあるくらいです。

※ なお、温度を電流に変換するための電子素子としては、PTCサーミスタという素子があります（※ ネットの教科書画像でPTCサーミスタの紹介を確認。教育図書の教科書とのこと）。

フェイル・セーフ

バグを見つけて除くデバッグも重要ですが、万が一、バグを見過ごしてしまった場合でも、人が死ぬことや怪我などの取り返しのつかない大被害が出ないように設計することも必要です。

そのように、もしバグや故障などの誤動作などがあっても、システムが安全に稼働するように設計することをフェールセーフ（fail-safe）またはフェールプルーフ（fail-proof）と言います（※ 2022年代の中学技術の検定教科書にフェールセーフが書いてあるらしい）。

「フェイル」fail とは、「失敗する」・「失敗」などの意味の英語です。

たとえば、機械工場で生産システムを管理しているコンピュータの場合、もしシステムが異常を感知したら、そもそも通常起動をしないようにするべきです。

なぜなら、異常のある状態で高圧プレスなどを制御されたら、もしかしたら事故で作業員が死ぬ可能性があります。

かといって、すでに稼働している最中でシステムが級に故障した場合に、果たして急停止するべきかといわれたら、それは場合によっては疑問です。

もしシステムが急停止したことで、逆に人がケガをする事故が起きては困ります。

なので、システム稼働中の事故に対しては、たとえば徐々に減速していく、とかの設計になるでしょうか（職場や製品やシステムによって、適切な設計は変わります）。

ともかく、システムの異常時には、事故防止のため、安全にするための処理が自動的に起動して動作するような感じの設計、または、安全だと認められる処理以外の手作業での入力をシステムが受け付けないように設計するなど、安全措置（あんぜん そち）以外をできないようにする必要があります。

このように、安全側にシステムのモードを移行するための仕組みを組み込むような設計のことが、フェイル・セーフまたはフェイル・プルーフと言われるものです。

なお、仮にプログラムにバグが無くても、部品の故障によってエラーが起きる場合もあります。なので、工場などで使うプログラムでは、フェイル・セーフも必要です。

設計技法の初歩

さて、ある検定教科書では、サーバ・クライアント通信のプログラムを、アクティビティ図を用いて設計する手法を紹介しています。

果たして中学でそこまで必要になるかは不明ですし、そもそも中学レベルの技術力でそういう通信プログラムが書けるのか不明ですが、しかしとりあえず、（※教科書では説明していませんが、）一般的なプログラミングにおける設計技法として、自分の作ろうとしているモノが何なのかを、箇条書き（かじょうがき）などで紙にまとめる必要はあります。

なぜなら、検定教科書では説明されていませんが、

プログラミングは集中力を使うので、いちいち「何を作ろうかな」と考えながらプログラミング作業するのは難しいからです（※ 検定教科書では説明していませんが）.

また、会社や組織などの集団でプログラム製作をする場合は、個々人でイメージしている目標や指示などに食い違いが出ないように、目標などを文書で具体化する必要もあります。

要件定義

仕事などだと、上司や部下・同僚など他人が読んでもわかるように設計書を書く必要があります。（おそらく、検定教科書が意識してるのはコッチ。）

設計書では、大まかな要件を先に決定していき（ただし、比較的に短期間かつ自力たちで実現できる具体的な目標）、それを元に段階的に、追加の文書により細部を決めていきます。

どちらにせよ、まず、設計目標が何なのかを明確に文書に起こす必要があります。別に文体が美文である必要はありません。

そして、その目標に必要な最低限の技術的に実装すべき対象が何なのかを明確にしていきます。

※ 検定教科書にはない用語ですが、こういった作業を「要件定義」（ようけん ていぎ）などと言います。アクティビティ図などを紹介するその検定教科書が説明しようとしているのは、おそらく要件定義の方法でしょう。

※ ただし、中学生では、そもそもプログラミングでどんなことが出来て、何が出来ないかも知らないので、要件定義をするのは難しいかもしれません。だから、とりあえず知識として、仕事などでは要件定義のような手法が必要になる場合も多い、ということを知っていただければ十分かもしれません。

（※ 範囲外: ）やることリスト

プログラマーとしては事前にメモ書きのようなものでいいので、紙またはテキストファイルなどに、作りたいプログラムの満たすべき要件をまとめておくなどしておくと、いちいち目標を定期的に思い出す手間が省け、思考力を節約できるので、プログラミングに集中しやすくなります。（検定教科書では紹介されない用語ですが、こういうのを「To doリスト」とか「作業リスト」とか「タスクリスト」とか「やることリスト」などといいます。）

※ ただし、検定教科書の論点は、どちらかというと自分の思考の整理よりも、他人に設計を伝えるための手法としてアクティビティ図などを紹介していますが。だから「先生や友達」が読んでもわかるように書こう、などと検定教科書で説明しています。

ともかく、プログラミングの入力の前に、まず「自分たちは何を設計したいのか」を具体的に紙または画像データに書き起こすことです。検定教科書ではフローチャートの書き方などを教えていますが、それはあくまで、入力したいものを明確にする手段のひとつです。

そうやって具体的に見て分かるように文章化または印刷化・画像化をしておけば、打ち合わせをするにしても、あるいは忘れないようにするためにメモ代わりにするにしても、どちらにも役立ちます。

要は、「何を入力したいのか？」を読みやすい形式でメモ的に書いておけばいいのです。

プログラミング的な知識

ソート

並び順を変えることを「ソート」と言います。

ソートには、選択ソートや交換ソートがあります（※開隆堂のサイトで確認）。開隆堂サイトでは、トランプ（カードゲームのほう。カード４枚）の並び替えをしていました。

ゲームの「仕様書」

※ 出版社は未確認だが、ゲーム版のラブライブのゲーム（スマホゲー）を例に検定教科書で仕様書の書き方を説明している教科書があるとのこと。

ゲーム業界の例なのですが、ゲーム業界では「仕様書」（しようしょ）として、ある画面の動作の条件をすべて具体的に書きます。

また、基本的に具体的な画面を使って動作説明すことで、客観的に誰でも分かるように説明しています。

※ ゲーム産業だけでなく一般のIT産業の多くでも似たような書類での説明方法が用いられる。なので教科書では

たとえば、ある画面では、

• 「Backボタン」→「呼び出し元の画面へ遷移する」、　

• 「部員のイラスト」→「クリックしても何も起こらない」

• 「変更ボタン」→「自分のプロフィールの場合」→「クリックすると自己紹介ポップアップを表示する」

（「変更ボタン」）→「他ユーザーのプロフィールの場合」→「変更ボタンを表示しない」

のように具体的に書きます。（※　なお、製図などとは違い、仕様書では日本共通の書き方というのは存在しません。仕様書の規格も存在しません（2023年の時点ではそう）。）

（※ wiki注）上記の仕様の「呼び出し元の画面へ遷移する」などの文章は教科書画像からの引用。なので、決して上記文章の言い回しを変えないでください。

前の画面に戻るためのボタンのように、文脈から分かることでも、上記のように具体的に書きます。

イラストのように、クリックしても何も起こらない場合ですら、何も起こらないことを仕様書では明記します。そうすることで、その仕様書のそのページさえ読めば、これからプログラミングで作るべき動作のゴール地点が分かるようにします。

もちろん、変更ボタンのように、クリックすると変更が起きる場合は、

「自分のプロフィールの場合」→「クリックすると自己紹介ポップアップを表示する」

のように何をどう表示するかも具体的に書きます。

このように、ソフトウェアの設計（デザイン）というのは、先にゴール地点を具体的かつ客観的に決めて、あとから細部をデザインしていきます。一般にゲームも同様、ゴール設定を先に行い、あとから細部を決めていきます。アイデアは、「なんのために」というゴールを達成するための手段です。

ゲームデザインではない単元ですが、教育図書（教科書会社）の検定教科書でも木工などの単元で、目的や条件から逆に（設計の）構想を考えるように指導しています。なお、実用品などの場合は、問題を先に見つけ、その問題を解決するために上記の目的や条件を考えます（※ 教育図書の見解）。

また、設計のための書類で使われれる文章のレベルも、中学卒業したレベルの知識さえあれば、とりあえず内容は分かるような文章で書く必要があります。

※ なお、同じコラムで、フローチャートの代わりにUMlを教えてる。ラブライブのゲームの仕様設計では、UMLを使っているらしい。

※ 範囲外

ロボット教材など

（※暗記は不要）ロボチャートなど

※ 実習などで習う範囲です。 フローチャート形式で表示されるファイルを編集することでロボットのプログラミングを行える、「ロボチャート」（スズキ教育ソフトの製品）というロボット・プログラミング言語がありますプログラミング入門ソフト〈ロボチャート〉 - スズキ教育ソフト 現代日本の中学技術の教育でも、こういった会社のソフトウェアがすでに実習などで使われています。 なぜ紹介したかというと、じつは教育だけでなく、製造業などの工場でも似たような発想の、Ｃ言語などが分からなくてもフローチャートなどさえ分かればプログラミングできるようなソフトウェアが存在しており、よく製造業などで使われます。 C言語など一般のプログラミング言語だと、機能が高度すぎるので学習に年月が掛かり過ぎてしまうので、土木技術者や機械技術者など非・情報系の技術者にはプログラミング言語として不適切なのです。 そこで、ロボチャート的な、C言語を使わなくてもフローチャートなどの画像のある編集ソフトでプログラミングできるソフトウェアが、じつは大手の電子機械（メカトロニクス）系などの会社などでは使われています。 （※　範囲外:）ロボチャートのほかの会社にも、そういった発想の制御系のプログラミング用ソフトは多々あります。 外資製品で有名なのだと、米国ナショナルインスツルメンツ社の「ラボビュー」というソフトが測定機器の業界でよく使われており、これもフローチャート的な画面を編集することでデジタル・センサーの入力データの処理をプログラミングするソフトウェアです。 このラボビューは、ロボット制御の業界でも使われています。なぜなら、ロボットにはセンサーが大量に必要なので、なのでラボビューによる測定機器の制御によってロボット制御も実行できるのです。 （※　範囲外:）Windowsを作っているマイクロソフト社が、こういった測定機器の制御ツールのための簡易的なプログラミング言語を2010年代に作っていました。上記のようなロボット制御と簡易的なプログラミングの関係の話を聞けば、マイクロソフトの意図は想像がつくでしょう。 なお、マイクロソフト社は、日本の自動車会社など大手製造業とも業務提携しています。 経済は分業で成り立つので、専門分野をもつのは好ましいですが、しかし決して専門だけにとらわれて異分野をまったく勉強しないなんてことは、しないようにしましょう。（つまり、少しは異分野も勉強しましょう。） 上記のように、製造業とソフトウェア産業は、意外なところで提携していたりします。消費者からは目に見えづらいところで、業務提携している大企業はあります。 ほか、日本の学校などでよく使われるロボットプログラミング教材のひとつとして、 レゴ　マインドストームがあります。おもちゃのレゴブロックを作ってる欧米の会社のです。当然、このマインドストームにも、センサーやモータなどが組み込まれたブロックがあります。 なお、こういったロボット教材に使うCPUは、パソコン用のものとは違います。 本wiki調査にて、小中高ロボット教材で使われていることが確認されている CPU としては arduino （アルディーノ） や ARM（アーム） などがあります。ARMは、携帯電話などにも使われるCPUです。 ほか、CPU形式ではなく、教育用のマイコン基盤としてボードに組み込まれた形式で販売されている場合もあり、 micro：bit や、Rasberry Pi （ラズベリーパイ）があります。日本企業のロボット教育用のマイコン基盤としては IchigoJam（イチゴ ジャム）もあります。 なお、micro：bit および Raspberry PiのCPUはARMです。 ほか、Arduino Uno というマイコンボードもあり、CPUはその名の通り Arduino であり、これも日本の学校での使用実績があります。 さて、読者はもしかしたら小学校や幼稚園などで Scratch とかVISCUIT とかのプログラミングを習ったかもしれませんが、2020年の時点では、これらは一般のIT企業などの実務では使われません。 Scratch とか VISCUIT とか、ああいうプログラミングは、「ビジュアルプログラミング」と言われていますが、「ブロックプログラミング」と言う場合もあります。 ※ マイクロソフトの Visual Basic や Visual C++ などとは違います。Visual Basic などは、幼児教育用には設計されていません。 さてに、Scratch などのブロックプログラミングを、ロボットプログラミングにも使えるのでは？と考えている人が既にいて、そういうブロックプログラミングできるロボット教材を販売している日本企業もすでにあります（アーテックロボ）。 書籍での文献は見つからなかったのですが、ソニー系のKOOVというロボット教材でも、webサイトで調べたかぎりでは、ブロックプログラミングがあります。 マイコン基盤のラブベリーパイにも、Scratchでプログラミングできるソフトウェアがあります。 なお、いずれのロボットも、ロボットのプログラミングにはパソコンが必要です。ロボット本体のコンピュータとは別に、パソコンが必要になります。（もしかしたらスマホでも出来るのかもしれないが、些末なツッコミになるので省略する。） おおむねの手順として、 パソコンに専用ソフトをインストールしてロボット用プログラムを書き、 そのプログラムを通信ケーブルなどでロボットに書き込む、 ような手順になっているだろうと思います。 詳しくは、それぞれのロボット教材をお調べください。

つくりながら学ぶ

技術を学ぶさい、安全などに配慮した上で、実際に作ってみるのが、いちばんラクに学べる方法であり、これはロボットなどを作る場合でも同じです。 とりあえずの機能だけでいいので、つくるための最低限の勉強だけをして、あとは実際に手を動かしてみて作るのがコツです。 大きなものを作る場合は、まずミニチュアを作ってみるのが良いでしょう。 ロボット教育の教材では、レゴブロックのような再利用の可能なブロックを構造材にしているものもあります。こういうブロックを活用すれば、資源の無駄も無くなります。 作っている途中、どうしても分からないところが出てきたら、そこでネットを確認したり、関連書籍を確認したりすると、効率的に知識を獲得できます。 ※ きみたち、スマホでも何でもいいけど、家電を使うときに、いちいち説明書を全部読まないでしょ？（例外的に読む人もいるが）　それと同じです。　先に操作してみて、あとで気になった知識を学ぶのです。 ※　例外的に、危険物をあつかう業界などでは、安全対策などのための知識が先に必要です。ですが、中学レベルのロボット学習では、そこまで危険なものを扱わないと思います。裏を返すと、安全対策などの知識は、先に学んでおいてください。 ここでいう「らせん」とは、こういう3次元の　らせん　のこと 技術的な知識は、それを単に字面を覚えるだけでは駄目であり、自分の理論的な知識が本当かどうかを、実際にものを作ってみて確認してみるという、理論と実験が必要です。。 そして、実際に手を動かして確認してみることで、今までの自分の知識の理解が深まります。そうなることで、さらに深い学習をできるようになり、前よりも上の知識を効率的に獲得できるようになります。 人生で、まるで、らせん階段を上っていくかのように、理論と実験を繰り返していくことになります。。 親柱付非常階段（マンハイム大学） キレスベルク塔の二重螺旋階段 コペンハーゲンの螺旋階段 そして、いちど実験をしてみて新たな知識が獲得できたので、それをもとに新しいアイデアが浮かび、さらに新しいものを作ることにつながります。こうして、一段階上の知識すら、また実験によって検証されます。 そして、実験によって自分の知識が検証されたことで、ますます理解が深まり、実用的な知識が増えていきます。そして、そのますます上達した知識をもとに、もっと新しいものを作れる・・・の繰り返しです。