この章では、2年生で学んだ三角形と四角形の性質をもとにして、円周角と中心角の性質を扱います。
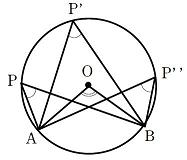 円周角と中心角
円周角と中心角
中心がOである円を円Oと呼ぶ。円Oにおいて、円周上の2点A , Bをとったとき、AからBまでの円周の部分を 弧AB (こAB)といい、![{\displaystyle {\begin{array}{c}\frown \\[-9pt]\scriptstyle {\rm {AB}}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b623c1b9cc8cefc39bbe235ce92e0b0e02eea8a) と書く。
と書く。 を弧ABに対する 中心角(ちゅうしんかく) という。また、弧ABを中心角
を弧ABに対する 中心角(ちゅうしんかく) という。また、弧ABを中心角  に対する弧(こ)という。
に対する弧(こ)という。
円Oの周上の点で、弧AB上にはない点Pをとったとき、 を弧ABに対する 円周角(えんしゅうかく) という。また、弧ABを円周角
を弧ABに対する 円周角(えんしゅうかく) という。また、弧ABを円周角  に対する弧という。
に対する弧という。
右の図のように、弧ABに対する円周角は  のようにいくつもできる。しかし、弧ABに対する中心角
のようにいくつもできる。しかし、弧ABに対する中心角  は1つに決まる
は1つに決まる
中心角と円周角には次の性質がある。
| 円周角の定理
|
|
1つの弧に対する円周角の大きさは一定であり、その弧に対する中心角の半分である。
|
この定理を証明するためには、円Oの弧ABに対する円周角の1つを  として、
として、 を示せばよい。
を示せばよい。
中心Oが 直線PAまたは直線PB上にある場合
[編集] 中心Oが
中心Oが  の辺上にある場合
の辺上にある場合
Oが直線PB上にある場合について示せば十分である。 は
は  の外角であるから、三角形の1つの外角はそれととなり合わない2つの内角の和に等しいので
の外角であるから、三角形の1つの外角はそれととなり合わない2つの内角の和に等しいので

 の辺OP , OAは等しいから
の辺OP , OAは等しいから

(1)、(2)より

したがって

よって、中心Oが 直線PB上にある場合、 が成り立つ。
が成り立つ。
 中心Oが
中心Oが  の内部にある場合
の内部にある場合
直線POと円Oとの交点のうちPでない方をCとすると、 は
は  の外角であるから
の外角であるから

 の辺OP , OAは等しいから
の辺OP , OAは等しいから

したがって

 は
は  の外角であるから
の外角であるから

 の辺OP , OBは等しいから
の辺OP , OBは等しいから

したがって

(1)と(2)の左辺どうしと右辺どうしをそれぞれ加えると

したがって

すなわち

よって、中心Oが  の内部にある場合、
の内部にある場合、 が成り立つ。
が成り立つ。
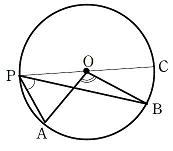 中心Oが
中心Oが  の外部にある場合
の外部にある場合
直線POと円Oとの交点のうちPでない方をCとすると、 は
は  の外角であるから
の外角であるから

 の辺OP , OAは等しいから
の辺OP , OAは等しいから

したがって

 は
は  の外角であるから
の外角であるから

 の辺OP , OBは等しいから
の辺OP , OBは等しいから

したがって

(1)と(2)の左辺どうしと右辺どうしをそれぞれひくと

したがって

すなわち

よって、中心Oが  の外部にある場合、
の外部にある場合、 が成り立つ。
が成り立つ。
以上で考えられるすべてのPの位置について証明されたので、「1つの弧に対する円周角の大きさはすべて等しい」ことが成り立つことがわかった。
半円の弧に対する中心角は  であるから、円周角は
であるから、円周角は  である。半円の弧に対する弦は直径であるから、次の定理が得られる。
である。半円の弧に対する弦は直径であるから、次の定理が得られる。
| 直径と円周角(ターレスの定理)
|
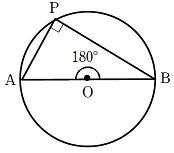
線分ABを直径とする円の周上にA、Bと異なる点Pをとれば

である。
|
 円周角と弧
円周角と弧
右の図の円Oで、円周角  が等しい場合、円周角の定理により
が等しい場合、円周角の定理により


となる。
 であるから、(1)、(2)より
であるから、(1)、(2)より

となる。
1つの円において等しい中心角に対する弧の長さは等しいので、
![{\displaystyle {\begin{array}{c}\frown \\[-9pt]\scriptstyle {\rm {AB}}\end{array}}={\begin{array}{c}\frown \\[-9pt]\scriptstyle {\rm {CD}}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06f459dfdfeb3cb613faf4ed62d7692cd71518f0)
が成り立つ。
また、右の図の円Oで、![{\displaystyle {\begin{array}{c}\frown \\[-9pt]\scriptstyle {\rm {AB}}\end{array}}\ ,\ {\begin{array}{c}\frown \\[-9pt]\scriptstyle {\rm {CD}}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b305f59e5ac02f13b2f884e37575d0e28c1842f6) が等しい場合、1つの円において等しい長さの弧に対する中心角は等しいので
が等しい場合、1つの円において等しい長さの弧に対する中心角は等しいので

となる。
よって、円周角の定理により

が成り立つ。
| 円周角と弧
|
|
1つの円において
- 等しい円周角に対する弧は等しい。
- 等しい弧に対する円周角は等しい。
|
高等学校数学A/図形の性質#円周角の定理の逆も参照。
円Oの周上の点をA,B,Cとし、 とする。また、直線ABについて点Cと同じ側に点Pをとる。このとき、Pが円Oの周上、内部、外部にある場合について、
とする。また、直線ABについて点Cと同じ側に点Pをとる。このとき、Pが円Oの周上、内部、外部にある場合について、 と
と  との大きさを比べる。
との大きさを比べる。
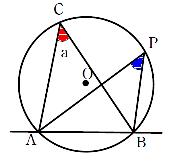 点Pが円Oの周上にある場合
点Pが円Oの周上にある場合
円周角の定理により

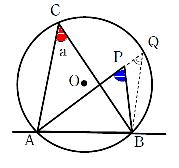 点Pが円Oの内部にある場合
点Pが円Oの内部にある場合
APの延長と円周の交点をQとする。 は
は  における
における  の外角であるから
の外角であるから

となる。
円周角の定理により、 であるから、
であるから、

よって

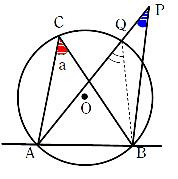 点Pが円Oの外部にある場合
点Pが円Oの外部にある場合
APと円周の交点をQとする。 は
は  における
における  の外角であるから
の外角であるから

となる。
円周角の定理により、 であるから、
であるから、

式を変形すると

よって

上で調べたことから、点Pを直線ABについて点Cと同じ側にとったとき

ならば、点Pは円Oの周上にあることがわかった。したがって、円周角の定理の逆として次のようにまとめられる。
| 円周角の定理の逆
|
 円周角の定理の逆 円周角の定理の逆
4点A,B,P,Qについて、P,Qが直線ABについて同じ側にあるとき,

ならば,この4点は1つの円周上にある。
|
まずは1年生で学んだ円の接線について復習する。
直線が円とただ1点で出あうとき、この直線は円に接する(せっする)といい、この直線を円の 接線(せっせん) といい、出あう1点を 接点(せってん) という。
| 円の接線
|
 円の接線 円の接線
円の接線は、接点を通る半径に垂直である。
|
 円外の点からの接線
円外の点からの接線
円O外の点Aから円Oにひけたとし、その接点をP,P'とする。
AP,AP'は円Oの接線であるから、


であるから、点P,P'はAOを直径上とする円周上にあることがわかる。
このことをふまえて、円O外の点Aから円Oに接線をひくには、次のようにすればよい。
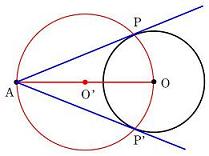 円外の点からの接線のひき方
円外の点からの接線のひき方
- 点AとOを結ぶ。
- 線分AOの垂直二等分線をひき、AOとの交点をO'とする。
- 点O'を中心として半径OO'の円を書き、円Oとの交点をP,P'とする。
- 直線AP,AP'をひく。
 接線の長さの証明
接線の長さの証明
 と
と  において
において
AP,AP'は接線だから

共通な辺だから

円Oの半径だから

(1)、(2)、(3)より斜辺と他の1辺がそれぞれ等しいから

したがって、
線分APまたはAP'の長さを、Aから円Oにひいた接線の長さという。
上で調べたことから、次のようにまとめられる。
| 接線の長さ
|
|
円外の1点からその円にひいた2つの接線の長さは等しい。
|















![{\displaystyle {\begin{array}{c}\frown \\[-9pt]\scriptstyle {\rm {AB}}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b623c1b9cc8cefc39bbe235ce92e0b0e02eea8a)




























![{\displaystyle {\begin{array}{c}\frown \\[-9pt]\scriptstyle {\rm {AB}}\end{array}}={\begin{array}{c}\frown \\[-9pt]\scriptstyle {\rm {CD}}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/06f459dfdfeb3cb613faf4ed62d7692cd71518f0)
![{\displaystyle {\begin{array}{c}\frown \\[-9pt]\scriptstyle {\rm {AB}}\end{array}}\ ,\ {\begin{array}{c}\frown \\[-9pt]\scriptstyle {\rm {CD}}\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b305f59e5ac02f13b2f884e37575d0e28c1842f6)

























