ここでは、三角形や円の性質、空間図形の性質等について扱う。
m, nを正の数とする。点Pが線分AB上にあってAB:PB=m:nが成り立つとき、「点Pは線分ABをm:nに内分する」という。
また、点Qが線分ABの延長線上にあってAQ:BQ=m:nであるとき、「点Qは線分ABをm:nに外分する」という。
 の辺AB, AC(またはその延長線)上にそれぞれ点P, Qがあるとき、次のことが成り立つ。
の辺AB, AC(またはその延長線)上にそれぞれ点P, Qがあるとき、次のことが成り立つ。



三角形の内角の2等分線に関して、次のことが成り立つ。
| 三角形の内角の2等分線と辺の比
|
|
 の の  の2等分線と辺BCとの交点をDとすると、Dは辺BCを内分する。 の2等分線と辺BCとの交点をDとすると、Dは辺BCを内分する。
|
 の2等分線と辺BCとの交点がDだから
の2等分線と辺BCとの交点がDだから

Cを通りADに平行な直線とBAの延長との交点をEとする。
ADとECは平行であるから


上の3つの式から

よって
 ……(1)
……(1)
また、ADとECは平行であるから
 ……(2)
……(2)
(1)と(2)より

三角形の外角の2等分線に関して、次のことが成り立つ。
Cを通りADに平行な直線とABの延長との交点をEとすると、上の定理と同様に

この二つの定理は角の二等分線定理と呼ばれている。
w:五心も参照。
- 三角形の外心
| 三角形の外心
|
- 定理
三角形の3つの辺の垂直二等分線は1点で交わる。
|

- 証明
△ABCを取り、辺AB,AC のそれぞれに対して垂直二等分線を取り、2直線の交点をOとする。このとき、点OがAB,ACのそれぞれに対する垂直2等分線上にあることから
 かつ
かつ 
であるので、

が成り立つ。
よって点Oは辺BCの垂直二等分線上にある。

上の証明から、 であるので、この点は三角形の3つの頂点から等距離にあることが分かるので、この点Oを中心として円を書くと、三角形ABCの頂点3つを通る円を書くことができる。
であるので、この点は三角形の3つの頂点から等距離にあることが分かるので、この点Oを中心として円を書くと、三角形ABCの頂点3つを通る円を書くことができる。
このように、三角形の3つの頂点を通る円(右図では赤線の部分)のことを外接円(がいせつえん、 英:circumscribed circle)という。
そして、外接円の中心(右図の点Oの部分)のことを、その三角形の 外心(がいしん)という。
- 三角形の内心
| 三角形の内心
|
|
三角形の3角のそれぞれに対して角の2等分線を取ったとき、それぞれの直線は1点で交わる。
|
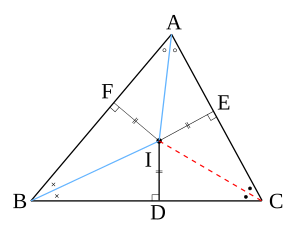
△ABCを取り、角A,Bについて角の2等分線を取り2直線の交点をIと呼ぶ。
さらに、点Iから辺BC,CA,ABに下ろした垂線とそれぞれの辺の交点をそれぞれ D,E,F と呼ぶとする。このとき、角Aの二等分線の性質から

が成り立ち、同様に角Bの2等分線の性質から

が成り立つので、
よって

である。
したがって、点Iは角Cの二等分線上にある。

ID=IE=IF なので、図のように三角形の三辺に接する円を書くことができ。この円を △ABCの内接円 (ないせつえん、英:inscribed circle)といい、その中心Iを内心(ないしん)という。
なお、三角形の内接円の半径をrとすると、面積Sと三辺の長さa,b,cとの間に

の関係式が成り立つ(△ABI、△BCI、△CAIの3つの三角形の面積を考えてみよ)。面積Sはヘロンの公式を用いれば、三角形の三辺の長さから内接円の半径が計算できる。
- 三角形の重心
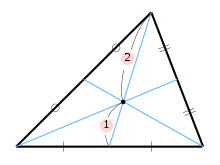
三角形の頂点から相対する辺の中点に対して下ろした線分のことを 中線 という。三角形の3つの中線の交わる点を重心という。
| 三角形の重心
|
 三角形の重心 三角形の重心
- 定理
三角形の3本の中線は1点で交わる。また、その交点は中線を 2:1 に内分する。
|
証明
 の辺BC, CA, ABの中点をそれぞれL, M, Nとする。
の辺BC, CA, ABの中点をそれぞれL, M, Nとする。
中点連結定理よりML // AB, 2ML=ABが成り立つので、中線AL, BMの交点をGとするとAG:GL=AB:ML=2:1
中線ALとCNの交点をG'とすると、上と同様に考えてAG':G'L=AC:NL=2:1
よって、GとG'はともに線分ABを2:1に内分する点であるので、この2点は一致する。
したがって、3本の中線は1点Gで交わり、AG:GL=2:1である。
同様にBG:GM=CG:GN=2:1なので、Gは各中線を2:1に内分する。
(※ 高校数学の範囲外)「重心」の力学的なバランス

- ※ 2019年現在では高校の理科で 重心 の力学的な意味を習うが、過去のカリキュラムでは中学の数学で後述の話題を扱っていた時代がある。
厚めの画用紙などで三角形をつくり、その三角形を水平にして、右図のように三角形の重心の部分で、棒で支えると、
水平方向の重さのバランスがとれるので、三角形を水平に保つことができる。
そもそも、このように重さのバランスを取れる場所であるので「重心」という名前がついている。重心の英語の center of gravity という英単語も、「重力の中心」という意味である。
理科の「物理」科目で習う「重心」とは、この例のように、重さのバランスを取れる部分という意味である。
なお、このような力学的な「重心」については、三角形だけでなく四角形や五角形などでも、同様に水平方向の重さのつりあいをとれる点として、力学的に「重心」を定義できる。
また、平面図形だけでなく立体図形でも同様、力学的に「重心」を定義できる。
- 三角形の垂心

外心の性質を利用して、次の定理が証明できる。
| 三角形の垂心
|
- 定理
三角形の各頂点から対辺またはその延長に降ろした垂線は、1点で交わる。
|
- 証明

点Aを通り辺BCに平行な直線、点Bを通り辺CAに平行な直線、点Cを通り辺ABに平行な直線をかき、これらの直線の交点を図のようにP,Q,Rとする。
すると、四角形RBCA は平行四辺形なので、 RA = BC である。
同様に、四角形ABCQ も平行四辺形なので BC=AQ である。
よって RA=BC かつ BC=AQ なので、 RA = AQ である。
次に、点Aから対辺BCまたはその延長上に垂線ADを引く。
すると、 RQ // BC の仮定により、平行な2直線の同位角が等しい事を利用して、
- AD ⊥ RQ
が導かれる。したがって、この線分ADは、△RQPの辺RQの垂直二等分線である。
同様に考えると、頂点Bから辺ACまたはその延長上に降ろした垂線BEは辺RPの垂直二等分線であり、頂点Cから辺ABまたはその延長上に降ろした垂線CFは辺PQの垂直二等分線であることがわかる。
この3本の垂直二等分線は、△RQPの外心で交わる。すなわち△ABCの各頂点から対辺に引いた3本の垂線 AD,BE,CF は一点で交わる。
ここまで三角形の外心、内心、重心、垂心を見てきた。実は正三角形の場合、この4点は一致することが知られている。
- 問題
- 以下の手順で、上記について証明せよ
- 重心と外心が一致する三角形は正三角形であることを証明する
- 重心と内心が一致する三角形は正三角形であることを証明する
- 内心と垂心が一致する三角形は正三角形であることを証明する
- 重心と外心が一致するならば重心と内心が一致し、さらに内心と垂心が一致することを述べる
また、正三角形でない三角形について外心O・重心G・垂心Hは常に一直線上に存在し、この直線をオイラー線と呼ぶ。
なお、オイラー線の証明は三角関数やベクトルでもできる。
オイラー線はw:九点円の中心Nも通り、ON=NHが成り立つ。
- 三角形の傍心
| 三角形の傍心
|

- 定理
三角形の2つの外角のそれぞれの二等分線と、残りの1つの内角の二等分線とは、一点で交わる。
|
- 証明

外角Bと外角Cの二等分線の交点をJとする。
図のように、Jから△ABCの3辺またはその延長線上に垂線JD,JE,JFをおろす。
すると、
- JF=JD かつ JE=JD
なので、
- JF=JE
である。
よって、直線AJは∠Aの二等分線である。
この点 J を 傍心(ぼうしん)という。
三角形には3つの傍心が存在する。
三角形の外心、内心、重心、垂心、傍心を合わせて三角形の五心と呼ぶ。

三角形  に対し、任意の一点
に対し、任意の一点  と
と  を結んだ直線がそれぞれ
を結んだ直線がそれぞれ  と交わる点を
と交わる点を  とする。
とする。
このとき、  が成り立つ。
が成り立つ。
証明
点  を通り直線
を通り直線  に平行な直線をかき、
に平行な直線をかき、 との交点をそれぞれ
との交点をそれぞれ  とする。
とする。



したがって、

平行線による比の移動より、 
- チェバの定理の逆
三角形  に対し、直線
に対し、直線  上にそれぞれ点
上にそれぞれ点  があるとき、
があるとき、 ならば、直線
ならば、直線  は一点で交わる。
は一点で交わる。
証明
直線  の交点を
の交点を  とおき、直線
とおき、直線  と直線
と直線  との交点を
との交点を  とおく。このとき、チェバの定理より、
とおく。このとき、チェバの定理より、 が成り立つ。また、仮定より、
が成り立つ。また、仮定より、 である。これら2つの式から、
である。これら2つの式から、 が得られる。これは、2点
が得られる。これは、2点  が線分
が線分  を同じ比で内分する点であることを示すので、 点
を同じ比で内分する点であることを示すので、 点  と点
と点  は一致する。よって、直線
は一致する。よって、直線  は一点で交わる。
は一点で交わる。
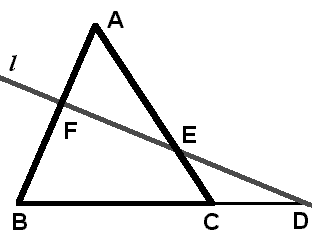
任意の直線  と三角形
と三角形  において、直線
において、直線  と直線
と直線 の交点をそれぞれ
の交点をそれぞれ とする。このとき
とする。このとき

が成り立つ。
証明
点  から直線
から直線  に平行な直線をかき、直線
に平行な直線をかき、直線  との交点を
との交点を  とする。
とする。
平行線による比の移動より、


したがって、
 [1]
[1]
- メネラウスの定理の逆
三角形  に対して、直線
に対して、直線  上に点
上に点  をとり、
をとり、 のうち三角形
のうち三角形  の辺上にある点が0個あるいは2個で、かつ、
の辺上にある点が0個あるいは2個で、かつ、 が成り立つとき、3点
が成り立つとき、3点  は一直線上にある。
は一直線上にある。
証明
2直線  の交点を
の交点を  とする。このとき、メネラウスの定理より、
とする。このとき、メネラウスの定理より、 である。また、仮定より
である。また、仮定より  である。これら2式より、
である。これら2式より、 である。これは、2点
である。これは、2点  が線分
が線分  を同じ比で内分する点であることを示すので、 点
を同じ比で内分する点であることを示すので、 点  と点
と点  は一致する。したがって、3点
は一致する。したがって、3点  は一直線上にある。
は一直線上にある。
三角形の辺と角の大小関係について、次のようなことが言える。
| 三角形の辺と角の大小
|
|
 において において

|
( の証明)
の証明)
 とし、辺AC上に点Dを、
とし、辺AC上に点Dを、  となるようにとれば
となるようにとれば
 ……(1)
……(1)
ところで、 は
は  の
の  の外角だから
の外角だから
 ……(2)
……(2)
また、点Dは辺AC上にあるから
 ……(3)
……(3)
(1),(2),(3)より、
( の証明)
の証明)
 であって、
であって、 ではないとすると、次のどちらかが成り立つ。
ではないとすると、次のどちらかが成り立つ。
 ……(1)
……(1) ……(2)
……(2)
(1)が成り立つとすると、二等辺三角形になるので、
(2)が成り立つとすると、前半で示したとおり、
どちらの場合も、仮定  に反する。
に反する。
よって、 でなければならない。
でなければならない。
三角形の3辺について、次のようなことが言える。
| 三角形の2辺の和
|
|
三角形の2辺の和は、残りの辺よりも大きい。
|
 において、
において、 を証明する。
を証明する。
辺BAをAの方に延長し、その上に点Dを、 となるようにとる。
となるようにとる。
 は二等辺三角形であるから
は二等辺三角形であるから

 において、点Aは辺BD上にあるから
において、点Aは辺BD上にあるから

よって、三角形の辺と角の大小の定理より

 の3辺の長さを、
の3辺の長さを、 とすると、上の定理より次のことがわかる。
とすると、上の定理より次のことがわかる。

| 三角形の2辺の差
|
|
三角形の2辺の差は、残りの辺よりも小さい。
|

であるから、 のとき、
のとき、 より
より

 のとき、
のとき、 より
より

が成り立つ。
2つの定理より、三角形の3辺が  であるとき、
であるとき、

が成り立つことがわかる。
逆に、正の数  が不等式
が不等式  を満たすとき、3辺の長さが
を満たすとき、3辺の長さが  である三角形が存在する。
である三角形が存在する。
この不等式を三角不等式と呼ぶ。
円周上に3点A,B,Cがある。直線ABについて点Cと同じ側に点Pをとり、 と
と  の大きさを比べる。
の大きさを比べる。
点Pについては、
- (1) Pが円周上にある
- (2) Pが円の内部にある
- (3) Pが円の外部にある
のいずれかである。
(2)の場合、三角形の外角と内角の間の大小関係より

(3)の場合も、三角形の外角と内角の間の大小関係より

この結果、次のことがいえる。
- (1) Pが円周上にある

- (2) Pが円の内部にある

- (3) Pが円の外部にある

このことから、次のようなことがいえる。
| 円周角の定理の逆
|
|
2点C,Pが直線ABについて同じ側にあるとき、 ならば、4点A,B,C,Pは同じ円周上にある。 ならば、4点A,B,C,Pは同じ円周上にある。
|
上の議論から三角形に外接する円はどのような三角形を取ったとしても常に存在
することが分かった。しかし、四角形に関してはそれに対して外接するような
円は常に存在するわけではない。
一般に円に内接するような四角形に関しては以下の性質が成り立つ。
| 円に内接する四角形の性質(1)
|
|
円に内接する四角形の相対する角の和は となる。 となる。
|
内接する四角形の頂点を反時計回りにA,B,C,Dとする。
このとき、角A,角Cはそれぞれ点B,Dを対応する端点とする円弧に対する円周角となっている。ただし、角Aと角Cは互いに逆の円弧を対応する弧としているため、2つの弧を合わせるとそれらの弧はちょうど円周をおおうことになる。
このため、これらの2つの弧に対応する中心角の和は に対応し、同じ弧に対応する円周角の和は
に対応し、同じ弧に対応する円周角の和は
 に対応するのである。
に対応するのである。
また、円に内接する四角形に関して以下の性質も成り立つ。
| 円に内接する四角形の性質(2)
|
|
円に内接する四角形において、1つの内角は、それに向かい合う内角の隣にある外角に等しい。
|
円に内接する四角形ABCDにおいて、上の定理より

また、頂点Cにおける外角を  とすると、
とすると、 であるから
であるから

円に内接する四角形の性質の逆について考えてみよう。
| 四角形が円に内接する条件
|
|
(1) 向かい合う内角の和が の四角形は、円に内接する。 の四角形は、円に内接する。
(2) 1つの内角が、それに向かい合う内角の隣にある外角に等しい四角形は、円に内接する。
|
(1)の証明
四角形ABCDで、
 …(I)
…(I)
とする。
 の外接円Oを書き、円Oに内接する四角形ABCD'を作ると
の外接円Oを書き、円Oに内接する四角形ABCD'を作ると
 …(II)
…(II)
(I),(II)より

したがって、円周角の定理の逆から、点Dはこの円Oの周上にある。
よって、四角形ABCDは円に内接する。
(2)の証明
四角形ABCDで、頂点Cにおける外角を  として、
として、

とする。

であるから

四角形が円に内接する条件(1)より、向かい合う内角の和が であるから、四角形ABCDは円に内接する。
であるから、四角形ABCDは円に内接する。
円Oの外の点Aからその円に2本の接線を引ける。その接点をP,Qとするとき、線分AP,AQの長さを、円Oの外の点Aから円Oに引いた接線の長さという。
2つの接線の長さについて、次のことがいえる。
| 接線の長さ
|
|
円外の点からその円に引いた2本の接線の長さは等しい。
|
直角三角形APO,AQOにおいて
 …(I)
…(I)
 は共通 …(II)
は共通 …(II)
(I),(II)より

よって、対応する辺APとAQは等しい。
円周上の点Aを通る接線ATがあって、円周上に2点B,Cをとるとき、 と円周角
と円周角  の大きさには、次のような関係がある。
の大きさには、次のような関係がある。
| 接弦定理
|
|
円の弦とその一端から引いた接線とのなす角は、その角内にある弧に対する円周角に等しい。
|
 が鋭角の場合について考える。
が鋭角の場合について考える。
直径ADを引くと、 であるから、
であるから、
 …(I)
…(I)
また、ADは直径であるから

 …(II)
…(II)
 と
と  は弧BDに対する円周角であるから
は弧BDに対する円周角であるから
 …(III)
…(III)
(I),(II),(III)より

 が直角、鈍角の場合についても同様に証明できる。
が直角、鈍角の場合についても同様に証明できる。
中心Oとする円について次の定理が成り立つ。
| 方冪(ほうべき)の定理
|
|
円周上に異なった2点A,Bを取りその2点を通る直線を取る。また、同様に
A,Bと異なった2点C,Dを通りそれらを通過する直線を取り、直線ABと直線CDの
交点をEと取る。このとき、

が成り立つ。この定理を方冪の定理と呼ぶ。
|
まず、点Eが円の外部にある場合を考える。このとき、直線AB上で点Eに近い点を点B,
直線CD上で点Eに近い点を点Cとおいたとき、三角形ECBと三角形EADが相似であることを
示す。
まず、四角形ABCDは円に内接していることから、

について、

が成立する。これは円に内接する四角形の相対する角の和が になることに
よっている。同様にして
になることに
よっている。同様にして

が成立し、2角が等しいことから三角形ECBと三角形EADは相似となる。
このことから、

となるが、このことは

に等しい。
次に、点Eが円の内部にある場合を考える。
このとき三角形EADと三角形EBCが互いに相似であることを示す。
最初に

についてこれらが互いの対頂角であることから

が成り立つ。次に、

についてこれらが円周BDの円周角であることから

が成り立つ。よって、2角が等しいことから三角形EADと三角形EBCは
互いに相似である。このことから

となるが、このことは

に等しい。
よって、どちらの場合にも方冪の定理が示された。
また、中心Oとする円の弦と接線について次の定理が成り立つ。
| 方冪の定理(2)
|
|
円の弦ABの延長上の点Pから円に引いた接線をPTとする。このとき、

が成り立つ。
|
 と
と  において
において
接弦定理より
 …(II)
…(II) (共通) …(II)
(共通) …(II)
だから、 と
と  は相似
は相似
よって、

したがって、

- 方冪の定理の逆
2つの線分AB, CD(またはその延長線)が点Pで交わるとき、PA・PB = PC・PDならば4点A, B, C, Dは同一円周上にある。
PA・PB=PC・PDよりPA:PD=PC:PBが成り立つ。
また、 である。
である。
よって、 と
と は相似なので、
は相似なので、 である。
である。
したがって、円周角の定理の逆より、4点A,B,C,Dは同一円周上にある。
方冪の定理(2)の逆も成り立つ。
- 問題
- 一直線上にない3点A, B, T及び線分ABの延長線上にある点Pについて、
 ならば直線PTが3点A, B, Tを通る円の接線であることを証明せよ。
ならば直線PTが3点A, B, Tを通る円の接線であることを証明せよ。
2つの円を取ったときこれらはいくつかの仕方で関係する。2つの円の関係は2つの円の中心間の距離と、2円の半径によって定まる。
2円の距離をそれぞれ ,
, (
( ),中心間の距離を
),中心間の距離を とすると、2円の位置関係として
とすると、2円の位置関係として
 のとき、円2は円1に含まれている。
のとき、円2は円1に含まれている。 のとき、2つの円は内接している。
のとき、2つの円は内接している。 のとき、円2と円1は互いに交わっている。
のとき、円2と円1は互いに交わっている。 のとき、2つの円は外接している。
のとき、2つの円は外接している。 のとき、2円は離れている。
のとき、2円は離れている。
がある。
2つの円がただ1つの共有点をもつとき、この2つの円は接するといい、この共有点を接点(せってん、英:point of contact)という。
1つの直線が、2つの円に接しているとき、この直線を、2つの円の共通接線という。
 のとき、共通接線はない。
のとき、共通接線はない。 のとき、共通接線は1本。
のとき、共通接線は1本。 のとき、共通接線は2本。
のとき、共通接線は2本。 のとき、共通接線は3本。
のとき、共通接線は3本。 のとき、共通接線は4本。
のとき、共通接線は4本。
定規・コンパスのみを用いて、与えられた条件を満たす図形を描くことを作図という。ただし、「直線を引く」「円を描く」「コンパスで長さを転写する」以外の操作(定規で長さを測る等)は認められない。
したがって、2つの三角定規を用いて平行線を引くことは上の意味での作図ではない。
これまで学んだ三角形や円の性質を用いることで、さまざまな図形を作図することができる。
作図そのものが大問としてテストや入試に出ることはあまりないが、図形問題を考える際は正確に作図することが大切になってくる。この先、数学Ⅱ「図形と方程式」や、数学C「ベクトル」においても作図ができないと話にならない。「テストに出ないからほっとく」ではなく、この先の幾何分野で役立てるために、ぜひきちんと学んでほしい。
与えられた直線 上にない点Pを通り、
上にない点Pを通り、 に平行な直線を作図する。
に平行な直線を作図する。
 上に点Aをとり、Aを中心とする半径APの円を描く。このとき、円と
上に点Aをとり、Aを中心とする半径APの円を描く。このとき、円と の交点をBとする。
の交点をBとする。- P, Bを中心としてそれぞれ半径APの円を描き、Aと異なる交点をCとする。
- PとCを結ぶと、直線
 に平行な直線が描ける。
に平行な直線が描ける。
- 問題
- 直線
 と直線PCが平行である理由を説明せよ
と直線PCが平行である理由を説明せよ
与えられた線分ABをm:nに内分する点を作図する。
- Aを通り、線分ABと異なる直線
 を引く。
を引く。
 上にAC:CD=m:nとなるように点C, Dをとる。このとき、Cは線分AD上にとる。
上にAC:CD=m:nとなるように点C, Dをとる。このとき、Cは線分AD上にとる。- Cを通りBDに平行な直線を引くと、ABとの交点が求める点である。
- 問題
- 与えられた線分ABをm:nに外分する点の作図方法を説明せよ
長さ1の線分ABと長さa, bの二つの線分が与えられたとき、長さ の線分を作図する。
の線分を作図する。
- Aを通り、ABと異なる直線
 を引く。
を引く。
 上にAC=a, AD=bとなるような点C, Dをとる。ただし、Cは線分AD上にとる。
上にAC=a, AD=bとなるような点C, Dをとる。ただし、Cは線分AD上にとる。- Dを通りBCに平行な直線を引いて直線ABとの交点をEとすると、線分BEが求める線分である。
証明
BE=xとする。
BC // EDより1:x=a:bである。
この式を変形すると となる。
となる。
- 問題
- 長さ1の線分ABと長さa, bの2直線が与えられたとき、長さabの線分を作図せよ。
上の二つは、値a, bに対して商a/b, 積abの計算を作図で行なっていることになる。
長さ1の線分ABと長さaの線分が与えられたとき、長さ√aの線分を作図する。
- 線分ABのBを超える延長線上にBC=aとなる点Cをとる。
- 線分ACの垂直二等分線を描き、線分ACとの交点をOとして中心O, 半径OAの円Oを描く。
- Bを通り、直線ABに垂直な直線を引き、円Oとの交点をそれぞれD, Eとすると、線分BDが求める線分である。
証明
方冪の定理より、BA・BC=BD・BE
ここで、AB=1, BC=a, BD=BEなのでBD=a^2となり、
BD=√aとなる。
- 問題
- 長さ1の線分ABと長さa, bの二つの線分が与えられたとき、長さ
 の線分を作図せよ
の線分を作図せよ
正五角形について、一辺の長さと対角線の長さの比は黄金比1 :  である。ここで、
である。ここで、 は黄金数と呼ばれる数である。
は黄金数と呼ばれる数である。
長さ2の線分CDが与えられたとき、正五角形ABCDEを作図する。
まずは、対角線ACの長さが1+√5であることを利用して、頂点Aを作図する。
- 線分CDの垂直二等分線
 を引き、CDとの交点をPとする。
を引き、CDとの交点をPとする。
 上にPQ=CDとなるような点Qをとる。
上にPQ=CDとなるような点Qをとる。- 線分CQのCを超える延長線上に、QR=CPとなるような点Rをとる。
- Cを中心として半径CRの円を描くと、
 との交点がAである。このとき、CQ=√5, CA=CR=1+√5である。
との交点がAである。このとき、CQ=√5, CA=CR=1+√5である。
- 中心C, 半径CDの円と中心D, 半径ACの円の交点がBである。同様に、中心D, 半径CDの円と中心C, 半径ACの円の交点がEである。
ここでは、空間における直線・平面の位置関係について学ぶ。この内容は数学Cで空間ベクトルを学ぶ際に知っておかなければならない基礎的な知識である。
異なる2直線の位置関係には、
- 一点で交わる
- 平行である
- ねじれの位置にある
の3つの場合がある。
平面図形と同様、2直線l, mが平行なときl // mのように表す。
2直線l, mが平行でないとき、点Oを通りl, mにそれぞれ平行であるような2直線l', m'を引くと、l', m'は同一平面上にあり、そのなす角は点Oの取り方によらず一定である。この角を2直線l, mのなす角と呼ぶ。
この角が直角であるとき、「lとmは垂直である」といい、l ⊥ mのように表す。
特に、垂直な2直線が交わるとき、それらは「直交する」という。
また、平行な2直線の一方に垂直な直線は他方にも垂直である。
- 問題
- 立方体ABCD-EFGHにおいて、辺ABと平行な辺、垂直な辺、ねじれの位置にある辺をそれぞれ全て答えよ。
直線lと平面aの位置関係には、
- lはaに含まれる(lはa上にある)
- 一点で交わる
- 平行である
の3つの場合がある。
直線lと平面aが平行であるとき、l // aと表す。
直線lが平面a上の全ての直線に垂直であるとき、直線lは「平面aに垂直」または「平面aに直交」であるといい、l ⊥ aと表す。
特に、直線lが平面a上の交わる2直線m, nに垂直ならば、直線lは平面aに垂直である。
- 問題
- 正四面体ABCDにおいて辺CDの中点をMとしたとき、辺CDと平面ABMについてCD ⊥ ABMを示せ。また、AB ⊥ CDを示せ。
異なる2平面a, bの位置関係には、
- 一直線で交わる
- 平行である
の2つの場合がある。
2平面が交わるとき、共有する直線を交線と呼ぶ。
2平面a, bが平行であるとき、a // bと表す。
交わる2平面の交線上の点から各平面上に引いた、交線に垂直な2つの直線のなす角を2平面のなす角と呼ぶ。
2平面a, bのなす角が直角であるとき、a, bは「垂直である」または「直交する」といい、a ⊥ bと書く。
- 問題
- 平面aの一つの垂線を含む平面bについて、a ⊥ bであることを証明せよ
三角柱、四角錐などのように、多角形の面で囲まれた立体を多面体という。
凹みのない多面体を特に凸多面体と呼ぶ。
各面が全て合同な正多角形であり、各頂点に集まる面の数が全て等しい凸多面体を正多面体(プラトンの多面体)という。
正多面体は正四面体、正六面体(立方体)、正八面体、正十二面体、正二十面体の5種類のみ存在する。
- 問題
- 正四面体を二つ貼り合わせた6面体が正多面体でないことを説明せよ
正八面体について、
- 面の数は8である。
- 一つの面の頂点の数は3、一つの頂点に集まる面の数は4なので、頂点の数は

- 一つの面の辺の数は3、一つの辺に集まる面の数は2なので、辺の数は
 である。
である。
同様にして、正多面体について面の数・頂点の数・辺の数を計算で求めることができる。
- 問題
- 以下の表を完成させよ。また、各正多面体について、(頂点の数)-(辺の数)+(辺の数)を計算せよ。
| 正多面体 | 面の数 | 面の形 | 1頂点に集まる面の数 | 頂点の数 | 辺の数 |
|---|
| 正四面体 | | | | | |
|---|
| 正六面体 | | | | | |
|---|
| 正八面体 | 8 | 正三角形 | 4 | 6 | 12 |
|---|
| 正十二面体 | | | | | |
|---|
| 正二十面体 | | | | | |
|---|
| オイラーの多面体定理
|
|
一般の凸多面体について、頂点の数をv, 辺の数をe, 面の数をfとすると

が成り立つ。
|
また、一般の多面体について、次のことが言える。
- 多面体の一つの頂点に集まる面の数は3以上である。
- 凸多面体の一つの頂点に集まる角の大きさは360°よりも小さい。
つまり、正多面体の面になる正多角形の一つの内角の大きさは120°よりも小さい。そのような正多角形を考えると、正多面体の面になり得るのは正三角形、正方形、正五角形のみである。
この事実とオイラーの多面体定理を利用して、正多面体が5種類しか存在しないことを証明できる。
- 問題
- 正多面体が正四面体、正六面体、正八面体、正十二面体、正二十面体の5種類しか存在しないことを証明せよ。
余談だが、オイラーの多面体定理に似た式が四次元の正多胞体においても成り立つことが知られている。
多面体から切り取った立体が正多面体であることを利用することで、立体の体積を求めることができる。
- 問題
- 立方体ABCD-EFGHを4平面BDE, BEG, BGD, DEGで切り取ると正四面体BDEGができる。このことを利用して、一辺の長さがaである正四面体の体積を求めよ。
- ^
 を使って変形した
を使って変形した









































































































































































