小学校算数/2学年

1年生のふくしゅう

• もんだい

バスに人が、9人のっています。つぎのバスていで、7人ふえて、またつぎのバスていで3人がへりました。バスにのっている人数(にんずう)は何人(なんにん)でしょう。

このもんだいの答(こた)えは

$9+7-3$

というしきで もとめられます。こたえは13人です。

たし算とひき算のひっ算

たしざん の ひっさん

34 + 12 の　ような　けいさん を　するとき　に、

下　の　ような　けいさん　の　しかた　が　あります。

これを　ひっさん（筆算）　と　いいます。

				3	4
	＋			1	2
				4	6

十の くらい	一の くらい
3	4

たとえば、この 34＋12 の　ひっさん では、34 の「3」 の ぶぶん は、十（じゅう）の　くらい　です。

34 の「4」 の ぶぶん は、一（いち）の　くらい　です。

12 の、「1」のぶぶんは　十のくらい　です。

12 の、「2」のぶぶんは、一のくらいです。

このように、ひっさんを　かくときは　おなじ　くらい　どうしの　、たて　の　ならび　を　あわせて、かきます。

3の下に　1が　かいてあることに、きづいてください。

4の下に　2が かいてあることに、きづいてください。

ひっさんの　しかた

では、　たしざんの ひっさん　の　しかた　を　せつめいします。

まず、一のくらいの数(かず)をたして、下にかきます。4+2=6なので、6 とかきます。

つぎに、十のくらいの数をたして、下にかきます。3+1=4なので、4 とかきます。

こたえは 46 となります。

つぎは 53+29 を計算(けいさん)してしましょう。

				5	3
	＋			2	9

まず、一のくらいをたしあわせると 3+9=12 となりますが、そのままではかけません。

そこで、十のくらいに 1 くりあげて 一のくらいに 2だけかきます。

※ 「くりあげる」とは、このように、ひとつ上の　くらい　に　1　を　たすことを　いいます。

つぎに 十のくらいを たしあわせますが、くりあがりの 1 があるので 1 も たして　5+2+1=8 となります。

53+29のこたえは 82です。

				51	3
	＋			2	9
				8	2

ひきざん の ひっさん

			5	6
	－		3	2
			2	4

まず、一のくらいをひきます。 6-2=4 となります。下に 4 とかきます。

つぎに 十のくらいを ひきます。5-3=2 となります。下に 2 とかきます。

56-32のこたえは 24 です。

			76	1
	－		2	6
			4	5

まず、一のくらいをひくと 1-5 となりますが、ひけません。

そこで、5 だけかいて、十のくらいを 1 くりさげて 一のくらいに 3をけして 1ひいて 2 に します。

※ 「くりさげる」とは、ひとつ上の　くらい　から、1 を かりてくる ことです。

十のくらいを ひきます。6-2=4 となります。下に 4 とかきます。

71-26 のこたえは 45 となります。

			106
	－		3	7
			6	9

106 - 37 を考(かんが)えてみましょう。

まず、一のくらいを ひきざんします。しかし、6-7 はけいさんできません。下に 9 だけかいて、そこで、十のくらいを 1 くり下げます。しかし、十のくらいは 0　なので、くり下げられません。そこで、百のくらいから 1 くり下げます。百のくらいと 十のくらいの「10」を1 くりさげて 9 にします。そして、十のくらいをけいさんします。 9-3=6 なので、 6 をかきます。よって、こたえは 69です。

			1 096
	－		3	7
			6	9

かけざん

うさぎが、3ひき　います。うさぎには、1ひきで　2こずつ　耳が　ついています。うさぎの耳の数は、3ひきを　あわせて、ぜんぶで、耳は、いくつでしょうか。

かんがえかたは、いくつもあります。

• かんがえかた

うさぎが、3ひき、います。

そして、耳は、1ひき　に、2こ　ずつ　ついています。

なので、3ひき、ぜんぶでは、つぎのようになります。

• ほかの、かんがえかた

そして、耳は、1ひき　に、2こ　ずつ　ついています。

うさぎが、3ひき、います。

なので、3ひき、ぜんぶでは、つぎのようになります。

ほかにも、　しきは

$2+2+2$

と、あらわせます。

• かけざん

つぎのように、　かきます。

$2\times 3$

よみかたは、「に かける さん」　と、　よみます。

$2\times 3$ の　こたえは、　$2+2+2$　と　おなじです。　

たしざんの　しきと　こたえは　$2+2+2=6$ 　ですね。

なので $2\times 3$ の　こたえは

$2\times 3=6$

です。

たしざんの　しきと　こたえは　$2+2+2=6$ 　ですね。

なので $2\times 3$ の　こたえは

$2\times 3=6$

です。

「$2\times 3$」 のようなけいさん を　かけざん　と　いいます。

• かけざんの れんしゅう

うさぎが、5ひき　だと　しましょう。　このとき、　5ひき　ぜんぶを　あわせた　みみのかずは　いくつでしょう？

しきの、　

$2\times 5$

を、　もとめるには、　どうすれば、よいでしょうか？

このばあい、

$2+2+2+2+2=10$

で、　もとめることが、　できます。

---

• けいさん

$5\times 3$

を、計算してみましょう。

たとえば、うえの 図(ず)のように、かんがえた場合(ばあい)、こたえは 15 ですね。

---

• れんしゅう

8台(だい)の車に、子どもが、4人ずつのっています。ぜんぶで、子どもは、何人(なんにん)のっていますか。

• かんがえかた

車に、子どもは、4人のっていて、車は、8台ありますね。4人のっている車が8つ分（ぶん）あることから、4の8つ分といい、しきは、$4\times 8$になります。

「4かける8」とよみます。こたえのもとめかたは、4の8つ分なので、

${\begin{matrix}4+4+4+4+4+4+4+4&&\end{matrix}}$

と、たしざんでもとめます。こたえは、32です。

---

九九

$1\times 1$から、$9\times 9$まで、かけ算のしきは、たくさんあります。たとえば、$5\times 6$は、「五六(ごろく) 30」といいます。このようないいかたを、「九九(くく)」といいます。九九をおぼえると、生活(せいかつ)の中で、とてもやくに立ちます。

• 5のだん・2のだんの九九

五一(ごいち)が五(ご) $5\times 1=5$

五二(ごに) 十(じゅう) $5\times 2=10$

五三(ごさん) 十五(じゅうご) $5\times 3=15$

五四(ごし) 二十(にじゅう) $5\times 4=20$

• 3のだん・4のだんの九九

• 6のだん・7のだんの九九

• 8のだん・9のだんの九九

• 1のだんの九九

かけ算九九の表

	1	2	3	4	5	6	7	8	9
1	1	2	3	4	5	6	7	8	9
2	2	4	6	8	10	12	14	16	18
3	3	6	9	12	15	18	21	24	27
4	4	8	12	16	20	24	28	32	36
5	5	10	15	20	25	30	35	40	45
6	6	12	18	24	30	36	42	48	54
7	7	14	21	28	35	42	49	56	63
8	8	16	24	32	40	48	56	64	72
9	9	18	27	36	45	54	63	72	81

上の表は、九九(くく)の表(ひょう)です。もし$4\times 8$のばあいは、4と8のらんを見ていって、かさなるところが、答え（こたえ）に、なります。

1×1=1「いんいち　が　いち。」　1×2=2「いんに　が　に。」　1×3=3「いんさん　が　さん。」　1×4=4「いんよん　が　よん。」　1×5=5「いんご　が　ご。」　1×6=6「いんろく　が　ろく。」　1×7=7「いんなな　が　なな。」　1×8=8「いんはち　が　はち。」　1×9=9「いんく　が　く。」

ところで、=の、よみかたについて、 たしざんのときは

1+1=2

は「いち　たす　いち　は（わ）　に」　と　＝　を　「は」（わ）と、よんでいたのに、

なんで、　かけざんでは　

1×1=1「いんいち　が　いち。」

というふうに　= を　「が」　で　よむの？

と、いわれても、

とくに、　ふかい　りゆうは　ありません　。　

むかしからの　日本（にほん）での　九九（くく）の　よみかたで　、　このような　九九の　よみかたが　、　つたえられている　だけです　。

2×1=2「にいち　が　に。」　2×2=4「ににん　が　し。」　2×3=6「にさん　が　ろく。」　2×4=8「にし　が　はち。」　2×5=10「にご　じゅう。」　2×6=12「にろく　じゅうに。」　2×7=14「にしち　じゅうし。」　2×8=16「には　じゅうろく。」　2×9=18「にく　じゅうはち。」

3×1=3「さんいち　が　さん。」　3×2=6「さんに　が　ろく。」　3×3=9「さざん　が　く。」　3×4=12「さんし　じゅうに。」　3×5=15「さんご　じゅうご。」　3×6=18「さぶろく　じゅうはち。」　3×7=21「さんしち　にじゅういち。」　3×8=24「さんぱ　にじゅうし。」　3×9=27「さんく　にじゅうしち。」

4×1=4「しいち　が　し。」　4×2=8「しに　が　はち。」　4×3=12「しさん　じゅうに。」　4×4=16「しし　じゅうろく。」　4×5=20「しご　にじゅう。」　4×6=24「しろく　にじゅうし。」　4×7=28「ししち　　にじゅうはち。」　4×8=32「しは　さんじゅうに。」　4×9=36「しく　さんじゅうろく。」

5×1=5「ごいち　が　ご。」　5×2=10「ごに　じゅう。」　5×3=15「ごさん　じゅうご。」　5×4=20「ごし　にじゅう。」　5×5=25「ごご　にじゅうご。」　5×6=30「ごろく　さんじゅう。」　5×7=35「ごしち　さんじゅうご。」　5×8=40「ごは　しじゅう。」　5×9=45「ごっく　しじゅうご。」

6×1=6「ろくいち　が　ろく。」　6×2=12「ろくに　じゅうに。」　6×3=18「ろくさん　じゅうはち。」　6×4=24「ろくし　にじゅうし。」　6×5=30「ろくご　さんじゅう。」　6×6=36「ろくろく　さんじゅうろく。」　6×7=42「ろくしち　しじゅうに。」　6×8=48「ろくは　しじゅうはち。」　6×9=54「ろっく　ごじゅうし。」

7×1=7「しちいち　が　しち。」　7×2=14「しちに　じゅうし。」　7×3=21「しちさん　にじゅういち。」　7×4=28「しちし　にじゅうはち。」　7×5=35「しちご　さんじゅうご。」　7×6=42「しちろく　しじゅうに。」　7×7=49「しちしち　しじゅうく。」　7×8=56「しちは　ごじゅうろく。」　7×9=63「しちく　ろくじゅうさん。」

8×1=8「はちいち　が　はち。」　8×2=16「はちに　じゅうろく。」　8×3=24「はちさん　にじゅうし。」　8×4=32「はちし　さんじゅうに。」　8×5=40「はちご　しじゅう。」　8×6=48「はちろく　しじゅうはち。」　8×7=56「はちしち　ごじゅうろく。」　8×8=64「はっぱ　ろくじゅうし。」　8×9=72「はっく　しちじゅうに。」

9×1=9「くいち　が　く。」　9×2=18「くに　じゅうはち。」　9×3=27「くさん　にじゅうしち。」　9×4=36「くし　さんじゅうろく。」　9×5=45「くご　しじゅうご。」　9×6=54「くろく　ごじゅうし。」　9×7=63「くしち　ろくじゅうさん。」　9×8=72「くは　しちじゅうに。」　9×9=81「くく　はちじゅういち。」

ちなみに、かけざんの答(こた)えが９までなら九九に「が」が入り、10をこえたら入りません。

• れんしゅう

つぎの　もんだいを といて みましょう。

4×3 =

7×2 =

9×9 =

2×7 =

5＋9 =

7×8 =

7－2 =

3×9 =

• こたえ

4×3 = 12

7×2 =14

9×9 = 81

2×7 = 14

5＋9 = 14

7×8 = 56

7－2 = 5

3×9 = 27

もっと、もんだい　を　ときたい　ひと　は　、　「2ねんせいのためのさんすうドリル」　の　ページ　を　見に 行って（いって） ください。 した　の　「2ねんせいのためのさんすうドリル」の　もじ を　おすと、みている ページが ドリルのぺージに かわります。

• 2ねんせいのためのさんすうドリル

ながさ

cm(センチメートル)とmm(ミリメートル)

ながさをはかるときには、「ものさし」というどうぐを つかうことがあります。　

学校や　いえ（家）　で、　このような　めもり　が　ふってある　もの　を　みたことが　ある人も　いるでしょう。

これが　ものさし　です。

家の人 に　、おうち　にある　ものさし　を　みせてもらって　ください。

うえの ものさしの 図(ず)で、1めもり (「0」と「1」の あいだの ながさ) を 1cm(センチメートル)といいます。ながさは、1cmの いくつ分(ぶん)かで あらわします。

もし、　ものさし　が　ふたつ　いじょう　あれば　1cm　の ながさを くらべてみてください。

どのものさしも、　1cmのながさ　は、おなじに　なっている　でしょう。

このように、ながさのきじゅんはきまっています。 　 日本(にほん(にっぽん))じゅう、せかいじゅう どこでも、1cm は同(おな)じ 長(なが)さです。これは、きまりなので かってに　かえることは できません。

• 4cmは、ものさしの「0」と書かれたところから、「4」と書かれたところまでの長さです。

• mm(ミリメートル)は、1cmを同じ長さに10こにわけたものです。1cmは、10mmです。

• 2cm3mmは、2cmと 3mm のことです。

直線(ちょくせん)

ものさし で書いた、まっすぐな線(せん)のことを、「直線(ちょくせん)」といいます。

たとえば、「4センチメートルの直線」といったら、ものさしをつかって書かれた、ながさが4センチメートルのまっすぐな線（せん）のことです。

m(メートル)

100cmのことを 1m(メートル)ということがあります。 1mは100cmです。

1cm が　10mm でした。

なので、1mは　1000mm　です。

形(かたち)

ものには　いろいろな　形(かたち)のものが　あります。たとえば　あなたが 今(いま)見ているパソコンや タブレットなどの　がめんも 形です。

3本の　まっすぐな　せん　で　できていて　、　そのどれもが　むすばれている　かたちを　三角形(さんかくけい)といいます。下の図(ず)を見てみましょう。

• 一番(いちばん)左は、三角形　です。　まっすぐな3本の直線でできていて、ちゃんとほかの辺にむすばれています。
• まん中は、三角形 ではありません。　3本の　まっすぐな直線で　できていますが　うち2本のせんは　むすばれて　いません。
• 一番右は、三角形 ではありません。　3本は　ちゃんとむずばれていますが、　うち1本の　せん　は　まがって　います。

三角形　を つくっている　まっすぐ　な　直線(ちょくせん)　を　辺(へん) と　いいます　。

三角形　は　3ほん　の　へん　で　つくられています。

図形の角の点を ちょう点 といいます。

しかくけい

また、4ほんのまっすぐなせんでできていてそのどれもがむすばれているかたちをしかくけい（四角形）といいます。

• 
  * これも、しかくけい です。
• 
  * これも、しかくけい　です。
• 
  * これも、しかくけい　です。
• 
  * これも、しかくけい　です。

しかくけい　は　４ほん　の　、直線(ちょくせん)　から　できています　。

しかくけい　は　4ほん　の　へん　で　できています。

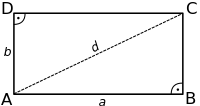
• ちょうほうけい

このような、かど　が　みんな 直角(ちょっかく)　である しかくけい　を、 ちょうほうけい 　（長方形）と　いいます。

• せいほうけい

この　ずけい　の　いろが　ついている　ところ　は　しかくけい　ですね。

このように、　かど　が　みんな ちょっかくで、へんのながさ　が　すべて　おなじ　しかくけいを　せいほうけい（正方形）　と　いいます。「ましかく」

せいほうけい

ちょっかく

下の図のような、かど が　せいほうけい（正方形）　の　かど（角）　や　ちょうほうけい（長方形）　の　かど（角）　と　おなじ　かど（角）　の　こと　を　ちょっかく（直角）　といいます。

1つの かどが　ちょっかくである三角形 のこと を　直角三角形　（ちょっかく さんかくけい） と、いいます。

10000までの数(かず)

かず　の　100 のことを 百 といいます。

かず　の　1000　の　こと　を　「千(せん)」と　いいます。

1000 は　かん字　で 千 と　かきます。

1000 の　こと を 一千 と　いう　ばあい　も　あります。

千（せん）　の　すうじ　1000 は、　1　の　うしろ　に、　0 が 3こ です。

1623 の よみかた　は　「せん ろっぴゃく にじゅう　さん」 です 。または、「いっせん ろっぴゃく にじゅう　さん」 です 。

2000 の よみかた　は　「にせん」 です 。

2025 の よみかた　は　「にせん にじゅう ご」 です 。

3000 の よみかた　は　「さんぜん」 です 。「さん せん」では なくて、「さん ぜん」です。

4000 の よみかた　は　「よんせん」 です 。

5000 の よみかた　は　「ごせん」 です 。

5000 の よみかた　は　「ごせん」 です 。

6000 の よみかた　は　「ろくせん」 です 。

7000 の よみかた　は　「ななせん」 です 。

8000 の よみかた　は　「はっせん」 です 。

9000 の よみかた　は　「きゅうせん」 です 。

かず　の　10000　の　こと　を　、「いち まん」と　いいます。

10000 は　かん字（漢字）　で 一万 と　かきます。

一万（いちまん）　の　すうじ　10000 は、　1　の　うしろ　に、　0 が 4こ です。

1から10000までの　けた　の　いいかた　を　いうと　

「いち　じゅう　ひゃく　せん　まん　」

となります。

声(こえ)にだして、おぼえましょう。

かさ

お店でかうことのできるジュースには、中にどれくらいジュースが入っているかを「mL」や「L」をつかって書いてあります。またガソリンスタンドでも車にどれくらいガソリンが入ったかをあらわすために「L」をつかいます。これらはジュースやガソリンなどのりょうをくらべるためにつかうたんいです。

「mL」は ミリリットル とよみ、「L」は リットル とよみます。また、「dL」は デシリットル とよみます。

1L は 10dL です。 また 1L は 1000mL です。 1dL は 100mL と なります。

1リットル　の　おおきさ　は　、せかいじゅう（世界中）　の　どこに　でかけても、おなじです。

なお、リットルをはかる　ための　いれもの　として　「リットルます」　という　もの　が　あります。

ふつう、1リットルのかさを　はかりやすいように　なっているので　「1リットルます」とも　いいます。

なお、デシリットルのための　ます　は「1デシリットルます」といいます。

バケツに、「1デシリットルます」を10っぱい　そそぐと、1リットル　の　かさ　になります。

きをつけよう

「1リットルます」には、10とう分　した　線（せん）が　あります。そして、その1Ｌのかさを　10とうぶん　したものが　1dL でした。

「1デシリットルます」には、10とう分　した線が　あります。　ですが、1デシリットルます　を　10とう分　したものは 10mL です。（1mL と　まちがえる人が、ときどき　いる。）

「ミリ」の おはなし

※ このワクの なかの ハナシ は、おぼえなくていいです。

「ミリリットル」の「ミリ」と、「ミリメートル」の「ミリ」は、おなじ　いみ　で、 「1000とうぶん　した」　という いみ です。千（せん）とうぶん です。

なので、1000ミリリットルは　1リットル　です。

なので、1000ミリメートルは　1メートル　です。

さて、「デシ」は、ながさ　では、めったに　つかわないのが　ふつう　です。

なので、「かさ」の「デシリットル」というように、リットルという　たんい　と　いっしょに　おぼえるように　しましょう。

また、「センチ」は、　かさ　では　めったに　つかわないのが　ふつう　です。

なので、「ながさ」の「センチメートル」というように、　メートルという　たんい　と　いっしょに　おぼえるように　しましょう。

むかし、リットル「L」を「ℓ」と　書くことが　ありました。

また、むかし、「mL」を、「cc（シーシー）」ということが　ありました。

いまはもう、あまり　「ℓ」　や「cc」 はつかわれなく　なりましたが、むかしは、つかわれていました。

かず の おおきさ くらべ

14 と 57 では、どちらが おおきい かず でしょうか。

57 のほうが 、おおきい ですね。

かず の おおきさ を くらべるとき、この 14 と 57 の ばあい は、

14 ＜ 57

と、かきます。 「14は、57より、小さい」

9 と 2 では、どちらが おおきい でしょうか。

9のほうが大きいです。

9 ＞ 2

と、かきます。

このように、大きさ（おおきさ）をくらべるときに「＞」や「＜」といった記号（きごう）をつかいます。

＞や＜を ふとうごう（不等号） と いいます。

「とうごう」（等号）とは 「＝」 のことです。 「ふとうごう」（不等号） の「ふ」（不）とは、「ちがう。」とか「そうではない。」という意味（いみ）です。

大きさが ちがう数（かず）を くらべるとき は、ちがう大きさなので、不等号（ふとうごう）の ＞ や ＜ をつかいます。

＞ と ＜ の 、つかいかた は、

大きな数（おおきなかず） ＞ 小さな数（ちいさなかず）

小さな数 ＜ 大きな数

です。

17 と 13+4 は、どちらが大きいでしょうか。

このばあい、13+4=17 なので、おなじ大きさです。

こういうばあい の 大きさ くらべ は、

17 = 13+4

と、かきます。

このばあい、大きさが、おなじ なので、ふとうごうの ＜ や ＞ は、つかえません 。

じこく

みなさんは、たとえば、今（いま） 何時（なんじ）か しりたい ばあい に 時計（とけい）を 見ますね。では、 時こく（じこく） と 時間（じかん） に ついて 学びましょう。時計とは、このしゃしんのようなものです。

ふん

時計の 長いはりが 1目もり（いち めもり） うごく あいだ が 1分 （いちふん） です。

たとえば、宿題（しゅくだい）を始めた 時こく が 4時 だったとします。ちなみに、「時こく」は、「3時」「4時」などの「たんい」のことです。では「分」の学習にもどりましょう。宿題がおわると、 4時15分 でした。

宿題を始めてから　何分　たったか　かんがえましょう。

さっき言ったように、長いはりが1目もり うごく あいだ が 1分 です。

4時 から 4時15分 に なるまで 15目もり うごきました。

こたえ　は　した　に　かいてあります。　 さきに　かんがえてから　、　こたえ　を　みて　ください。

答えは、15分（じゅうごふん） が たった の です。

じかん

つぎは、時間（じかん）について 学びましょう。 時間とは、時こくと時こくの間のことです。

たとえば、サッカーの 番組（ばんぐみ）が はじまった 時こく（じこく） は、7時（しちじ）でした。

サッカー の 番組（ばんぐみ） が おわった 時こく（じこく） は、10時(じゅうじ)でした。

サッカー の 番組（ばんぐみ） は 何分　ほうそう　していた　でしょう。

まず、時間　の　あたらしい　たんい　を 学びましょう。

短いはりが 一回り する あいだ は、1時間（いちじかん）です。

1時間 は、 60分（ろくじっぷん）です。

7時 から 10時 の あいだ に、長いはり の 一回り は　3回　ありました。

つまり、サッカーの 番組は 3時間(さんじかん) ほうそう していたのです。

1にち　の　ながさ

1にち　の　ながさ　は　24時間　です。

また、前(まえ)の12時間(じかん)を 午前(ごぜん)といい、後(あと)の12時間を 午後(ごご)といいます。

はこの形(かたち)

はこの形(かたち) について考えましょう。

長方形(ちょうほうけい)だけでできているはこ

• • ふでばこ などがありますね。

おなじ 大きさの 正方形(せいほうけい)だけでできているはこ

• • さいころ などがありますね。

分数(ぶんすう)

図(ず)のように、もとの大きさを2つに分(わ)けたうちの1つを${\frac {1}{2}}$とかき、2分(ぶん)の1 とよみます。

図のように、もとの大きさを3つに分(わ)けたうちの1つを${\frac {1}{3}}$とかき、3分(ぶん)の1 とよみます。

図のように、もとの大きさを4つに分(わ)けたうちの1つを${\frac {1}{4}}$とかき、4分(ぶん)の1 とよみます。

まぎらわしい　もんだい

つぎの　もんだい　を　といてみましょう。

「3人の　男の子と、　4人の女の子が　います。　男の子も女の子も、1年生（いちねんせい）です。

男の子たちは、あめだま　を あわせて　７こ　もっています。

女の子たちは、あめだま　を　あわせて　5こ　もっています。

あめだまは、　あわせて　なんこ　あるでしょうか。」

もんだいが　なにを　たずねているのか、　かんがえましょう。

たずねているのは　あめだま　の　かず　です。

人数（にんずう）は、たずねてない　のです。

なので、あめだまの　あわせた　かず　を　もとめるためには、　「しき」　も、　あめだま　だけ　計算すればいいのです。

男の子のあめだま　は　７こ

女の子のあめだま　は　５こ

なので　しき　は

７＋５

で、計算すると

７＋５＝１２

です。

なので、こたえは、　１２こ　です。

おぼえてほしい　こと

もんだい　を　出されたら、「なにを　たずねているのか」　を、しっかりと、よんでください。

そして、もんだいが　たずねていることに、　こたえてください。

さんすうドリル

今（いま）までに　ならった　ちしき　を　つかって　、もんだい　を　もっと　たくさん　ときたい　人（ひと）　は　、
「2ねんせい の ため の さんすうドリル」　の　ページ　を　見（み）に 行って（いって） ください。

下（した）　の　「2ねんせい の ため の さんすうドリル」の　文字（もじ） を　おすと、
見ている（みている） ページが ドリルのぺージに かわります。

• 2ねんせい の ため の さんすうドリル