小学校算数/3学年
0をかけるかけ算
[編集]かけ算は数字に0をかけることも、また0に数字をかけることもできます。たとえば、
- 1つ10円の おかし を 0こ 買いました。 お店に はらう お金 は いくらに なりますか。
式(しき)は、となりますが、もんだいをよく見ると おかしは1つも買っていません。 もちろん お店にはらうお金は ありません。答えは、0円に なります。
式(しき)を書くと、
- 10×0 = 0
です。
また、それが5円のおかしでも 100円のおかしでも 買わなければ 店にお金を はらわなくていいことに なります。 このように どのような数でも 0をかけると 答えは0 になります。
- 5×0 = 0
や
- 100×0 = 0
などです。
また、次のもんだいも見てみましょう。
- 0本の えんぴつが入っているふでばこが 7こあります。えんぴつは ぜんぶで 何本ありますか?
式は、 となりますが、 7このふでばこには どれにも えんぴつは1本も入っていません。 もちろん えんぴつは ふでばこには ありません。 答えは、0本 に なります。
- 0×7 = 0
です。
また、ふでばこ が 3こ あっても 20こ あっても 中に 何も入っていなければ、えんぴつ は ない ことになります。このように 0にどんな数をかけても、答えは 0 に なります。
式(しき)を書くと、
- 0×3 = 0
や
- 0×20 = 0
などです。
さいごに、 は どうなるでしょう。 何もないもの に べつの何もないもの を かけても かわり は ありませんね。 の 答えも 0 に なります。
わり算
[編集]わり
- いちごが、20こ あります。このいちごを、4人におなじ数ずつ分けます。一人分は何こになりますか。
- いちごが、20こ あります。このいちごを、4こずつ分けようと思います。何人に分けられますか。
などの問題を考えるときに使います。
式は、
と、なります。 「にじゅう わる よん は ご」と読みます。
は 「わる」 と読みます。
このとき、20を、 「わられる数」 といい、4を 「わる数」 と いいます。
式に あらわす ときは、
- (わられる数) ÷ (わる数)
と、なるように します。
このような計算を、 わり算 といいます。
わり算の 答えのもとめかた
[編集]例えば、
- 18本のえんぴつを6人におなじ数ずつ分けようと思います。1人分は何本になりますか?
(1人分の数)×6 が、18本 ですね。1人分の数は、 ☆×6=18 のあてはまる数と同じなのです。何に6をかけると、18になるかを計算すると、1人分のえんぴつの数がわかります。そのため、 です。
あまりのある わり算
[編集]例えば、
- 23まいのおり紙を4人におなじ数ずつ分けようと思います。1人分は何まいになりますか?
さきほどと同じように計算しましょう。 1人分の数×4 が23本です。あてはまる数 を さがしてみましょう。かけ算の 4 の だん を さがして 、 … しかし、どうしても23にはなりません。 に をたすと→ に なりました。
ですから、このような時は あまり というようにします。「あまり」とは、分けたあとののこりのことです。あまりは、わる数より小さくしなければいけません。たとえば、 あまり (わる数4はあまり7より大きい)としてはいけません。
0をわる わり算
[編集]次のもんだいを考えてみましょう。
- 0こ のおはじきを 5人で おなじ数ずつ 分けました。 1人分は 何こ に なりますか?
式は となりますが、分けられるおはじきは 1つも ありません。 ですから、もらえる おはじき も ありません。答えは、0こ に なります。 また、2人で 分けても 10人で 分けても おはじきが なければ もらうことは できません。 このように 0を ほかの数字(0はのぞきます。次の「0でわるわり算」を見てください)でわっても答えは0になります。
0でわるわり算
[編集]次の もんだいを 考えてみましょう。
- 10こ の おはじきを 0人で おなじ数ずつ 分けました。 1人分は 何こ に なりますか?
式は になりますが、おはじきを もらう人が 1人も いないのに 1人分は何こと もんだい では きいています。 こう書けば もんだい じたい が おかしいことが 分かります。 このようにある数字を 0 で わることは できません。
最後に、 を考えてみましょう。これもわる数が0なので 計算することはできません。
たし算とひき算の筆算
[編集]かけ算の筆算
[編集]かけ算も、
たとえば 13×8 を筆算で計算すると、
| 1 | 3 | |||||
| × | 8 | |||||
| 2 | 4 | |||||
まず、一のくらいどうしをかけます。
- 3×8=24
です。
24の、くりあがりは「2」です。この2は小さく書いて 24 と書きます。
| 1 | 3 | |||||
| × | 8 | |||||
| 82 | 4 | |||||
つぎに、かけられる数 の 十のくらいの数と、かける数 の 一のくらいの数 を かけます。
- 1×8
です。
これは、10×8を
| 1 | 3 | |||||
| × | 8 | |||||
| 82 | 4 | |||||
| 1 | 0 | 4 |
一のくらいを、そのまま下に、おろします。
つづけて、十のくらいどうしを、足し算して(この場合は 2+8=10)、下に おろします。
べつの数の かけ算 でも、ためしてみましょう。
- 24×17
こんどは、2けたの数 どうしの かけざん です。
| 2 | 4 | |||||
| × | 1 | 7 | ||||
| 2 | 8 | |||||
かけ算のひっさんでは、まず、一のくらいどうしを、かけ算します。
このばあい 4×7 = 28 です。 くりあがりの2は、ちいさく書くので、 28 のように書きます。
| 2 | 4 | |||||
| × | 1 | 7 | ||||
| 1 | 42 | 8 | ||||
つぎに、かけられる数の十のくらいの数と、かける数の一のくらいの数を、かけます。
- 24×17
のばあい、 2×7 です。
これは20×7を、
ですから、この 2×7 =14 の意味は 20×7 = 140 ですから、
2×7=14の、こたえの14の、1を百のくらいに書いて、4を十のくらいに書きます。
| 2 | 4 | |||||
| × | 1 | 7 | ||||
| 1 | 42 | 8 | ||||
| 4 | ||||||
つぎに、かけられる数の一のくらいの数と、かける数の十のくらいの数を、かけます。
- 24×17
のばあい、 4×1 です。
これは 4×10 を、
ですから、この 4×1 =4の意味は 4×10 = 40 ですから、
4×1 =4 の、こたえの4を十のくらいに書きます。
| 2 | 4 | |||||
| × | 1 | 7 | ||||
| 1 | 42 | 8 | ||||
| 2 | 4 | |||||
つぎに、かけられる数の十の位の数と、かける数の十の位の数をかけます。
- 24×17
のばあい、 2×1 です。
これは 20×10 を、
なので、この 2×1 =2 の意味は 20×10 = 200 ですから、
2×1 =2 の、こたえの2を 百のくらい に書きます。
| 2 | 4 | |||||
| × | 1 | 7 | ||||
| 1 | 42 | 8 | ||||
| 2 | 4 | |||||
| 8 |
一のくらいを おろします。
| 2 | 4 | |||||
| × | 1 | 7 | ||||
| 11 | 42 | 8 | ||||
| 2 | 4 | |||||
| 0 | 8 |
十のくらいの 2と4と4を 足しあわせて、2+4+4=10を、おろします。
くりあがりの1は、たしざんのひっさんのように、たす前の数の上に、かいておきます。
148 の 1 の上に、くりあがりがついて、1148 に、なっています。
| 2 | 4 | |||||
| × | 1 | 7 | ||||
| 11 | 42 | 8 | ||||
| 2 | 4 | |||||
| 4 | 0 | 8 |
それから、百のくらいどうしを、足します。
- 1+1+2=4
です。
24×17 の こたえ は 408 です。
こうして、かけざん の ひっさん で、かけざん の こたえ が もとめられました。
- ひっさん の しくみ
しくみは このようになっています。
- 24×17 =(20+4)×(10+7)
- = (20+4)×10 + (20+4)×7
- = (20×10) + (4×10) + (20+4)×7
- = (20×10) + (4×10) + (20×7) + (4×7)
これが、この 24×17 の ひっさん の しくみ です。
- れんしゅう
12×12 =
31×70 =
65×45 =
31+70 =
85×74 =
63-44 =
69×45 =
67×54 =
- こたえ
10×6 = 60
12×12 = 144
31×70 = 2170
65×45 = 2925
31+70 = 101
85×74 = 6290
63-44 = 19
69×45 = 3105
67×54 =
さいご の 、67×54 の こたえ は ここでは おしえません。ちゃんとといてから、こたえをしらべてください。
一億までの数
[編集]10000 のことを
一万に一万をたしあわせた数を 二万 といい、20000 とかきます。つまり、1万を2
おなじように、一万を3倍した数は 三万 といい、30000 とかきます。
- また、一万を10倍した数を 十万 といい、100000 とかきます。
- 十万を10倍した数を 百万 といい、1000000 とかきます。
- 百万を10倍した数を 千万 といい、10000000 とかきます。
- 千万を10倍した数を
一億 といい、100000000 とかきます。 次 の数を読んでみましょう。
- 13515271(
東京都 の人口)
- 答えは 千三百五十一万 五千二百七十一 です。
| 一億の くらい |
千万の くらい |
百万の くらい |
十万の くらい |
万の くらい |
千の くらい |
百の くらい |
十の くらい |
一の くらい |
|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 5 | 1 | 5 | 2 | 7 | 1 |
二十万は 200000 だと、0が多くて よみづらいので、「20万」というふうに、数字と
おなじように、三十万なら、30万と かくことも、あります。
64000000 のように、0が多いと、よみづらいので、「6400万」と かくことも あります。「6400万」なら「ろくせんよんひゃくまん」と よみます。
大きな数でも、いままでと おなじように 計算できます。
たとえば、東京都の人口 13515271 人と、
13515721- 7338536 = 6176735 より、6176735人です。
問題
タカシくんのお父さんが、つとめ先の会社からもらう きゅうりょう は、 1か月あたり、300000円(30万円) でした。
1年間で12回、おなじ金がくの給料を、お父さんは、会社から、うけとっています。
1年間で、タカシくんのお父さんは、会社から何円、給料(きゅうりょう)を もらうでしょうか?
- (※ ぜい金などは考えません。)
しき 300000 × 12 = 3600000
タカシくんのお父さんは、一年で360万円、きゅうりょうをもらっていることになります。
こたえ
- 360万円
- (「3600000円」と書いてもいい。)
長さ
[編集]道のりを
時こくと時間
[編集]時こくと 時間 に ついて 学びましょう。
たかしくんは、3時50分に家を出て、4時15分に
3時50分から4時までは10分で、4時から4時15分までは15分です。だから、10+15=25分となります。
秒
[編集]「
10倍、100倍、1000倍、10でわった数
[編集]250を10
図形
[編集]円と球
[編集]
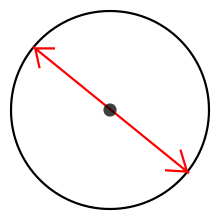

コンパスでかけるまるい形を、 円 といいます。円は、コンパスで書くことができます。コンパスでの円の書き方も
円の


ドッジボール や サッカーボール のような まるいボール を ま上 や ま
ボールは、どこから見ても円に見えます。
ボールのように、どこから見ても円に見える立体を
円は、球ではありません。円は立体ではありませんが、球は立体です。 じゃがいもの形は 円ではありません。じゃがいもは 球でもありません。
-
野球のボール
-
バスケットボール
-
テニスのボール
-
ソフトボール用ボール
-
じゃがいも
角
[編集]2本の
三角形
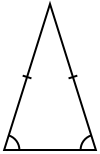
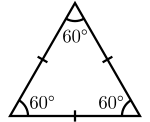
[編集]下の図のように、2辺の長さが
下の図のように、3辺の長さが 等しい 三角形 のこと を
分数
[編集]1mのテープがあります。これを3
- 1mを3等分したうちの2つの長さを 「m」とかき「3分の2メートル」とよみます。mの2こ分です。
,のような数を
(
(答え)は2こ、は4こ
は1のことです。 =1
小数
[編集]1mのを0.1m, 1mのを0.2m…と
この0.1や1.3のように、位(くらい)に 1よりも小さい数を ふくんだ数を 「.」をつかって、あらわした数を 小数(しょうすう) といいます。 また、この点「.」のことを 小数点(しょうすうてん)といいます。
0,1,2…のような数(かず)を 整数(せいすう) といいます。
- れい
- 0.4cm は 4mm の、ことです。
- 0.8L (0.8リットル)は 8dL のことです。
- 2.9cm は 29mm のことです。
- 8.3L は 83dL のことです。
- 8.0L は 8L のことです。
- 7.0L は 7L のことです。
- 7.0cm は 7cm のことです。
- 7.0cm は 70mm でも、あります。
- 4.0cm は 4cm です。
- 4.0cm は 40mm でも、あります。
1cm は 10mm ですね。1mm は 0.1cm です。
100cm は 1m ですね。1cm は 0.01m です。
1L は 10dL ですね。1dL は 0.1L です。
小数の計算
[編集]3デシリットルに5デシリットルを足せば(たせば)、8デシリットルです。
- 3+5=8
ですね。
3デシリットルを0.3リットルとかんがえて、おなじように5デシリットルを0.5リットルと考えましょう。
- 0.3 + 0.5 =
こたえは、いくつでしょうか。
こたえの8デシリットルは 0.8 リットルとも、書けますね。
0.3リットル に 0.5リットル を足しあわせて、あわせて 0.8リットル に なるわけですから、
式は、
- 0.3 + 0.5 = 0.8
と、式は、なります。読みかたは「れいてんさん たす れいてんご は(わ) れいてんはち」と読みます。
- 例(れい)
- 0.4dL に 0.2dL をたすと、あわせて 0.6dL に なります。
- 2.4dL に 0.2dL をたすと、あわせて 2.6dL に なります。
- 2.4L に 0.6L をたすと、あわせて 3L に なります。
- 2.4dL に 0.6dL をたすと、あわせて 3dL に なります。
- 2.4cm に 0.6cm をたすと、あわせて 3cm に なります。
- 2.4 に 0.6 をたすと、あわせて 3.0 に なります。
つまり
- 2.4 + 0.6 = 3.0 = 3
です。
- 7.1cm に 2.6cm をたすと、あわせて 9.7cm に なります。
- 7.1mm に 2.6mm をたすと、あわせて 9.7mm に なります。
- 7.1m に 2.6m をたすと、あわせて 9.7m に なります。
- 7.1 に 2.6 をたすと、あわせて 9.7 に なります。
つまり
- 7.1 + 2.6 = 9.7
です。
小数の引き算
[編集]4リットル から 3デシリットル を、へらしたら、こたえは 37デシリットル ですよね。
単位(たんい)を、すべてリットルにかえると、
4リットル から 0.3リットル をへらして、こたえが 3.7 リットル に なったわけです。
式で書くと、
- 4 ー 0.3 = 3.7
です。読み方は、「よん ひく れいてんさん は さんてんなな」と読みます。
べつの数にしてみて、メートルでも、かんがえてみましょう。
0.8m から 0.2mを、へらしたら、こたえは 0.6m ですね。
式で書くと、
- 0.8 ー 0.2 = 0.6
です。読み方は、「れいてんはち ひく れいてんに は れいてんろく」と読みます。
□を使った式
[編集]式を書くときにわからないことを□で
等号と不等号
[編集]のように、
表とグラフ
[編集]表
[編集]表(ひょう)とは、たくさん、ある、なにかの数を、分かりやすくするために、まとめたものです。
たとえば、ウィキ小学校の3年1組のクラスのみんな(41人)に、好き(すき)な虫を、聞いてみると、つぎのような結果になりました。
カブトムシが好きな人が9人、クワガタが好きな人が7人、トンボが好きな人が6人、セミが好きな人が4人、スズムシが好きな人が4人、バッタが好きな人が3人、カマキリが好きな人が2人、 その他の虫が6人です。
これを表にすると、
| 好きな虫 | 人数 |
|---|---|
| カブトムシ | 9 |
| クワガタ | 7 |
| トンボ | 6 |
| セミ | 4 |
| スズムシ | 4 |
| バッタ | 3 |
| カマキリ | 2 |
| そのほか | 6 |
| 合計 | 41 |
という表に、なります。
合計を書くのは、きまりでは、ありません。もし、合計を書く場合は、表のさいごに、合計を書くのがふつうです。
おなじ質問を2組の人に聞いたら、
| 好きな虫 | 人数 |
|---|---|
| カブトムシ | 6 |
| クワガタ | 5 |
| トンボ | 7 |
| セミ | 3 |
| スズムシ | 8 |
| バッタ | 5 |
| カマキリ | 1 |
| そのほか | 5 |
| 合計 | 40 |
だったとします。
1組と2組をあわせて、
| 好きな虫 | 1組 | 2組 |
|---|---|---|
| カブトムシ | 9 | 6 |
| クワガタ | 7 | 5 |
| トンボ | 6 | 7 |
| セミ | 4 | 3 |
| スズムシ | 4 | 8 |
| バッタ | 3 | 5 |
| カマキリ | 2 | 1 |
| そのほか | 6 | 5 |
| 合計 | 41 | 40 |
と、まとめることも、できます。
3年生が3組まであったとして、3年3組にアンケートをした結果、
| 好きな虫 | 人数 |
|---|---|
| カブトムシ | 5 |
| クワガタ | 4 |
| トンボ | 4 |
| セミ | 5 |
| スズムシ | 3 |
| バッタ | 7 |
| カマキリ | 6 |
| そのほか | 7 |
| 合計 | 41 |
の場合、3年生全体は、
| 好きな虫 | 1組 | 2組 | 3組 | 合計 |
|---|---|---|---|---|
| カブトムシ | 9 | 6 | 5 | 20 |
| クワガタ | 7 | 5 | 4 | 16 |
| トンボ | 6 | 7 | 4 | 17 |
| セミ | 4 | 3 | 5 | 12 |
| スズムシ | 4 | 8 | 3 | 15 |
| バッタ | 3 | 5 | 7 | 15 |
| カマキリ | 2 | 1 | 6 | 9 |
| そのほか | 6 | 5 | 5 | 16 |
| 合計 | 41 | 40 | 41 | 122 |
のように、まとめられます。
グラフ
[編集]グラフとは、なにかについての、いくつもの数を、見やすくするために、数を図に おきかえて、図で 数をあらわしたものである。
棒グラフ(ぼうグラフ)は、四角い棒の長さで何らかの数を表したグラフです。
棒を のばす方向は、上下の方向にのばす場合と、または、横にのばす場合があり、とくにどちらかにするかの、きまりはないです。
棒グラフの例として、ウィキペディアの記事「棒グラフ」から記事と表とグラフを引用し、説明する。
- 例
例として、2004年の欧州議会選挙(おうしゅうぎかいせんきょ)の結果と1999年の欧州議会選挙の結果を使う。以下の表は、それぞれの政党(せいとう)が、手にした議席数(ぎせきすう)である。1999年の総議席数(そう ぎせきすう)は少ないので、1.16933倍して、2004年のときと総議席数が同じになるようにしてある。
「選挙とはなにか」を知りたい場合は小学校6学年の教科書の政治・国際編を見てください。
| 政党 | 議席数 (2004) | 議席数 (1999) |
|---|---|---|
| EUL | 39 | 49 |
| PES | 200 | 210 |
| EFA | 42 | 56 |
| EDD | 15 | 19 |
| ELDR | 67 | 60 |
| EPP | 276 | 272 |
| UEN | 27 | 36 |
| その他 | 66 | 29 |
上記の2004年の選挙結果を棒グラフにしたものを、つぎに、しめす。

次の棒グラフは、2004年の結果と1999年の結果を、両方とも、しめしたものである。

のようなグラフになります。
このように、棒グラフをつくるには、あらかじめ表をつくる必要があります。
また、グラフでは、こまかい数字は、わかりません。
表やグラフについて、くわしくは、教科書や参考書、あるいは外部のウェブサイトなどで、しらべてください。
このページでは、説明しきれません。
そろばん
[編集]算数ドリル
[編集]今(いま)までに ならった ちしき を つかって 、もんだい を もっと たくさん ときたい 人(ひと) は 、
「3年生のための算数ドリル」 の ページ を 見(み)に 行って(いって) ください。
下(した) の 「3年生のための算数ドリル」の 文字 を おすと、
見ている ページが ドリルのぺージに かわります。