線型代数学 > 固有値と固有ベクトル
ある線型変換  に対して、
に対して、 のような元
のような元 が見つかれば、この線型変換は扱いやすくなる。このページでは、このような
が見つかれば、この線型変換は扱いやすくなる。このページでは、このような (固有値・固有ベクトル)について議論をする。
(固有値・固有ベクトル)について議論をする。
 せん断写像と言う種類の線形写像でモナリザの絵を変換した。このとき赤のベクトルは方向を変えたが、青のベクトルは変換後も方向を変えていない。この青のベクトルが固有ベクトルである。
せん断写像と言う種類の線形写像でモナリザの絵を変換した。このとき赤のベクトルは方向を変えたが、青のベクトルは変換後も方向を変えていない。この青のベクトルが固有ベクトルである。
注意
ここから先の議論は全て複素数体  上の議論である。
上の議論である。
本題に入る前にまず次の定理を認めてもらいたい。
定理(代数学の基本定理)
複素数係数の任意のn次多項式

は重複度も含めてn個の複素数の根を持つ。
証明は複素解析学#リウヴィルの定理を参照のこと。
まず、このページの初めに書いたことを正確に定義しよう。
定義
 上の線型空間、
上の線型空間、 とする。
とする。
このとき、 が
が

の関係をみたすとき、 を固有値 (eigen value)、
を固有値 (eigen value)、 を固有ベクトル (eigen vector)という。
を固有ベクトル (eigen vector)という。
では、どのようにして固有値や固有ベクトルを求めたらよいだろうか?
まずは、 の線型変換である行列について考えてみよう。
の線型変換である行列について考えてみよう。
まず、固有多項式を次のように定義する。
定義
 に対して
に対して

を の固有多項式 (eigen polynomial)という。また、
の固有多項式 (eigen polynomial)という。また、 を
を  の重複度 (multiplicity)という。
の重複度 (multiplicity)という。
2番目の等式は代数学の基本定理より成り立つ。
すると、次の定理が成り立つ。
定理
 が固有値
が固有値  は固有多項式の根
は固有多項式の根
(証明)
 に対して、
に対して、 が固有値であるとする。このとき、
が固有値であるとする。このとき、

をみたす、 が存在する。
が存在する。
上の式を書き直すと、  であるから、
であるから、 の階数がnより小さいということと同値である。
の階数がnより小さいということと同値である。
つまり、 でなければならない。
でなければならない。
以上をまとめると、
 が固有値
が固有値  が非自明な解をもつ。
が非自明な解をもつ。  □
□
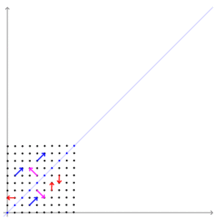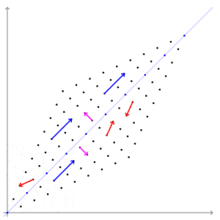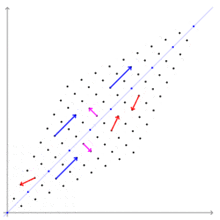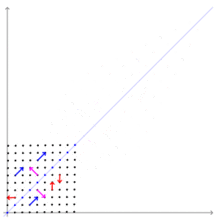 行列
行列 によって引き起こされる線形変換。
によって引き起こされる線形変換。
行列 の固有値と固有ベクトルを求める。右の図はこの行列によって引き起こされる変換を示している。この行列
の固有値と固有ベクトルを求める。右の図はこの行列によって引き起こされる変換を示している。この行列 の固有値と固有ベクトルを求める。
の固有値と固有ベクトルを求める。

なので、方程式 を解いて、行列
を解いて、行列 の固有値は1と3である。
の固有値は1と3である。
次に固有ベクトルを求める。固有ベクトルを求めるには、 を満たすベクトル
を満たすベクトル を求めれば良い。
を求めれば良い。
 に対応する固有ベクトルは、
に対応する固有ベクトルは、 であることから、
であることから、 を満たすベクトルである。すなわち、固有ベクトルは
を満たすベクトルである。すなわち、固有ベクトルは 及び、これを任意の定数倍したものである。
及び、これを任意の定数倍したものである。
 に対応する固有ベクトルは、
に対応する固有ベクトルは、 であることから、
であることから、 を満たすベクトルである。すなわち、固有ベクトルは
を満たすベクトルである。すなわち、固有ベクトルは 及び、これを任意の定数倍したものである。
及び、これを任意の定数倍したものである。
右の図では、紫のベクトルは、固有値1に対応する固有ベクトル に平行なベクトルである。青のベクトルは、固有値3に対応する固有ベクトル
に平行なベクトルである。青のベクトルは、固有値3に対応する固有ベクトル に平行なベクトルである。紫のベクトルは、変換された後も、方向は変らず、長さも変わっていない。青のベクトルは、変換された後も、方向は変らず、長さは3倍になっている。固有ベクトルではない赤のベクトルは、変換された後、方向を変えている。
に平行なベクトルである。紫のベクトルは、変換された後も、方向は変らず、長さも変わっていない。青のベクトルは、変換された後も、方向は変らず、長さは3倍になっている。固有ベクトルではない赤のベクトルは、変換された後、方向を変えている。
次に、固有空間を以下のように定義する。
定義
 の
の に対する固有空間 (eigen space)とは
に対する固有空間 (eigen space)とは

で表わされる部分空間のことである。
この定義から明らかなように、
 が固有値
が固有値  は
は でない元を持ち、それらはすべて固有ベクトル
でない元を持ち、それらはすべて固有ベクトル
である。
 上の線型空間、
上の線型空間、 を
を の基底、
の基底、 に対して
に対して  は固有値であるとする。
は固有値であるとする。
また、 に対する
に対する  の表現行列を
の表現行列を  とする。
とする。
このとき、行列の場合と同様に、

を充たす が存在する。
が存在する。 の恒等変換(identity transformation)を
の恒等変換(identity transformation)を  とすると、
とすると、

と変形できる。これは、 と同値である。
と同値である。 の表現行列は
の表現行列は  であるから、
であるから、 
以上より、 の固有値は
の固有値は の固有多項式の根であることがわかる。
の固有多項式の根であることがわかる。
また、正則行列 に対して
に対して

より、固有多項式は の基底の取り方によらない。
の基底の取り方によらない。
固有空間も行列の場合と同様に定義される。
定義
 の
の に対する固有空間とは
に対する固有空間とは

で表わされる部分空間のことである。
最後に、次の命題を証明しておく。
命題
 は
は  の相異なる固有値とする。このとき、
の相異なる固有値とする。このとき、

(証明)
 は
は  をみたすとする。
をみたすとする。
この等式に、 を作用させると、
を作用させると、

左辺の行列の行列式はVanDermondの行列式なので、

したがって、この行列は正則。
よって、 □
□





































































