高等学校物理/物理I/波/音波と振動
音
[編集]うなり
[編集]振動数の少しだけ違う2つの おんさ(音叉) を鳴らすと、周期的に音が大きくなったり小さくなったりするのが聞こえる。
なお実験で音叉(おんさ)を準備するにあたって、音叉に おもり をつけると振動数が下がるので、軽い おもり を音叉の先端のほうにつける事で、振動数の少しだけ低い おんさ を作れるので、実験の際の参考に。
この現象を "うなり"(beat) という。この時、音の大きさが変化する周波数は2つの波の振動数の差に等しい。 つまり、 うなりの周波数を f[Hz] とすると、もとの2つの音叉の振動数をそれぞれ f1[Hz] および f2[Hz] とすると、
である。
こうなるわけを理論的に考えると、うなりの周期を T[s] とすると、時間Tの間には 振動数 f1 の音叉は f1T 回の振動をして、同じ時間 T の間に 振動数 f2 の音叉は f2T 回の振動をする。
そして、音叉を鳴らしてからT秒後に始めて、時刻0の時と同じ波形を繰り返すことになるはずだが、そのためにはf1音叉とf2音叉の波の数が1個だけ違えば良い。 なので、
である。
両辺を T で割れば、
だが、うなりの振動数を f とすれば、振動数と周期の公式により
であるので、 つまり
これを整理して、
- (証明おわり)
- 発展: 音波の三角関数による近似と、その限界
「うなり」を計算する際、ひとつひとつの音叉(おんさ) をたたく事によって発生する(それぞれの音叉からの)音の強さを、数式であらわすとき、高校レベル 〜 大学入試レベル では、(音叉をたたく事によって発生する音の縦波としての式は)「ひとつの振動数だけで、なりたっている」と近似して良い。
また、そのため、音叉をたたく事によって発生する音の強さの式は、数学の「三角関数」をもちいて近似できる。もちろん、その音波を近似した三角関数の振動数の値は、音の振動数と同じ値である。(なお、音は縦波であるので、けっして波の形状は三角関数ではない(というか、そもそも、(水面波のような)形状は音波には無い)。音の計算の際に、三角関数で近似的に記述される対象は、音を構成している個々の空気のかたまりの移動方向である。一般に、縦波を三角関数であらわす公式で記述される対象は、その縦波を構成する媒体の、個々の位置での移動方向である。)
もっとも、三角関数で近似できると言っても、ひとつの音叉の音だけでは、まったく、音の強さが周期的に変化する様子は、聞こえない。(※ 耳の構造なども関係する話題なので、あまり深く考える必要は無い。)
なので、音の計算で三角関数が役立つのは、あくまで「うなり」を計算するような場合だけであろう。
- (※ 高校必修の範囲外だが、下記の発展項目のように、音としての(空気の)振動・波動を三角関数で近似できると仮定すると、そこから「うなり」の起きる現象を式変形で導出できる。)
なお実際には、音叉から出てくる音の大きさは、しだいに減衰していくこともあり、実際には音は三角関数どおりの強さではない。しかし高校では、そこまで考えなくても良い。音叉をたたいてから数秒ていどの期間の音の強さなら、三角関数で近似しても、かまわない だろう。
大学入試の問題などでも、音のうなりの計算などの際に、音を三角関数で近似する事によって解く問題が、出題される事も多い。
ただし、この三角関数による波形の近似は、あくまで近似による単純化である。現実の音波の波形は、もっと複雑である。
なお、人間の声の音波や、動物の鳴き声などの音波の近似は、けっして音叉のようには、単純には近似できない。もちろん、録音機などで人間の声などが録音できるように、生物の声などを数学的に取りあつかう技術や数学理論もあるのだが(「フーリエ解析」など)、しかし高校レベルを大幅に超える技術なので、説明を省略する。
- 発展: うなりの計算
もし読者が、「三角関数」の「和積・積和の公式」および、「三角関数」の「加法定理」を知っていれば、音波を三角関数で近似して、その三角関数の計算によってうなりの公式を証明する事もできる。
- ※ 詳しい解説は、下記の計算式を参照。かなり計算が難しいので、高校1年の人や、始めてこの単元を学習する高校2年生の人は、この発展の項目(三角関数による、うなりの公式の導出)を飛ばして良い。
うなりの計算は三角関数の計算に帰着する。この時、波の振幅の式が振動数が2つの波の振動数の差となる三角関数となれば良い。
まず、2つの波を および とおく。
ここで、はそれぞれ2つの波の位相差、片方の波の角振動数、2つの波の角振動数の差、各波の振幅に対応する。
2つを足しあわせて、三角関数の加法定理(高等学校数学II)などを用いると、
となる。ただし、は条件を満たす位相である。
最後の式は、ルートの中の部分が振幅であり、つまりルートの中の部分が音の大きさである。このルートの中の部分に、tを変数とする三角関数が入っているため、そのルート中の三角関数の振動数こそが、うなりの振動数である。
これらの計算結果から導ける事とは何かというと、次のことであろう。
- 「音叉を叩いて得られる音の波形は、正弦波にちかい事が分かる。」
このような事が、導けるだろう。
なぜなら、音波を正弦波と仮定して、「うなり」の式を導出し、それが実験結果を説明できるのだから。(物理学とはそもそも、実験結果を、より少数の法則から説明するための学問である。)
実験結果を説明できる仮定は、もし特に反例が(さまざまな実験をしても)見つからなければ、その仮定は物理学では充分に「正しい」仮定である。
そして、我々が この計算にあたって、設定した「仮定」とは、「音叉を叩いて得られる音の波形は、正弦波である。」という仮定であった。
よって、音叉を叩いて得られる波形のかたちは、正弦波に近いかたち である事が、実験と計算により導出された。
(※ 範囲外: )このほか、音波がたしかに波であることの根拠となる実験的事実としては、音速の実測値が、音を波だと仮定した場合の波動方程式の解から得られる理論値に近いこともまた、音が波であるという理論を補強する。
弦の振動
[編集]
ギターの弦などのように、両端を固定した弦を考える。両端を固定した弦をはじいて振動させると、両端で波が反射するので、最終的に定在波が出来る。なお、この波は横波である。この定在波の波長については、両端が固定されているので、波長には図のような条件がある。
両端で、定在波が節(ふし)にならなければならないという条件である。
節から節までの長さは、半波長 なので、 両端間の距離 l が、半波長の整数倍にならなければならない。
これを式でかくと、「整数倍」の整数をmとすれば、
- (m=1,2,3,・・・)
波長が未知数なので、波長について求めるために移項して
- (m=1,2,3,・・・)
となる。
波長に、このような両端間の長さによる条件があるので、振動数にも同様に両端間の長さによる条件がつく事になる。弦を伝わる波の速度を v[m/s]として、振動数 f[Hz] の条件を求めると、
である。
m=1のときの固有振動を基本振動(きほん しんどう)といい、そのときの振動数を基本振動数という。また、基本振動のときに生じる音を基本音(きほんおん)という。
m=2、3、・・・のような基本音以外の音を倍音(ばいおん)という。
m=2のときの音を2倍音といい、m=3のときの音を3倍音という。m=4以上でも同様。
弦を弾いたときに出る、じっさいの音では、基本音のほかにも、倍音が混在している。つまり、基本振動のほかにも、倍振動が、混在している。
だが、生じる音のなかで、全体的には基本音が大きいので、音の高さは基本音によって決まる。(検定教科書でも、基本音で音の高さが決まる、と主張してある。)
- 線密度
であったが、上式での弦を伝わる横波の速度 v[m/s] については、弦を引く張力 S[N] と、弦の質量の線密度 ρ[kg/m] という、2つの量によってのみ決まる定数である。
弦で、単位長さあたりの質量のことを、線密度(せんみつど)という。
弦が軽いほど弦が動きやすくなり、その結果、波が伝わるのが早くなる。
また、張力が強いほど、弦をもとに戻そうとする力が大きいので、その結果、波が伝わるのが早くなる。
この弦を伝わる波の速度の式の導出については、大学レベルの偏微分の知識が必要なので、証明を省略する。また、高校生は、この弦の波の速度の式を覚えなくて良い。(ふつうの入試などでは、この公式は、出題時に問題文で用意されるはずである。)
さて、このように、弦の振動数
は、 両端間の長さによって制限されて固有なので、このような弦の定在波の振動を固有振動(こゆうしんどう)という。
また、このような弦の定在波の振動における周波数を固有周波数(こゆう しゅうはすう)という。 固有振動のうち、m=1 のものを基本振動という。 m=2 のものを 2倍振動 という。m=3 のものを 3倍振動 という。
- ※ 学生は覚えなくてもいいです。
バイオリンのように弦をこすって振動させる場合の現象は、上記とは、違う。19世紀にすでに物理学者ヘルムホルツがバイオリンの弦の振動について研究している。
本文で説明した例の弦の振動は、ギターや琴などのような、弦をはじいたあとに、弦から手を離す装置の場合。つまり、高校で習う 弦の振動 は、ギターのような弦の振動。
気柱の振動
[編集]気柱の振動
[編集]
瓶や試験管に吹くと、音が出る。
これは、気柱が振動しているからである。
瓶や試験管の底では、気柱が軸方向に振動できないので、底で固定端反射が起こる。
一端の閉じた管を、閉管(へいかん)という。両端の開いている管を開管(かいかん)という。
閉管の場合
[編集]閉管の長さをL[m]とすると、図のように、 の奇数倍になる。
音の速さをV[m/s]、固有振動の波長をλm[m]、固有振動数をfm[Hz]、とすれば、
- ( ただし、m=1,3,5,・・・ )
- ( m=1,3,5,・・・ )
となる。
ここで は閉管の基本振動数である。
開管の場合
[編集]
開管では、両端が、腹の位置になる。
波長の式は、
- ( ただし、m=1,2,3,・・・ )
- ( m=1,3,5,・・・ )
となる。
ここで は開管の基本振動数である。
開口端補正
[編集]
図のように、開口端の腹の位置は、管口よりも、すこし外側に出ている。よって、波長の長さを計算するさい、このぶんの長さを考慮しなければならない。この、管口から腹が出たぶんの長さを開口端補正(かいこうたん ほせい)という。
共振と共鳴
[編集]
固有振動数の等しいおんさを2つ用意して、片方を叩くと、もう一方のおんさに空気の振動が伝わっていき、もう片方のおんさは叩かなくても、振動する。
これが共鳴(きょうめい)または共振(きょうしん)である。
いっぽう、もし、固有振動数のちがうおんさ2つで、片方を叩いても、もう一方のおんさは、あまり振動しない。
- 振り子の共振
- タコマ橋
ドップラー効果
[編集]
波源や観測者が動くと、振動数が変化する現象が見られる。これを、ドップラー効果(Doppler effect)という。
以下、波の速さをV[m/s]、波の振動数をf[Hz]、波源の速さをvs[m/s]、観測者の速さをvo[m/s]、観測される振動数をf' [Hz]として考える。
まず、静止している観測者に波源が近づく場合を考える。 時刻0[s]には波源も波も0[m]の位置にある。 時刻T[s]になると、波はVT[m]、波源はvsT[m]の位置に来る。 ここで、波源から波の到達点までの距離はVT-vsT[m]である。 この距離を時間T[s]で割ると、V-vs[m/s]になるが、観測者はこの速さを波の速さと観測する。 すると、観測される波長λ' [m]は であり、 となる。
- スピードガン
プロ野球でピッチャーの投げるボールの速度を測定したりするのに、ドップラー効果を利用した「スピードガン」という装置が用いられている。
これは、ボールに超音波または電波を当てて、ボールが動いているので、ボールが反射する振動数が、静止してるときとは違う。
ボールから反射して、測定器に戻って来る振動数は、ボールがドップラー効果で音源が運動するときの振動数である。
音の伝わり方
[編集]音はどの方向にも、おおよそ同じ速さで伝わる。 音の速さは有限であり、速度は常温付近では気温[℃]にほぼ比例しておりで表される。15℃の時はおよそ、340[m/s]である。
音の干渉
[編集]空気中の音については、通常は重ね合わせの原理が成り立つ。このことを用いて波の重ね合わせの様子を調べてみる。
- 実験
2つの同じ振動数の正弦波を用意し、位相の差がの奇数倍の場合との偶数倍の場合を観察してみよ。実際には各音源からの距離の差が、の奇数倍と偶数倍に対応する。
この場合距離の差がの奇数倍の時には、音の大きさは2倍になり、偶数倍の時には音はほとんど聞こえなくなるはずである。これは同じ形の波が符号が同じで足された場合と、符号が反対で足された場合に対応するからである。
光
[編集]光の伝わり方
[編集]光も音と同様、ある一点から光を出すとあらゆる方向に同じ速度ですすむ。 光はある一方から入射した場合、直進する。 実際には音も同じ性質を持っており、音を上手くスリットなどで分離すると直進することが知られている。 光の速度は極めて速いが有限であり、その速さは、 2.99792458 × 108 [m/s] である。
光の回折と干渉
[編集]光はせまいスリットを通すと、広がって行くように伝搬することがある。これを回折(かいせつ、diffraction)と呼ぶ。
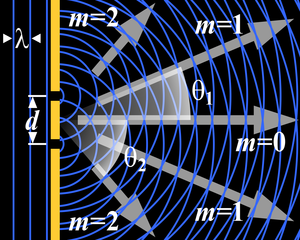
また、光はスリットを上手く使うことで、強めあったり弱めあったりすることがある。 (:ヤングの実験?)
光は実際には空間の中を伝搬する波動である。波動には振動数があるが、振動数によって光の色が変わることが分かる。
- (プリズムの説明?)

振動数が低いものから光の色は赤から紫へと変わって行く。これ以上に振動数が大きくなると、光は人間の目には見えなくなる。このように振動数が可視領域より高くなった光のことを紫外線(しがいせん、ultraviolet)と呼ぶ。
さらに振動数が高いものをX線(エックスせん、X-ray)、 γ線(ガンマせん、Gamma ray)と呼ぶ。いっぽう、赤い光よりもさらに振動数が少ない光も、また同様に、人間の目では見ることが出来ない。このような可視領域よりも振動数の低い光を赤外線(せきがいせん、infrared)と呼ぶ。
追記:光を波と考える方法が一般的に取られているが、多くの現象を説明できるが、例えば光のエネルギーの保存則を説明できない。 海外に於いては2000年頃から高校の教科書の光の説明では、素粒子として説明し、光の干渉など波としての考えを捨てるように書かれている。
※ 範囲外: エネルギーと波
[編集]総論
[編集]波のなかには、波そのものがエネルギーを持つものがある。
少なくとも光と音と水面波は、波そのものがエネルギーを持っており、そのため、効率の大小はともかく、媒体を通じて、波のあたったものにエネルギーを伝えることができる。
たとえば、音は、音のあたった物体をこまかく振動させる。振動にはエネルギーが必要なので、つまり、音がエネルギーを伝えていることが分かる。
光も、光の照射された物体をあたためたり、化学反応を促進させたりするので、よってエネルギーを伝えていることが分かる。
水面波も、水面に浮かんでいる物体を上下に振動させているのが、元の位置より高い時はエネルギーは増加、低い時はエネルギーが減少となり、差し引きゼロで、位置エネルギーは変化してない。
よって、水面波もとりあえずエネルギーをつたえることができる、と見なすのが、妥当だろう。
なお、弦の「振動」については、波ではなく振動であるので、いったん考察を除外する。検定教科書でも、バネにつながれた単振動する おもり に運動エネルギーがあることを習うように、振動には当然、エネルギーがある。
音とエネルギー
[編集]読者は、きっと、小学校の音楽の授業などで、合唱の声による音の振動によって、タイコの膜が小きざみに震えてたりするのを見たこともあるだろう。
さて、物体が振動するということは、エネルギーを持っているという事である
タイコの膜だって、物体によって構成されている。
つまり、タイコの振動する膜には、運動エネルギーや位置エネルギーが、蓄えられているからこそ、振動しているのであり、そのエネルギーが空気中に放出されていっている。
また、音そのものにも、エネルギーがある。(「音そのもののエネルギーとは、運動エネルギーか位置エネルギーか?」については、高校生は気にしなくて良いだろう。)
- ※ タイコの膜は、円形状に広がっているが、このような形状の物の振動も、大学では「振動」として扱う。しかし高校生にとっては、その計算方法が、かなり複雑なので、高校生は深入りしなくて良い。 大学生ですら、膜の振動については、あまり理解していない人は多い。(ベッセル関数などの、大学高学年以上のレベルの、高度な数学が必要になる場合がある。)
- ※ 楽器をつくる人の実務では、推測になるが、いちいち高度な方程式を解いているのではなく、おそらく試作品を何種類もつくって、実験によって、「どの試作品が一番、性能が良いか?」というふうに一番よい形をさがし、楽器の各部の寸法を決めているのだろう。それこそ、古代や中世の時代から、世界各国に楽器はある。
なお、「超音波」(ちょうおんぱ)とは、単に、人間の耳では聞こえないだけの、高周波の音波のことである。
よって、超音波にも、エネルギーがある。
超音波モータ
[編集]電気の「電磁誘導の法則」ではなく、音波の振動エネルギーを使って、モータを回すという、超音波モータという機械装置がある。(※ 中学の技術科の教科書で紹介されている。東京書籍の教科書『新しい技術・家庭 技術分野』、平成23年検定版。)
超音波モータは既に実用化されている。 高い周波数の空気の振動を使うモータを超音波モータと呼んでいる。
超音波モータは、電磁波を発生させないという長所がある。医療現場など、電磁波を嫌う場所で、超音波モータは活用されてる。
- (※ 調査中: )なお、超音波モータのエネルギーを伝わり方についての疑問として、はたして波そのものでエネルギーを伝えているのか、それとも、発生源の振動物体の振動エネルギーが接触している物体を経て、目的物体に伝わっているのか、wikibooks編集者が調査中のため、分からない。字面が超音「波」モーターだからといって、波でエネルギーを伝えている原理だろうとは、決め付けてはならないだろう。なので現状では読者は、超音波のエネルギーを伝えている、と早合点してはならない。
なお、機械で高周波の振動を発生させるには、一般に、「圧電素子」(あつでんそし)または「圧電セラミック」[1]という、電圧を加えると伸び縮みするセラミック系の材料を用いる。(※ 東京書籍の高校化学の検定教科書(平成23年 検定版)で、セラミック化合物の実用の一例として圧電素子を紹介している。もっとも、東書の教科書では、ガスコンロの点火源としての圧電素子の応用だが。)
超音波モータにおける高周波振動の発生源としても、圧電素子は用いられている。(※ 参考文献: 文部科学省 著、『高等学校用 工業材料2』、平成6年初版、平成16年1月20日印刷、文部科学省著作教科書、発行所:実教出版株式会社、ほか[2])
圧電素子とは、電気を加えると、伸びたり(または縮んだり)する、材料である。
この圧電素子には、交流電圧を加えると、高い振動数で振動する材料が多い。なので、もし振動数が超音波の周波数と同じくらいなら、交流電圧の加えられた圧電素子から超音波が発生するという仕組みである。 形あるものは共振周波数があり、小さいと高い周波数、大きいと低い周波数になる。圧電素子は薄いので、高い周波数になる。材料の問題では無く、厚さの問題。
- ※ なお、高分子化合物にも圧電性をもつものがある。ポリフッ化ビニリデンという化合物が、そのような圧電性をもつ高分子である。実教出版の高校化学用の資料集によると、医療機器の超音波診断機器には、ポリフッ化ビニリデンがよく使われてるらしい。
釣り糸にも使われ入手容易な事からポリフッ化ビニリデンが使われる。他にも何種類も圧電性樹脂はある。感度が悪くて良いなら、ほぼ全ての樹脂や絶縁体は圧電性がある。例えば氷も僅かに圧電性がある。
なお、ガスコンロの着火素子につかわれてる圧電素子は、無機セラミックス系の材料である。(チャート式化学などで確認。)
- ※ もしプラスチック系の圧電素子を着火部品につかったら、燃えてしまい、事故になる。参考書には、着火部品に無機セラミックス系をつかっている理由は、特に書かれてないが、おそらく前述した理由だろう。つまり、耐熱性の理由である。プラスチックは耐熱性が無い。セラミックスは耐熱性が高い。
着火用にPZT系振動子が使われている理由は、コストが安く、着火の際の力に耐えるからである。プラスティックだと柔く直ぐに破損する。
- ということは、医療現場でわざわざプラスチック系の圧電素子を使っているのには、それなりの理由があるはず。しかし参考書にも、その理由は特に書かれてない。おそらく、MRI(核磁気共鳴診断装置)などとの磁界の都合ですかね?
水面の波とエネルギー
[編集]ひとくちに水面の「波」といっても、じつは何通りかある。
水面に石をなげこんだときの「波」もあれば(いわゆる「波紋」(はもん))、 海で波がザッバーンと波打つときの、あの「波」もある。
このうち、海の波については、大学の教養課程レベルの「波動」の理論の知識が必要になるので、高校生は深入りしなくて良い。
そして、どちらの波にしろ(波紋にしろ、海の波にしろ)、これらの水の波には、エネルギーがある。
海の波が、海面に浮かんだ 浮き輪 などの物体を、水面といっしょに上下左右に振動させたりするように、物体を振動さえるのだから、海の波にもエネルギーがある。
なお、海の波は、例外として津波などの場合をのぞき、普通の波の場合には海面ちかくだけが揺れており、水中は、あまり揺れていない。
光とエネルギー
[編集]光にもエネルギーがあるのだが、しかし高校2年生には、その計算の仕組みを解説できない。
光のエネルギーの計算方法の理解には、最低でも、高校3年の物理IIで習う、電気の知識や、「光電効果」(こうでん こうか)という現象の知識が必要になる。
高校2年のレベルでは、もっと簡単な理解で良く、たとえば「太陽の光で水が蒸発したりするのだから、光にも、熱と同様にエネルギーがある」とか考えるくらいでも、良いだろう。
(※ 範囲外 : )振動とエネルギー
[編集]弦の振動とエネルギー
[編集]弦楽器を考えれば分かるように、弦の振動にもエネルギーがある。
ここで重要な事は、たとえば、
- これから弦をはじいて音を出そうするために弦楽器の弦を指でつまんで引っぱっていて、そのまま引っぱったままにして、まだ指でつまんだままで離さずに静止している時には、
- その弦に、位置エネルギー が蓄えられているという事である。
そして、弦から指を離せば、(あたかもバネの振動のように、)弦のその位置エネルギーが運動エネルギーに移り変わり、そして、また運動エネルギーが位置エネルギーに変わることで、弦は振動を繰り返すのである。
弦の振動エネルギーと位置エネルギーの計算の知識には、大学の高学年レベルの高度な数学(フーリエ解析など)が必要になり、高校レベルを大幅に超えるので、説明を省略する。
音叉や木琴などの振動
[編集]数式では、音叉(おんさ)や、木琴など、ああいう、叩いて音が出る棒状の楽器の振動は、じつは、かなり高度な数学が必要になる。(「エアリーの応力(おうりょく)関数」などの方程式をあつかう「弾性力学」(だんせいりきがく)といわれる、大学院レベルの数学が必要になってしまう場合がある。)
なので、高校生には、正確な計算は無理なので、単に、「音叉の振動も、音が発生するから、弦楽器の振動とかと同様に、エネルギーがある」くらいに単純に考えて良い。
数式上の波や振動には、エネルギーのない場合もある
[編集]単に数式上だけで、三角関数で表記された物理現象の場合、その対象の物理現象には、エネルギーのない場合もある。
物理学や数学の習慣上、三角関数で表記された数式のことを「波動」という事もある。そのような数式上の「波動」の場合、物体を振動させられない現象を「波動」と読んでいる場合もあり、このような「波動」の場合には、物理的な意味での「エネルギー」を持たない場合もある。
(※ 範囲外: )その他の話題
[編集]衝撃波のエネルギー
[編集]
衝撃波(しょうげきは)は、(飛行機などの)物体が、大気中での音速よりも速い速度で移動したときに、発生する現象のひとつであり、性質は、衝撃波の発生により、(その機体にとっての)空気抵抗が急激に上昇し、騒音が急激に大きくなる、などの性質がある。
字面こそ、衝撃「波」とあるが、果たして本当に波か、あまり、ハッキリしていない。
- ※ 衝撃波の計算には、大学の機械工学の高学年レベルの流体力学の知識が必要になるので、高校生は深入りしないで良い。
なお、大気中での音速は秒速で約340m/sである。時速に換算すると、約 1220km/h 〜 1230km/h である。
大気中での音速のことを「マッハ」ともいい、つまり、秒速340m/sを「マッハ1」と言う場合もある。(もし、ある機体の速度が約680m/sなら、その機体の速度は約「マッハ2」 である。)
「マッハ」という用語を用いるなら、「衝撃波」は、マッハが1を超えた物体から発生する現象である。
なお、ソニックブームとは、衝撃波が、周辺に音波として伝わっていく現象のことである。
音による音の打ち消し
[編集]音は重ね合わせの原理が成り立つので、外界の音の逆の位相の音を加えれば、音を打ち消すことができる。 高級車の場合、エンジンの低周波音の逆位相の音をスピーカから出して、騒音を弱くする様にしている。 車内の消音は高い周波数に関しては、空間が広い為無理だが、運転者だけと限定するなら3kHz程度まで可能。 ノイズキャンセリング・ヘッドホンは耳と言う小さな空間なので、比較的高い周波数まで、本来なら入ってくる外部ノイズを消して、音楽のみが聞こえるようにしている。
































