高等学校物理/物理I/運動とエネルギー/仕事とエネルギー
仕事とエネルギー
[編集]物理学でいう「エネルギー」(英:eneregy エナジー)とは、物理学でいう「仕事」(しごと、英:work ワーク)をする能力のことである。より具体的にいうと、エネルギーとは、静止していた他の物体を動かせる能力のことである。
- (なお、「エネルギー」という読みは、ドイツ語での発音に由来する読み方であり、英語では「エナジー」と発音するのが近い。日本では、この物理量のことは「エネルギー」というのが一般的である。)
では、物理学でいう「仕事」とは何か。それを、これから学んでいこう。
仕事
[編集]仕事
[編集]
物体に力をかけたまま力の方向に移動させることを、「物体に仕事をした」などという。 いっぽう、単に力を加えただけで、物体が動かない場合は、「仕事をしていない」のである。
ここでは、図のように、物体に一定の大きさの力 F[N] を加えたとして、その力の方向に s[m] だけ変位したとする。
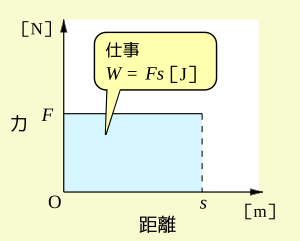
このとき、力がする仕事(しごと、work) W は、つぎの式で表される。
- W=F・s
仕事 Wの単位は ジュール [J] である。 なお
- 1[J]=[N m]
である。
仕事の記号は通常では W または w で書かれる。大文字または小文字のダブリューである。
仕事は、ベクトルではない。
力の向きと変位の向きが異なる場合
[編集]
図のように、水平方向から角度 θ で、力 F で引いている場合で、水平方向に s[m] だけ動かした場合の仕事は、
- W=F・s cos θ
なぜなら、力 F の、移動方向の分力は、
- F cos θ
である。 また、さきほどの節の仕事の定義より、仕事の式の力は、移動方向の分力のみを考えればよい。なお、垂直方向には動いていないので、垂直方向の分力 F・s sin θ は仕事をしていない。なので、水平方向の分力のみを計算すれば仕事が求まる。そして、その、水平方向の分力 F cos θ がする仕事とは、
- W=(F cos θ )・s
である。これを整理して、仕事 W は
- W=F・s cos θ
となる。
負の仕事
[編集]- (未記述)
斜面をすべり降りる場合の仕事
[編集]- (未記述)
仕事の原理
[編集]滑車の場合
[編集]
たとえば図のように動滑車を使うと、物体を持ち上げるのに必要な力は半分になるが、物体を滑車を使わないときと同じ距離だけ持ち上げたい場合に、ひもを持ち上げるのに必要な距離が2倍になるので、結局、滑車を用いても、「力の大きさ × 移動量」という量は同じである。つまり、仕事の大きさは、滑車を使っても変わらない。
てこ や 斜面 でも、力の大きさは変えられても、そのぶん手元の移動距離が増えてしまい、結局、仕事の大きさは変えられない。 仮に摩擦の無い理想的な てこ や 斜面 があったとしても、それを、どんなに組み合わせても、「力の大きさ × 移動量」という量は同じであり、つまり仕事は変わらない。
このように、どんな道具を使って力の大きさを変えても、道具を使わない場合と、仕事が変化しないことを、仕事の原理という。
- (記述中)
てこ の場合
[編集]- (※ ここに図を追加。)
図のように、比率 1:2 の てこ が、あったとしよう。
図で分かるように、距離 h[m] だけ持ち上げるのに必要な力は半分の で済むが、物体を持ち上げるのに必要な手元の移動距離が、2倍の 2h[m] になっている。 結局、仕事は変わらない。
念のため、仕事 W を計算してみても、
であり、結局、距離 h 持ち上げるのに必要な仕事は mgh である。
斜面での仕事
[編集]
図のように、傾き θ の斜面があるとしよう。計算の簡単化のため、斜面は滑らかであるとして、摩擦は無いとしよう。 また、0° < θ < 90° としよう。
この場合、物体を鉛直方向に h[m] だけ高い場所に上げる仕事を計算しよう。
まず、物体を動かすのに必要な力は、斜面を用いた場合、図から分かるように、
である。
しかし、高さhまで上げるために必要な、斜面の距離は、
である。
結局、仕事 W は
となり、仕事は同じである。
※重力加速度などは別である。
運動エネルギーと位置エネルギー
[編集]エネルギー(英:energy エナジー)とは、物理学でいう「仕事」(しごと、英:work ワーク)をする能力の大きさを、数値的に定量的に表したものである。
なお、「エネルギー」という読みは、ドイツ語での発音に由来する読み方であり、英語では「エナジー」と発音するのが近い。日本では、この物理量のことは「エネルギー」というのが一般的である。
運動エネルギー
[編集]運動エネルギー
[編集]運動している物体(仮に、これをAとする。)は、他の物体(仮にBとする。)にぶつかれば、その物体Bに力を及ぼしたり、物体Bを動かしたりできる。
つまり、運動している物体には、仕事をする能力があり、したがって運動している物体はエネルギーを持っている。 この、運動をしている物体が持つエネルギーを運動エネルギー(うんどうエネルギー、kinetic energy)という。
種々の実験の結果によると、物体の運動エネルギー K は、物体の速さを v とし、その物体の質量を m とすると、
である。
運動の方向がどちらであっても、物体が持っているエネルギーは同じである。
運動エネルギーの単位は、ジュール(J)である。
実際に、この量は質量と速度の2乗の積で出来ていることから、この量の単位は
- [kg] [/]
- = [kg ] [m]
- = [N] [m]
となり、確かに仕事の単位(J)と等しいことが分かる。
- 運動エネルギーの式の導出
図のように、質量 m[kg]の物体Aが右向きに進んでいるとしよう。物体Bと衝突してから、物体Aが一定の力 F [N]で物体Bを押しながら、距離 s[m] だけ進んで、静止したとする。
このとき、力が一定なので加速度が一定になり、等加速度直線運動の公式より、
である。
この式を移項して整理すると、
となる。(証明おわり)
速さが2倍になると、運動エネルギーは4倍になる。速さが3倍になると、運動エネルギーは9倍になる。
運動エネルギーと仕事の関係
[編集]質量 m[kg]を持つ物体が、水平方向に速度 v1 [m/s] で運動していた。このときその物体に、ある仕事 W [J]をし、その物体の速度をv2まで引きあげた。
一般に、物体になされた仕事の大きさのぶんだけ、物体のエネルギーが変化する。 この場合、仕事Wと運動エネルギーの関係は
となる。
もし、速度を引き上げるときの力 F が、一定の力だとすると、等加速度直線運動の公式から、さきほどの公式を証明できる。
実際に、等加速度直線運動の公式より、
である。式を移項して整理すれば、
となる。(証明おわり)
力が一定でない場合でも、つまり加速度が一定でない場合でも、微小区間に区切って計算することで、その区間内では加速度が一定と近似できるので、加速度一定の場合と同様の公式が成り立ち、 よって、力が一定でない場合でも、
となる。
位置エネルギー
[編集]位置エネルギー
[編集]高さh[m]に持ち上げた質量m[kg]の物体は、手を離せば、重力によってmg[N]の力を受けながら、地面までの距離hの分だけ落下するので、手を離すと仕事をmgh[J]することになる。 ということは、高さh[m]にある質量m[kg]の物体はエネルギーをmgh[J]ほど持っていることになる。 このような、物体の高さによるエネルギーを位置エネルギー(いちエネルギー、potential energy)という。
位置エネルギーは物体の高さhと物体の質量mと重力加速度gに比例する。位置エネルギーの記号をUで表した場合、位置エネルギーUは
である。
弾性力のする仕事と位置エネルギーの関係
[編集]
ばね に蓄えられるエネルギーも、位置エネルギーと見なしてよい。
例として、図のように、水平に ばね が置いてあるとする。そして、自然長からx[m]伸ばしたとする。このとき、ばね に蓄えられるエネルギー(位置エネルギー)を求めよう。計算の簡単化のため、摩擦は考えないとする。
ばね定数を k[N/m]として、弾性力 F は F=kx [N]とする。
位置エネルギーの場合、仕事 W のぶんだけ、位置エネルギー U が増すのだから、位置エネルギーを求めたいなら、まず仕事 W を求めればよい。
ばねの弾性力 F=kx のする仕事 W を求めるには、横軸に伸びx[m]、縦軸に弾性力F[N]のグラフを求め、そのグラフから図形的に仕事の値を求めればよい。
そのグラフは、右図下のグラフのようになる。 そのグラフから分かるように、 自然長を基準にして、x[m]伸びた場合の弾性力 F=kx のした仕事 W[J] は、
である。
そして、その仕事()と同じ大きさのエネルギーが蓄えられるので、これが、弾性力による位置エネルギーである。 つまり、弾性力による位置エネルギー U[J]は、
である。一般に、弾性力の計算では、この式を公式として扱う。
弾性力による位置エネルギーのことを弾性エネルギー(だんせいエネルギー、elastic energy)ともいう。
さきほどの右図では、伸ばした場合の図だったが、縮めた場合でも、自然長を基準に、同様の公式が成り立つ。
- 例題

自然長から x1[m]伸ばされて静止させていた、水平に置かれた ばね を、さらに伸ばして、自然長から x2 まで伸ばした。
このときの位置エネルギーの差を求めよ。
- 答え
それぞれの位置エネルギーをU2、U1とすれば、
を求めればよい。よって、
- (答え)
である。
※注意. 間違えて、【誤答例→】 【←誤答例】としないように。
保存力
[編集]
重力による位置エネルギーは、重力の仕事についての 仕事の原理 から分かるように、高さによってのみ決まり、その移動途中の経路には寄らない。
重力のほか、ばね の弾性力による、ある時点での弾性エネルギーも、その時点での伸び x[m] によってのみ決まり、その途中の経路には寄らない。
この重力や弾性力のように、途中の経路によらず、その時点での位置のみによって、あるエネルギーが決まる場合、その重力や弾性力などの力を保存力(ほぞんりょく)という。
重力は保存力である。弾性力は保存力である。
※ この単元([[高等学校理科 物理I 運動とエネルギー)ではまだ習わないが、静電気力も保存力である。詳しくは、高等学校理科 物理I 電気などの単元で習う。
いっぽう、動摩擦力は、保存力ではない。
保存力によるエネルギーの値は、始点と終点によってのみ決まる。
力学的エネルギーの保存
[編集]力学的エネルギーの保存
[編集]
図のように、かりに、物体をある高さ h2[m]から高さh1へ落下させたとする。
空気抵抗を無視すれば、重力がした仕事のぶんだけ、運動エネルギーが増加するので、次式(じしき)が成り立つ。
移行して、同じ添字(そえじ)の項をまとめれば、次式が得られる。
となる。
これは、位置エネルギーと運動エネルギーの和が、点Aでも点Bでも同じである。
このことから、位置エネルギーと運動エネルギーの和は一定である法則が得られる。
この法則を 力学的エネルギー保存の法則(law of conservation of energy) という。
なお、運動エネルギーと位置エネルギーをまとめて、力学的エネルギー(りきがくてきエネルギー、mechanical energy)という。
ある物体の全ての力学的エネルギーの和を E[J]とすると、その物体の運動エネルギーを K[J]とし、その物体の位置エネルギーを U[J]としたとき、
である。
滑らかな曲面を滑り落ちる物体の場合
[編集]
図のように、かりに、物体をある高さ h[m]から高さ0へ転がりおろしたとして、高さ0で、その物体の速さ v[m]を測る実験を行なう。計算の簡単化のため、物体の初速度は 0 とする。また、摩擦や空気抵抗は、無視できるとする。
物体が仮に球状の場合、転げ落ちる物体の回転によるエネルギー計算法は、高校レベルを越えて大学レベルの計算になるので、ここでは回転エネルギーを無視できるように、球状ではないと形状とする。
さて、図を見ると分かるように、垂直抗力は運動方向と直角であるので、垂直抗力は仕事をしない。
よって、位置エネルギーの計算では、重力 mg による仕事だけを考えればよい。
なので、重力がした仕事 mgh[J]のぶんだけ、運動エネルギーが増加する。 よって、
となる。
この式を v について解くと、
(計算の簡単化のため、vの符号は正のみとした。)
そして実験結果も、この式 と同じ結果になる。
よって、この場合、式 が物理学的に正しいことになる。(物理学は実験科学であるので、実験的に検証された式は正しい。)
振り子の運動の場合
[編集]
張力は運動方向に垂直なので、仕事をしない。よって、張力による仕事は0であるので、張力によるエネルギー変化は0である。
なので、位置エネルギーと運動エネルギーだけを考えればよい。
したがって、振り子のおもりについても、力学的エネルギー保存の法則が成り立ち、
である。
実際の運動での力学的エネルギー
[編集]実際の運動では、摩擦や空気抵抗などのため、運動している物体は、そのうち静止する。なので、実際の物体では、力学的エネルギーは保存しない。
また、経路によって、物体のエネルギーの大きさが変わってくるので、摩擦力は保存力ではない。
失われたぶんの力学的エネルギー(運動エネルギーと位置エネルギー)は、摩擦のため、熱などになって、周囲に放出される。
なお、摩擦によって放出されるエネルギーのことを摩擦熱(まさつねつ)という。
熱については、くわしくは熱の単元 高等学校理科 物理I/熱 で習う。
- 例題

図のように、傾き θ の荒い面の坂で、位置Aで初速度 V_A[m/s]を与えて、物体を滑らせる場合を考える。その後、物体は、斜面にそってs[m]だけ滑り落ち、物体は位置Bで速度V_B になったとする。
高校物理の、この問題では、動摩擦力の大きさは、一定としてよい。
動摩擦力を f[N] とすると、動摩擦がする仕事 W2[J] は、
である。
いっぽう、重力のする仕事は、
である。
また、図より、
失われたぶんの力学的エネルギーが、摩擦力による仕事と等しいから、次式が成り立つ。
雑題
[編集]- 雑題 1

右図のように、すべり台の上で初速度0で球を転がした場合の運動を考える。 すべり台から飛び出したあとの球は、元の位置までは上がらない。
なぜなら、運動エネルギーがあるからである。






























