中学3年生むけひろがる数学

このページ「中学3年生むけひろがる数学」は、まだ書きかけです。加筆・訂正など、協力いただける皆様の編集を心からお待ちしております。また、ご意見などがありましたら、お気軽にトークページへどうぞ。

不正確な記述が含まれる記事です。詳細はトークページをご覧ください。

中学校数学＞ 中学3年生むけひろがる数学

数学には、中学でならう数学のほかにも、色々な数学があります。

また、次に紹介するもののいくつかは、日本の高校の数学や理科などで、習うものもあります。

ほんの少しだけ見てみましょう。

理科の運動の法則と数学の関係

ボールなどを高いところから落下させるとき、落下した高さを $y$ 〔m〕として、手を話してから経過した時間を $x$ 〔秒〕とすると、およそ $y=5x^{2}$ の関係で落下します。

（※ 正確には約

y={\frac {1}{2}}\times 9.81\times x^{2}

だが（重力加速度の国際標準値は 9.80665 ）、中学生はここまで数値を覚えなくていい。なお、地域によって少々、重力加速度の大きさが違うので（たとえば東京では 9.81 よりも 9.80 のほうが近いと言われる）、高校では重力加速度の数値は

9.8

の2ケタまで覚えればいい。）

中学3年の数学で $y=ax^{2}$ の形の関数を習いましたが、この関数をつかって、高校では、物体の落下などの運動を分析できるようになります。

2次関数 $y=ax^{2}+bx+c$

中学校では $y=ax^{2}$ の形の関数を習いましたが、高校では、さらに $y=ax^{2}+bx+c$ の形の関数を習います。

なお、 $y=ax^{2}+bx+c$ の形の関数のことを 2次関数 といいます。

中学校で「1次関数」というのを習いましたが、「2次関数」とは $y=ax^{2}+bx+c$ の形の関数です。

この2次関数を使うことにより、より一般的な現象が計算できるようになります。

マイナスの数の平方根

2次方程式 $ax^{2}+bx+c=0$ の解の公式で、 $x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}$ というのを、中学校で習っています。

ところで、 $y=x^{2}+2x+5$ をグラフに書くと、この関数はx軸とは交わりません。

$x^{2}+2x+5=0$ について、解の公式に代入しても、

x={\frac {-2\pm {\sqrt {2^{2}-4\cdot 1\cdot 5}}}{2}}={\frac {-2\pm {\sqrt {4-20}}}{2}}={\frac {-2\pm {\sqrt {-16}}}{2}}

のように、 ${\sqrt {-16}}$ のような負の数の平方根が出現してしまいます。

高校で習う数学により、このような数の使い方が分かるようになります。

なお、負の数の平方根のことを「純虚数」（じゅんきょすう）といいます。

${\sqrt {-16}}$ は虚数です。

いっぽう、有理数の集合と無理数の集合をあわせた集合にふくまれる数のことを実数（じっすう）と言います。

虚数は、実数ではないです。

次に言うことは数学的には厳密ではないですが、「実数」とは「数直線上に存在する全ての数」だと思っておけば、中学〜高校レベルでは充分でしょう。

${\sqrt {2}}$ だって、正方形 ABCD の対角線の長さは、辺ABの長さの ${\sqrt {2}}$ 倍ですので（三平方の定理で証明できます）、平方根だって長さとして表わせます。

さて、2つの実数 a,b を用意して、

a+b{\sqrt {-1}}

の形であらわされる数のことを「複素数」（ふくそすう）と言います。

b＝0 とすることで、実数も複素数として扱うことができます。なお（「純虚数」ではなく）「虚数」とは、複素数のうち実数でない複素数のことです（つまり複素数 $a+b{\sqrt {-1}}$ において b≠0 の場合が虚数）。

また、中学の範囲では説明できませんが、複素数をつかうと、a＝0 とすることで（ただし b≠0 ）、 ${\sqrt {-2}}$ や ${\sqrt {-3}}$ などの純虚数もすべて扱えます。

なので、複素数を考えることにより、扱える数の範囲が広がり、二次方程式の解もすべての場合に扱えるようになります。

なお、高校では、さらに ${\sqrt {-1}}$ を文字 $i$ に置き換え、複素数は

a+bi

のような形で表します。（もし ${\sqrt {-1}}$ の形のままで計算すると、計算ミスをしやすいので、文字 $i$ に置き換えて複素数を計算するのが普通である。）

素数ゼミ

（※ 高校数学や高校理科とは、あまり関係の無い話題ですが、いくつかの検定教科書で巻末で紹介している話題なので、ここで一緒に紹介します。）

夏に、ふつうのセミは毎年発生しますが、北アメリカには13年周期で発生する特別なセミと、17年周期で発生する特別なセミがいます。

13と17は素数なので、北アメリカのこのセミは素数ゼミ（そすうゼミ）と言われています。

科学的には仮説ですが、素数ゼミは、天敵の発生の周期となるべくズレた周期で発生したほうが生存しやすいので、進化によって、素数の周期で発生するように進化してきたのだろうと思われています。

たとえば、もし12年周期で発生するセミなら、天敵の発生周期が周期2年や周期3年や周期4年だとすると、天敵に食べられてしまいます。

しかし、13年周期のセミなら、周期2年や3年や4年の天敵とは、あわなくてすみます。

周期1年の天敵にだけが敵なので、だいぶ生存の確率が増えるでしょう。

むかし中学で習ってた内容

中学教育の内容は、定期的に変わるので、むかしは中学で教えてた分野が、いまでは高校で初めて教える分野になっている場合もあります。

次に紹介する「三角形の重心」と「最大公約数と最小公倍数」は、むかしは中学で教えていた時代もありました。

※ 啓林館の教科書で中3の巻末コラムで最大公約数などを紹介しているので、本頁で紹介している。

三角形の重心

ぶあつい画用紙などで作った三角形の模型を、右図のように棒などで支えるとき、どこを支えると、バランスよく、三角形が落ちずに支えられるでしょうか？

じつは、下の図のように、ある頂点から、向かいあう辺の中間点に引いた線分を、比率 2:1 に分割する点で支えると、バランスよく支えられることが分かっています。

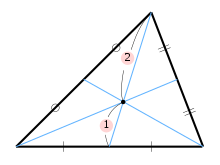
また、このような点のことを三角形の重心（じゅうしん）と言います。

最大公約数と最小公倍数

公約数とは

まず、「約数」（やくすう）という用語があります。

約数とは、ある数を整数（普通は自然数）で割り算したとき、商として現れる数のことです。

たとえば、24の約数は、

24の約数　　1, 2, 3, 4, 6, 8, 12, 24

のようになります。

24÷1＝24 なので、「24」自身も24の約数にふくまれます。

同様に「1」も、24÷24＝1 として整数の割り算の商として表われるので、1も約数にふくまれます。

さて、たとえば 24 と 30 のように2つの数があるとき、

その両方に約数としてふくまれる数があり、これを公約数（こうやくすう）といいます。

24の約数　　1, 2, 3, 4, 6, 8, 12, 24

30の約数　　1, 2, 3, 5, 6, 10, 15, 30

ですので、よって

24と30の公約数は

1, 2, 3, 6

の4個です。

そして最大公約数（さいだいこうやくすう）とは、その名のとおり、公約数のうち、いちばん大きな数のことです。

24と30の最大公約数は 6 です。

なお、2つの数の最大公約数が1の場合、その2つの数を「互いに素」（たがいにそ）と言います。

たとえば、数 8 と数 15 は「互いに素」です。なぜなら、公約数は1しかないからです。

2も3も4も5も6も7も8も、いっさい公約数ではないです。

「2」は8の約数ですが、しかし15の約数ではないです。

「3」は15の約数ですが、しかし8の約数ではないです。

同様に、4から8まで、公約数には、なっていないです。

「7」にいたっては、そもそも、8の約数ではなく、15の約数でもなく、まったく無関係の数になっています。

さて、ある数が「素数」であるかどうかと、「互いに素」とは、別々（べつべつ）の考え方です。混同しないように気をつけましょう。

たとえば、上の8と15の約数の例では、

素数3は15の約数ですが、しかし「互いに素」ではないです。

備考

（※ 範囲外: ）ちなみに、右上の図のように、2つの丸を書いて、その丸の重なった部分に共通部分を書く方法で、なにかを図解したものを「ベン図」といいます。

いまの中学校では、すでに「集合」という考え方を習っています（「自然数の集合」など習っている）。2つの集合の共通部分や、共通でない部分などを図解するさいに、よくベン図が使われます。

「24の約数の集まり」も、ものの集まりなので、数学的には「集合」として扱えます（実際、高校以上の数学では、集合としてあつかう）。

（※ 範囲外: ）自然数の考え方は小学生でも知っているので、よく私立中学の受験問題とかで、こういった公約数などの計算が出題されることがある。なので、「ベン図」や（約数の）「集合」も塾とかで習ったりすることがある。

公倍数とは

2つ以上の倍数に共通する数を 公倍数（こうばいすう）といいます。たとえば 6 と 14 の倍数については、それぞれかき鳴らべると、

6 の倍数　　6, 12, 18, 24, 30, 36, 42, 48, 54…

8 の倍数　　8, 16, 24, 32, 40, 48, 56, …

なので、24 や 48 は、6と8の公倍数です

最小公倍数とは、その名のとおり、公倍数のうち、自然数で最も小さい数です。（負の倍数を考えると、いくらでも小さくできてしまうので、「公倍数」といった場合は自然数だけを考える。）

つまり、24が、6と8の最小公倍数です。

備考

大きな数の最大公約数や最小公倍数を求めるときは、素因数分解をすると、もとめやすい。（くわしくは『高等学校数学A/整数の性質』で習う。私立高校の受験とかで出るかもしれないので、リンクだけ紹介しておく。）

※ 啓林館の中3の検定教科書には、素因数分解をつかった公約数や公倍数の計算なども書いてある。

二進法

むかしは中学で、二進法（にしんほう）などを教えていましたが、2019年の時点では、二進法などは習わなくなっています。現在の日本の教育カリキュラムでは、二進法の単元は、高校の『数学1A』に移動しています。

※ 2019年、学校図書の巻末コラムで二進法の話題があり、 2038年問題を紹介している。

小学校でならう、1 → 2 → 3 → …… → 7 → 8 → 9 → 10 のような数え方は十進数（じっしんすう）といいます。

二進法とは、 1 → 10 → 11 → 100 → 101 →・・・のように、0と1だけで整数を表す数え方です。

むかし、中学の数学教育では「二進法がコンピュータに使われてる」などと教えていました。現在のコンピュータでも、コンピュータ内部の計算で二進法が使われている事じたいは、同じままです。

さて、現代のパソコン利用者とって身近なところでは、

お絵描き系のソフトとかで色を調整するとき、よく

「赤:255　緑:30　青:100」

みたいに、ある色の、色のつよさを0から最大で255まで、色を強くできます。

この「255」の数字の由来は、

十進数の式

2×2×2×2 × 2×2×2×2 − 1 ＝ 256 − 1

が由来です。（かけ算で 2 が 8個）

この255（十進数）は、2進数で表すと

1111 1111 （2進数）です。

です。（ケタ数が多いので、4つずつで区切るのが普通。）

「256」でなく「255」なのは、コンピュータ内部ではゼロから数字を数えているため、0から255までの数字の数が256個だからです。

つまり、

「赤:255　緑:30　青:100」

のような色のデータの形式では、色の三原色あたり、2進数で8ケタずつのデータを確保している事になります。

そして、三原色というように、3つの原色のつよさの比で色を表しているので、合計で 3×8 ＝ 24 で、24ケタの2進数で色を表すことになります。

「24ビットカラー」というのは、このようなデータ形式で色を管理しているという意味です。

暗号と素因数分解

※ 高校の『情報』教科で習うでしょう。

現在のインターネットなどコンピュータ環境でよく利用されている暗号として、RSA暗号（アールエスエーあんごう）というのがありますが、この暗号は原理として素因数分解を利用しています。

たとえば、37 × 71 ＝ 2627 というのは筆算をすればいいだけなので簡単ですが、

しかし、いきなり「2627」という数字を、もし貴方が見せられて、それを「素数か、素数でないかを判定してください。もし素数でないなら、素因数分解してみなさい」といわれても、むずかしいでしょう。

じっさいに、たとえば「5371」という数字をいきなり出されて、これが「素数であるかどうかを判定して」と言われても、コンピュータも何も持ってない人には、むずかしいでしょう。（ちなみに 5371 は素数ではなく、41×131＝5371 です。）

2つの大きな素数のかけ算を素因数分解するのは、一般に難しいという性質を、RSA暗号は利用しています。

統計のばらつき

たとえば、少人数学級の中学校があり、1クラスの生徒数が9人で、1つの学年に学級が2クラスあるとしましょう。ある科目のクラス平均点は、

3年A組の平均点は 50点で、

3年B組の平均点も 50点

だったとしましょう。

そして、補習はテストで30点以下だった生徒に対して行われる学校だとしましょう。

しかし、A組のほうは補習をうけさせられる30点以下の成績をとっている生徒が1人ですが、B組のほうは補習をうけさせられる30点以下の生徒が4人もいたとして、

実際のそれぞれの生徒の得点の分布が

A組の生徒3人の得点は、それぞれ、1人目が10点、 2人目が50点、 3人目が50点、 4人目が50点、 5人目が50点、 6人目が50点、 7人目が50点、 8人目が50点、 9人目が90点、

B組の生徒3人の得点は、ぞれぞれ、1人目が10点、 2人目が10点、 3人目が10点、 4人目が10点、 5人目が50点、 6人目が90点、 7人目が90点、 8人目が90点、 9人目が90点、

だったとしましょう。

A組とB組は、平均点（50点）だけで見ると同じですし、範囲（10〜90の範囲である）も同じですが、しかし、クラス内の得点の事情が、かなり違っています。

A組とB組は、平均も範囲も同じなのに、なのにA組のほうは、補習をうける生徒は,10点をとっている1人目の生徒1人だけなのに、いっぽうB組のほうは、クラス9人中の半数ちかい4人の生徒が10点ですので、B組では補習をクラスの半分ちかくが受けます。

なのに、「平均」と「範囲」いう考え方だけでは、このような散らばりの程度を表現できないので、新しい考え方が必要です。

そこで、高校で習う「分散」（ぶんさん）や「標準偏差」（ひょうじゅんへんさ）という概念を使うと、このような　ばらつき　の程度を、数値的に表せるようになります。

なお、「分散」は

（（資料の個々の値） − （平均値））² の合計を資料の個数で割った値

で定義されます。

（※ 教育出版の検定教科書では、分散の定義まで、教える）

標準偏差は分散の平方根です。例では、数えやすいように、たったの9人のクラスにしましたが、実際の社会では、もっと多くのものの統計を数えるわけです。

たとえば、もし9人の受けたテストでなくて、900人の受けたテストだったら…という場合もあるわけです。

備考　「偏差値」とは

よく受験産業でいう「偏差値」（へんさち）を求める計算には、この「分散」や「標準偏差」が利用されています。

背理法

中学では ${\sqrt {2}}$ が、けっして ${\frac {2}{5}}$ や ${\frac {13}{7}}$ のような整数だけを分子と分母にもつ分数では表せないこと（つまり無理数であるという事）を習っていますが、しかし、その証明は習っていません。

高校の数学で、その証明を習います。

証明の方法は、おおまかに言うと、

いったん、

{\sqrt {2}}

が整数だけを分子と分母にもつ分数で表せると仮定して、　　　（1）

すると、矛盾が起きることを証明し、

矛盾が起きないようにするためには、　（1）の仮定が間違っていなければならない、として　（1）の反対の内容を証明する方法です。

上述のような、証明したい内容と反対のことを仮定して矛盾をみちびくことにより、証明したい内容を証明する論法のことを 背理法（はいりほう）といいます。

${\sqrt {2}}$ だけでなく ${\sqrt {3}}$ や ${\sqrt {5}}$ も同様にして、無理数であることを証明できます。

また、素数がかぎりなく存在することも背理法で証明できます。

三角関数

中学校では、右の図のように、60°などといった角度が特別な角度の直角三角形について、3辺の長さの比が決まっている事を習った。

しかし、直角三角形の相似の条件を考えれば、角度が50°や75°などの角度であっても、3辺の比率は決まるはずである。

そこで高校では、もはや 60°や45°などの特別な角度でなくても、3辺の長さの比が決まることを利用して、斜辺の基準にして比率を求める。

直角三角形の斜辺と高さの比率を

（直角三角形の高さ）/（斜辺の長さ）

で表したものを「正弦」（せいげん）といい、記号では「 sin 」（サイン）という記号を使って

sin （角度）

のような記法で表す。

具体例をあげると

\sin 60^{\circ }={\frac {\sqrt {3}}{2}}

である。

角度が50°の直角三角形については、分度器（ぶんどき）や定規（じょうぎ）などを使って実際に書いてみれば、 3辺の長さの比を測定することができる。

なので、sin 50° の近似値を求めることもできる。

実際に求めてみると、

\sin 50^{\circ }\fallingdotseq 0.7660

である。

\fallingdotseq

は「この記号の左右の式は、ほぼ近い値」という意味。

おまけ

なお、「コサイン」とか「タンジェント」という言葉も、三角関数の一種です。

コサインは

（コサイン）＝（直角三角形の底辺の長さ）/（斜辺の長さ）

（タンジェント）＝（直角三角形の高さ）/（直角三角形の底辺の長さ）

です。

コサインは記号で cos と表します。

タンジェントは記号で tan と表します。

そして、「sin （角度）」の記法と同様に、cos や tan の後ろに角度を書きます。

\cos 60^{\circ }={\frac {\sqrt {1}}{2}}

　,　　

\tan 60^{\circ }={\frac {\sqrt {3}}{1}}={\sqrt {3}}

です。

詳しくは高校で習うので、ここでは、これより深くは解説しないでおきます。

放射性年代測定と指数

中学で 3²＝9 のように「指数」（しすう）という考えかたを習いました。

ところで、歴史の研究の分野で使う放射性年代測定（ほうしゃせいねんだいそくてい）では、

放射性物質の強さが一定の年月が経つと半分ずつになっていく事を、年代測定に利用しています。

放射性炭素が半分になるのは､約 5730年の時間が掛かります。ここでいう「炭素」とは、理科で習う元素記号 C の炭素のことです。通常の炭素とは別に、放射性炭素がわずかながら空気中に存在しています。

くわしい原理の理解には、高校で習う理科の化学（かがく）などの知識も必要なので、中学では解説しきれないのですが、

放射性年代測定には、指数の計算も必要になります。

たとえば、放射能のつよさが半分になる一定の年月が $x$ 回だけ経過したとすると、その放射能の強さは、もとの放射能の強さを a とすると

a\cdot ({\frac {1}{2}})^{x}

のように、指数をつかった数式で表すこともできます。

たとえば放射性炭素の場合、

5730 年 × 3 ＝ 17190 年

なので、

17190年後の放射能の強さは、もとの放射能の強さの $({\frac {1}{2}})^{3}$ 倍、つまり、もとの強さの8分の1になっているわけです。

「未解決問題」とは

数学の世界には、まだ、人類のだれにも答えが知られてない難問もあります。そのような、まだ誰にも解かれてない数学の問題のことを「未解決問題」（みかいけつもんだい）といいます。

中学でも、問題の意味が理解できるような未解決問題もあります。

たとえば、ゴールドバッハ予想という未解決問題の内容は、

「4以上のすべての偶数は、2つの素数の和であらわすことができる」

というものです。

たとえば、

4＝2＋2

6＝3＋3

8＝5＋3

10＝3＋7

などです。

まだ誰にも、この予想は証明されていないのです。

※ 学校図書の検定教科書がゴールドバッハ予想を紹介している。

理科の運動の法則 と 数学の関係

2次関数 y = a x 2 + b x + c {\displaystyle y=ax^{2}+bx+c}