初等数学公式集/初等幾何/体積

このページでは体積の公式の解説をします。

直方体の体積

V = abh

立方体の体積

V = a³

柱体の体積

V = Sh

錐体の体積

$V={\frac {1}{3}}Sh$

錐体

錐体の頂点から底面$S$（右図では$A_{b}$）に垂線を下して、頂点から$x(0\leq x\leq h)$の距離で底面と平行に錐体を切り取ったことで得られる図形を$A_{x}$とする。

この時、錐体の定義から、$S$と$A_{x}$は相似である。

相似な図形の面積比は、相似比の２乗に等しいことから、

$S:A_{x}=h^{2}:x^{2}$

従って、

$A_{x}={\frac {x^{2}S}{h^{2}}}$

錐体の体積は、平面図形$A_{x}$に関して、$0\leq x\leq h$の区間で変化させ累積したものであるから、$A_{x}$を区間$[0,h]$で積分することにより得られる。

$V=\int _{0}^{h}A_{x}\,dx$ $=\int _{0}^{h}{\frac {x^{2}S}{h^{2}}}\,dx$ $={\frac {S}{h^{2}}}\int _{0}^{h}x^{2}\,dx$ $={\frac {S}{h^{2}}}\left[{\frac {x^{3}}{3}}\right]_{0}^{h}$ $={\frac {S}{h^{2}}}\left({\frac {h^{3}}{3}}\right)$$={\frac {1}{3}}Sh$

錐台の体積

錐台

上底の面積 $s$（右図では$A_{2}$）、下底の面積 $S$（右図では$A_{1}$）、高さ $h$ の錐台の体積 $V$

錐台は、別名「切頭錐体」のとおり、$S$を底とする錐体:$P_{1}$から、$s$を底とする相似な錐体:$P_{2}$を除いたものとされる。

錐体:$P_{1}$の高さを $H$とすると、錐体:$P_{2}$の高さは $H-h$となり、各々の体積は、

$V_{1}={\frac {1}{3}}SH$, $V_{2}={\frac {1}{3}}s(H-h)$ となるので、求める体積$V={\frac {1}{3}}(SH-s(H-h))={\frac {1}{3}}(H(S-s)+hs))$(※)となる。

相似比と面積比の関係から、

$S:s=H^{2}:(H-h)^{2}$

従って、

${\sqrt {S}}:{\sqrt {s}}=H:(H-h)$

$H{\sqrt {s}}=(H-h){\sqrt {S}}$

$H({\sqrt {S}}-{\sqrt {s}})=h{\sqrt {S}}$

$H={\frac {h{\sqrt {S}}}{{\sqrt {S}}-{\sqrt {s}}}}$$={\frac {h{\sqrt {S}}({\sqrt {S}}+{\sqrt {s}})}{S-s}}$$={\frac {h(S+{\sqrt {sS}})}{S-s}}$

これを、※に代入すると、以下の式を得る。

$V={\frac {h}{3}}(s+{\sqrt {sS}}+S)$

くさび形の体積

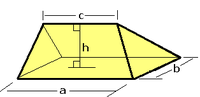くさび形

• 下底が 縦のながさ a、横のながさ bの長方形、縦と平行である上辺のながさ c、高さ h のくさび形の体積 V：

  $V=bh\left({\frac {a}{3}}+{\frac {c}{6}}\right)$

くさび形の上辺から底面に垂線を下して、頂点から$x(0\leq x\leq h)$の距離で底面と平行にくさび形を切り取ったことで得られる図形（長方形）を$S_{x}$とする。

この長方形の縦横は比例の関係から以下のとおりとなる。

• 縦:${\frac {(a-c)x}{h}}+c$, 横:${\frac {bx}{h}}$
• $S_{x}=\left({\frac {(a-c)x}{h}}+c\right)\left({\frac {bx}{h}}\right)$$={\frac {(a-c)bx^{2}}{h^{2}}}+{\frac {bcx}{h}}$

くさび形の体積は、平面図形$S_{x}$に関して、$0\leq x\leq h$の区間で変化させ累積したものであるから、$S_{x}$を区間$[0,h]$で積分することにより得られる。

$V=\int _{0}^{h}S_{x}\,dx$ $=\int _{0}^{h}\left({\frac {(a-c)bx^{2}}{h^{2}}}+{\frac {bcx}{h}}\right)dx$ $={\frac {b}{h^{2}}}\int _{0}^{h}((a-c)x^{2}+chx)dx$ $={\frac {b}{h^{2}}}\left[{\frac {(a-c)x^{3}}{3}}+{\frac {chx^{2}}{2}}\right]_{0}^{h}$ $={\frac {b}{h^{2}}}\left({\frac {(a-c)h^{3}}{3}}+{\frac {ch^{3}}{2}}\right)$$=bh\left({\frac {a}{3}}+{\frac {c}{6}}\right)$

正多面体の体積

正四面体の体積

$V={\frac {\sqrt {2}}{12}}a^{3}$

まず底面から計算します。

正四面体の頂上の頂点は、底面を形成する3点から等しい位置にあるので、

そこから真下へ線を伸ばしたとき、その線と底面との交点は、3点から等しい位置、即ち中心(外心、内心、重心、垂心)に位置することになります。

さらに底面の図形は正三角形なので、それぞれの点から中心をとおり、対辺に繋がる線分を引くと、3線全てが、対辺を垂直に2等分します。

このとき、この線分の長さ(右図上の赤線の長さ)は、三平方の定理によって、

${\begin{matrix}{\sqrt {{\color {Green}a}^{2}-\left({1 \over 2}a\right)^{2}}}&=&{\sqrt {{\color {Green}a}^{2}-{1 \over 4}a^{2}}}\\\\&=&{\sqrt {{3 \over 4}a^{2}}}\\\\&=&{\color {Red}{{\sqrt {3}} \over 2}a}\end{matrix}}$

次に青線2本と緑線1本で形成される二等辺三角形に、緑線を対象の軸とした線対称な二等辺三角形を作図します。

この二等辺三角形は、底角が30ﾟ(正三角形の角の2等分線であるため)なので、2つ繋げると60ﾟになります。

2辺が等しく、その間の角が60ﾟである二等辺三角形は正三角形なので、

右図上の黒線全体の長さは、青線の長さに等しく、二等辺三角形の頂角の二等分線は、底辺を垂直に2等分するため、

この黒線のうち正三角形の内側に入る黒線の長さは、青線の長さの半分、つまり、赤線の長さの${1 \over 3}$となります。

逆に青線の長さは赤線の長さの${2 \over 3}$なので、

${\begin{matrix}{\color {Red}{{\sqrt {3}} \over 2}a}\times {2 \over 3}&=&{{\sqrt {3}}\times 2\!\!\!/ \over 2\!\!\!/\times 3}a\\\\&=&{\color {Blue}{{\sqrt {3}} \over 3}a}\end{matrix}}$

続いて高さ。高さはこれまでに調べた長さと三平方の定理を利用すれば、

${\begin{matrix}{\sqrt {{\color {Green}a}^{2}-\left({\color {Blue}{{\sqrt {3}} \over 3}a}\right)^{2}}}&=&{\sqrt {{\color {Green}a}^{2}-{1 \over 3}a^{2}}}\\\\&=&{\sqrt {{2 \over 3}a^{2}}}\\\\&=&{\color {Brown}a{\sqrt {2 \over 3}}}\end{matrix}}$

底面積、高さが出たので、

${\begin{matrix}V&=&{\color {Green}a}\times {\color {Red}{{\sqrt {3}} \over 2}a}\times {1 \over 2}\times {\color {Brown}a{\sqrt {2 \over 3}}}\times {1 \over 3}\\\\&=&{{\color {Green}a}\times {\color {Red}a{\sqrt {3}}\!\!\!/}\times {\color {Brown}a{\sqrt {2}}} \over 2\times {\color {Red}2}\times 3\times {\color {Brown}{\sqrt {3}}\!\!\!/}}\\\\&=&{{\sqrt {2}} \over 12}a^{3}\end{matrix}}$

立方体から考える

正四面体の体積は、立方体との関係からも導出することができます。
立方体と頂点を共有した正四面体は、全ての辺が立方体の面の対角線になっています。
よって、立方体から余った体積を引けば、正四面体の体積を導き出すことができます。

正四面体の1辺の長さをaとします。
余った部分は全部で4つありますが、辺の長さは全てそれぞれ等しいので、これらは合同になります。

立方体の1辺の長さは、正方形の辺と対角線の長さの比「$1:{\sqrt {2}}$」から、

$a\times {\frac {1}{\sqrt {2}}}={\frac {\sqrt {2}}{2}}a$

余った部分は三角錐とみなすことができるので、角錐の体積から、

${\frac {1}{3}}\times {\frac {1}{2}}\times {\frac {\sqrt {2}}{2}}a\times {\frac {\sqrt {2}}{2}}a\times {\frac {\sqrt {2}}{2}}a$

$={\frac {1}{6}}\times \left({\frac {\sqrt {2}}{2}}a\right)^{3}$

$={\frac {1}{6}}\times {\frac {\sqrt {2}}{4}}a^{3}$

$={\frac {\sqrt {2}}{24}}a^{3}$

最後に立方体から角錐4つを引きます。

$\left({\frac {\sqrt {2}}{2}}a\right)^{3}-4\left({\frac {\sqrt {2}}{24}}a^{3}\right)$

$={\frac {\sqrt {2}}{4}}a^{3}-{\frac {\sqrt {2}}{6}}a^{3}$

$={\frac {3{\sqrt {2}}}{12}}a^{3}-{\frac {2{\sqrt {2}}}{12}}a^{3}$

$={\frac {\sqrt {2}}{12}}a^{3}$

正八面体の体積

$V={\frac {\sqrt {2}}{3}}a^{3}$

高さは底面の対角線の交点から求めることができます。

正八面体は、体積の等しい正四角錐が2つあると見ることができます。
それらの角錐の高さは、角錐の底面の対角線の交点から求めることができます。
底面に対し、頂上の頂点と底面の対角線の交点を結ぶ直線は垂直になるので、
高さは、角錐の母線と対角線から、三平方の定理で導出できます。

対角線の長さは、

${\sqrt {a^{2}+a^{2}}}=a{\sqrt {2}}$

対角線は互いの中点で交わるので、

${\frac {a{\sqrt {2}}}{2}}$

高さは、母線と対角線の半分から、

${\sqrt {a^{2}-\left({\frac {a{\sqrt {2}}}{2}}\right)^{2}}}$

$={\sqrt {a^{2}-{\frac {a^{2}}{2}}}}$

$={\sqrt {\frac {a^{2}}{2}}}$

$={\color {red}{\frac {a{\sqrt {2}}}{2}}}$

実は、正八面体はどこで正四角錐2つに分離しても、高さは同一であるため、対角線の半分が既に高さになっています。
最後に、錐体の体積の公式から、

$V=2\times {\frac {1}{3}}\times a^{2}\times {\color {red}{\frac {a{\sqrt {2}}}{2}}}$

$={\frac {1}{3}}\times {\sqrt {2}}a^{3}$

$={\frac {\sqrt {2}}{3}}a^{3}$

正十二面体の体積

$V={\frac {15+7{\sqrt {5}}}{4}}a^{3}$

正二十面体の体積

$V={\frac {5(3+{\sqrt {5}})}{12}}a^{3}$

球の体積

$V={\frac {4}{3}}\pi r^{3}$

$x^{2}+y^{2}+z^{2}=r^{2}$である球を考える。

$x=t$でこの球を切断すると、半径${\sqrt {r^{2}-t^{2}}}$である円;$C$を得るが、この円;$C$の面積は$\pi (r^{2}-t^{2})$である。

球の体積は、この円;$C$に関して、$-r\leq t\leq r$の区間で変化させ累積したものであるから、$\pi (r^{2}-t^{2})$を区間$[-r,r]$で積分することにより得られる。

$V=\int _{-r}^{r}\pi (r^{2}-t^{2})\,dt$ = $\pi \int _{-r}^{r}(r^{2}-t^{2})\,dt$ = $\pi \int _{-r}^{r}(r^{2}-t^{2})\,dt$ = $\pi \left[tr^{2}-{\frac {t^{3}}{3}}\right]_{-r}^{r}$ = $\pi \left\{\left(r^{3}-{\frac {r^{3}}{3}}\right)-\left(-r^{3}+{\frac {r^{3}}{3}}\right)\right\}$ = ${\frac {4}{3}}\pi r^{3}$

円環体（トーラス）の体積

円環体・トーラス

半径$r$の円;$C$を、円の中心からの距離$R$（但し、$r$　≦　$R$とする）の直線を軸として回転させた円環体（トーラス、ドーナツ型）

（参考）

• この時、 半径$r$を「小半径」、半径$R$を「大半径」と呼ぶこともある。
• 円環体の内縁部の円の半径$a$と外縁部の円の半径$b$が与えられることもある。この時は、以下の関係を利用し考察。

  $r={\frac {-a+b}{2}}$, $R={\frac {a+b}{2}}$

円環体の切断図形

(解法)

円;$C$の中心から距離$t$（0≦$t$≦$r$）の位置で、円環体の回転軸に垂直に切り取ると、半径;$R-{\sqrt {r^{2}-t^{2}}}$の円を内側の円;$C_{1}$とし、半径;$R+{\sqrt {r^{2}-t^{2}}}$の円;$C_{2}$を外側の円とする図形が得られる。

この図形の面積を$S$とすると、

$S=\pi \left(R+{\sqrt {r^{2}-t^{2}}}\right)^{2}-\pi \left(R-{\sqrt {r^{2}-t^{2}}}\right)^{2}=4\pi R{\sqrt {r^{2}-t^{2}}}$

これを、$0\leq t\leq r$の区間で変化させ累積すると、円環体の1/2の体積;$V_{h}$が得られる。

$V_{h}=\int _{0}^{r}4\pi R{\sqrt {r^{2}-t^{2}}}dt=4\pi R\int _{0}^{r}{\sqrt {r^{2}-t^{2}}}dt$

$\int _{0}^{r}{\sqrt {r^{2}-t^{2}}}dt$ を解く。（置換積分法を利用）

• $t=r\sin {\theta }$と置く。

$t$を$\theta$で微分すると、${\frac {dt}{d\theta }}=r\cos {\theta }$、$\therefore$　$dt=r\cos {\theta }d\theta$

• $t=0$の時、$\theta =0$
• $t=r$の時、$\theta ={\frac {\pi }{2}}$

$\int _{0}^{r}{\sqrt {r^{2}-t^{2}}}dt=\int _{0}^{\frac {\pi }{2}}{\sqrt {r^{2}-r^{2}\sin ^{2}\theta }}\cdot (r\cos {\theta })d\theta =r^{2}\int _{0}^{\frac {\pi }{2}}{\sqrt {1-\sin ^{2}\theta }}\cdot (\cos {\theta })d\theta$

$=r^{2}\int _{0}^{\frac {\pi }{2}}\cos ^{2}\theta d\theta$ ($\because$ ${\sqrt {1-\sin ^{2}\theta }}={\sqrt {\cos ^{2}\theta }}=|cos\theta |$、$0\leq \theta \leq {\frac {\pi }{2}}$であるので、$=cos\theta$)

$=r^{2}\int _{0}^{\frac {\pi }{2}}{\frac {1+\cos 2\theta }{2}}d\theta$ ($\because$ $\cos ^{2}\theta ={\frac {1+\cos 2\theta }{2}}$)

$=r^{2}\left[{\frac {\theta }{2}}+{\frac {\sin 2\theta }{4}}\right]_{0}^{\frac {\pi }{2}}={\frac {r^{2}\pi }{4}}$

$V_{h}=4\pi R\cdot {\frac {r^{2}\pi }{4}}=\pi ^{2}r^{2}R$

$\therefore$　 $V=2\pi ^{2}r^{2}R=(\pi r^{2})(2\pi R)$

後式は、「平面上にある図形$F$の面積を$S$とし、$F$と同じ平面上にあり$F$を通らない軸$l$の周りで$F$を一回転させた回転体の体積を$V$とする。回転させる図形$F$の重心$G$から回転軸$l$までの距離を$R$としたとき、

$V=2\pi RS$

が成り立つ」というパップス＝ギュルダンの定理第二定理と一致している。