出典: フリー教科書『ウィキブックス(Wikibooks)』
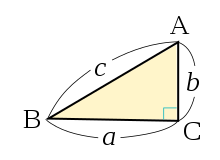
- 直角三角形の直角をはさむ2辺の長さをa、b、斜辺の長さをcとすると、以下の関係が成り立つ。:

- 三角形の三辺の長さa,b,cが
 を満たすとき、この三角形は長さcの辺を斜辺とする直角三角形となる。
を満たすとき、この三角形は長さcの辺を斜辺とする直角三角形となる。
(参考) 三平方の定理
 において、
において、 , 外接円の半径を
, 外接円の半径を  とすると、
とすると、

(参考)正弦定理

一辺とその両端の角の大きさがわかっている時の、他の辺及び当該三角形の既知の辺に対する高さ(三角測量の原理)。
- 右の図において辺
 が既知である時、
が既知である時、



-
 ,
, 
 において、
において、 とすると
とすると






(参考)余弦定理
 中線定理
中線定理
- 中線定理
- 三角形の辺
 の長さを
の長さを  とする。辺
とする。辺  上の中点
上の中点  を取り、
を取り、 を
を  とすると、以下の式が成り立つ。
とすると、以下の式が成り立つ。

- 別形:
 (なお、
(なお、 )
)
-
- (証明)
 として、第2余弦定理より、
として、第2余弦定理より、
 、従って、
、従って、 - ①
- ①
- 同様に、
 、従って、
、従って、 - ②
- ②
- ①、②から、

-

-

 スチュワートの定理
スチュワートの定理
- スチュワートの定理
- 三角形の辺
 の長さを
の長さを  とする。辺
とする。辺  上に点
上に点  を取り、
を取り、 を
を  とする。
とする。 の長さを
の長さを  とすると、以下の式が成り立つ。
とすると、以下の式が成り立つ。

 が辺の中点(
が辺の中点( )のとき、この式は中線定理の式に一致する。
)のとき、この式は中線定理の式に一致する。
 において、
において、 とすると
とすると

 メネラウスの定理。A→F→B→D→C→E→Aの順で循環する。
メネラウスの定理。A→F→B→D→C→E→Aの順で循環する。
- メネラウスの定理
- 任意の直線
 と
と において、直線
において、直線 と
と の交点をそれぞれ
の交点をそれぞれ とする。この時、次の等式が成立する。
とする。この時、次の等式が成立する。

- チェバの定理
 において、任意の点
において、任意の点 をとり、直線
をとり、直線 と
と 、
、 と
と 、
、 と
と の交点をそれぞれ
の交点をそれぞれ とする。この時、次の等式が成立する。なお、点
とする。この時、次の等式が成立する。なお、点 は、三角形の内部にあっても外部にあってもよい。
は、三角形の内部にあっても外部にあってもよい。

 チェバの定理。点Oが三角形の内部にある場合 チェバの定理。点Oが三角形の内部にある場合
|
 チェバの定理。点Oが三角形の外部にある場合 チェバの定理。点Oが三角形の外部にある場合
|
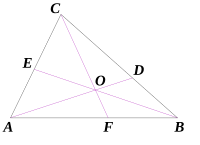
- 三角形の頂点から相対する辺の中点に対して下ろした線分のことを中線という。各々の頂点から下ろした線分は一点で交わり、その点を重心(通常、
 で表記される)という。
で表記される)という。
- 重心は中線を角側から見て、2:1 に内分する。
- (参照:ベクトルによる表記)
 三角形の重心 三角形の重心
|
- 三角形の3つの辺の垂直二等分線は1点で交わり、その点を外心(通常、
 で表記される)という。
で表記される)という。
- 外心は、三角形の外接円の中心である。= 外心から各角との距離は等しい。
- (参照:ベクトルによる表記)
 各辺の垂直二等分線と外心 各辺の垂直二等分線と外心
|
 外心と外接円 外心と外接円
|
- 三角形の3角のそれぞれに対して角の二等分線を取ったとき、それぞれの直線は1点で交わり、その点を内心(通常、
 で表記される)という。
で表記される)という。
- 内心は、三角形の内接円の中心である。= 内心から各辺との距離は等しい。= 内心から内接円と辺の接点とを結ぶ線分は内接円の半径であり、辺に対して垂直。
- (参照:ベクトルによる表記)
 各角の二等分線と内心 各角の二等分線と内心
|
 内心と内接円 内心と内接円
|
- 三角形の各頂点から対辺またはその延長に降ろした垂線は、1点で交わり、その点を垂心(通常、
 で表記される)という。
で表記される)という。
- (参照:ベクトルによる表記)
 三角形の垂心 三角形の垂心
|
- 三角形の2つの外角のそれぞれの二等分線と、残りの1つの内角の二等分線とは、一点で交わり、その点を傍心という。
- 傍心は各々の頂点に対する辺の反対側に存在するため、3個存在する。
- 傍心から、それに相対する辺までの距離を半径とする円は、相対する辺以外の各辺を延長した直線と接し、この円を傍接円という(下図参照)。
- (参照:ベクトルによる表記)
 三角形の傍心のひとつ 三角形の傍心のひとつ
|
 オイラー線
オイラー線
- オイラー線
- 三角形の外心・重心・垂心は同一の直線上にある。この直線をオイラー線という。
- 右図において、
- 青の線の交点が垂心

- 橙色の線の交点が重心

- 緑の線の交点が外心

- であって、
 は一直線上(赤線)にある。
は一直線上(赤線)にある。
 垂心の性質
垂心の性質
- 垂心の性質
 に関して、
に関して、 と辺
と辺 に対して反対側に、四角形
に対して反対側に、四角形 が平行四辺形となるような点
が平行四辺形となるような点 をとる。同様に
をとる。同様に に対する点
に対する点 、
、 に対する点
に対する点 をとり、
をとり、 の各辺が中線となる
の各辺が中線となる (
( と相似比1:2の三角形)を得た時、
と相似比1:2の三角形)を得た時、 の垂心
の垂心 は、
は、 の外心となる。
の外心となる。
 三角形の内接円と傍接円
三角形の内接円と傍接円
- 三角形の内接円と傍接円
- 傍心は三角形の二等分線上にあるので、三角形の相対する角と内心の同一直線上にある。
- 三角形の内心は、3つの傍心で作る三角形の垂心に一致する。
 角形の内角の和:
角形の内角の和:

 角形の対角線の本数:
角形の対角線の本数:

- 半径
 の円の円周
の円の円周 :
:

- 半径
 、中心角
、中心角 (度)の扇形の弧の長さ
(度)の扇形の弧の長さ :
:

- 半径
 の円の中心点
の円の中心点 と弦
と弦 との距離を
との距離を としたときの弦
としたときの弦 の長さ:
の長さ:

 中心角と円周角
中心角と円周角
- 円周上の点
 の各々から円の中心点
の各々から円の中心点 に線分を引いた時、
に線分を引いた時、 を中心角という。
を中心角という。
- 円周上の点
 の各々から、円周上の点
の各々から、円周上の点 に線分を引いた時、
に線分を引いた時、 を円周角という。
を円周角という。
- 円周角の定理
- 円周上にとる点の位置に関わりなく、円周角の大きさ
 は対応する円弧※を含む扇形の中心角の大きさ
は対応する円弧※を含む扇形の中心角の大きさ のみに依存し、以下のように表わされる。
のみに依存し、以下のように表わされる。
- ※:対応する円弧:
 ならば、円周上の点
ならば、円周上の点 は、線分
は、線分 から見て中心と同じ側にあり、
から見て中心と同じ側にあり、 ならば、逆側にある。
ならば、逆側にある。

- 右図において、
- 円周角
 と
と は等しい。この時の中心角の大きさを
は等しい。この時の中心角の大きさを とすると、
とすると、 。
。
- 円周角
 と
と は等しい。この時の中心角の大きさを
は等しい。この時の中心角の大きさを とすると、
とすると、 。
。
- したがって、円に内接する四角形の相対する角の和は、
 (=180°)となる。
(=180°)となる。
- タレスの定理
- 円周上の点
 を結ぶ線分
を結ぶ線分 が円の中心
が円の中心 をとおる時(すなわち、線分
をとおる時(すなわち、線分 が直径である時)、点
が直径である時)、点 と円周上の点
と円周上の点 との間になす角
との間になす角 は直角である。
は直角である。
- 逆である「点
 と円周上の点
と円周上の点 との間になす角
との間になす角 が直角であるならば、線分
が直角であるならば、線分 は円の中心
は円の中心 をとおる」もまた真である。
をとおる」もまた真である。
 接線と弦の作る角
接線と弦の作る角
- 接線と弦の作る角
- 三角形のある一点において外接円の接線を引いた時、接線と弦の作る角(右図において角
 )は、三角形の弦に対する角(右図において角
)は、三角形の弦に対する角(右図において角 )に等しい。
)に等しい。
 角
角 をなす弦の
をなす弦の ではない点を
ではない点を 、角
、角 のある点を
のある点を とする。
とする。
 は、
は、 を円周角とする中心角なので、
を円周角とする中心角なので、
 は、
は、 である二等辺三角形。したがって、
である二等辺三角形。したがって、

 において、
において、 と接線は直角をなしているから、接線と弦の作る角
と接線は直角をなしているから、接線と弦の作る角
- 点Pを通る2本の直線が円とそれぞれ2点
 と2点
と2点 で交わっているとき(図1、図2):
で交わっているとき(図1、図2):

- 円外の点
 を通る2本の直線の一方が点
を通る2本の直線の一方が点 で円に接し、他方が2点
で円に接し、他方が2点 で交わっているとき(図3):
で交わっているとき(図3):

 方べきの定理・図1 方べきの定理・図1
|
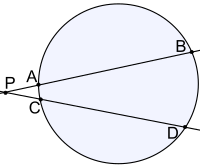 方べきの定理・図2 方べきの定理・図2
|
 方べきの定理・図3 方べきの定理・図3
|
(参考) 方べきの定理
- 縦の長さa、横の長さb、高さh の直方体の対角線 l:

- 底面の半径をr、母線の長さ lの円錐の高さ h:

- 凸面体の頂点の数をv、辺の数をe、面の数をfとすると以下の関係が成り立つ(オイラーの多面体定理):

解説はこちらのページをご覧ください
- 三角形
- 底辺のながさ
 、高さ
、高さ  の三角形の面積
の三角形の面積  :
:

- 二辺のながさが
 ,
,  でその間の角が θ である三角形の面積
でその間の角が θ である三角形の面積  :
:

- ある辺のながさが
 でその両端の角が θ, δ である三角形の面積
でその両端の角が θ, δ である三角形の面積  :
:

- ※上記「正弦定理の応用」で、底辺と両端の角から高さが求められることを利用。
- 三辺のながさが
 ,
,  ,
,  で内接する円の半径が
で内接する円の半径が  である三角形の面積
である三角形の面積  :
:

- [三辺のながさが
 ,
,  ,
,  である三角形の面積
である三角形の面積  :(ヘロンの公式)
:(ヘロンの公式)

- また、
 とすると、
とすると、
- 内接円の半径を
 とすると、三角形の面積
とすると、三角形の面積 
- 従って、

- 一辺のながさ
 の正三角形の面積
の正三角形の面積  :
:

 直交対角線四角形
直交対角線四角形
 凧形
凧形
- 四角形
- 縦のながさ
 、横のながさ
、横のながさ  の長方形の面積
の長方形の面積  :
:

- 一辺のながさ
 の正方形の面積
の正方形の面積  :
:

- 底辺のながさ
 、高さ
、高さ  の平行四辺形の面積
の平行四辺形の面積  :
:

- 上底のながさ
 、下底のながさ
、下底のながさ  、高さ
、高さ  の台形の面積
の台形の面積  :
:

- 対角線のながさ
 、もう一つの対角線のながさ
、もう一つの対角線のながさ  でそれらが直行する四角形(直交対角線四角形 ⊃ 凧形・菱形・正方形)の面積
でそれらが直行する四角形(直交対角線四角形 ⊃ 凧形・菱形・正方形)の面積  :
:

- 四辺の長さが
 で円に内接する四角形の面積
で円に内接する四角形の面積 :(ブラーマグプタの公式)
:(ブラーマグプタの公式)

- また、
 とすると、
とすると、
- 正多角形
- 一辺のながさ
 の正
の正 角形の面積
角形の面積  :
:

- 円と扇形
- 半径
 の円の面積
の円の面積  :
:

- 半径
 、中心角
、中心角 (度)の扇形の面積
(度)の扇形の面積 :
:

- 半径
 、中心角 θ(rad) の扇形の面積
、中心角 θ(rad) の扇形の面積  :
:

- 半径
 、弧の長さ
、弧の長さ の扇形の面積
の扇形の面積  :
:

解説はこちらのページをご覧ください
- 縦のながさ
 、横のながさ
、横のながさ  、高さ
、高さ  の直方体の表面積
の直方体の表面積  :
:

- 底面積
 :
:

- 側面積
 :
:

- 一辺のながさ
 の立方体の表面積
の立方体の表面積  :
:

- 底面の周の長さ
 、高さ
、高さ  の柱体の側面積
の柱体の側面積  :
:

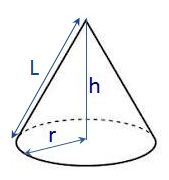 円錐
円錐
- 円錐
- 底面が半径
 、母線
、母線  の円錐:
の円錐:
- 側面積

- 表面積 = 側面積 + 底面積

- 底面が半径
 、高さ
、高さ  の円錐:
の円錐:
- 母線

- 側面積

- 表面積 = 側面積 + 底面積

 3直角四面体
3直角四面体
- 直角三角錐(3直角四面体)
- 三角錐
 において,1つの頂点
において,1つの頂点 に集まる3つの角
に集まる3つの角  ,
,  ,
,  がいずれも直角である三角錐
がいずれも直角である三角錐
- 以下、
 とする。
とする。
- 頂点
 から、
から、 に下した垂線の長さ
に下した垂線の長さ ;
;

 の面積
の面積 ;
;

- ド・グアの定理(通称:四平方の定理)
- 半径
 の球の表面積
の球の表面積 :
:

 青で示された部分が球冠の一例である。
青で示された部分が球冠の一例である。
- 球冠(平面により切断された球の一部)の曲面部の表面積
 :
:
- 関係する諸数値を以下のものとする(右図参照)。
- 球の半径

- 球冠の底の半径

- 球冠の高さ

- 球の中心から球冠の頂点(極)までの線と球冠の底を形作る円板の端との間の極角

 と
と  を用いて、
を用いて、

 と
と  を用いて、
を用いて、

 と
と  を用いて、
を用いて、

 球台
球台
- 球台(球を1対の平行な平面で切断した立体/先端が切り取られた球冠)の曲面部(球帯)の表面積
 :
:
- 関係する諸数値を以下のものとする(右図参照)。
- もとの球の半径

- 球台の底の半径

- 球台の高さ(2つの平行な底面間の距離)

 と
と  を用いて、
を用いて、

 と
と  を用いて、
を用いて、
- 球を切断する平行な2平面の外に球の中心がある場合
 (ただし、
(ただし、 )
)
- 球を切断する平行な2平面の間に球の中心がある場合

 円環体・トーラス
円環体・トーラス
- 半径
 の円を、円の中心からの距離
の円を、円の中心からの距離 (但し、
(但し、 ≦
≦  とする)の直線を軸として回転させた円環体(トーラス、ドーナツ型) の表面積:
とする)の直線を軸として回転させた円環体(トーラス、ドーナツ型) の表面積:

解説はこちらのページをご覧ください
 直方体
直方体
 円錐
円錐
 錐台
錐台
 くさび形
くさび形
- 縦のながさ
 、横のながさ
、横のながさ  、高さ
、高さ  の直方体の体積
の直方体の体積  :
:

- 一辺のながさ
 の立方体の体積
の立方体の体積  :
:

- 底面積
 、高さ
、高さ  の柱体の体積
の柱体の体積  :
:

- 底面積
 、高さ
、高さ  の錐体の体積
の錐体の体積  :
:

- 円錐
- 底面が半径
 、高さ
、高さ  の円錐の体積
の円錐の体積  :
:

- 底面が半径
 、母線
、母線  の円錐の体積
の円錐の体積  :
:
- 高さ


- 上底の面積
 、下底の面積
、下底の面積  、高さ
、高さ  の錐台の体積
の錐台の体積  :
:

- 特に、上底が半径
 の円、下底が半径
の円、下底が半径 の円、高さ
の円、高さ  の円錐台の体積
の円錐台の体積  :
:

- 下底が 縦のながさ
 、横のながさ
、横のながさ  の長方形、縦と平行である上辺のながさ
の長方形、縦と平行である上辺のながさ  、高さ
、高さ  のくさび形の体積
のくさび形の体積  :
:

- 一辺のながさ
 の正四面体の体積
の正四面体の体積  :
:

- 一辺のながさ
 の正八面体の体積
の正八面体の体積  :
:

- 一辺のながさ
 の正十二面体の体積
の正十二面体の体積  :
:

- 一辺のながさ
 の正二十面体の体積
の正二十面体の体積  :
:

- 球の体積
 :
:

 青で示された部分が球冠の一例である。
青で示された部分が球冠の一例である。
- 球冠(平面により切断された球の一部)の体積
 :
:
- 関係する諸数値を以下のものとする(右図参照)。
- 球の半径

- 球冠の底の半径

- 球冠の高さ

- 球の中心から球冠の頂点(極)までの線と球冠の底を形作る円板の端との間の極角

 と
と  を用いて、
を用いて、

 と
と  を用いて、
を用いて、

 と
と  を用いて、
を用いて、

 球台
球台
- 球台(球を1対の平行な平面で切断した立体/先端が切り取られた球冠)の体積
 :
:
- 関係する諸数値を以下のものとする(右図参照)。
- もとの球の半径

- 球台の底の半径

- 球台の高さ(2つの平行な底面間の距離)

-

 円環体・トーラス
円環体・トーラス
- 半径
 の円を、円の中心からの距離
の円を、円の中心からの距離 (但し、
(但し、 ≦
≦  とする)の直線を軸として回転させた円環体(トーラス、ドーナツ型) の体積:
とする)の直線を軸として回転させた円環体(トーラス、ドーナツ型) の体積:

 ベクトル
ベクトル
- 平面上または空間で大きさと向きをもつ量をベクトルという[1]。
- ベクトルが点
 から点
から点 に向かう有向線分で表されるとき,このベクトルを
に向かう有向線分で表されるとき,このベクトルを と書き,
と書き, を始点,
を始点, を終点という。
を終点という。
- ベクトルであることを示すのに、
 などと表記することもある。
などと表記することもある。
- ベクトルの大きさは、
 と表記する。
と表記する。
 と大きさが同じで向きが逆のベクトルを逆ベクトルといい、
と大きさが同じで向きが逆のベクトルを逆ベクトルといい、 と表記する。
と表記する。
- 始点終点による表記
 を
を とすると、
とすると、 となる。
となる。
- 大きさ
 のベクトルを零ベクトル(ゼロベクトル)といい、
のベクトルを零ベクトル(ゼロベクトル)といい、 と表記する。
と表記する。
- 大きさ
 のベクトルを単位ベクトルといい、しばしば、
のベクトルを単位ベクトルといい、しばしば、 と表記される。
と表記される。 の単位ベクトルは、
の単位ベクトルは、 である。
である。
- 加法
 三角形における理解
三角形における理解
 において、
において、 の終点
の終点 を始点として
を始点として を引くと、
を引くと、 となる。
となる。- これを、

- として、ベクトルの加法を定義する。
 ベクトルの加法
ベクトルの加法
- これは、ベクトル
 の終点をベクトル
の終点をベクトル の始点とし、
の始点とし、 の始点から
の始点から の終点までの有向線分を
の終点までの有向線分を と理解する方法であるが、各ベクトルの始点を一致させた平行四辺形の対角線をベクトルの和と理解する方法もある。
と理解する方法であるが、各ベクトルの始点を一致させた平行四辺形の対角線をベクトルの和と理解する方法もある。
- 以上の定義により、
 と逆ベクトル:
と逆ベクトル: の和は
の和は 、すなわち、
、すなわち、 である。
である。- 減法
 ベクトルの減法
ベクトルの減法
- 上記
 において、
において、 が成立していた。
が成立していた。
- ここで、通常の計算と同様の方法で
 を移項すると、
を移項すると、 -①
-①
- 逆ベクトルの定義から、

- (①の右辺)
 となり、①は成立し移項が可能であることが分かった。
となり、①は成立し移項が可能であることが分かった。
- 実数倍(スカラー倍)
 実数倍(スカラー倍)の例
実数倍(スカラー倍)の例
- 実数
 について、ベクトル
について、ベクトル を以下のとおり定義する。
を以下のとおり定義する。
 の時、
の時、 は、
は、 と方向が同じで、大きさが
と方向が同じで、大きさが であるベクトル。
であるベクトル。 の時、
の時、 は、
は、 と方向が逆で、大きさが
と方向が逆で、大きさが であるベクトル。
であるベクトル。 の時、
の時、 は、
は、 。
。
- 以下、それぞれ、零ベクトルではないベクトル
 について、
について、
-
 について、
について、 (
( は実数)であるとき、
は実数)であるとき、 は一次独立であるといい、
は一次独立であるといい、 ならば、
ならば、 が成立する。
が成立する。- したがって、
 が一次独立であるとき、
が一次独立であるとき、
 ならば、
ならば、 かつ
かつ である。
である。- 逆に、
 について、
について、 であるとき、
であるとき、 ならば、
ならば、 は一次独立である。
は一次独立である。
-
- 三次元空間においても、
 が同一平面上にないとき、
が同一平面上にないとき、 は一次独立であり、
は一次独立であり、
 ならば、
ならば、 が成立する。
が成立する。- 逆に、
 について、
について、 であるとき、
であるとき、 ならば、
ならば、 は一次独立であり、同一平面上にない。
は一次独立であり、同一平面上にない。
- ベクトル
 について、平面空間であれば2個の単位ベクトル
について、平面空間であれば2個の単位ベクトル 、三次元空間であれば3個の単位ベクトル
、三次元空間であれば3個の単位ベクトル を用いて以下のとおり表現できる。これを、ベクトルの成分表示といい、各々の要素を、
を用いて以下のとおり表現できる。これを、ベクトルの成分表示といい、各々の要素を、 成分、
成分、 成分、
成分、 成分という。
成分という。
- 平面ベクトル:

- 三次元空間ベクトル:

- 成分表示でのベクトル演算
- 成分表示でのベクトル演算は、各々の成分に対しておこなう
 とすると、
とすると、
- 加減算

- 実数倍(スカラー倍)

- ベクトルの大きさ

以下に挙げる公式で平面ベクトルで成り立つものは、三次元空間ベクトルでも成り立つ(平面ベクトルは、三次元空間ベクトルの  成分を
成分を としたもの)。
としたもの)。
- 位置ベクトル:
 とする時、
とする時、
- 点
 が、線分
が、線分 を
を に内分するならば、
に内分するならば、
- 特に、線分
 の中点を
の中点を とし、
とし、 とすると、
とすると、
 において、その重心
において、その重心 について、
について、 とすると、
とすると、
- 点
 が、線分
が、線分 を
を に外分するならば、
に外分するならば、
- 点
 が、2点
が、2点 を通る直線上の点とした時のベクトル方程式:
を通る直線上の点とした時のベクトル方程式: 
- 点
 が、空間上の3点
が、空間上の3点 を通る平面上の点とした時のベクトル方程式:
を通る平面上の点とした時のベクトル方程式: 
- 三角形の五心(重心、内心、傍心、外心、垂心)の位置ベクトル
 は、頂点の位置ベクトル
は、頂点の位置ベクトル  を用いて、
を用いて、
- 一般式:
 で表される。ここで
で表される。ここで  は重みである。
は重みである。
- なお、
 とし、三角形の面積を
とし、三角形の面積を とする※。
とする※。
- 重心


- 内心


- 傍心






- 外心


- 垂心


 と
と  の成す角が
の成す角が  のとき
のとき
 (内積の定義)
(内積の定義)
- 成分表示
- 平面ベクトルの場合、
 ,
,  とすると、
とすると、

- 空間ベクトルの場合、
 ,
,  とすると、
とすると、

 ,
,  のとき、
のとき、

 ,
,  , O は原点とするときの三角形 OAB の面積
, O は原点とするときの三角形 OAB の面積  :
:


 、ここで、
、ここで、 より
より 
- 与式に代入して、

- とくに、
 ,
,  とすると、
とすると、

- 二つのベクトル
 ,
,  に対し、
に対し、

- よって、

- 等号成立は、実数 k があって
 とできるときのみ。
とできるときのみ。
- ^ 広義には、多次元の要素を持つ存在(entity)を指し、本文のものは幾何ベクトル・空間ベクトルというが、初等数学においてはこの理解で足りる。












































































































































































































































































































































