大学受験数学 三角関数/公式集

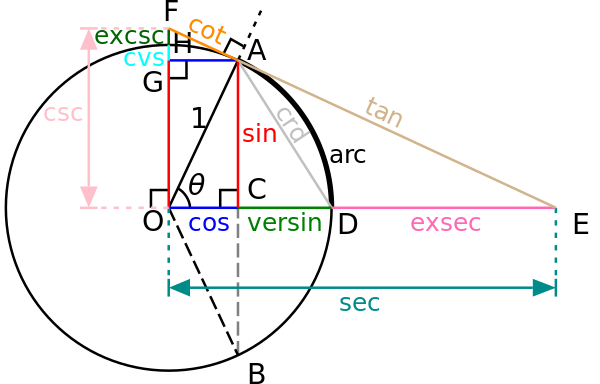
円と三角関数の関係

初等数学公式集/初等関数の性質#三角関数も参照

三角関数の定義

単位円の図。この図では角度を変数 t としてある。
（記事の本文では角度はθだが、θで描かれた単位円の図が無いので、 t の図で代用した。記事の本文と照らし合わせる場合は t をθに置き換えて読むこと。）

xy平面上に半径1の円を考える。この円を単位円（たんいえん）という。単位円は方程式 $x^{2}+y^{2}=1$ が表す図形である。

x軸の正の部分を反時計回りに角度θだけ回転させた半直線が単位円と交わる点の座標を(x,y)とするとき、次で定まる値を角度θの三角関数（さんかくかんすう）という。

$\sin \theta =y$

$\cos \theta =x$

$\tan \theta ={\frac {y}{x}}$

それぞれsinを正弦関数（せいげんかんすう、sine サイン）、cosを余弦関数（よげんかんすう、cosine コサイン）、tanを正接関数（せいせつかんすう、tangent タンジェント）という。

次に紹介するコタンジェントやセカントなどは、高校数学や大学受験では用いないのが通常だが、つぎのコタンジェントなどの関数も三角関数である。

$\cot \theta ={\frac {x}{y}}$

$\sec \theta ={\frac {1}{x}}$

$\csc \theta ={\frac {1}{y}}$

これらは余接関数（cotangent コタンジェント）、正割関数（secant セカント）、余割関数（cosecant コセカント）の頭文字をとったものである。このうち頻繁に使われるのは、$\sin \theta ,~\cos \theta ,~\tan \theta$ の3種類であり、高校数学でもsin、cos、tanの3つが標準的に使われる。以下ではサイン・コサイン・タンジェントとセカント・コセカント・コタンジェントの間には、定義から明らかに次の関係式が成り立つ。

$\cot \theta ={\frac {1}{\tan \theta }}$

$\sec \theta ={\frac {1}{\cos \theta }}$

$\csc \theta ={\frac {1}{\sin \theta }}$

サイン・コサイン・タンジェントで書かれた以下に記す公式とセカントなどの公式を組み合わせることで各種公式を導くことができるが、この節ではセカントなどの公式は省略する。

有名な三角関数の値

$\sin 0^{\circ }=0,~\cos 0^{\circ }=1,~\tan 0^{\circ }=0$

$\sin 30^{\circ }={\frac {1}{2}},~\cos 30^{\circ }={\frac {\sqrt {3}}{2}},~\tan 30^{\circ }={\frac {1}{\sqrt {3}}}$

$\sin 45^{\circ }={\frac {\sqrt {2}}{2}},~\cos 45^{\circ }={\frac {\sqrt {2}}{2}},~\tan 45^{\circ }=1$

$\sin 60^{\circ }={\frac {\sqrt {3}}{2}},~\cos 60^{\circ }={\frac {1}{2}},~\tan 60^{\circ }={\sqrt {3}}$

$\sin 90^{\circ }=1,~\cos 90^{\circ }=0$

三角関数の基本的性質

$\sin(-\theta )=-\sin \theta ,~\cos(-\theta )=\cos \theta ,~\tan(-\theta )=-\tan \theta$

$\sin(\theta +90^{\circ })=\cos \theta ,~\cos(\theta +90^{\circ })=-\sin \theta ,~\tan(\theta +90^{\circ })=-\cot \theta =-{\frac {1}{\tan \theta }}$

$\sin(90^{\circ }-\theta )=\cos \theta ,~\cos(90^{\circ }-\theta )=\sin \theta ,~\tan(90^{\circ }-\theta )=\cot \theta ={\frac {1}{\tan \theta }}$

$\sin(\theta +180^{\circ })=-\sin \theta ,~\cos(\theta +180^{\circ })=-\cos \theta ,~\tan(\theta +180^{\circ })=\tan \theta$

$\sin(180^{\circ }-\theta )=\sin \theta ,~\cos(180^{\circ }-\theta )=-\cos \theta ,~\tan(180^{\circ }-\theta )=-\tan \theta$

nを整数とするとき、

$\sin(\theta +360^{\circ }\cdot n)=\sin \theta ,~\cos(\theta +360^{\circ }\cdot n)=\cos \theta ,~\tan(\theta +180^{\circ }\cdot n)=\tan \theta$

三角関数のグラフ

正弦波（赤色）と余弦波（青色）の関数グラフ

$\sin \theta ,\cos \theta$ は波型（サインカーブ）のグラフを描く。

加法定理

いずれの式も複号同順。

$\sin(\alpha \pm \beta )=\sin \alpha \cos \beta \pm \cos \alpha \sin \beta$

$\cos(\alpha \pm \beta )=\cos \alpha \cos \beta \mp \sin \alpha \sin \beta$

$\tan(\alpha \pm \beta )={\frac {\tan \alpha \pm \tan \beta }{1\mp \tan \alpha \ \tan \beta }}$

加法定理の使用例

$\sin 15^{\circ }=\sin(45^{\circ }-30^{\circ })=\sin 45^{\circ }\cos 30^{\circ }-\cos 45^{\circ }\sin 30^{\circ }={\frac {\sqrt {2}}{2}}\cdot {\frac {\sqrt {3}}{2}}-{\frac {\sqrt {2}}{2}}\cdot {\frac {1}{2}}={\frac {{\sqrt {6}}-{\sqrt {2}}}{4}}$

$\cos 15^{\circ }=\cos(45^{\circ }-30^{\circ })=\cos 45^{\circ }\cos 30^{\circ }+\sin 45^{\circ }\sin 30^{\circ }={\frac {\sqrt {2}}{2}}\cdot {\frac {\sqrt {3}}{2}}+{\frac {\sqrt {2}}{2}}\cdot {\frac {1}{2}}={\frac {{\sqrt {6}}+{\sqrt {2}}}{4}}$

$\sin 75^{\circ }=\sin(45^{\circ }+30^{\circ })=\sin 45^{\circ }\cos 30^{\circ }+\cos 45^{\circ }\sin 30^{\circ }={\frac {\sqrt {2}}{2}}\cdot {\frac {\sqrt {3}}{2}}+{\frac {\sqrt {2}}{2}}\cdot {\frac {1}{2}}={\frac {{\sqrt {6}}+{\sqrt {2}}}{4}}$

$\cos 75^{\circ }=\cos(45^{\circ }+30^{\circ })=\cos 45^{\circ }\cos 30^{\circ }-\sin 45^{\circ }\sin 30^{\circ }={\frac {\sqrt {2}}{2}}\cdot {\frac {\sqrt {3}}{2}}-{\frac {\sqrt {2}}{2}}\cdot {\frac {1}{2}}={\frac {{\sqrt {6}}-{\sqrt {2}}}{4}}$

倍角公式

$\sin 2\alpha =2\sin \alpha \cos \alpha$

$\cos 2\alpha =\cos ^{2}\alpha -\sin ^{2}\alpha =2\cos ^{2}\alpha -1=1-2\sin ^{2}\alpha$

$\tan 2\alpha ={\frac {2\tan \alpha }{1-\tan ^{2}\alpha }}$

倍角公式の証明

加法定理から証明できる。

$\sin 2\alpha =\sin(\alpha +\alpha )=\sin \alpha \cos \alpha +\cos \alpha \sin \alpha =2\sin \alpha \cos \alpha$

$\cos 2\alpha =\cos(\alpha +\alpha )=\cos \alpha \cos \alpha -\sin \alpha \sin \alpha =\cos ^{2}\alpha -\sin ^{2}\alpha$

$\tan 2\alpha =\tan(\alpha +\alpha )={\frac {\tan \alpha +\tan \alpha }{1-\tan \alpha \ \tan \alpha }}={\frac {2\tan \alpha }{1-\tan ^{2}\alpha }}$

半角公式

$\sin ^{2}\alpha ={\frac {1}{2}}(1-\cos 2\alpha )$

$\cos ^{2}\alpha ={\frac {1}{2}}(1+\cos 2\alpha )$

$\tan ^{2}\alpha ={\frac {1-\cos 2\alpha }{1+\cos 2\alpha }}$

また、2乗が現れない次の公式もあるが、高校ではあまり扱われない。

$\tan \alpha ={\frac {\sin 2\alpha }{1+\cos 2\alpha }}={\frac {1-\cos 2\alpha }{\sin 2\alpha }}$

半角公式の証明

$\cos 2\alpha =1-2\sin ^{2}\alpha$
∴ $2\sin ^{2}\alpha =1-\cos 2\alpha$
∴ $\sin ^{2}\alpha ={\frac {1}{2}}(1-\cos 2\alpha )$

$\cos 2\alpha =2\cos ^{2}\alpha -1$
∴ $-2\cos ^{2}\alpha =-1-\cos 2\alpha$
∴ $\cos ^{2}\alpha ={\frac {1}{2}}(1+\cos 2\alpha )$

この2つより

$\tan ^{2}\alpha ={\frac {\sin ^{2}\alpha }{\cos ^{2}\alpha }}={\frac {{\frac {1}{2}}(1-\cos 2\alpha )}{{\frac {1}{2}}(1+\cos 2\alpha )}}={\frac {1-\cos 2\alpha }{1+\cos 2\alpha }}$

がいえる。通常は以上の3つを示しておけばよい。

さて、

$\tan ^{2}\alpha ={\frac {1-\cos 2\alpha }{1+\cos 2\alpha }}={\frac {(1-\cos 2\alpha )(1+\cos 2\alpha )}{(1+\cos 2\alpha )(1+\cos 2\alpha )}}={\frac {1-\cos ^{2}2\alpha }{{(1+\cos 2\alpha )}^{2}}}={\frac {\sin ^{2}2\alpha }{{(1+\cos 2\alpha )}^{2}}}$

と変形し、両端の平方根をとれば $\tan \alpha =\pm {\frac {\sin 2\alpha }{1+\cos 2\alpha }}$ ……(*)であるが、ここで値の正負を調べる。

• 分子 $\sin 2\alpha$ と $\tan \alpha$ の正負は常に一致する。
• 分母 $1+\cos 2\alpha$ は常に0か正の値をとる。0になるのは $2\alpha =\pi +2n\pi$ 即ち $\alpha ={\frac {\pi }{2}}+n\pi$ のときであるが、これは tan の定義されない地点と一致するので問題はない。

よって(*)の複号は常に正号が成り立つことが分かる。

次に

$\tan ^{2}\alpha ={\frac {1-\cos 2\alpha }{1+\cos 2\alpha }}={\frac {(1-\cos 2\alpha )(1-\cos 2\alpha )}{(1+\cos 2\alpha )(1-\cos 2\alpha )}}={\frac {{(1-\cos 2\alpha )}^{2}}{1-\cos ^{2}2\alpha }}={\frac {{(1-\cos 2\alpha )}^{2}}{\sin ^{2}2\alpha }}$

と変形し、両端の平方根をとれば $\tan \alpha =\pm {\frac {1-\cos 2\alpha }{\sin 2\alpha }}$ ……(**)であるが、ここで値の正負を調べる。同様の検討をすれば(**)の複号は常に正号が成り立つことがわかる。ただし、$\alpha =n\pi$ のときは左辺が定義できるにもかかわらず、右辺は分母子ともに0になるため定義できない（ただし、この地点での極限を議論することはできる）。ちなみに、逆数をとった ${\frac {1}{\tan \alpha }}=\pm {\frac {\sin 2\alpha }{1-\cos 2\alpha }}$ ……(**)' にはそのような地点はなくすんなりと検討できる。

半角公式の使用例

半角公式はしばしば次数を下げるために用いられる。たとえば、

$\int \sin ^{2}x\,dx=\int {\frac {1}{2}}(1-\cos 2x)\,dx={\frac {1}{2}}\left(x-{\frac {\sin 2x}{2}}\right)+C={\frac {1}{4}}(2x-\sin 2x)+C$

和積変換公式

$\sin \alpha +\sin \beta =2\sin {\frac {\alpha +\beta }{2}}\cos {\frac {\alpha -\beta }{2}}$

$\sin \alpha -\sin \beta =2\cos {\frac {\alpha +\beta }{2}}\sin {\frac {\alpha -\beta }{2}}$

$\cos \alpha +\cos \beta =2\cos {\frac {\alpha +\beta }{2}}\cos {\frac {\alpha -\beta }{2}}$

$\cos \alpha -\cos \beta =-2\sin {\frac {\alpha +\beta }{2}}\sin {\frac {\alpha -\beta }{2}}$

和積変換公式の証明

$\alpha +\beta =x,~\alpha -\beta =y$ とおく。すると $\alpha ={\frac {x+y}{2}},~\beta ={\frac {x-y}{2}}$ と表せる。

sin の加法定理より

$\sin \alpha +\sin \beta =\sin \left({\frac {x}{2}}+{\frac {y}{2}}\right)+\sin \left({\frac {x}{2}}-{\frac {y}{2}}\right)$
$=\left(\sin {\frac {x}{2}}\cos {\frac {y}{2}}+\cos {\frac {x}{2}}\sin {\frac {y}{2}}\right)+\left(\sin {\frac {x}{2}}\cos {\frac {y}{2}}-\cos {\frac {x}{2}}\sin {\frac {y}{2}}\right)$
$=2\sin {\frac {x}{2}}\cos {\frac {y}{2}}$
$=2\sin {\frac {\alpha +\beta }{2}}\cos {\frac {\alpha -\beta }{2}}$

他の3つも同様の方法で示せる。

積和変換公式

積和変換公式は次数を下げるために用いられる。

☆のついた公式は相互に書き換えができる。

$\sin \alpha \ \sin \beta =-{\frac {1}{2}}\{\cos(\alpha +\beta )-\cos(\alpha -\beta )\}$

☆ $\sin \alpha \ \cos \beta ={\frac {1}{2}}\{\sin(\alpha +\beta )+\sin(\alpha -\beta )\}$

☆ $\cos \alpha \ \sin \beta ={\frac {1}{2}}\{\sin(\alpha +\beta )-\sin(\alpha -\beta )\}$

$\cos \alpha \ \cos \beta ={\frac {1}{2}}\{\cos(\alpha +\beta )+\cos(\alpha -\beta )\}$

積和変換公式の証明

天下り的だが、右辺から左辺へと変形すれば容易に証明される。

三倍角の公式

$\sin 3\alpha =-4\sin ^{3}\alpha +3\sin \alpha$

$\cos 3\alpha =4\cos ^{3}\alpha -3\cos \alpha$

三倍角の公式の証明

$\sin 3\alpha =\sin(\alpha +2\alpha )$
$=\sin \alpha \cos 2\alpha +\cos \alpha \sin 2\alpha$
$=\sin \alpha (1-2\sin ^{2}\alpha )+\cos \alpha (2\sin \alpha \cos \alpha )$
$=\sin \alpha -2\sin ^{3}\alpha +2\sin \alpha \cos ^{2}\alpha$
$=\sin \alpha -2\sin ^{3}\alpha +2\sin \alpha (1-\sin ^{2}\alpha )$
$=3\sin \alpha -4\sin ^{3}\alpha$

$\cos 3\alpha =\cos(\alpha +2\alpha )$
$=\cos \alpha \cos 2\alpha -\sin \alpha \sin 2\alpha$
$=\cos \alpha (2\cos ^{2}\alpha -1)-\sin \alpha (2\sin \alpha \cos \alpha )$
$=2\cos ^{3}\alpha -\cos \alpha -2\sin ^{2}\alpha \cos \alpha$
$=2\cos ^{3}\alpha -\cos \alpha -2(1-\cos ^{2}\alpha )\cos \alpha$
$=4\cos ^{3}\alpha -3\cos \alpha$