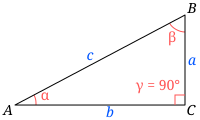大学受験数学 三角関数/公式集も参照








 (ピタゴラスの基本三角公式)
(ピタゴラスの基本三角公式)


-
- 鋭角における三角比の相互関係(三角比のいずれかが有理数で表されている場合に有用)
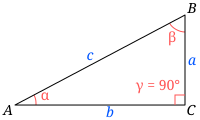
 であるとき。
であるとき。  ,
, 
 であるとき。
であるとき。  ,
, 
 であるとき。
であるとき。  ,
, 















証明は高等学校数学II/三角関数#加法定理を参照



(すべて複号同順)


-

-



-

-

-
- なお、余角の公式から、

-

-

加法定理で、 として、
として、



 ← 倍角の公式より、
← 倍角の公式より、
-
 ← 倍角の公式より、
← 倍角の公式より、
-

-

-
- (拡張)
 とするとき、
とするとき、
 ←
←  を
を について解く。
について解く。 ←
←  に
に  を代入する。
を代入する。




-
- 余角の公式より、等式:
 が成立する。
が成立する。
-
- ここで、
 とおくと、
とおくと、 となり、二倍角の公式及び三倍角の公式から、
となり、二倍角の公式及び三倍角の公式から、 。
。
-
- さらに、
 とおいて、方程式:
とおいて、方程式: を得る。
を得る。
-
- これを解いて、
 。
。 であるので、
であるので、 、従って、
、従って、
-



-
 (計算過程・有理化は略)
(計算過程・有理化は略)-
-

-
- 余角の公式より、等式:

 が成立する。
が成立する。
-
 ,
,  ,
, 
-
-
- ※
 の正弦・余弦の値を元に、
の正弦・余弦の値を元に、 の三角比の値を求めることができる(参考参照)。
の三角比の値を求めることができる(参考参照)。









- ただし、


- ただし、

覚え方
位相を  すると微分になると覚えましょう。
すると微分になると覚えましょう。 の三角関数も2階微分としてすぐに導出できます。
の三角関数も2階微分としてすぐに導出できます。 の三角関数は積分として覚えられます。また、点
の三角関数は積分として覚えられます。また、点  を
を  回転した点
回転した点  は原点を中心に点対称移動した点
は原点を中心に点対称移動した点  であることからも、
であることからも、 の三角関数を導出できます。
の三角関数を導出できます。
 の三角関数は、点
の三角関数は、点  を
を  軸で線対称移動移動した点が
軸で線対称移動移動した点が  であることから導出できます。
であることから導出できます。
加法定理は「咲いたコスモスコスモス咲いた」、「コスモスコスモス咲いた咲いた」という語呂合せがあります。
 の倍角の公式
の倍角の公式  は
は  という形を覚えて
という形を覚えて  は符号が
は符号が  、1 の符号はその逆と覚えます。
、1 の符号はその逆と覚えます。
2乗の三角関数  は、
は、 という形を覚えて、
という形を覚えて、  は符号が
は符号が と考えます。
と考えます。
正弦合成では、Oを原点とするxy平面上に点P(a, b)をとったときの線分OPの長さがサインの係数、直線OPの傾き が
が の値 と考えます。
の値 と考えます。
余弦合成では、Oを原点とするxy平面上に点Q(b, a)をとったときの線分OQの長さがコサインの係数、直線OQの傾き が
が の値 と考えます。
の値 と考えます。
以下、この節内では a, b ,c は実数とする。






以下、 かつ
かつ  とし、また対数の真数として表れるものはすべて正とする。
とし、また対数の真数として表れるものはすべて正とする。
- 対数の定義

 ,
, 




- 特に
 ,
,