小学校算数/4学年
大きな数
[編集]3年生まででは、千万の位についてまで学びましたが、それより大きい数について学びましょう。
億(おく)
[編集]次の数字を読んでみましょう。 どんな数でも、10倍すると、位が1つ上がり、右はしに0を1こつけた数になりますね。千万を10倍した数を、 一億 (いちおく)といいます。 次の数を読みましょう。 128734906
答えは、
100000000が 1億 です。 1 のうしろに 0 が 8個 あります。
一億の次は、十億、百億、千億です。
兆(ちょう)
[編集]千億の十倍は、何かを考えてみましょう。千億を10倍すると、位がひとつ上がり、 一兆(いっちょう)という数になります。億の位の次は、兆の位になるのです。
1000000000000 が 1兆 です。 1 のうしろに 0 が 12個 あります。
一兆の次は、十兆、百兆、千兆です。
整数を作ろう
[編集]0、1、2、3、4、5、6、7、8、9の10この数を使って、一番大きい整数を作りましょう。一番大きい整数を作るには、大きい数からじゅんにならべましょう。答えは、9876543210です。
0、1、2、3、4、5、6、7、8の9つの数を使って、一番小さい整数を作りましょう。しかし、「012345678」ではありません。0は、一番左はしにつけることはできません。そのため、0は、左から2番目につけて、答えは、102345678となります。
兆から先のくらい
[編集]1兆に1000をかけた数は 1000兆(せんちょう) です。 1兆に10000をかけた数は 1京(いっけい) と いいます。
10000000000000000 が 1京 です。1京は 1 のうしろに 0 が 16個 あります。
小学校の算数では、ふつうは 1000兆の位までの数字しか、つかいません。
さらにそのさきは、つぎのようになっています。
- 1の後ろに0が20個で 1垓(1がい) です。
- 1の後ろに0が24個で 1𥝱(1じょ) です。
- 1の後ろに0が28個で 1穣(1じょう) です。
- 1の後ろに0が32個で 1溝(1こう) です。
- 1の後ろに0が36個で 1澗(1かん) です。
- 1の後ろに0が40個で 1正(1せい) です。
- 1の後ろに0が44個で 1載(1さい) です。
- 1の後ろに0が48個で 1極(1ごく) です。
- 1の後ろに0が52個は 1恒河沙(1ごうがしゃ) です。
- 1の後ろに0が56個で 1阿僧祇(1あそうぎ) です。
- 1の後ろに0が60個で 1那由他(1なゆた) です。
- 1の後ろに0が64個で 1不可思議(1ふかしぎ) です。
- 1の後ろに0が68個で 無量大数(むりょうたいすう) です。
小学校の算数の計算では、ふつうは、「垓」や「𥝱」や「無量大数」などの大きな位(くらい)は、使いません。
小学校の算数では、億(おく)や兆(ちょう)の使い方を、おぼえてください。
わり算の筆算
[編集]この節は書きかけです。この節を編集してくれる方を心からお待ちしています。
- たてる
- かける
- ひく
- おろす
計算のきまり
[編集]今までに、たし算・ひき算・かけ算・わり算の4つを勉強しました。ここでは、それらがまざった式の計算について学習しましょう。
このような計算は、下のようなじゅんばんで計算するのがきまりです。
- かっこが式にある場合はかっこの中を先に計算
- かけ算・わり算
- たし算・ひき算
また、同じじゅんいにあるものは式の左にあるものから計算することになっています。 では、次の計算をしてみましょう。
この式にはかっこがあるのでかっこの中身を先に計算します。またかっこの中にある式の計算のじゅんばんも上にある通りです。まずはかっこの中にあるわり算から計算します。 なので、このような式になります。
まだ かっこの中には 式があるので 次はその部分を 計算します。 です。 このように かっこの 中身を 全て 計算すること を かっこを外す と言います。
これで かっこを 外すことが できました。 たし算 と かけ算 が のこっていますが 上のじゅんばんを 見ると つぎ に やるのは かけ算 です。
左から 計算 するので、 まずは を計算します。
つぎはさっき計算しなかった かけ算 の を 計算します。
これで かけ算が すべて終わりました。 のこり は たし算 ですが、 これも 同じように 左から 計算します。です。
最後に のこった式を 計算します。 すると 答えの 21が 出てきました。
たし算・ひき算・かけ算・わり算が まじった式を計算する場合は このように行います。
「4つの4」とは、4つの4と計算記号を使って いろいろな数を作るパズルです。
たとえば、答えが0になる式には、
などがあります。
このようにして、答えが1から9になる式を作ってみましょう。
考えてみた後、答えを見てください。 4つの4の答え
小数
[編集]この節は書きかけです。この節を編集してくれる方を心からお待ちしています。
みなさんは、「1.5」や「0.3」のような数を見たことをありますか?このように、「.」がつく数について学習しましょう。
0.1 や 0.5 や 4.8 のような数を 小数 (しょうすう)といいます。真ん中の「.」を、 小数点(しょうすうてん) といいます。小数点の右の数字を「小数第1位」(しょうすう だい いちい)や「の位」(じゅうぶんのいちのくらい)と、いいます。
0 や 1 や 10 などのような数を、つまり 小数では ない 数を、 整数 (せいすう)と いいます。
たとえば 3563 は整数です。たとえば 100.01 は整数では、ありません。
小数×整数
[編集]小数÷整数
[編集]分数
[編集]分数は例えば例えば(にぶんのいち)や(いちとさんぶんのに)があります。
分数の種類
[編集]分数の種類には、大きく分けて3通りあります。
- 真分数(しんぶんすう)
- 分母よりも分子の数が小さい分数です。
- たとえば とか とか のようなものです。
- 仮分数(かぶんすう)
- 分母と分子の数字が同じであるか、分子の数が分母より大きい分数のことです。
- たとえば とか とか のようなものがあります。
- 帯分数(たいぶんすう)
- 整数と真分数の和を表します。真分数の左に整数がついたものです。
- たとえば () とか とか のようなものがあります。
分数のたし算とひき算
[編集]分母が同じ計算
[編集]- 分数の計算の考え方
を計算しましょう。
分数の足し算は、つぎのように、考えて、計算します。
つぎの図を、見てください。
分母が同じ場合の、分数の、足し算 :
よって、
- (=)
です。
- 分数の引き算の例 :
を計算すると、どうでしょうか。
よって、
です。
次のたし算の問題を解いてみましょう。
- ジュースがパックに、L、ペットボトルにL入っています。合わせて何リットルありますか。
式はとなります。
計算のしかたを考えてみましょう。
はの3こ分、はの4こ分です。
したがって、が(3+4=7) より7こ分あります。
が7こ集まると、となります。
なので、となります。答えはLです。
答えをLと
次のひき算の問題を解いてみましょう。
- ジュースがLあります。L飲むと、残りは何Lですか。
式はとなります。
計算のしかたを考えてみましょう。
はが7個、はが2こ分です。
したがって、が(7-2=5)より5こ分あります。
が5こ集まると、となります。
なので、となります。答えはLです。
分母が違う計算
[編集]この節は書きかけです。この節を編集してくれる方を心からお待ちしています。
数のはんい
[編集]数のはんいの表し方には「以上」「以下」「未満」があります。
以上
[編集]- その数と
等 しいか、その数よりも大きいことを以上 といいます。 - たとえば、「5以上」といえば、5, 6, 7, 8, 9...のように、5と5より大きい数をさします。
以下
[編集]- その数と
等 しいか、その数よりも小さいことを以下 といいます。 - たとえば、「5以下」といえば、5, 4, 3, 2, 1...のように、5と5より小さい数をさします。
未満
[編集]- ある数よりも小さい場合、その数の 未満(みまん) である、というふうに言います。
- たとえば、「5未満」といえば、5は数えずに4, 3, 2, 1...のように、5より小さい数をさします。
がい数
[編集]東京 23区の人口は 9272740人 です(2015(平成 27)年10月1日の国勢調査 による)
この数は人口をくわしく知りたい時には
そこで、数を分かりやすくするために およその数 について考えてみましょう。
およその数のことを がい数 といいます。
切り上げ(きりあげ)と 切り捨て(きりすて)
[編集]ある位を見た時に、 その数字の1つ上の位に1を足して、それ以下の数字を全て0にする ことを 切り上げ (きりあげ)といいます。
また、逆に その数字の位以下の数字を全て0にする ことを 切り捨て (きりすて)といいます。
では東京23区の人口を一万の位で切り上げたり切り捨ててみましょう。一万の位で切り上げる場合は1つ上の位である十万の位に1を足して、一万の位以下の全ての位を0にします。例えばこの場合は 9300000人 となります。
同じように一万の位で切り捨ててみると、一万の位以下の全ての位を0にすればいいので、 9200000人 となります。
四捨五入
[編集]ある位を見た時に、 その数字が0~4の場合は切り捨てて、5~9の場合は切り上げる ことを 四捨五入 (ししゃ ごにゅう)といいます。また、概数(がいすう)と言われるものは ほとんどの場合は 四捨五入のことを指します。
では、東京23区の人口を、千の位と一万の位で四捨五入してみましょう。
千の位の数字は「2」です。つまり、この場合は切り捨てればよいのです。すると、 9270000人 となります。
また、一万の位の数字は「7」です。つまり、この場合は切り上げればよいのです。すると、 9300000人 となります。
四捨五入の位
[編集]問題では「一万の位で四捨五入」や「千の位まで四捨五入」、「上から1けたまでのがい数」という書かれ方をよくします。この時、四捨五入をする位が少し違ってきます。
例えば、「一万の位で四捨五入」の「で」の場合、その位(ここでは一万の位)で四捨五入をします。
一方で、「千の位まで四捨五入」の「まで」の場合、その1つ下の位(ここでは百の位)で四捨五入をします。
さらに、「上から1けたまでのがい数」という場合は指定された1つ下の位(ここでは上から2けた目の位)で四捨五入をします。
- まとめ
「で」とついている場合は指定された位で四捨五入します。また「まで」となっている場合は指定された位の1つ下の位で四捨五入します。
がい算
[編集]四捨五入やがい数をつかって、おおよその計算をすることを がい算 といいます。
たとえば
- 4187603 + 2705626 = 6893229
を、十万未満の位は、四捨五入で計算した場合、
- 4200000 + 2700000 = 6900000
に、なります。だいたい同じ数字になりましたね。
これはがい算を、したことになります。
がい算は、べつに足し算だけでは、ありません。引き算でもかけ算でもわり算でも、四捨五入や切り上げ・切り捨てなどをしてがい数を使って計算していればがい算です。
図形
[編集]角とその大きさ
[編集]
角の大きさは、
- 角の大きさの
単位 は「」とかき、「度 」とよみます。一回転したときの角の大きさはです。 - の角の大きさを直角といいます。
- 三角じょうぎの角度
面積
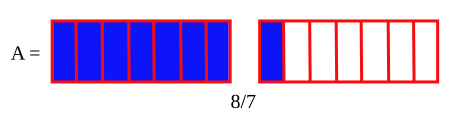
[編集]
そこで、1辺が1cmの正方形の面積を1cm2(1平方センチメートル)とします。 面積は、1辺1cmの正方形がいくつ分かで表します。
たて4cm、よこ5cmの長方形の面積を考えてみましょう。 1辺が1cmの正方形がたてに4つ、よこに5つしきつめられているので、
- より、20cm2です。
このように、長方形の面積は、 たて×横 で、
垂直・平行と四角形
[編集]垂直と平行
[編集]垂直
[編集]2本の直線でできる角が直角であるとき、その2本の直線は

平行
[編集]2本の直線が1本の直線に垂直なとき、その2本の直線は
左の図で2本の黒の直線は平行になっています。また、平行な2本の直線は交わりません。


いろいろな四角形
[編集]台形
[編集]向かい合った1組の
左の図で、上の辺と下の辺は平行になっています。
平行四辺形
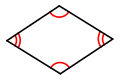
[編集]向かい合った2組の辺が平行な四角形を、
平行四辺形の、向かい合った辺の長さは等しくなっています。
また、向かい合った角の大きさも等しくなっています。となり合った角の角度をたすと、180°になります。

ひし形
[編集]4つの辺の長さがみな等しい四角形を、ひし形(ひしがた)といいます。
ひし形の、向かい合った辺は平行で、向かい合った角の大きさは等しくなっています(右の図を見てください)。

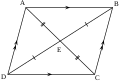
四角形の対角線
[編集]向かい合った頂点をつないだ直線を、対角線(たいかくせん)といいます。左の図では、ABが対角線になっています。
四角形の対角線の数は2本です。
直方体と立方体
[編集]

- 直方体
- ふでばこのような同じ大きさの長方形でかこまれた立体を 直方体 (ちょくほうたい)といいます。
- 直方体
立方体や直方体は、正方形や長方形で、かこまれています。
立方体や直方体をかこんでいる、図形のことを
たとえば立方体の面は6個あって、6個とも、面は、すべて、正方形です。
直方体には、
直方体には、辺が 12本 あります。(数えてみてください。)

直方体の展開図は11種類あります。

- 立方体
- さいころのような、すべての面が同じ大きさの正方形である立体を 立方体 (りっぽうたい)と言います。
- 立方体
- 見取図
- 立体全体のおおよその形がわかるように書いた図を
見取図 といいます。
- 展開図
立体を辺にそって、つながったまま、切り開いたものを 展開図(てんかいず) といいます。 立方体の展開図は、次の11種類です。
計算の答え
[編集]和
[編集]たし算の答えのことを
差
[編集]ひき算の答えのことを
積
[編集]かけ算の答えのことを
商
[編集]わり算の答えのことを
- たとえば、13÷3=4あまり1 となりますが、このときの商は4です。あまりの1は商ではありません。
折れ線グラフ
[編集]
Jは1月のこと、Fは2月のこと、Mは3月、・・・、Dは12月。
Month とは、1月や2月などの「月」のこと。
Temparature とは「温度」のこと。
右のグラフのように、数を折れ線でつないだものを
| 月 | 最高気温 | 最低気温 |
|---|---|---|
| 1月(J) | ー8 | ー14 |
| 2月(F) | ー5 | ー12 |
| 3月(M) | 0 | ー6 |
| 4月(A) | 6 | ー1 |
| 5月(M) | 10 | 3 |
| 6月(J) | 14 | 7 |
| 7月(J) | 17 | 10 |
| 8月(A) | 17 | 10 |
| 9月(S) | 13 | 5 |
| 10月(O) | 7 | ー1 |
| 11月(N) | 1 | ー7 |
| 12月(D) | ー5 | ー11 |
上の表で、0℃よりも、ひくい、氷点下の温度は、マイナス「ー」で、あらわした。
折れ線グラフにすると、かわっていくようすが、わかりやすい。
折れ線が右上がりの場合は、
折れ線が平らな場合は、増えも減りもせず、かわらない場合である。
算数ドリル
[編集]今までに習った知しきを使って、問題をもっとたくさんときたい人は、
「4年生のための算数ドリル」のページを見に行ってください。
下の「4年生のための算数ドリル」の文字をおすと、
見ているページがドリルのぺージにかわります。