小学校算数/5学年
5年生の算数では、整数、分数の計算、合同な図形、多角形などについて学習します。
整数
[編集]偶数と奇数
[編集]4年生までに、整数のことについて学びました。では、整数についてもっと深く学んでいきましょう。
2でわり切れる整数を「
なお、一の位の数が
- 0,2,4,6,8
ならばその数は偶数で、
- 1,3,5,7,9
ならばその数は奇数です。
- 問題
- 54,78,85,231は偶数ですか、奇数ですか。
- 答え
- 一の位の数に注目しましょう。
- それぞれ、
- 4,8,5,1
- なので、
- 結果は、
- 54…偶数
- 78…偶数
- 85…奇数
- 231…奇数
- となります。
倍数と約数
[編集]倍数
[編集]ある整数に整数をかけてできる数を、ある整数の
などがあります(0については考えません)。ある整数の倍数は数え切れません。
約数
[編集]ある整数をわり切ることができる整数を、ある整数の
とできるので1,2,3,4,6,12の6個あります。約数の
12の約数を調べる方法を考えてみましょう。
- まずは、積が12となる2つの整数を探す方法で調べてみましょう。
- このようなものを調べると(1との積が12になる整数、2との積が12になる整数、…と調べることができます)、
- 1と12、
- 2と6,
- 3と4
があります。
- これから、12の約数は 1,2,3,4,6,12 であることがわかります。
- (実際には、4以上との整数との積を調べる必要はありません。一度出ています。このように、一度出た整数が
再 び現 れたら終了 となります。
公倍数と公約数
[編集]2つの整数に共通している倍数を
- たとえば、12と16の倍数を書き出すと、
| 12の倍数 | 12 | 24 | 36 | 48 | 60 | 72 | 84 | 96 | 108 | 120 | 132 | 144 | 156 |
| 16の倍数 | 16 | 32 | 48 | 64 | 80 | 96 | 120 | 144 | 160 | 176 | … |
- となるので、12と16の公倍数は 48,96,144…となります。12と16の最小公倍数は 48 となります。
- また、3つの数 4と6と9 の最小公倍数について考えてみましょう。
| 4の倍数 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 |
| 6の倍数 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 |
| 9の倍数 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 | 108 |
- となるので、4と6と9の最小公倍数は36となります。
- なお、4と6の最小公倍数は12なので、12の倍数と9の倍数で考えることができます(同じように、6と9の最小公倍数である18の倍数と4の倍数を用いて考える、などの方法もあります。このように、最小公倍数は、それぞれの整数の倍数を書き出して考えることができます。
2つの整数に共通している約数を
- たとえば、12と16の公約数を書き出すと、
| 12の約数 | 12 | 6 | 4 | 3 | 2 | 1 |
| 16の倍数 | 16 | 8 | 4 | 2 | 1 |
- となるので、12と16の公約数は 1,2,4となります。12と16の最大公約数は 4 となります。
式と計算
[編集]整数と小数のしくみ
[編集]
- 10倍すると538.5、
- 100倍すると5385、
- 1000倍すると53850 と、小数点が
移 っていきます。 - このように、ある数を10倍、100倍、1000倍…にすると、小数点が右に1けた、2けた、3けた…ずつずれていきます。
また、

- にすると51.54、
- にすると5.154、
- にすると0.5154、と、小数点が
移 っていきます。 - このように、ある数をにすると、小数点が左に1けた、2けた、3けた…ずつずれていきます。
小数のかけ算、わり算
[編集]この節は書きかけです。この節を編集してくれる方を心からお待ちしています。
整数のかけ算、わり算の意味
[編集]小数のかけ算、わり算の意味
[編集]小数のかけ算とわり算も、整数の場合と同様にできます。 しかし整数と同じように計算すると矛盾します。
小数のかけ算、わり算の計算
[編集]小数 × 小数
[編集]次のかけ算の問題を解いてみましょう。
- 1mの重さが2.3kgのパイプがあります。このパイプが2.8mあったら重さは何kgですか。
式は となります。
計算のしかたを考えてみましょう。
パイプの重さを23kgと10倍にすると、求める重さも10倍になります。
パイプの長さが10倍になると、求める重さも10倍になります。
- 1mの重さが23kgのパイプ28mの重さは
1mの重さが2.3kgのパイプ2.8mの重さを出すには、この積を にすればよいので
したがって、 となります。答えは6.44kgです。
小数 ÷ 小数
[編集]次のわり算の問題を解いてみましょう。
- 6.5mの重さが7.8kgの鉄のぼうがあります。この鉄のぼう1mの重さは何kgですか。
式は となります。
計算のしかたを考えてみましょう。
同じぼうの長さを10倍にすれば、重さも10倍になります。
65mのぼうの重さは
鉄のぼう1mの重さは
したがって、 となります。答えは1.2kgです。
約分
[編集]右の図を見てください。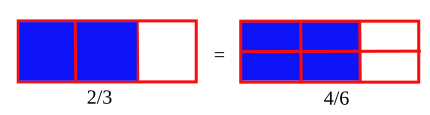
 ととが同じ大きさであることがわかるでしょう。ですから、やはになおせますね。
ととが同じ大きさであることがわかるでしょう。ですから、やはになおせますね。
ある分数の分子と分母に、同じ数をかけたりわったりしても分数の大きさは変わりません。それを使って、分数を、分母と分子ができるだけ小さい分数に、大きさを変えないでなおすことを
約分する方法には、分母と分子を分母と分子の最大公約数でわる方法があります。上のを約分してみると、4と6の最大公約数は2なので、
となります。
通分
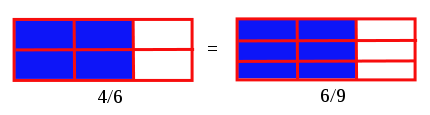
[編集]先ほどの 約分 とは逆に、たとえば、は や となおせますね。
たとえば、 は …となおすことができます。
また、 は … となおすことができます。
いま、とは それぞれ 、 になおせました。このように、2つ以上の分数を 分母が同じ大きさになるように直すことを
分数のたし算とひき算
[編集]分母がことなる分数のたし算やひき算について考えてみましょう。
では、について考えてみましょう。
分母が同じ分数のたし算はすでに学んでいます。そこで 通分 して、分母をそろえると、
となります。これを計算すると となるので、答えは です。
では、について考えましょう。 これも、先ほどと同じように通分して、
となります。上のように、答えが約分できる場合は、必ず約分します。
わり算と分数
[編集]次の問題を解いてみましょう。
- 2Lのジュースを3等分します。1人分は何Lになりますか。
式は となります。
小数で表すと となり、わりきれません。
1Lを3等分した量は、Lになります。
2Lは1Lの2つ分です。
2Lを3等分した量のうちの1つは1Lを3等分した量の2つ分であるから、 Lになります。
したがって となります。
このように、分数は、分数を使うと
整数どうしのわり算の商は、分数で表すことができます。
また、0.5と0.24を分数になおしましょう。
であるから、
であるから、
小数は、10、100などを分母とする分数になおすことができます。
5を分数になおしましょう。
整数は、1などを分母とする分数になおすことができます。
計算のきまり
[編集]次の問題を考えましょう。
●と○は全部で何個ありますか。
とを全部あわせて考えると、たてが黒4つ白3つで横が6つになるので、
の数との数をそれぞれ求めてあわせると
よって
が成り立ちます。
( )を使った式の計算には次のような法則(ほうそく)があります。
このような法則(ほうそく)を 分配法則(ぶんぱいほうそく) といいます。(小学校では、法則名は覚えなくても構いません。)
この考えを使って、くふうして暗算で計算しよう。
たし算とかけ算には、次のようなきまりがあります。
これを たし算の 交換法則(こうかん ほうそく)と言います。
これを たし算の 結合法則(けつごう ほうそく)と言います。
これを かけ算の 交換法則(こうかん ほうそく)と言います。
これを かけ算の 結合法則(けつごう ほうそく)と言います。
この考えを使って、くふうして暗算で計算しよう。
図形
[編集]合同
[編集]
2つの図形が、その図形の位置や向きをかえて、形と大きさをかえずに、重ねられるとき、その2つの図形は
多角形
[編集]
多角形 (たかくけい)とは、3本以上の線でかつそのどれもが結ばれた図形のことを言います。名前は線が3本なら 三角形 、4本なら 四角形 、5本なら 五角形(ごかくけい)、・・・というふうになります。
また、辺の長さと角の大きさが全て同じである多角形のことを 正多角形 (せいたかくけい)と言います。三角形の場合は正三角形、四角形の場合は正四角形(「正方形」(せいほうけい)というのがふつうです)、五角形の場合は正五角形・・・というふうになります。

正多角形のかきかた
[編集]正多角形は、まず円をかき、その中心の周りの角を等分することでかけます。例えば正五角形は、円をかき、その中心の周りの角を5等分して、72°ずつに区切り、区切る直線が縁と交わったところの点を結ぶことで書けます。なお、正六角形は、
図形の角
[編集]三角形の3つの角の大きさの和
[編集]三角形をかいて、3つの角をはかって和を求めてみましょう。三角形の3つの角の大きさの和は、どんな三角形でも 180°になります。
四角形の4つの角の大きさの和
[編集]四角形の4つの角の大きさの和は、どんな四角形でも 360°になります。
四角形に対角線を1本引けば、ふたつの三角形に分かれるので、2つの三角形の三角形の3つの角の大きさの和に等しくなります。
多角形の内角の和
[編集]五角形では、五角形の5つの角の大きさの和は、三角形の3つの角の大きさの和に等しくなります。

五角形の内角の和をもとめるための対角線のひきかたには、いろいろとありますが、とにかく五角形の内角の和は三角形の3つの角の大きさの和に等しくなります。
- 五角形の内角の和は 180°×(5-2)=540° より、五角形の内角の和は 540°になります。

六角形の6つの角の大きさの和をもとめるための対角線のひきかたには、いろいろとありますが、とにかく六角形の6つの角の大きさの和は、4つの三角形の3つの角の大きさの和になります。
円周の長さと円周率
[編集]円のまわりの長さを
- では、直径7cmの円の円周は何cmでしょう。
円周は曲がっているので、定規でははかれません。しかし「円周÷直径」はどの円でも同じです。これを 円周率(えんしゅうりつ) といいます。
円周率は分数で表すことはできず、また小数で表しても
- 円周÷直径=3.14
でしたから、
- 円周=直径×3.14
ですね。はじめの問題を
円と、円にぴったり入る正多角形と、円がぴったり入る正多角形をかくと、この円の周は内側の正多角形より長く、外側の正多角形よりは短くなり、これから円周率のおよその値がわかります。古代ギリシアの数学者アルキメデスは、円にぴったり入る正96角形と、円がぴったり入る正96角形を使い、円周率は
3 (=3.1408…)より大きく、3 (=3.1428…)より小さいことを発見しました。また、オランダの数学者ルドルフ(1539年~1610年)は、
正4611686018427387904角形(正2の62乗角形)を使って、円周率を小数点以下35けたまで求めました。その後も、日本の数学者 関孝和(せきたかかず)や建部賢弘(たけべかたひろ)などが円周率を研究しました。2024年現在、コンピューターを用いて、202兆1122億9000万桁以上計算されています。(正多角形の考え方ではなく、「計算結果が円周率になる式」が使われています。)今でも、円周率は日々計算されています。
面積
[編集]面積は、図形の広さを表すものです。例えば、
面積は長方形・正方形の場合は、たて×よこで表すことができました。
たとえば、たて4cm、よこ5cmの長方形の面積は、4×5=20(cm2)となります。
次の図形でも、面積は次のように求めることができます。
三角形の面積
[編集]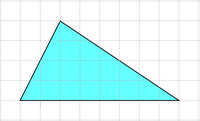


右の図1の方眼紙は1目もり1cmです。図1の三角形の面積を考えてみましょう。
- 図2のように三角形の周りにたて4cm、横8cmの面積を作ると面積の等しい直角三角形が2組できます。だから、三角形の面積はこの長方形の面積の半分になります。また、図3のように、三角形で、ある辺を
底辺 としたとき、向かい合う頂点 から底辺に垂直 に引いた直線を高さといいます。辺と高さが重なったり、高さが図形の外にきたりすることもあります。図2の長方形で、たての長さは高さ、横の長さは底辺とみることができるので、三角形の面積の公式は 底辺×高さ÷2 となります。図3のように高さが図形の外にあってもこの公式は使えます。図1の三角形の面積は より、16cm2となります。
平行四辺形の面積
[編集]

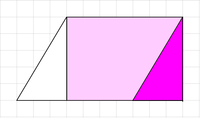

右の図1の方眼紙は1目もり1cmです。図1の平行四辺形の面積を考えてみましょう。
- 図2の位置から図3の位置に色の
濃 い三角形を移動すると、だから、三角形の面積はこの長方形の面積の半分になります。また、図4のように、平行四辺形で、ある辺を底辺 としたとき、底辺とそれに向かい合う辺のはばを 高さ といいます。図2の平行四辺形で、たての長さは高さ、横の長さは底辺とみることができるので、平行四辺形の面積の公式は 底辺×高さ となります。高さが図形の外にあってもこの公式は使えます。図1の平行四辺形の面積は より、35cm2となります。
台形とひし形の面積
[編集]台形
[編集]


図1の台形の面積を考えてみましょう。
- 図2のように、この台形を2つならべると平行四辺形ができます。台形の面積はこの平行四辺形の半分です。図3のように、台形にで、平行な2本の辺をそれぞれ
上底 、下底 といいます。この平行四辺形で、底辺は(上底+下底)で、高さはもとの台形の高さと同じなので面積は (上底+下底)×高さ となります。台形の面積はこの半分なので、台形の面積の公式は (上底+下底)×高さ÷2 となります。
ひし形
[編集]


図1のひし形の面積を考えてみましょう。
- 図2のように、ひし形の周りに長方形を作ります。ひし形の面積は長方形の面積のちょうど半分です。長方形のたてと横はそれぞれひし形の対角線となっています。ですから、図3のように、ひし形の面積の公式は 対角線×対角線÷2 となります。
体積
[編集]2年生では、「かさ」や「L」などの単位について、ならいました。
1L=1000cm3である。
立体の、空間での大きさ(今までに習った「かさ」のこと)を 体積 (たいせき) といいます。
面積では、縦(たて)と横(よこ)が 1cm の正方形の面積のことを 1cm2 と いいました。
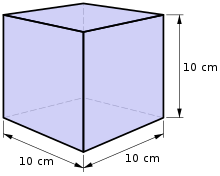
体積では、縦(たて) と 横(よこ) と 高さ(たかさ) が 1cm の 立方体 の 体積 を 1cm3 と 書き 、「 1 立方(りっぽう) センチメートル」といいます。
体積は、縦と 横と 高さが 1cm の 立方体 の 体積(1cm3)が、いくつ分かで表します。
直方体(ちょくほうたい) は 長方形 が たくさん 積み 重なった もの 、 立方体は 正方形 が たくさん 積み 重なったもの と 考えてみると、体積は たて×横× 高さ の式で 求めることができます。
立方体(りっぽうたい) は 全ての辺の長さが同じなので、高さも1辺の長さになります。また、底面の面積は今までどおり 縦×横 の式で計算できます。
つまり、
- 直方体の体積は たて×横×高さ
- 立方体の体積は 1辺×1辺×1辺
で求めることができます。
下の問題を見てみましょう。
- 縦2cm 、 横3cm 、 高さ6cm の 直方体の 体積を もとめましょう。
という問題があります。
直方体の体積は 縦×横×高さ なので、2×3×6=36(cm3)と求められます。
- 立方メートル
一辺が1mの立方体の体積を1立方メートル(いち りっぽうメートル)と言い 1m3 と書きます。1立方メートルを立方センチメートルで書いたとすると、1mは100cmですから、1m3 は
- 1m3 = 100cm × 100cm × 100cm = 1000000 cm3
です。(一立方メートルは、百万立方センチメートル)
- 内のりと容積
コップや水槽(すいそう)、プールなど、水などの液体(えきたい)をいれる容器(ようき)について、容器の内部の長さを内(うち)のりといい、その容器に入りきる液体の体積を 容積(ようせき) といいます。
容積の単位(たんい)は、体積と同じようにLやdLや立方cm3や立方m3などを、つかいます。
なお、1Lは 1000cm3 です。つまり
- 1L=1000cm3
です。
1dLは 100cm3 です。つまり
- 1dL=100cm3
です。
1mLは 1cm3 です。つまり
- 1mL = 1cm3
です。
角柱と円柱
[編集]角柱と円柱
[編集]- 三角柱
三角柱には面が、5個、あります。三角柱の面のうち、2個は三角形です。三角柱の面のうち、3個は四角形です。
三角柱には、頂点が 6個 あります。(数えてみてください。)
三角柱には、辺が 9本 あります。(数えてみてください。)
三角柱の上下の2つの三角形の面を 底面(ていめん) と言います。
底面の面積のことを 底面積(ていめんせき) と言います。
三角柱の底面積は、底面の円の面積とおなじです。
上側の面も、「底」面というのは変だと思うかもしれませんが、慣習(かんしゅう)で、こう呼びます。
三角柱の、2つの三角形である底面のあいだのきょりを、三角柱の 高さ といいます。
三角柱の、展開すると四角形になる部分の面を 側面(そくめん) と言います。
側面の面積のことを 側面積(そくめんせき) と言います。
- 円柱

この図では、hが「円柱の高さ」です。

- トイレットペーパーの しん の ような 同じ大きさの円 が 積み重なってできた立体を 円柱 (えんちゅう)と言います。
円柱には面が3個あります。
円柱の面のうち2個は円です。
円柱の上下の2つの円の面を 底面(ていめん) と言います。
円柱の、2つの円である底面の中心を結んだきょりを、円柱の 高さ といいます。
円柱の、展開すると四角形になる部分の面を 側面(そくめん) と言います。
展開図をみると、側面積の縦の長さを「円柱の高さ」にとった場合は、側面積の横の長さは、底面の円周です。
です。
数量関係
[編集]単位量あたりの大きさ
[編集]単位量あたりの量
[編集]サッカーボールを買うために、2つの店 A店とB店に行きました。
- A店では 「サッカーボール2つ3000円」で売っており、
- B店では「サッカーボール5つ8000円」で売っていました。
- どちらが安いといえるでしょうか。
ここでは、サッカーボールの数が
一方、「サッカーボール1つで1200円」と、「サッカーボール1つで1300円」とであれば、
「サッカーボール1つで1200円」の方が安いということはすぐ分かります。
つまり、サッカーボールの数が違うときは、サッカーボール1つあたりの
このように、「~1つあたり」のようなものを、単位あたりの量といいます。「単位」というのは、「
- (注意)「
豚 肉100gあたり130円」などというように、1を基準としないものもあります。
- A店でのサッカーボールの1個あたりの値段は、円で、
- B店でのサッカーボールの1個あたりの値段は、円で、
1個あたりの値段で比べれば、A店のほうが安いといえます。
(練習問題)
- サッカーボール5個で6000円のとき、サッカーボール1個あたりの値段を求めましょう。
- (円)
- サッカーボール1個あたり1000円のとき、3個買うと、全部でいくらですか。
- (円)
- 1.5Lのジュースが、180円でした。このジュース1Lあたりの値段を求めましょう。
- (円)
- 1Lあたり130円のジュースを2.3L買いました。全部でいくらですか。
- (円)
- 1.5Lのジュースが、200円でした。1円あたりジュースを何L買えるでしょう。
- (L)
人口密度
[編集]1km2あたりの人口を
- 東京都の人口:1351万人、面積:2191km2
- 高知県の人口:72万人、面積:7104km2 (2015年の
国政調査 データ・改)
- 東京都:1351000÷2191=6166.13… より、約6200人、
- 高知県:720000÷7104=101.35… より、約100人
- となります。
速さ
[編集]速さ
[編集]ここでは、特に速さについて学んでいきましょう。 例えば、ライオンが9秒間に、200mだけ走ったとします。また、キリンは、6秒間に100mだけ走ったとします。このとき、ライオンは1秒間におよそ22.2m,キリンは、1秒間におよそ16.7m走ったことになります。このように、ある時間あたり進める長さを速さといます。 速さはある時間あたりの速さを表すものですから、速さは
- 速さ=道のり÷時間
- という式で、求められます。
- 10÷60=0.16666…
より、およそ分速0.167kmに、つまり、およそ分速167mになります。
- 15×60=900
より、秒速15cmは、分速900cm、つまり分速9mとなります。
なお、「時速5km」を、「毎時5km」「5km/h[1]」などと表すこともあります。
- 問題1
あるマラソン選手が42.195kmを、2.2時間で走り終えました。この選手の速さは、時速何kmですか。
- 答え
式は42.1952.2 となります。これを計算すると 19.17…となるので、およそ時速19.2kmとなります。
速さの公式
[編集]速さ=道のり÷時間 であるから
- 道のりは 道のり=速さ×時間 という式で求められます。
- 同じように考えてみると
- 時間は 時間=道のり÷速さ という式で求められます。
- 問題2
- (1)時速40kmで3時間走った車は、何km進みましたか。
- (2)A君は、9kmはなれたところにあるおばさんの家に、時速15kmの自転車で向かっています。何分でつきますか。
(分速を求める方法と、何時間でつくか求める方法でやってみましょう)
割合
[編集]はじめに
[編集]5年生は200人いて、そのうち音楽をよく聞く人は100人です。一方、6年生は50人いて、 そのうち音楽をよく聞く人は30人です。 5年生と、6年生では、どちらの方が音楽をよく聞くといえるでしょうか。
それは、5年生と6年生で、全体の人数が
そこで、
たとえば、全体の人数を100人にそろえてみましょう。
5年生はもともと全体の人数が200人ですから、これを2でわって100人にします。
- 同時に、音楽好きな人の人数も2でわります。
<5年生> 全体の人数 :200人 --> 100人(2でわった) 音楽好きな人:100人 --> 50人(2でわった)
一方、6年生はもともとの全体の人数が50人ですから、これを2倍して100人にします。 同時に、音楽をよく聞く人の人数も2倍します。
<6年生> 全体の人数 : 50人 --> 100人(2倍した) 音楽好きな人: 30人 --> 60人(2倍した)
つまり、全体の人数が100人だったとすると、音楽をよく聞く人は、5年生では50人、6年生では60人 いることになります。
この結果、6年生の方が音楽をよく聞くと言えます。
ここでは全体の人数を100人にあわせましたが、もちろん他の数にしても同じ結果になるはずです。
それでは、全体の人数が1人だとして、同じように計算してみましょう。
5年生はもともと全体の人数が200人ですから、これを200でわって1人にします。 同時に、音楽をよく聞く人の人数も200でわります。
<5年生> 全体の人数 :200人 --> 1人 (200でわった) 音楽好きな人:100人 --> 0.5人 (200でわった)
一方、6年生はもともとの全体の人数が50人ですから、これを50で割って1人にします。 同時に、音楽好きな人の人数も50で割ります。
<6年生> 全体の人数 : 50人 --> 1人 (50で割った) 音楽好きな人: 30人 --> 0.6人 (50で割った)
つまり、全体の人数が1人だったとすると、音楽好きな人は、5年生で0.5人、6年生では0.6人 いることになります。
この結果、6年生の方が音楽好きであると言え、先ほどと同じ結果になりました。
この2つめの例のように、ある量(もとにする量という)を1としたとき、別のある量(くらべる量という)がある量の何倍かを表す数を
割合 といいます。
割合
[編集]割合というのは、「ある量(比べる量)が、ある別の量(もとにする量)の何倍かということです。 ですから、 割合 = くらべる量 ÷ もとにする量
- という式で求めることができます。
また、この式から、
- くらべる量 = もとにする量 × 割合、
- もとにする量 = くらべる量 ÷ 割合
- となります。
割合の表し方
[編集]割合は例えば「このりんごジュースは
百分率
[編集]0.01倍を 1
歩合
[編集]0.1倍を 1
割合を表すグラフ
[編集]この節は書きかけです。この節を編集してくれる方を心からお待ちしています。
割合を表すグラフには、
比例
[編集]2つの量で、一方が2倍、3倍、…となったとき、もう一方が2倍、3倍、…となるとき、2つの数量は
図形と比例
[編集]- 直方体において、高さが変わっていくとき、高さと体積は比例します。
- 三角形や平行四辺形において、高さが変わっていくとき、高さと面積は比例します。
平均
[編集]3つのコップに 160mL、210mL、230mL のジュースが入るので、これをAさん、Bさん、Cさんの3人で飲もうと思います。しかし、これでは、1人分の量が
- 3つのコップのジュースを合わせて、それを同じ量ずつ3つのコップに分けることにしました。このとき、3つのコップのジュースの量の合計は160+210+230=600 (mL) になるので、1人分の量は 600÷3=200 (mL) となります。
このように、いくつかの数量を、1つあたりの量が等しくなるようにならしたものを
| 平均の求め方 |
|
平均=合計÷ |
また、合計=平均×個数、個数=合計÷平均 となります。
- 問題1
8人に算数のテストを行ったところ、点数は
となりました。このテストの8人の平均点は何点ですか。
- 答え
平均 = 合計 ÷ 個数 なので
- (点)
となります。 なお、平均は小数や分数となることもあります。
また、、10人いるクラブの各メンバーの体重が、つぎのようなとき、
- データ1
| 番号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 体重(kg) | 60.3 | 57.9 | 65.4 | 56.1 | 53.6 | 62.7 | 70.0 | 55.8 | 67.1 | 63.1 | ||||||||||
体重の平均は
より、61.2 kg が平均の体重となります。
平均の扱 いかた
[編集]下の表は、ウィキ小学校の5年1組の、ある1週間の、本の
| 冊数・曜日 | 月 | 火 | 水 | 木 | 金 |
|---|---|---|---|---|---|
| 貸出冊数 | 8 | 5 | 0 | 6 | 9 |
この表では、水曜日に、0冊とまったく借りられていませんが、「0」のデータでも平均に
- 貸出冊数の平均は、 より、5.6冊です。
下は、Aさんの、5回の
| 回数 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 記録 | 158cm | 167cm | 161cm | 327cm | 164cm |
4回目に、ほかの記録と大きくはなれた「327cm」という記録が出ていますが、はかりまちがえてしまったようです。
- このような、記録ミスなどによる、大きくはなれたデータがあるときは、それをふくめずに平均を計算することがあります。
- ここでは、平均は
- で、平均は162.5cmです。
平均の求め方のくふう
[編集]あるグループの5人の身長は、145cm,156cm,149cm,141cm,152cm となっています。この5人の身長の平均を求めてみましょう。
- ふつうに計算すると となりますが、これを計算するのは少し大変です。
- そこで、くふうした平均の計算方法を考えてみましょう。
- まず、5人の身長はすべて140cmより高いので、「5人の身長と140cmの差」の平均を求めて、それに140をたす という方法で平均を求めてみましょう。
- まず、「5人の身長と140cmの差」の平均は となります。
- これに140をたすと 8.6+140=148.6 となり、これでも平均を求められます。
- また、一番身長の低い人の身長は、141cmです。そこで、「5人の身長と141cmの差」の平均を求めて、それに141をたす という方法で平均を求めてみましょう。
- まず、「5人の身長と141cmの差」の平均は となります。
- これに141をたすと 7.6+141=148.6 となり、これでも平均を求められます。
- このように、くふうして平均を求めることができます。
算数ドリル
[編集]下の「5年生のための算数ドリル」の文字を
見ているページが、算数ドリルのぺージに、変わります。
- ^ kmはキロメートル、hは英語で一時間を表す"hour"の意味です。この記号の意味は道のり(km)÷時間(h)、つまり分数で表すとkm/hとなるのです。























































































