小学校算数/6学年

式と計算

分数×整数

${\frac {b}{a}}\times {c}={\frac {b\times c}{a}}$ となります。

分数÷整数

${\frac {b}{a}}\div {c}={\frac {b}{c\times a}}$ となります。

分数×分数

分数のかけ算は、それぞれ真分数または仮分数の場合^[1]は分数の分子と分母を個別にかけ算すればできます。

つまり

{\frac {b}{a}}\times {\frac {d}{c}}={\frac {b\times d}{a\times c}}

となります。

例えば、

${\frac {1}{5}}\times {\frac {2}{3}}={\frac {1\times 2}{5\times 3}}={\frac {2}{15}}$

となります。

ただし帯分数がふくまれている場合は仮分数に直してからでなければいけません。これは分数の割り算も同じです。

$2{\frac {2}{3}}\times 1{\frac {2}{5}}={\frac {8}{3}}\times {\frac {7}{5}}={\frac {8\times 7}{3\times 5}}={\frac {56}{15}}\dots (=3{\frac {11}{15}})$

分数÷分数

逆数

逆数は分数の分子と分母を入れ替えた物になります。つまり、 ${\frac {b}{a}}$ の逆数は ${\frac {a}{b}}$ です。

分数のわり算

分数のわり算では、わられる数にわる数の逆数をかけると答えが得られます。

{\frac {b}{a}}\div {\frac {d}{c}}={\frac {b}{a}}\times {\frac {c}{d}}

となります。

なんでわり算では逆数をかけるの？

それでは、 ${\frac {b}{a}}\div {\frac {d}{c}}$ を例にして解説していきます。ここでまだわかっていない答えをとりあえず $x$ と書いておきます。

{\frac {b}{a}}\div {\frac {d}{c}}=x

割り算は割られる数と割る数に同じ数をかけても答えは同じになります。例えば

{\frac {b}{a}}\times e\div ({\frac {d}{c}}\times e)={\frac {b}{a}}\div {\frac {d}{c}}

整数÷分数の式に直せば計算できるので ${\frac {b}{a}}\times {\frac {a}{b}}\div ({\frac {d}{c}}\times {\frac {c}{d}})$ にすれば $1\div {\frac {d}{c}}\times {\frac {c}{d}}$ になるので計算できます。

文字と式

同じ値段(ねだん)のえん筆を6本買います。

えん筆1本の値段を50円としたとき、式は $50\times 6=300$ となります。

えん筆1本の値段を $\Box$ 円、6本の代金を $\triangle$ 円として、 $\Box$ と $\triangle$ の関係を式に表すと、 $\Box \times 6=\triangle$ となります。

これからは、 $\Box$ や $\triangle$ などの記号の代わりに、 $x$ (エックス)や $y$ (ワイ)などの文字を使うことがあります。

えん筆1本の値段を $x$ (エックス)円、6本の代金を $y$ (ワイ)円として、 $x$ と $y$ の関係を式に表すと、 $x\times 6=y$ となります。

$x=60$ のときは、 $x\times 6=y$ の $x$ に60をあてはめて計算すると、 $60\times 6=360$ となります

計算のきまりを文字の式で表そう

分配法則

(a+b)\times c=a\times c+b\times c

(a-b)\times c=a\times c-b\times c

交換法則

a+b=b+a

a\times b=b\times a

結合法則

(a+b)+c=a+(b+c)

(a\times b)\times c=a\times (b\times c)

量と測定

身近にある図形の面積

小学校算数/5学年までにw:平行四辺形やw:三角形等の図形の面積の求め方を学びました。しかし、実際に見られる図形は必ずしも完全な三角形ではなくでこぼこな図形などもあります。このような時にでもだいたいの面積を調べることができます。

例えば方眼紙に適当に書いた図形の面積を求めてみましょう。今までのやり方だとその図形の面積を求めることはできません。しかしだいたいの大きさなら調べることはできます。

方眼紙に書いた図形はたくさんのマスで区切られています。マスが完全にその図形にふまれている場合、マスの上を図形の線が通っています。そのマスの数を調べることによっておおよその面積を調べることができます。

1辺の長さが1cmの方眼で、図形が完全にふくまれているマスが100個、図形の線が通っているマスが20個ありました。その面積はいくらになりますか？

この図形の面積は、マス100個の面積よりも大きいことはすぐにわかります。そして、20個のマスは図形の線が通っていて、図形に完全にふくまれてはいないのですから、マス120個の面積よりは小さいことがわかります。だから、この場合はその図形の面積は $100cm^{2}$ と $120cm^{2}$ の間であることがわかります。これではまだ少しおおざっぱですが、方眼紙のマスをより細かくする(例えば5mmや1mm四方のマスにとりかえることによってよりくわしく面積を知ることができます。

ここで、「図形の線が通っているマス」の、図形がふくまれている部分の面積はわかりませんでしたが、すべてふくまれている面積が

0.5cm^{2}

とすると、この図形の面積は

110cm^{2}

となります。

あるいは、三角形や長方形など、面積を求められる図形に形を変えておよその面積を求めることもできます。

図形

対称(たいしょう)な図形

線対称(せんたいしょう)

ある直線を軸(じく)として図形を折り重ねたとき、元の図形とぴったり重なる図形は 線対称(せんたいしょう)であるといいます。

また、その折り重ねたときの軸となった直線を 対称の軸 といいます。

対応する2つの点を結ぶ直線は、対称の軸と垂直(すいちょく)に交わります。また、その交点と対応する点のきょりは、それぞれ等しくなります。

点対称(てんたいしょう)

ある図形をある点を中心に180°回転させたとき、もとの図形と重なる図形は 点対称(てんたいしょう)である といいます。また、その回転の中心の点を 対称の中心 といいます。

対応する2つの点を結ぶ直線は、対称の中心を通ります。また、対称の中心と、対応する2つの点を結ぶと、そのきょりは、それぞれ等しくなります。

多角形と対称

三角形と対称: 二等辺三角形は、線対称(たいしょう)な図形で, 対称の軸(じく)は1本あります。また、点対称な図形ではありません。また、正三角形も線対称な図形で, 対称の軸は3本あります。点対称な図形ではありません。

四角形と対称: 平行四辺形は、線対称ではありませんが、点対称です。長方形は線対称な図形で、対称の軸は4本あります。ひし形は線対称な図形で、対称の軸は2本あります。正方形は線対称な図形で、対称の軸は4本あります。

正多角形と対称: 正多角形において、線対称かどうか、対称の軸の本数、点対称かどうかについて調べると以下のようになります。

図形/内容	線対称かどうか	対称の軸の本数	点対称かどうか
正三角形	〇	3	×
正四角形(正方形)	〇	4	〇
正五角形	〇	5	×
正六角形	〇	6	〇

正多角形は必ず線対称で、対称の軸の本数はその正多角形の辺の数に等しくなっています。また、辺の数が奇(き)数の正多角形は点対称ではなく、偶(ぐう)数の正多角形は点対称となります。

円と対称: 円は線対称な図形で、対称の軸は直径となります。直径は無数にあるので、対称の軸も無数にあります。また、円は点対称な図形で、その対称の中心は円の中心となります。

円の面積

円の面積の求め方を考えてみましょう。

図のように、円をおうぎの形に等分し、並(なら)べかえます。

このとき、並びかえた図形は長方形(平行四辺形)とみることができます。

その縦(たて)の長さは、半径で、横の長さは 円周の長さの半分 と等しくなります。

円周=直径×円周率 で、

円周÷2=直径×円周率÷2=(直径÷2)×円周÷2=半径×円周率となるので、円周の半分の長さは半径×円周率と等しくなります。

この長方形の面積(縦×横)＝円周÷2×半径＝半径×円周率×半径となりますから、

円の面積は、 半径×半径×円周率 という式で求められることになります。ここでは円周率を3.14とします。

いろいろな図形の面積

この図形は、正方形の中に、円の一部を書いたものです。色のついた部分の面積の求め方を考えましょう。

図形の拡大と縮小

ある図形を、形をかえないで大きくすることを、その図形を 拡大(かくだい)するといいます。たとえば右の図では、ある点を中心に上の青い図形を拡大して、下の黒い図形に重ねました。

拡大された図を 拡大図 といいます。右の絵では、上の青い「L」の形をを基準に考えた場合は、下の黒い図のほうが拡大図です。

ある図形を、形をかえないで小さくすることを、その図形を 縮小(しゅくしょう)する といいます。たとえば右の図では、下の黒い「L」の形を縮小して、上の青い図形にしています。

縮小された図を 縮図(しゅくず)といいます。「縮小図」ではないので注意してください。右の図では、下の黒い「L」の形を基準に考えた場合は、上の青い形のほうが縮図です。

地図の縮尺(しゅくしゃく)も、縮図のような考え方です。例えば縮尺が25000分の1となっているなら、実際の25000分の1の大きさで、全く同じ形に書いてあります。また、本などを縮小コピーしたり、拡大コピーしてみましょう(コピー機には「縮小コピー」「拡大コピー」の機能があることが多いです)。やはり、原稿(げんこう)と同じように印刷されますが、大きさは変わっているはずです。

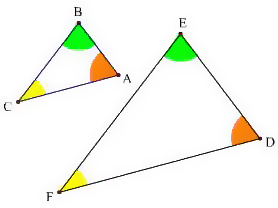
では、もっと簡単な図形である三角形はどうでしょうか。全く同じ形でも大きさが異(こと)なる三角形では、どのような共通の性質を持っているでしょうか。

この2つの三角形は、全く同じ形をしていますが、大きさが違います。この2つの三角形を比べると、次のことがいえます。

角A = 角D であり、角B = 角E であり、角C = 角F である。
AB:DE = BC:EF = CA:FD

(「AB」は、「辺ABの長さ」をさします)

三角形ABCを基準に考えてみれば、三角形DEFは、三角形ABCを拡大したものです。つまり、三角形DEFは、三角形ABCの拡大図です。

三角形DEFを基準に考えてみれば、三角形ABCは、三角形DEFを縮小したものです。つまり、三角形ABCは、三角形DEFの縮図です。

角柱と円柱の体積

角柱や円柱で、底面の面積を 底面積 といいます。

角柱は、多角形が底面に垂直(すいちょく)に動いたものと考えれば、その体積は「底面積×高さ」という式で求められます。

円柱も、角柱と同じようにその体積は「底面積×高さ」で求められます。

数量関係

ここでは、数量の間の関係について学んでいきましょう。

比

ウスターソースとケチャップを混ぜて、ハンバーグソースを作ろうと思います。

そこで、ウスターソースとケチャップを混ぜてハンバーグソースを作ってみました。

では、このウスターソースの量とケチャップの量の割合(わりあい)はどのように表せばよいでしょうか。

まず、ウスターソースの量はケチャップの何倍か考えてみましょう。

120\div 80=1.5

(倍)となりますね。(もしくは

{\frac {3}{2}}

倍)

このウスターソースとケチャップの割合を 120:80 と表すことがあります。

このような割合の表し方を 比(ひ) といい、比の記号「：」は「対(たい)」と読みます。

比の値

比 $a:b$ において、 $a$ が $b$ の何倍かを表す値(あたい)を 比の値(あたい) といいます。

a:b

の比の値は

{\frac {a}{b}}

となります。

等しい比

2つの比 3:4 と 9:12 について考えてみましょう。

比 3:4 の「3」と「4」に、3をかけると「9」「12」になるので 9:12に等しくなります。

また、3:4 と 9:12の比の値(あたい)を調べるとともに ${\frac {3}{4}}$ で、等しくなっています。

このように、2つの比の比の値が等しいとき、 2つの比は等しい といいます。

2つの比 $a:b$ と $c:d$ が等しいとき、 $a:b=c:d$ とかきます。なお、このような式を 比例式 といいます。

比 $a:b$ に、同じ数をかけたり割ったりしてもその比は等しくなります。

比を簡単にする

比を、同じ比の値で、できるだけ小さい整数の比に直すことを「比を簡単(かんたん)にする」 といいます。

問題

15:3を簡単にしましょう。

15と3の最大公約数は、3です。なので、3で15と3をわります。

15:3=5:1

5と1には最大公約数がないので、これ以上簡単になりません。

では、 ${\frac {1}{3}}:{\frac {3}{4}}$ を簡単にしてみましょう。

通分して、

{\frac {1}{3}}:{\frac {3}{4}}={\frac {4}{12}}:{\frac {9}{12}}=4:9

とすることができます。

また、

{\frac {1}{3}}:{\frac {3}{4}}

の比の値は

{\frac {1}{3}}\div {\frac {3}{4}}={\frac {4}{9}}

です。

これを使って 4:9 とすることもできます。

非が少数の場合

非が分数の場合

比を求める

問題　次のxにあてはまる数を求めましょう。

3:x=6:4

「3」と「6」に注目しましょう。6は3に2をかけた数なので、xはxに2をかけると4になる数だとわかります。だからxは4÷2=2 となります。

比を使った問題

(1)ウスターソースとケチャップを3:2の比で混ぜてハンバーグソースを作ります。ウスターソースを60mL使うとき、ケチャップは何mL必要ですか。

解答

[2]は、[1]の2倍、[3]は[1]の3倍を表す記号とします。

ウスターソースを[3]、ケチャップを[2]ずつ使うとすれば、

ウスターソースは60mL使うので、[3]は60mLだとわかります。

そのため、[2]にあたるケチャップは、60÷2×3=40(mL)必要です。これが答えです。

比の値を使って考えてみましょう。

ケチャップとウスターソースの比は 2:3 となります。ですから、比の値は

{\frac {2}{3}}

となります。ですから、ケチャップは

60\times {\frac {2}{3}}=40

(mL)とればよいことになります。

(2)AさんとBさんで、15枚(まい)のクッキーを、Aさんの枚数とBさんの枚数の比が $2:3$ になるように分けようと思います。AさんとBさんはそれぞれ何枚とればよいですか。

解答

[2]は、[1]の2倍、[3]は[1]の3倍を表す記号とします。

AさんとBさんがそれぞれ[2]、[3]ずつとるとすれば、

AさんとBさんは合わせて[5]をとることになります。

クッキーは15枚あるので、[1]はクッキー3枚分だとわかります。

そのため、Aさんは6枚、Bさんは9枚のクッキーをとることになります。これが答えです。

比の値を使って考えてみましょう。

Aさんの枚数と全体の枚数の比は 2:5 となります。ですから、比の値は

{\frac {2}{5}}

となります。ですから、Aさんは

15\times {\frac {2}{5}}=6

(枚)とればよいことになります。

また、Bさんの枚数と全体の枚数の比は 3:5 となります。ですから、比の値は

{\frac {3}{5}}

となります。ですから、Bさんは

15\times {\frac {3}{5}}=9

(枚)とればよいことになります。なお、15-6=9 と求めてもかまいません。

メモ

このような問題は、中学校で習う「方程式」を用いて計算されることがあります。

詳しくは中学校数学 1年生-数量を参照。

比例と反比例

さまざまなものの変わり方を調べてみましょう。

比例

一方の数量が2倍、3倍、…になると、もう一方の数量が2倍、3倍、…になるとき、2つの数量は比例(ひれい)するといいます。
(注意)参考書などでは、「正比例」と書かれている場合があります。

比例の関係を見るために、比例関係にある2数を用いて、表とグラフを作ってみよう。ここでは、「 $y=2\times x$ 」の比例の表、グラフを作る。

このとき、この比例の表は

比例の表
x	1	2	3	4	5
y	2	4	6	8	10

一方比例のグラフはファイル:Proportion.svg となる。

グラフを見ると分かる通り、比例のグラフは両方が0になる点を通る直線になる。

問題: $y=5\times x$ であるような比例の表とグラフを作りましょう。
解答

表は下のようになる。

比例の表
0	1	2	3	4	5	6	7	8	9	10
0	5	10	15	20	25	30	35	40	45	50

また、グラフはファイル:A Proportion.svg となる。

反比例

面積が12cm²の長方形において、縦(たて) の長さを変えたとき、横の長さはどうなるか調べてみましょう。

面積が12cm²の長方形の縦の長さと横の長さ
縦の長さ(cm)	0	1	2	3	4	5	6
横の長さ(cm)	(なし)	12	6	4	3	2.4	2

このように、一方の数量が 2倍、3倍、…になると、もう一方の数量が ${\frac {1}{2}}$ 倍、 ${\frac {1}{3}}$ 倍…になるとき、2つの数量は反比例しているといいます。

反比例のグラフ

反比例のグラフは、直線ではなく、右の図のようななめらかな曲線になります。

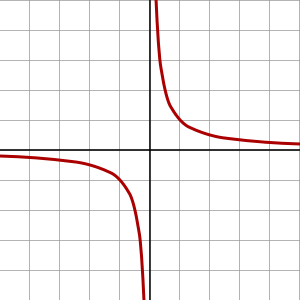
小学生は、右上部分以外は、気にしなくて構いません。中学校で、左上部分、左下部分、右下部分について習います。

場合の調べ方

この節は書きかけです。この節を編集してくれる方を心からお待ちしています。

A,B,C,D,Eの5つのチームが、ほかのチームと1回ずつ試合をします。

この時のすべての試合数を求めるとき、どうすればよいでしょうか。

このように、ほかのチームと何回か試合をするとき、(A対B)と(B対A）は同じものとして数えます。

データの調べ方

この節は書きかけです。この節を編集してくれる方を心からお待ちしています。

下は、ウィキ小学校の6年1組の30人のソフトボール投げの結果です。

ソフトボール投げの結果 (m)
28	15	22	34	27	9	42	31	11	37
10	27	20	38	21	43	34	7	25	36
17	24	35	14	27	19	32	9	40	29

階級(かいきゅう)


記録	人数
0m以上10ｍ未満	3人
10m以上20m未満	6人
20m以上30m未満	10人
30m以上40m未満	8人
40m以上50ｍ未満	3人
合計	30人

図のような、「10m以上20m未満」のような区間のことを階級と言います。また、このような階級が集まった表のことを度数分布表と言い、それぞれの階級の資料の個数を度数と言います。

平均値(へいきんち)

全ての値を足してそれを結果の数でわったものを平均値(へいきんち)と言います。

(28+15+22+\cdots +9+40+29)\div 30=24.2

中央値(ちゅうおうち)

全ての値を大きさの順で並べて奇数(きすう)の場合は真ん中、偶数(ぐうすう)の場合は真ん中の2つの数の平均をそれぞれ中央値(ちゅうおうち)といいます。

上の例の場合、大きい順に並べて13番目から18番目を見てみると

\cdots 24,25,27,27,27,28\cdots

記録の数は30で偶数なので、中央値は $(27+27)\div 2=27$ になります。

最頻値(さいひんち)

全ての値の中でもっともよく出てくる数を最頻値(さいひんち)といいます。

上の例では27が3回と一番多く出てるので、27が最頻値です。

(平均値、中央値、最頻値のことをまとめて代表値と呼びます。）

データを図にする

ドットプロット

資料を数直線上に並べ、同じ値のデータの個数だけドットを積み上げてあらわしたものを、ドットプロットと言います。

ドットプロットの例。上のソフトボール投げの例とは関係ない。

柱状グラフ

統計で度数分布を示すグラフです。横軸上に階級、縦軸上に度数を目盛り、おのおのの階級の上に、度数を高さとする長方形を立てたものです。ヒストグラムともよばれます。

算数ドリル

下の「6年生のための算数ドリル」の文字を押(お)すと、見ているページが、算数ドリルのぺージに、変わります。

6年生のための算数ドリル

^ 帯分数でない、左に数字がついていない分数のことです

[1] 帯分数でない、左に数字がついていない分数のことです

[1]