旧課程(2013年度-2021年度)高等学校数学I/数と式

数と集合

実数

無理数と有理数

${\sqrt {2}}$や$-{\sqrt {5}}$、$\pi$のように、分母分子が整数の分数で表すことはできない数を無理数という。それに対して、整数や循環小数など、分母分子が整数の分数で表すことのできる数を有理数という。

有理数と無理数を合わせて実数という。どんな実数でも数直線上の点として表せる。また、どんな実数も、有限小数あるいは無限小数として表せる。

${\sqrt {2}}$が無理数であることの証明（発展）

${\sqrt {2}}$ が有理数であると仮定すると、互いに素な（1以外に公約数をもたない）整数 m, n を用いて、

${\sqrt {2}}={\frac {m}{n}}$

と表わすことができる。このとき、両辺を2乗して分母を払うと、

$2n^{2}=m^{2}$ … (1)

よって m は2の倍数であり、整数 l を用いて $m=2l$ と表すことができる。これを (1) の式に代入して整理すると、

$2l^{2}=n^{2}$

よって n も2の倍数であるが、これは m, n が2を公約数にもつことになり、互いに素と仮定したことに矛盾する。したがって ${\sqrt {2}}$ は無理数である（背理法）。

無限小数

0.1 や 0.123456789 のように、ある位で終わる小数を 有限小数 という。

一方、$0.1234512345\cdots$ や $3.1415926535\cdots$ のように無限に桁が続く小数を 無限小数 という。

無限小数のうち、$0.\color {red}{3}\color {blue}{3}\color {green}{3}\cdots$や$0.1\color {red}{23}\color {blue}{23}\color {green}{23}\color {purple}{23}\cdots$、$0.\color {red}{142857}\color {blue}{142857}\cdots$のように、ある位より下から、ある数字の配列が繰り返されているものを 循環小数 という。

繰り返しの最小単位を 循環節 という。循環小数は循環節の始まりと終わりの部分に ・ をつけて表す。

• $0.333\cdots =0.{\dot {3}}$

• $0.1232323\cdots =0.1{\dot {2}}{\dot {3}}$

• $0.142857142817\cdots =0.{\dot {1}}4285{\dot {7}}$

である。

問題

次の分数を小数で表わせ。

(1) ${\frac {8}{5}}$

(2) ${\frac {7}{9}}$

(3) ${\frac {25}{11}}$

全ての循環小数は分母分子が整数の分数の形に表すことができる。

例

$0.{\dot {3}}$を分数で表す。

$a=0.333\cdots =0.{\dot {3}}$ (1)

と置くと、

$10a=3.333\cdots$ (2)

である。(2) - (1) より $9a=3$、よって $a={\frac {1}{3}}$ である。

$1.2{\dot {3}}{\dot {4}}$を分数で表す。

$a=1.23434\cdots =1.2{\dot {3}}{\dot {4}}$と置く。

このとき、

$10a=12.3434\cdots =12.{\dot {3}}{\dot {4}}$

$1000a=1234.{\dot {3}}{\dot {4}}$

なので、$1000a-10a=1234.{\dot {3}}{\dot {4}}-12.{\dot {3}}{\dot {4}}$より、$990a=1222$なので$a={\frac {611}{495}}$

例題

• (例題1)

${\begin{aligned}a&=0.{\dot {1}}4285{\dot {7}}\\1000000a&=142857.{\dot {1}}4285{\dot {7}}\\999999a&=142857\\a&={\frac {142857}{999999}}\ ={\frac {1}{7}}\end{aligned}}$

• (例題2)

${\begin{aligned}a&=0.1{\dot {2}}{\dot {3}}\\100a&=12.3{\dot {2}}{\dot {3}}\\99a&=12.2\\a&={\frac {12.2}{99}}\ ={\frac {61}{495}}\end{aligned}}$

絶対値

実数 a について、数直線上での a の原点からの距離を a の絶対値といい、$|a|$ で表す。

絶対値

$a\geqq 0$ のとき　　$|a|=a$ $a<0$ のとき　　$|a|=-a$

たとえば

$|2|=2$

$|-3|\ =\ -(-3)\ =\ 3$

である。

定義より $|a|=|-a|$ がいえる。また、$a,b$を任意の実数とするとき、それぞれに対応する数直線上の任意の2点 $\mathrm {P} (a),\mathrm {Q} (b)$ 間の距離については、次のことがいえる。

2点間の距離

数直線上の2点 $\mathrm {P} (a)$ と $\mathrm {Q} (b)$ の間の距離 $\mathrm {P} \mathrm {Q}$ は $|b-a|$ で表される。

• 例題

2点 $\mathrm {P} (5)$ と $\mathrm {Q} (-1)$ の間の距離を求めよ。

• 解答

$\mathrm {P} \mathrm {Q} =|5-(-1)|=6$ なので、よってPQ間の距離は 6 である。

平方根

2乗して a になる数を a の 平方根 という。 正の数の平方根は2つある。例えば、2乗して 1 になる数は 1 と -1 がある。

正の数aの平方根のうち、正であるものを${\sqrt {a}}$、負であるものを$-{\sqrt {a}}$と書く。また、0の平方根は0だけなので、${\sqrt {0}}=0$と定める。${\sqrt {a}}$はルートaと読む。

負の数の平方根は実数の範囲には存在しない。

平方根

正の数aの平方根は ${\sqrt {a}}$ と$-{\sqrt {a}}$ である。 0の平方根は0である。 負の数aの平方根は実数の範囲には存在しない。

${\sqrt {a}}$ と$-{\sqrt {a}}$ をまとめて $\pm {\sqrt {a}}$ と書くこともある。

• 問題

$2\ ,\ 4\ ,\ 9\ ,\ 12$の平方根を求めよ。

• 解答

$\pm {\sqrt {2}}\ ,\ \pm 2\ ,\ \pm 3\ ,\ \pm 2{\sqrt {3}}$

• 解説

それぞれのルートを計算し、$\pm$をつければよい。ただし、平方根のルールに従って、簡単化できるものは簡単化することが要求される。

例えば、$2$に対しては、$\pm {\sqrt {2}}$となる。

一般に、${\sqrt {A^{2}}}=|A|$である。

• 問題

次の値を求めよ。

(1) $({\sqrt {3}})^{2}$

(2) $(-{\sqrt {5}})^{2}$

(3) ${\sqrt {(-3)^{2}}}$

(4) ${\sqrt {({\sqrt {2}}-5)^{2}}}$

平方根を含む式の計算

根号について、次の公式が成り立つ。

平方根の公式

$a>0,b>0$ のとき ${\sqrt {a}}{\sqrt {b}}={\sqrt {ab}}$ 　　　（1） 　 ${\frac {\sqrt {a}}{\sqrt {b}}}={\sqrt {\frac {a}{b}}}$ 　　　（2）

公式(1)の証明

$({\sqrt {a}}{\sqrt {b}})^{2}=({\sqrt {a}})^{2}({\sqrt {b}})^{2}=ab$

であるから、${\sqrt {a}}{\sqrt {b}}$は$ab$の平方根である。また、${\sqrt {a}}>0,{\sqrt {b}}>0$であるから、${\sqrt {a}}{\sqrt {b}}$は正の数である。以上より、

${\sqrt {a}}{\sqrt {b}}={\sqrt {ab}}.$ //

公式(2)の証明

$\left({\frac {\sqrt {a}}{\sqrt {b}}}\right)^{2}={\frac {({\sqrt {a}})^{2}}{({\sqrt {b}})^{2}}}={\frac {a}{b}}$

であるから、${\frac {\sqrt {a}}{\sqrt {b}}}$は${\frac {a}{b}}$の平方根である。また、${\sqrt {a}}>0,{\sqrt {b}}>0$であるから、${\frac {\sqrt {a}}{\sqrt {b}}}$は正の数である。以上より、

${\frac {\sqrt {a}}{\sqrt {b}}}={\sqrt {\frac {a}{b}}}.$ //

さらに、上の公式(1)により、次の公式が導かれる。

公式

$a>0,k>0$ のとき ${\sqrt {k^{2}a}}=k{\sqrt {a}}$

• 問題

計算せよ。

1. 　${\sqrt {8}}{\sqrt {14}}$
2. 　$2{\sqrt {18}}+{\sqrt {50}}$
3. 　$\left({\sqrt {3}}-2{\sqrt {6}}\right)^{2}$

• 解答

1. 　${\sqrt {8}}{\sqrt {14}}\ =\ {\sqrt {8\times 14}}\ =\ {\sqrt {2^{4}\times 7}}\ =\ 2^{2}{\sqrt {7}}\ =\ 4{\sqrt {7}}$
2. 　$2{\sqrt {18}}+{\sqrt {50}}\ =\ 2\times 3{\sqrt {2}}+5{\sqrt {2}}\ =\ (6+5){\sqrt {2}}\ =\ 11{\sqrt {2}}$
3. 　まず、乗法公式 $(a-b)^{2}=a^{2}-2ab+b^{2}$を利用して展開する。詳細は「乗法公式」のセクションを参照のこと。

${\begin{aligned}\left({\sqrt {3}}-2{\sqrt {6}}\right)^{2}\ =\ \left({\sqrt {3}}\right)^{2}-2\times {\sqrt {3}}\times 2{\sqrt {6}}+\left(2{\sqrt {6}}\right)^{2}\ =\ 3-4{\sqrt {18}}+24\ =\ 27-4\times 3{\sqrt {2}}\ =\ 27-12{\sqrt {2}}\end{aligned}}$

分母に根号を含まない式にすることを、分母を有理化するという。有理化は、分母と分子に同じ数をかけてもよいことを利用して行う。

たとえば、${\frac {1}{\sqrt {2}}}$を有理化すると、${\frac {1}{\sqrt {2}}}\ =\ {\frac {1{\sqrt {2}}}{{\sqrt {2}}{\sqrt {2}}}}\ =\ {\frac {\sqrt {2}}{2}}$となる。

また、とくに${\frac {a}{b+c}}$について、$b^{2}-c^{2}=1$のとき、

${\frac {a}{b+c}}\ =\ {\frac {a(b-c)}{(b+c)(b-c)}}\ =\ {\frac {a(b-c)}{b^{2}-c^{2}}}\ =\ {\frac {a(b-c)}{1}}\ =\ a(b-c)$である。

たとえば、$a=1,b={\sqrt {2}},c=1$とすると、${\frac {1}{{\sqrt {2}}+1}}={\sqrt {2}}-1$である。

• 問題

分母を有理化せよ。

1. 　${\frac {\sqrt {2}}{\sqrt {12}}}$
2. 　${\frac {{\sqrt {2}}+2{\sqrt {3}}}{3{\sqrt {2}}-{\sqrt {3}}}}$

• 解答

1. 　${\frac {\sqrt {2}}{\sqrt {12}}}\ =\ {\frac {\sqrt {2}}{2{\sqrt {3}}}}\ =\ {\frac {{\sqrt {2}}{\sqrt {3}}}{2{\sqrt {3}}{\sqrt {3}}}}\ =\ {\frac {\sqrt {6}}{6}}$
2. 　${\frac {{\sqrt {2}}+2{\sqrt {3}}}{3{\sqrt {2}}-{\sqrt {3}}}}\ =\ {\frac {({\sqrt {2}}+2{\sqrt {3}})(3{\sqrt {2}}+{\sqrt {3}})}{(3{\sqrt {2}}-{\sqrt {3}})(3{\sqrt {2}}+{\sqrt {3}})}}\ =\ {\frac {6+{\sqrt {6}}+6{\sqrt {6}}+6}{(3{\sqrt {2}})^{2}-({\sqrt {3}})^{2}}}\ =\ {\frac {12+7{\sqrt {6}}}{18-3}}\ =\ {\frac {12+7{\sqrt {6}}}{15}}$

二重根号（発展）

二重根号とは、根号が2重になっている式のことである。二重根号は常に外せるわけではなく、根号の中に含まれる式によって簡単にできるかどうかが決まる。一般に、根号内の式が、$x^{2}$の形に変形できる場合には、外側の根号を外すことができる。

• 問題

${\sqrt {3+2{\sqrt {2}}}}$を簡単にせよ。

• 解答

$3+2{\sqrt {2}}$が$(\cdots )^{2}$の形にできるかを考える。

仮に、$({\sqrt {a}}+{\sqrt {b}})^{2}$(a,bは正の整数)の形にできるとすると、$3+2{\sqrt {2}}=a+b+2{\sqrt {ab}}$となり、

${\begin{cases}a+b&=3\\ab&=2\\\end{cases}}$

を満たす整数a,bを探せばよい。この関係は、a=1,b=2(a,bを入れ換えても可。)によって満たされるので、$3+2{\sqrt {2}}\ =\ ({\sqrt {2}}+1)^{2}$が成り立つ。

よって、${\sqrt {3+2{\sqrt {2}}}}\ =\ {\sqrt {({\sqrt {2}}+1)^{2}}}\ =\ {\sqrt {2}}+1$となる。

2重根号

$a>0\ ,\ b>0$ のとき ${\sqrt {(a+b)+2{\sqrt {ab}}}}={\sqrt {a}}+{\sqrt {b}}$ $a>b>0$ のとき ${\sqrt {(a+b)-2{\sqrt {ab}}}}={\sqrt {a}}-{\sqrt {b}}$

• 問題

次の式を計算せよ。

1. ${\sqrt {12-6{\sqrt {3}}}}$
2. ${\sqrt {3+{\sqrt {5}}}}$

• 解答

1. ${\sqrt {12-6{\sqrt {3}}}}\ =\ {\sqrt {12-2{\sqrt {27}}}}\ =\ {\sqrt {(9+3)-2{\sqrt {9\times 3}}}}\ =\ {\sqrt {9}}-{\sqrt {3}}\ =\ 3-{\sqrt {3}}$
2. ${\sqrt {3+{\sqrt {5}}}}\ =\ {\sqrt {\frac {6+2{\sqrt {5}}}{2}}}\ =\ {\frac {\sqrt {(5+1)+2{\sqrt {5\times 1}}}}{\sqrt {2}}}\ =\ {\frac {{\sqrt {5}}+{\sqrt {1}}}{\sqrt {2}}}\ =\ {\frac {{\sqrt {10}}+{\sqrt {2}}}{2}}$

集合

集合とは

中学では、たとえば「自然数のあつまり」とか「9以下の自然数のあつまり」とか「負の整数のあつまり」のようなものを、集合（しゅうごう）と読んできた。

では、数学でいう「集合」とは何か、これから考えていこう。

数学では、ある集まりのうち、さらに、それに属しているか属してないかを明確に区別できる条件のある物のあつまりを集合（set）という。例えば、「自然数」は「n > 0となる整数n の全体」という区別可能な条件があるので集合といえる。

しかし「大きな数」というあつまりは、どこからが「大きな」数といえるのかがはっきりしないため、数学の「集合」ではない。

ただし、「大きな数」を例えば「1億以上の整数」と区別できるように定義すれば集合になりえる。

さて、数学的な「集合」を構成するもの一つ一つのことを、その集合の 要素（element）という。

たとえば、「自然数の集合」の要素なら、自然数1や自然数2や自然数3、・・・などのひとつひとつの自然数がそれぞれ要素である。

「 1 は自然数の集合の要素である」といえる。

「 27 は自然数の集合の要素である」といえる。 例 7以下の自然数の集合の要素は、1と2と3と4と5と6と7 である。 （※ 範囲外？ ）なお、数学的には、区別がはっきりしさえすれば、例えば「△△高校の今の3年B組の生徒全員」等も集合として考えることができる。かならずしも「集合」とは「自然数」や「整数」などの数でなくてもいい。

集合と要素

aが集合Aの要素であるとする。このとき、aは集合Aに属する(ぞくする)といい、記号で、

a ∈ A

または 逆向きに

A $\ni$ a

と表す。

bがAの要素でないときは、

b $\notin$ A

または 逆向きに

A 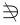b

と表す。

集合をあらわすとき、主に2種類の方法がある。（例は「10以下の自然数のうち偶数であるもの」の集合を表す。）

（1）　要素を書き並べる方法

（2）　要素の満たす条件を述べる方法

である

たとえば、「10以下の自然数のうち偶数であるもの」の集合を表す場合、（1）　の方法（要素を書き並べる方法）では、

{2, 　4, 　6, 　8, 　10}

となる。

一方、（2）の方法（要素の満たす条件を述べる方法）では、

{ x | x=2n (nは自然数), 2 ≤ x≤ 10 }

{ x | xは2以上10以下の偶数 }

{ 2n | 1 ≤ n≤ 5 (nは自然数) }

{ 2n | nは1以上5以下の自然数 }

などのようになる（何通りかある）。

備考

100以下の自然数の集合 A を、さきほどの（1）「要素を書き並べる方法」の方法で書く場合、

A ＝ {1, 　2, 　3, 　4, ・・・ , 99, 　100}

となる。また、この記法の「・・・」のように、要素の個数がとても多い場合や無数にある場合には、｛ ｝記号内の要素の途中を「・・・」または「……」、「…」などの点々で省略してよい。

（※ なお、ワープロで「……」などの短い点々を出したい場合、「三点リーダー」で変換すると出る。点が6つあっても「三点リーダー」で出る。

東京書籍の検定教科書で、短いほうの三点リーダーを使っている。啓林館などは、6つの点の長い三点リーダーを使っている。）

100以下の偶数の集合 B は、この記法（要素を書き並べる方法）では、

B ＝ {2,　 4, 　6, ・・・ , 98, 　100}

のようになる。

正の偶数全体の集合の要素は（1）「要素を書き並べる方法」の方法で書く場合、

{2, 　4, 　6, 　・・・}

のようにも書ける。

集合どうし

部分集合

集合Aが集合Bの部分集合である場合

2つの集合A,Bがあり、x∈A ならば x∈Bが成り立つとき、AはBの 部分集合 (ぶぶんしゅうごう、英：subset)であるといい、「BはAを含む」か「AはBに含まれる」という。この状態を記号で

A ⊂ B

または

B ⊃ A

で表す。

補足　　

Aの部分集合にはA自身もある。（つまり　A ⊂ A　である）。

また、A,B の集合の要素が同じとき、

A ＝ B

で表す。

例

集合 A ＝ {1, 2, 3} と 集合 B ＝ {1, 2 , 3 , 4, 5} があるとき、A は Bの部分集合である。

---

共通部分と和集合

色の部分は共通部分 A ∩ B

2つの集合A,Bがあるとき それらの両方の要素であるものの集合を AとBの 共通部分（きょうつうぶぶん）と呼び、

A ∩ B

と書く。

色の部分は和集合 A ∪ B

また、集合A,Bの少なくともどちらか一方には属している要素からなる集合のことを、AとBの和集合（union）と呼び、

A ∪ B

と書く。

3つの集合の共通部分と和集合

A ∩ B ∩ C

3つの集合 A, B, C については、3つのどれにも属する要素全体の集合を A,B,C の共通部分と呼び、

A ∩ B ∩ C で表す。

A ∪ B ∪ C

また、集合 A, B, C の少なくとも1つに属する要素の集合を A,B,C の和集合と呼び、

A ∪ B ∪ C で表す。

---

空集合

たとえば、「10以下の自然数のうちの偶数」の集合Aと、「10以下の自然数のうちの奇数」の集合Bについて、集合Aと集合Bの共通部分には、何も要素が無い。

この例のように、「要素がなにもない」という場合もあるので、数学では「要素がなにもない」場合もひとつの集合として考える。

要素をもたない集合のことを 空集合(くうしゅうごう、英：empty set あるいは null set)といい、記号は

$\varnothing$

であらわす。

ギリシャ文字のファイ（φ,$\phi \$）で表されることが多くあるが、厳密にはそれは誤りである。上の記号の他に$\emptyset$等も用いられるが、この教科書では、$\varnothing$を用いる。

補足

どのような集合Aにも、空集合は部分集合として含まれる。

つまり、空集合でないある集合をAとすると、

$\varnothing$ ⊂ A

である。

例

集合 { 1, 2 } の部分集合をすべて列挙すると、次の4つの集合になる。

φ ,　{1} ,　{2} ,　{1,2}

---

全体集合・補集合

色つきの部分が補集合 ${\overline {A}}$

集合 U を1つ設定し、その集合の要素や部分集合のみを考える場合を考える。このようなとき、集合Uを 全体集合（universal set） という。

全体集合Uの要素のうち、集合Aに属さないもの全体からなる集合のことをAの 補集合 （complement）といい、記号で補集合は ${\overline {A}}$と表す。

すなわち

${\overline {A}}$ ＝ {x | x∈U かつ x $\notin$ A}

である。

${\overline {({\overline {A}})}}$ は ${\overline {A}}$ の補集合を表す。　　${\overline {({\overline {A}})}}$ は ${\overline {\overline {A}}}$ と書く場合もある。

補集合について、次のことが成り立つ。 A∩A＝φ , 　　A∪A＝U , 　　${\overline {({\overline {A}})}}$ ＝A　

ド・モルガンの法則

${\overline {A\cap B}}={\overline {A}}\cup {\overline {B}}$

　

${\overline {A\cup B}}={\overline {A}}\cap {\overline {B}}$

下の図を用いて上の法則が正しい事を確かめよう。

• 
  2つの集合の一部に重なっている部分がある場合
• 
  片方がもう片方の部分集合である場合（AとB）と、集合同士が独立している場合（AとC）

• 
  3つある場合（AとB、BとC、CとA）
• 
  4つある場合（AとB、AとC、AとD、BとC、BとD、CとD）

• 問題

A={x|xは1以上20以下の2の倍数}・B={y|yは1以上20以下の3の倍数}とする時、以下に適する集合の要素を列挙せよ。ただし、全体集合U={z|zは1以上20以下の整数}とする。

1. ${\overline {A}}$
2. ${\overline {B}}$
3. $A\cap B$
4. $A\cup B$
5. $A\cup {\overline {B}}$
6. ${\overline {A\cap B}}$
7. ${\overline {A}}\cup {\overline {B}}$
8. $A\cap {\overline {A}}$
9. $B\cup {\overline {B}}$
10. $A\cap \varnothing$
11. $B\cup \varnothing$

• 解答

1. ${\overline {A}}$={1,3,5,7,9,11,13,15,17,19}
2. ${\overline {B}}$={1,2,4,5,7,8,10,11,13,14,16,17,19,20}
3. $A\cap B$={6,12,18}
4. $A\cup B$={2,3,4,6,8,9,10,12,14,15,16,18,20}
5. $A\cup {\overline {B}}$={1,2,4,5,6,7,8,10,11,12,13,14,16,17,18,19,20}
6. ${\overline {A\cap B}}$={1,2,3,4,5,7,8,9,10,11,13,14,15,16,17,19,20}
7. ${\overline {A}}\cup {\overline {B}}$={1,2,3,4,5,7,8,9,10,11,13,14,15,16,17,19,20}
8. $A\cap {\overline {A}}=\varnothing$
9. $B\cup {\overline {B}}=U$={1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20}
10. $A\cap \varnothing =\varnothing$
11. $B\cup \varnothing$= {3,6,9,12,15,18}

命題と証明

命題と条件

命題

数学的に正しいかどうかを明確に判断できる主張を命題（proposition）と呼ぶ。

ある命題が正しいとき、その命題は真（truth）であると呼ぶ。 命題が真でないとき、命題は偽（false）であると言う。

例

• 命題「7は素数である」は真である。
• 命題「11は偶数である」は偽である。
• 「5000は大きい数である」は命題ではない。なぜなら「大きい」という言葉の判断が主観的なものであり、判断に明確な基準が設定できないからである。

「実数$x$について、$x^{2}-4=0$である。」のように、$x$の値によって真偽の定まる主張を、$x$に関する条件という。

ならば

条件$p,q$について、$p$が真のとき、必ず$q$が真となるとき$p$ならば$q$といい、$p\Rightarrow q$とかく。このとき、条件$p$を仮定（assumption）、条件$q$を結論と呼ぶ。 これを表にすると以下のようになる。

p	q	$p\Rightarrow q$
真	真	真
真	偽	偽
偽	真	真
偽	偽	真

また、$p$が偽であるとき、$p\Rightarrow q$は無条件で真となる。なぜ？と思うかもしれないが、とっても自然なことである。たとえば、「エヌ氏が新宿にいる　ならば　エヌ氏は東京にいる」という命題について考える。エヌ氏が新宿にいるとき、「エヌ氏は新宿にいる」は真であり、「エヌ氏は東京にいる」も真であるので、「エヌ氏が新宿にいる　ならば　エヌ氏は東京にいる」は真である。次に、エヌ氏が渋谷にいるとき、「エヌ氏は新宿にいる」は偽であるが、「エヌ氏は東京にいる」は真である。最後に、エヌ氏が京都市にいるとき、「エヌ氏は新宿にいる」は偽であり、「エヌ氏は東京にいる」も偽である。 しかし、エヌ氏が渋谷や京都市にいるとき、仮定は偽であるが、「エヌ氏が新宿にいる　ならば　エヌ氏は東京にいる」という命題は正しい。

例

命題「$x^{2}=4$ならば$x=2$である」は$x=-2$もあてはまるので偽である。 命題${\rm {p\Rightarrow q}}$が偽であるときは、$p$は満たすが$q$を満たさない例が存在するときである。そのような例を反例（はんれい）という。命題が偽であることを示すには、反例を1つあげればよい。

• 問題

次の命題の真偽を判定し、偽の場合は反例も挙げよ。

1. 　$ab>0$ならば$a>0$かつ$b>0$である。
2. 　$a\geq b$かつ$b\geq a$ならば$a=b$である。
3. 　正三角形を2つ用意すればそれらは相似である。
4. 　素数ならば奇数である。

• 解答

1. 　偽(反例：$a=-1,b=-2$など)
2. 　真
3. 　真
4. 　偽(反例：2)

命題と集合

条件や条件を含む命題を考えることは、集合を考えることと同じである。

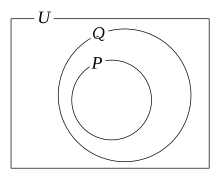
たとえば、実数 x について「x＞3 ならば x＞1 である」という命題は真である。

ここで「x＞3 である」という条件を p とし、また、x＞3 である数の集合を P としよう。つまり P＝｛x| x>3 ｝である。

同様に、「x＞1である」という条件を q とし、x＞1である数の集合を Q としよう。つまり Q＝｛x| x>1 ｝である。

このとき、命題 ${\rm {p\Longrightarrow q}}$ は真であるが、これは集合の包含関係 P⊂Q が成り立つことに対応している。

必要条件と十分条件

2つの条件 $p,q$ について、$p\Rightarrow q$が真であるとき、

$q$は$p$であるための 必要条件であるという。$p$が成り立つためには、まず、$q$が成り立つことが必要という意味だ。

$p$は$q$であるための 十分条件であるという。$q$が成り立つには、$p$が成り立てば十分という意味だ。

2つの条件 p,q について、

$p\Rightarrow q$と$q\Rightarrow p$の両方とも真であるとき、これを

${\rm {p\Longleftrightarrow q}}$

と書き、

pはqであるための必要十分条件である。または、pとqは同値であるという。

このとき、pとqを入れ替えることで、

qはpであるための必要十分条件である

ともいえる。

例

エヌ氏が新宿にいる　ならば　エヌ氏は東京にいる　という命題を考える。

エヌ氏が新宿にいるためには、まず、エヌ氏が東京にいる必要があるので、エヌ氏が東京にいることは、エヌ氏が新宿にいるための必要条件であるといえる。

エヌ氏が東京にいることを示すには、エヌ氏が新宿にいることを示せば十分なので、エヌ氏が新宿にいることは、エヌ氏が東京にいるための十分条件であるといえる。

「かつ」「または」と否定

「pかつq」に対応するP∩Q

「pまたはq」に対応するP∪Q

条件 p,q を満たすものの集合をそれぞれ P,Q とする。

このとき、条件「pかつq」および「pまたはq」をあらわす図は、それぞれ右図のようになる。

※ 数学における「または」の使い方では、「pまたはq」は、条件pと条件qの少なくともどちらか一方でも成り立っていればいい。

条件pに対し「pでない」の形の条件を pの 否定 （negation）といい、記号は ${\overline {p}}$で表す。

（※ 高校では習わないが、否定の意味として、 $\lnot {p}$という記号「¬」もある。）

条件を考えることは集合を考えることと同じなので、集合におけるド・モルガンの法則と同様に、条件においても、ド・モルガンの法則がなり立つ。 ド・モルガンの法則 p かつ q $\Longleftrightarrow$ p または q p または q $\Longleftrightarrow$ p かつ q

逆・裏・対偶

命題「 ${\rm {p\Longrightarrow q}}$ 」に対して

命題「${\rm {q\Longrightarrow p}}$」を 命題「 ${\rm {p\Longrightarrow q}}$ 」の 逆 （converse）

命題「${\rm {{\overline {p}}\Longrightarrow {\overline {q}}}}$」を 命題「 ${\rm {p\Longrightarrow q}}$ 」の 裏 （inverse）

命題「${\rm {{\overline {q}}\Longrightarrow {\overline {p}}}}$」を 命題「 ${\rm {p\Longrightarrow q}}$ 」の 対偶 （contraposition）

と呼ぶ。

これらは、たがいに右図のような関係にある。

---

たとえば、 もとの命題を

「$x=3\Longrightarrow x^{2}=9$」

だとすると、

裏は「$x\neq 3\Longrightarrow x^{2}\neq 9$」 であり

逆は「$x^{2}=9\Longrightarrow x=3$」 であり

対偶は「$x^{2}\neq 9\Longrightarrow x\neq 3$」である。

この命題の場合、もとの命題と対偶は、ともに真である。

いっぽう逆については x ＝ -3 という反例があるので、この命題の場合、逆は正しくない。また、裏も同様に、正しくない。

このような例から、次のことが分かる。 ある命題が真であっても、その命題の逆は、かならずしも真とは限らない。 また、ある命題が真であっても、その命題の裏は、かならずしも真とは限らない。

元の命題をその対偶を表にすると以下のようになる。

p	q	$p\Rightarrow q$	${\overline {q}}$	${\overline {p}}$	${\overline {q}}\Rightarrow {\overline {p}}$
真	真	真	偽	偽	真
真	偽	偽	真	偽	偽
偽	真	真	偽	真	真
偽	偽	真	真	真	真

この表からわかるように、元の命題とその対偶の真偽は一致する。

例

「エヌ氏が新宿にいる　ならば　エヌ氏は東京にいる」という命題の対偶は、「エヌ氏が東京にいない　ならば　エヌ氏は新宿にいない」である。

背理法

ある命題の結論を否定して、その否定のもとで矛盾が起こることを述べることで、 その命題が真であることを導出する仕方を背理法（proof by contradiction など）と呼ぶ。

たとえば、「Aではないことを証明せよ」という問題を解く時は「Aであると仮定する」と書き出して、仮定したことと矛盾する部分を作って「矛盾するのでAではない。」と証明を終える。

• 例題

素数は無限に存在する。

• 証明

素数が有限個であったと仮定する。すべての素数の積を$a$とすると、$a+1$はどの素数で割っても1余ることになり、1以外の自然数であって、素数の積に分解できないものが存在することになる。$a+1$の約数のうち1以外で最も小さいものを$b$とすると、$b$は1と$b$以外の約数を持たない。したがって$b$が素数であることになるが、$a+1$がどの素数でも割り切れないことと矛盾する。したがって、素数は有限個ではない。■

背理法と日常的な思考

背理法は多くの高校生が苦手としています。「Aである」ことを証明するために、わざわざ「Aでない」と仮定して矛盾を導くという論理の展開が不自然に感じられ、それが苦手意識につながっているようです。しかし、背理法の発想は私たちの日常的な思考でもよく使われています。ここでは、その例をいくつか紹介しましょう。

一つ目はアリバイ証明です。もしあなたが事件の犯人であると疑われたとします。そのとき、「自分が犯人ではない」ということをどのように証明しますか。ただ「自分は犯人ではない」と言うだけでは説得力がありません。この場合、犯行現場がA駅であったが、「自分は事件が起きたときにはB駅にいた」ことを証明できる、つまりアリバイが成り立つならば自分が犯人ではないという有力な証拠となります。この仕組みを簡単な文にすると以下のようになります。

私が犯人だと仮定すると、A駅にいたことになる。

しかし私はB駅にいた（＝A駅にいなかった）。

私が同じ時間にA駅とB駅の両方にいることはできないので、当初の仮定と矛盾する。

ゆえに私が犯人だという仮定がまちがっていたので、私は犯人ではない。

アリバイを示すことで自分の無実を証明するというのは、実はこういう仕組みになっているのです。なお、アリバイを示して無実を証明する方法には、やはり高校生の多くが苦手とする対偶証明法を使う方法もあります。そちらはみなさんで考えてみてください。

二つ目は消去法での選択肢の選び方です。たとえば、平成30年度「倫理」のセンター試験の大問1問7（マークシート番号7）の問題を見てみましょう。（バグと思わしき現象が起きたためリンクは貼りません。お手数ですが、各自確認して下さい。）　この正解を導き出すのに背理法の文章を利用してみましょう。

1が正解だと仮定すると、1の選択肢はグラフを正しく説明している。

しかし、2015年のトップ3（日伊独）と2050年のトップ3（日伊韓）は異なるので、正しい説明になっておらず、仮定と矛盾する。

ゆえに1を正解とした仮定は誤っていた。

だから、1の選択肢は正しくないので消す。

これを繰り返すと、誤った選択肢を消去して正解を導くことができますね（「倫理」の知識は全くいらないので、皆さんも挑戦してみてください）。

もちろん、アリバイ証明にしても消去法にしても、いつもこうした操作で解いているわけではありません。むしろ、背理法のことは意識しないで解くのが当たり前でしょう。実は背理法の考え方は本来、何気なく実行できるくらい自然な発想なのです。ほかにも、皆さんの日常的な考え方の中に背理法の形にそうものがあるはずです。逆に一見正しい背理法に見えても、実はインチキな論理展開のものもあるでしょう。そうしたことを探していくのも論理的に考えるためのトレーニングになります。ぜひ、挑戦してみてください。

式

式の展開と因数分解

整式

3や12などの定数や、$x$ や $y$ などの変数の積で表すことのできる式を単項式（たんこうしき、monomial）という。

次のようなものが単項式である。

• $3x$
• $12y$
• $0$
• $-x$
• $256xy^{2}$

単項式ではないもの例は以下である。

• ${\sqrt {x}}$
• ${\frac {1}{x}}$

1つ以上の単項式の和で表すことのできる式を多項式(polynomial)または整式という。

以下は多項式の例である。

• $3x+12y$
• $5+a-13x^{2}y$
• $a^{2}+2ab+b^{2}$
• $x-y$
• $2$
• 問題

次の式のうち単項式であるものを答えよ。

(1) 　$ax^{2}\times bx\times c$

(2)　$-(x^{3}y^{4})(z^{5})$

(3) 　$a^{2}+b^{2}+c^{2}-ab-bc-ca$

• 解答

(1), (2) が単項式。 (3) は項が6つあるため単項式ではない。

多項式の整理

$3x^{2}+5x^{2}+8x$ における $3x^{2}$ と $5x^{2}$ のように、多項式の文字と指数が同じである項を同類項（どうるいこう、like terms）という。

同類項は分配法則 $ab+ac=a(b+c)$ を使ってまとめることができる。たとえば $3x^{2}+5x^{2}+8x=(3+5)x^{2}+8x=8x^{2}+8x$である。$8x^{2}$ と $8x$ は文字は同じであるが指数が異なるので、同類項ではない。

• 問題

次の多項式の同類項を整理せよ。

1. 　$4x^{3}-3xy-2+1-3x^{3}+4xy$
2. 　$2a^{2}-4ab+2a-4ab^{2}-4a^{2}b$
3. 　$9x^{2}y^{3}z^{4}-8z^{2}y^{3}x^{4}+7zyx-6xyz+5x^{2}yz-4y^{2}xz+3zx^{2}y-2x^{4}y^{3}z^{2}$

• 解答

1. 　$x^{3}+xy-1$
2. 　$2a^{2}-4ab+2a-4ab^{2}-4a^{2}b$
3. 　$-10x^{4}y^{3}z^{2}+9x^{2}y^{3}z^{4}+8x^{2}yz-4xy^{2}z+xyz$

次数

$3x$ という単項式は、3という数と $x$ という文字に分けて考えることができる。数の部分を単項式の係数（けいすう、coefficient）という。

たとえば $-x=(-1)x$ という単項式の係数は -1 である。

$256xy^{2}$ という単項式は、256という数と $x,y,y$ という文字に分けて考えることができるので、この単項式の係数は256である。一方、掛けあわせた文字の数を単項式の次数（じすう、degree）という。$256xy^{2}$ は $x,y,y$ という3つの文字を掛けあわせてできているので、この単項式の次数は3である。0という単項式の次数は $0=0x=0x^{2}=0x^{3}=\cdots$と一つに定まらないので、ここでは考えない。

単項式の係数と次数は、単に数と文字に分けて考えるのではなく、ある文字を変数として見たときに、残りの文字を定数として数と同じように扱うことがある。

たとえば $-5abcx^{3}$という単項式を、$x^{3}$ だけが変数で、残りの文字 $a,b,c$ は定数と考えることもできる。 このとき$(-5abc)x^{3}$ と分けられるので、この単項式の係数は $-5abc$、変数は $x^{3}$ で、次数は3であるといえる。

このことを $-5abcx^{3}$ という単項式は、「$x$ に着目すると、係数は $-5abc$、次数は3である」などという場合がある。

あるいは $-5abcx^{3}$ の $a$ と $b$に着目すれば、$(-5cx^{3})ab$ と分けられ、$a$ と $b$ に着目したときのこの単項式の係数は $-5cx^{3}$、変数は $ab$ で、次数は2であるといえる。

慣習的には $a,b,c,\cdots$ などのアルファベットの最初の方の文字を定数を表すのに使い、$\cdots ,x,y,z$ などのアルファベットの最後の方の文字を変数を表すのに用いるが、一般的にはこの限りでない。

多項式の次数とは、多項式の同類項をまとめたときに、もっとも次数の高い項の次数をいう。たとえば $x^{3}+3x^{2}y+2y$ では、もっとも次数の高い項は $x^{3}$ であるので、この多項式の次数は3である。もし $x^{3}+3x^{2}y+2y$（$x$ は定数）であれば、すなわち多項式の $y$ について着目すると、もっとも次数の高い項は $3x^{2}y$ と $2y$ であるので、この多項式の次数は1である。このとき着目した文字を含まない項 $x^{3}$ は定数項（ていすうこう、constant term）として数と同じように扱われる。

• 問題

次の多項式の $x$ または $y$ に着目したときの次数と定数項をそれぞれいえ。

1. $x^{6}+10xy^{2}+8x^{4}y+y^{5}-1$
2. $-ad-bcx^{2}-bc+2x^{3}y^{2}+y^{100}$
3. $pxy+q^{9}y^{2}+pqxy-p^{8}q^{3}x^{2}y+px^{4}y^{3}+pq^{2}x^{3}y^{4}$

• 解答

1. $x$ に着目すると6次式、定数項は $y^{5}-1$。$y$ に着目すると5次式、定数項は $x^{6}-1$。
2. $x$ に着目すると3次式、定数項は $-ad-bc+y^{100}$。$y$ に着目すると100次式、定数項は $-ad-bcx^{2}-bc$。
3. $x$ に着目すると4次式、定数項は $q^{9}y^{2}$。$y$ に着目すると4次式。定数項は存在しない。

降べきと昇べき

たとえば、

$x^{2}+6x+7$

のように、次数の高い項から先に項をならべることを降べき（こうべき）という。

※ なお、次数の大小については、次数が大きいことを「次数が高い」と言ったりしてもよい。つまり、次数の大小については、高低で言い換えてもよい。

さて、式を使う目的によっては、次数のひくい項から先に書いたほうが便利な場合もある。

たとえば、$x$が 約0.01 のような1未満の小さい数の場合、式 $x^{2}+6x+7$ の値を求めたいなら、文字$x$の次数の小さい項のほうが影響が高い。

なので、 目的によっては

$7+6x+x^{2}$

のように、次数のひくい項から先に書く場合もある。

$7+6x+x^{2}$ のように、次数の低い項から先に項をならべることを昇べき（しょうべき）という。

演習問題

次の式をそれぞれ、降べき、昇べきの順に並べよ。

1. $x-1+x^{2}$
2. $-1+x^{3}+3x-x^{2}$

解答

1. 降べき$x^{2}+x-1$、昇べき$-1+x+x^{2}$
2. 降べき$x^{3}-x^{2}+3x-1$、昇べき$-1+3x-x^{2}+x^{3}$

特定の文字への着目

多項式に2つ以上の文字があるとき、特定の1つの文字に注目して並び変えると、使いやすくなることがある。

たとえば、

$x^{3}-5+2xy^{3}+7y^{2}+6x^{2}y$　　（例1）

の項を、xの次数が多い項から先に並びかえ、同類項をまとめると

$x^{3}+(6y)x^{2}+(2y^{3})x+(7y^{2}-5)$　　（例2）

となる。

この（例2）のように、特定の文字だけに着目して、その文字の次数の高い順に並びかえると便利なこともしばしばある。

(例2)は、$x$について降べきの順に並び変えた多項式である。

着目してない文字については、並び換えのときは定数のように扱う。

いっぽう、$x$について、次数のひくい項から順に並べると、次のような式になる。

$(7y^{2}-5)+(2y^{3})x+(6y)x^{2}+x^{3}$　　（例3）

このように、特定の文字の次数が低いものから順に並びかえると便利なこともしばしばある。

例3は、xについて 昇べき の順に並び変えた多項式である。

特定の文字に注目した次数

たとえば、式

$y=ax+b$

という式の右辺

$ax+b$

の次数は、いくらであろうか。

aとxを等しく文字として扱うのであれば、$ax$の次数は

$a^{1}x^{1}$

より 1＋1 ＝2 なので、この式の次数は2である。（項bは次数1なので、$ax$の次数2よりも低いので無視する。）

しかし、もしこの式を、定数$a$を係数とする変数$x$についての一次関数とみるのであれば、一次式と思うのが合理的だろう。

このような場合、特定の文字だけに注目したその式の次数を考えるとよい。

たとえば、文字xだけに注目して、式 $ax+b$ の次数を決めてみよう。

すると、文字xに注目した場合の式 $ax+b$ の次数は1になる。

なぜなら

文字$x$に注目した場合の式 $a$ の次数は0である。

文字$x$に注目した場合の式 $b$ の次数は0である。

文字$x$に注目した場合の式 $x$ の次数は1である。

よって、文字$x$に注目した場合の項 $ax$ の次数は、 0＋1 なので、1である。

このように考える場合、必要に応じてどの文字に注目したかを明記して「文字◯◯に注目した次数」のように述べるとよい。

多項式の計算

多項式の積は分配法則を使って計算することができる。

例

$(2x+1)(3x+4)=3x(2x+1)+4(2x+1)=6x^{2}+11x+4$

このように多項式の積で表された式を複数の単項式の和の形にすることを、多項式を展開（てんかい、expand）するという。

ここで、$(ax+b)(cx+d)$を展開しよう。

$A=ax+b$とおくと、$A(cx+d)=Acx+Ad=(ax+b)cx+(ax+b)d=acx^{2}+bcx+adx+bd=acx^{2}+(ad+bc)x+bd$

つまり、$({\color {red}a}x+{\color {blue}b})({\color {magenta}c}x+{\color {green}d})={\color {red}a}{\color {magenta}c}x^{2}+({\color {red}a}{\color {green}d}+{\color {blue}b}{\color {magenta}c})x+{\color {blue}b}{\color {green}d}$である。

指数法則

$a$ を $n$ 回掛けたものを $a^{n}$ と書き、aのn乗（-じょう、a to the n-th power）という。ただし $a^{1}=a$ と定義する。たとえば、

$2^{1}=2$

$2^{2}=2\times 2=4$

$2^{3}=2\times 2\times 2=8$

である。$a,a^{2},a^{3},a^{4},a^{5},\cdots$ を総称して $a$ の累乗（るいじょう、exponentiation）という。$a^{n}$ の $n$ を指数（しすう、exponent）という（$a$ は底（てい、base）という）。

累乗どうしを掛けあわせた積は、次のように計算することができる。

${\begin{aligned}a^{2}\times a^{3}&=(a\times a)\times (a\times a\times a)\\&=a^{2+3}\\&=a^{5}\end{aligned}}$

累乗どうしを割った商は、次のように計算することができる。

${\begin{aligned}a^{3}\div a^{2}&={\frac {a\times a\times a}{a\times a}}\\&={\frac {a}{1}}\\&=a\end{aligned}}$

累乗の累乗は、次のように計算することができる。

${\begin{aligned}(a^{2})^{3}&=a^{2}\times a^{2}\times a^{2}\\&=a^{2+2+2}\\&=a^{2\times 3}\\&=a^{6}\end{aligned}}$

積の累乗は、次のように計算することができる。

${\begin{aligned}(ab)^{2}&=a\times b\times a\times b\\&=a\times a\times b\times b\\&=a^{2}b^{2}\end{aligned}}$

これらをあわせて指数法則（しすうほうそく、exponential law）という。

指数法則

m, n を正の整数とすると、 $a^{m}\times a^{n}=a^{m+n}$ $a^{m}\div a^{n}=a^{m-n},m>n$ $(a^{m})^{n}=a^{mn}$ $(ab)^{n}=a^{n}b^{n}$

指数法則の証明

累乗の定義より明らか。

${\begin{aligned}a^{m}\times a^{n}&=\overbrace {\underbrace {(a\times a\times \cdots \times a)} _{m}\times \underbrace {(a\times a\times \cdots \times a)} _{n}} ^{m+n}\\&=a^{m+n}\end{aligned}}$

${\begin{aligned}a^{m}\div a^{n}&={\frac {\overbrace {a\times a\times \cdots \times a} ^{m}}{\underbrace {a\times a\times \cdots \times a} _{n}}}\\&={\frac {\overbrace {a\times a\times \cdots \times a} ^{n}\times \overbrace {a\times a\times \cdots \times a} ^{m-n}}{\underbrace {a\times a\times \cdots \times a} _{n}}}\\&={\frac {\overbrace {a\times a\times \cdots \times a} ^{m-n}}{1}}\\&=\underbrace {a\times a\times \cdots \times a} _{m-n}\\&=a^{m-n}\end{aligned}}$

${\begin{aligned}(a^{m})^{n}&=\underbrace {a^{m}\times a^{m}\times \cdots \times a^{m}} _{n}\\&=a^{\overbrace {m+m+\cdots +m} ^{n}}\\&=a^{mn}\end{aligned}}$

${\begin{aligned}(ab)^{n}&=\underbrace {(a\times b)\times (a\times b)\times \cdots \times (a\times b)} _{n}\\&=\underbrace {(a\times a\times \cdots \times a)} _{n}\times \underbrace {(b\times b\times \cdots \times b)} _{n}\\&=a^{n}b^{n}\end{aligned}}$

• 問題

次の式を計算しなさい。

1. $x^{4}\times x^{3}$
2. $(a^{3})^{4}$
3. $(-a^{2}b)^{3}$

• 解答

1. $x^{4}\times x^{3}=x^{4+3}=x^{7}$
2. $(a^{3})^{4}=a^{3\times 4}=a^{12}$
3. $(-a^{2}b)^{3}=(-1)^{3}(a^{2})^{3}b^{3}=-a^{2\times 3}b^{3}=-a^{6}b^{3}$

乗法公式

• 問題

次の式を展開せよ。

1. $(a+b)^{2}$
2. $(a-b)^{2}$
3. $(a+b+c)^{2}$
4. $(a-b-c)^{2}$

• 解答

1. ${\begin{aligned}(a+b)^{2}&=(a+b)(a+b)\\&=a(a+b)+b(a+b)\\&=(aa+ab)+(ba+bb)\\&=aa+ab+ba+bb\\&=a^{2}+2ab+b^{2}\end{aligned}}$
2. ${\begin{aligned}(a-b)^{2}&=\{a+(-b)\}^{2}\\&=a^{2}+2a(-b)+(-b)^{2}\\&=a^{2}-2ab+b^{2}\end{aligned}}$
3. ${\begin{aligned}(a+b+c)^{2}&=\{(a+b)+c\}^{2}\\&=(a+b)^{2}+2(a+b)c+c^{2}\\&=(a^{2}+2ab+b^{2})+(2ac+2bc)+c^{2}\\&=a^{2}+2ab+b^{2}+2ac+2bc+c^{2}\\&=a^{2}+b^{2}+c^{2}+2ab+2bc+2ca\end{aligned}}$
4. ${\begin{aligned}(a-b-c)^{2}&=a^{2}+(-b)^{2}+(-c)^{2}+2a(-b)+2(-b)(-c)+2(-c)a\\&=a^{2}+b^{2}+c^{2}-2ab+2bc-2ca\end{aligned}}$

まとめると、次のようになる。

展開の公式

$(a+b)^{2}=a^{2}+2ab+b^{2}$ $(a-b)^{2}=a^{2}-2ab+b^{2}$ $(a+b)(a-b)=a^{2}-b^{2}$ $(x+a)(x+b)=x^{2}+(a+b)x+ab$ $(ax+b)(cx+d)=acx^{2}+(ad+bc)x+bd$ $(a+b+c)^{2}=a^{2}+b^{2}+c^{2}+2ab+2bc+2ca$

• 問題

次の式を展開しなさい。

1. $(a+2b)^{2}$
2. $(3x-5y)^{2}$
3. $(4x-3y)(4x+3y)$
4. $(x+1)(x-5)$
5. $(3x+2y)(2x-y)$

• 解答

1. $a^{2}+2\times a\times 2b+(2b)^{2}=a^{2}+4ab+4b^{2}$
2. $(3x)^{2}-2\times 3x\times 5y+(5y)^{2}=9x^{2}-30xy+25y^{2}$
3. $(4x)^{2}-(3y)^{2}=16x^{2}-9y^{2}$
4. $x^{2}+\{1+(-5)\}x+1\times (-5)=x^{2}-4x-5$
5. $(3\times 2)x^{2}+\{3\times (-y)+2y\times 2\}x+2y\times (-y)=6x^{2}+xy-2y^{2}$

乗法公式の利用

複雑な式の展開は、式の一部分を一つの文字において公式を使うとよい。

• 問題

次の式を展開しなさい。

1. $(a+3b-2c)^{2}$
2. $(x+y+4)(x-3y+4)$
3. $\left(x^{2}-2x+3\right)\,\left(x^{2}+2x-3\right)$

• 解答

1. $a+3b=A$とおくと

${\begin{aligned}(a+3b-2c)^{2}&=(A-2c)^{2}\\&=A^{2}-4cA+4c^{2}\\&=(a+3b)^{2}-4c(a+3b)+4c^{2}\\&=a^{2}+6ab+9b^{2}-4ca-12bc+4c^{2}\\&=a^{2}+9b^{2}+4c^{2}+6ab-12bc-4ca\\\end{aligned}}$

1. $x+4=A$とおくと

${\begin{aligned}(x+y+4)(x-3y+4)&=(A+y)(A-3y)\\&=A^{2}-2yA-3y^{2}\\&=(x+4)^{2}-2y(x+4)-3y^{2}\\&=x^{2}+8x+16-2xy-8y-3y^{2}\\&=x^{2}-3y^{2}-2xy+8x-8y+16\\\end{aligned}}$

1. $2x-3=A$とおくと

${\begin{aligned}\left(x^{2}-2x+3\right)\,\left(x^{2}+2x-3\right)&=\left\{x^{2}-(2x-3)\right\}\left\{x^{2}+(2x-3)\right\}\\&=\left(x^{2}-A\right)\,\left(x^{2}+A\right)\\&=x^{4}-A^{2}\\&=x^{4}-(2x-3)^{2}\\&=x^{4}-(4x^{2}-12x+9)\\&=x^{4}-4x^{2}+12x-9\\\end{aligned}}$

因数分解

因数分解の公式 1

$a^{2}+2ab+b^{2}=(a+b)^{2}$ $a^{2}-2ab+b^{2}=(a-b)^{2}$ $a^{2}-b^{2}=(a+b)(a-b)$ $x^{2}+(a+b)x+ab=(x+a)(x+b)$ $acx^{2}+(ad+bc)x+bd=(ax+b)(cx+d)$

• 問題

次の式を因数分解しなさい。

1. 　$2abc-4ab^{2}$
2. 　$x^{2}+6x+9$
3. 　$4a^{2}-4ab+b^{2}$
4. 　$64x^{2}-9y^{2}$
5. 　$x^{2}-x-6$
6. 　$3x^{2}+2x-5$
7. 　$6x^{2}+xy-y^{2}$

• 解答

1. 　${\color {red}2ab}\times c-{\color {red}2ab}\times 2b={\color {red}2ab}(c-2b)$
2. 　$x^{2}+2\times x\times 3+3^{2}=(x+3)^{2}$
3. 　$(2a)^{2}-2\times 2a\times b+b^{2}=(2a-b)^{2}$
4. 　$(8x)^{2}-(3y)^{2}=(8x+3y)(8x-3y)$
5. 　$x^{2}+\{2+(-3)\}x+2\times (-3)=(x+2)(x-3)$
6. 　$(1\times 3)x^{2}+\{1\times 5+(-1)\times 3\}x+(-1)\times 5=(x-1)(3x+5)$
7. 　$(2\times 3)x^{2}+\{2\times (-y)+y\times 3\}x+y\times (-y)=(2x+y)(3x-y)$

いろいろな因数分解

• 問題

次の式を因数分解しなさい。

1. 　　$3xy^{3}+81x$
2. 　　$(x-5)^{2}-9y^{2}$
3. 　　$x^{2}+xy+y-1$
4. 　　$x^{2}+xy-2y^{2}+2x+7y-3$

• 解答

1. ${\begin{aligned}3xy^{3}+81x&=3x(y^{3}+27)\\&=3x(y^{3}+3^{3})\\&=3x\left(y+3\right)\,\left(y^{2}-y\times 3+3^{2}\right)\\&=3x\left(y+3\right)\,\left(y^{2}-3y+9\right)\\\end{aligned}}$
2. 　　$x-5=A$とおくと

${\begin{aligned}(x-5)^{2}-9y^{2}&=A^{2}-9y^{2}\\&=(A+3y)(A-3y)\\&=\left\{(x-5)+3y\right\}\left\{(x-5)-3y\right\}\\&=(x+3y-5)(x-3y-5)\\\end{aligned}}$

1. 　　最も次数の低い $y$ に着目して整理すると

${\begin{aligned}x^{2}+xy+y-1&=(x+1)y+\left(x^{2}-1\right)\\&=(x+1)y+(x+1)(x-1)\\&=(x+1)\left\{y+(x-1)\right\}\\&=(x+1)(x+y-1)\\\end{aligned}}$

1. 　　$x$ に着目して整理すると

${\begin{aligned}x^{2}+xy-2y^{2}+2x+7y-3&=x^{2}+(y+2)x-(2y^{2}-7y+3)\\&=x^{2}+(y+2)x-(y-3)(2y-1)\\&=\left\{x-(y-3)\right\}\left\{x+(2y-1)\right\}\\&=(x-y+3)(x+2y-1)\\\end{aligned}}$

対称式と交代式

;対称式

　$a^{2}+b^{2}$ は、$a$ と $b$ を入れ替えて $b^{2}+a^{2}$ にしても、値はもとの式と同じままである。

このように、文字を入れ替えても同じままになる式のことを 対称式（たいしょうしき）という。

$a$,$b$ の対称式のうち、式 $a+b$ と 式 $ab$ の2つを 基本対称式 という。

基本対称式いがいの対称式は、基本対称式の加減乗除で表すことができる。たとえば、

$a^{2}+b^{2}=(a+b)^{2}-2ab$

である。

交代式

　$a^{2}-b^{2}$ は、文字を入れ替えると、$b^{2}-a^{2}$ になるが、これはもとの式を ー1 倍したものである。このように、文字を入れ替えることで、もとの式を ー1 倍したものになる式のことを 交代式 （こうたいしき）という。

一次不等式

同じ大きさの量を=で結んだ式を方程式と呼ぶことを既に学習した。ここでは、異なった量の大きさの違いを表す記号を導入し、その性質についてまとめる。

ある数A,Bがあるとき、AがBより大きいことを$A>B$と表し、AがBより小さいことを$A<B$と表す。ここで、<と>のことを不等号と呼び、このような式を不等式と呼ぶ。また、$\leq ,\geq$も似た意味の不等式であるが、それぞれAとBが等しい値である場合を含むものである。

なお、日本の教育においては、$\leq ,\geq$の代わりに、不等号の下に等号を記した$\leqq ,\geqq$を使うことが多い。

• 例

$x>7$という不等式があるとき、xは7より大きい実数である。また、$x\geq 7$の時には、xは7以上の実数である。

不等式では等式と同じように、両辺に演算をしても不等号の関係が変わらないことがある。例えば、両辺に同じ数を足しても、両辺の大小関係は変化しない。ただし、両辺に負の数をかけたときには、不等号の向きが変化することに注意が必要である。これは、負の数をかけると両辺の値は、0を中心に数直線を折り返した地点に移されることによる。

x < y ならば x + a < y + a.

x < y かつ a > 0 ならば ax < ay.

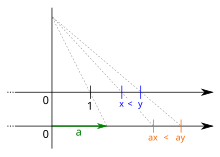x < y かつ a < 0 ならば ax > ay.

不等式の性質

1. 　　$a<b$ ならば、$a+c<b+c$，$a-c<b-c$

2. 　　$a<b$，$c>0$ ならば、$ac<bc$，${\frac {a}{c}}<{\frac {b}{c}}$

3. 　　$a<b$，$c<0$ ならば、$ac>bc$，${\frac {a}{c}}>{\frac {b}{c}}$

• 例

$x>y$が成り立つときには、$x+3>y+3$、$4x>4y$も成り立つ。また、$-x<-y$が成り立つ。

不等式の性質を使って

$a{\color {red}+3}<b\;$

の両辺から3を引くと

$a+3-3<b-3\;$

よって

$a<b{\color {red}-3}\;$

となる。

このように、不等式でも移項することができる。

グラフを用いて考えるとき、不等式はグラフ中の領域を表す。領域の境界は不等号を等号に置き換えた部分が対応する。これは、不等号が成立するかどうかがその線上で入れ替わることによっている。（詳しくは数学II 図形と方程式で学習する。）

• 問題

$y>x+1$,$y<2x+1$,$x<3$のグラフ(正しくは「領域」)を描け。

• 解答

$y>x+1$ のグラフ(領域)は次のようになる。ただし、境界は含まない。

1次不等式 y>x+1 が表すグラフ。

$y<2x+1$のグラフ(領域)は次のようになる。ただし、境界は含まない。

1次不等式 y<2x+1 が表すグラフ。

$x<3$のグラフ(領域)は次のようになる。ただし、境界は含まない。

1次不等式 x<3 が表すグラフ。

• 問題

次の不等式を解け。

1. 　　$3x-1\leq 9x-7$
2. 　　$3(x-2)>2(5x-3)$
3. 　　$x+1<{\frac {x-1}{3}}$

• 解答

1. ${\begin{aligned}\quad 3x-1&\leq 9x-7\\3x-9x&\leq -7+1\\-6x&\leq -6\\x&\geq 1\end{aligned}}$
2. ${\begin{aligned}\quad 3(x-2)&>2(5x-3)\\3x-6&>10x-6\\3x-10x&>-6+6\\-7x&>0\\x&<0\end{aligned}}$
3. ${\begin{aligned}\quad x+1&<{\frac {x-1}{3}}\\3x+3&<x-1\\3x-x&<-1-3\\2x&<-4\\x&<-2\end{aligned}}$

連立不等式

いくつかの不等式を組み合わせたものを連立不等式といい、これらの不等式を同時に満たす$x$の値の範囲を求めることを、連立不等式を解くという。

• 問題例

• • 問題

次の連立不等式を解け。

(i)

$\left\{{\begin{matrix}x+2<2x+4\\10-x\geq 3x-6\end{matrix}}\right.$

(ii)

${\begin{cases}x\geq 1-x\\2(x+1)>x-2\end{cases}}$

• • 解答

(i)

$x+2<2x+4$から　$-x<2$

$x>-2$……(1)

$10-x\geq 3x-6$から　$-4x\geq -16$

$x\leq 4$……(2)

(1),(2)を同時に満たす$x$の値の範囲は

$-2<x\leq 4$

(ii)

$x\geq 1-x$から　$2x\geq 1$

$x\geq {\frac {1}{2}}$……(1)

$2(x+1)>x-2$から　$2x+2>x-2$

$x>-4$……(2)

(1),(2)を同時に満たす$x$の値の範囲は

$x\geq {\frac {1}{2}}$

絶対値を含む不等式

絶対値を含む不等式について考えよう。

絶対値$|x|$は、数直線上で、原点$\mathrm {O}$と点$\mathrm {P} (x)$の間の距離を表している。

したがって、$a>0$のとき

$|x|<a\Leftrightarrow -a<x<a$

$|x|>a\Leftrightarrow x<-a\ ,\ a<x$

• 問題例

• • 問題

次の不等式を解け。

(i)

$|x|<5$

(ii)

$|x|\geq 4$

(iii)

$|x-2|\leq 3$

(iv)

$|x+3|>1$

• • 解答

(i)

$|x|<5$

$-5<x<5$

(ii)

$|x|\geq 4$

$x\leq -4\ ,\ 4\leq x$

(iii)

$|x-2|\leq 3$

$-3\leq x-2\leq 3$

$-1\leq x\leq 5$

(iv)

$|x+3|>1$

$x+3<-1\ ,\ 1<x+3$

$x<-4\ ,\ -2<x$