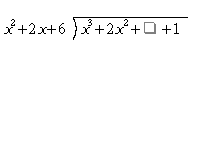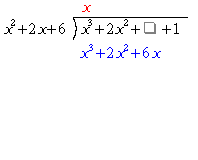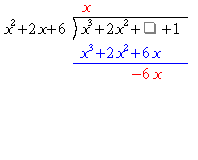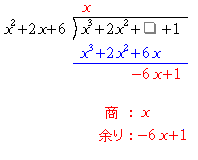高等学校数学II/式と証明・高次方程式

高等学校数学II > 式と証明・高次方程式

---

本項は高等学校数学IIの式と証明・高次方程式の解説である。

式と証明・高次方程式

式と証明

整式の除法、分数式

ここでは、整式の除法と分数式について扱う。整式の除法は、整式を整数のように扱い除法を行なう計算手法のことである。実際に整数の除法と整式の除法には深いつながりがある。整式の因数分解を考えるとそれ以上因数分解できない整式が存在する。この整式を整数でいう素因数のように扱うことで整式の素因数分解が可能になる。この対応は後に詳しく調べられるが、これは指導要領の範囲外である。数学、w:素因数分解などを参照。

上では、整式が整数に対応する性質を持つことを述べた。整数についてはたがいに素な2つの整数を取ることで有理数を定義することが出来る。整式に対しても同じ事が成立ち、そのような式を分数式と呼ぶ。

整式の除法

分数を用いないときには、整数の除法は商と余りを用いて定義された。この時、割られる数Bは商Dと割る数A、余りRを用いて

$B=AD+R$

の性質を満たすことが知られている。整式に対しても似た性質が成立ち、割られる式B(x)が商D(x)と割る式A(x)、余りR(x)を用いて、

$B(x)=A(x)D(x)+R(x)$

と書かれるとき、B(x)が、A(x)に割られたという。この時、整数の除法の性質R<Aに対応して、R(x)の次数<A(x)の次数が成立する。具体例として、x +1を、xで割ることを考える。割る式の次数が1であることから余りの次数は0となり余りは実数である必要がある。また、商がxの関数であると

$B(x)=A(x)D(x)+R(x)$

の右辺でxについて2次の項が現われ左辺と一致しなくなる。よって商は実数である。商をa、余りをrとすると上の式は、

$x+1=ax+r$

となるが、これはa=1,r=1で成立する。よって商1,余り1である。より高次の式に対しても同じ様に答えを定めていけばよい。例として、

$x^{3}\div (x^{2}-1)$

のような式を考える。この場合、

$B(x)=A(x)D(x)+R(x)$

で、B(x)が3次、A(x)が2次であることから、D(x)は1次であり、また、R(x)は2次より小さいことから1次以下の式になる。ここで、D(x)=ax+b,R(x)=cx+dとおくと、

$x^{3}=(x^{2}-1)(ax+b)+(cx+d)$

が得られる。右辺を展開すると、

$x^{3}=ax^{3}+bx^{2}+(-a+c)x+(-b+d)$

が得られるが、両辺が恒等式であることを用いると、a = 1, b = 0, -a +c = 0, -b +d = 0が得られ、結局a=c=1, b=d=0が得られる。

この方法はどの除法に対しても用いることが出来るが、次数が高くなると計算が難しくなる。整数の場合と同様、整式の除法でも筆算を用いることが出来る。上の例を用いて結果だけを書くと、

• 図

のようになる。)右に書かれた式が割られる式であり、)左に書かれた式が割る式である。--の一番上に書かれた式は商であり、整数の割り算同様左に書かれた数から順に割っていく。ここでは次数が大きい項がより先に計算される項である。割られる式の下にある式は商の第1項を割る式にかけて得る式である。ここでは、$x(x^{2}-1)$で、$x^{3}-x$となる。ただし、整数の除法と同様、位をそろえなくてはならない。その後、割られる式から$x^{3}-x$を引き、残った式を新しい割られる式として扱う。ここでは、得た式が割る式よりも低次であることから、これで計算は終了である。

• 問題例
  • 問題

$x^{3}+2x^{2}+1$

、

$x^{4}+4x^{2}+3x+2$

を、

$x^{2}+2x+6$

で割った商と余りを求めよ。

• • 解答

この計算はアニメーションを使って 詳しく表示されている。計算手法は、 整数の場合の筆算と同じような手法が使える。

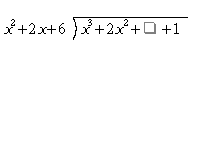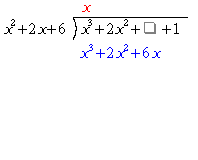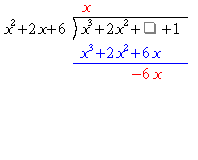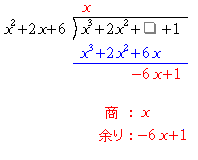計算のアニメーション

$x^{3}+2x^{2}+1=(x^{2}+2x+6)x+(1-6x)$

が得られるので、商

$x$

、余り

$-6x+1$

である。

2つ目の式については、

$x^{4}+4x^{2}+3x+2=(x^{2}-2x+2)*(x^{2}+2x+6)+11x-10$

が得られる。 よって、答は 商

$x^{2}-2x+2$

、余り

$11x-10$

である。

分数式

ここまでで整式を整数のように扱い、整式の除法を行なう方法について述べた。ここでは、整式に対して分数式を定義する方法について述べる。分数式とは、整数に対する分数のように、除法によって生じる式である。ここで、除法を行なう式はどのようなものでも差し支えない。分数式では、分子に割られる式を書き、分母に割る式を書く。例えば、

${\frac {x+1}{x^{2}+4}}$

は、分子x+1、分母:$x^{2}+4$の分数式である。分数式に対しても約分や通分が存在する。約分は共通因数を持った分子分母をもつ分数式で用いられる。この時には分子分母を共通因数で割り、式を簡単にすることが出来る。通分は、分数式の加法の時によく用いられるが、分子分母に同じ整式をかけても分数式が変化しない性質を用いる。分数式の乗法は、分子分母を別々にかければよい。

• 問題例
  • 問題

${\frac {x^{2}-1}{x^{3}-1}}$

を簡単にせよ。また、

${\frac {x+1}{x^{2}+2x+3}}+{\frac {2x+5}{x^{2}+1}}$

を通分せよ。

• • 解答

${\frac {x^{2}-1}{x^{3}-1}}$

について分子と分母を因数分解すると、双方ともに

$x-1$

を因数として含んでいることが分かる。このとき、共通の因数は約分することが必要である。計算された値は、

${\frac {x^{2}-1}{x^{3}-1}}$

$={\frac {(x-1)(x+1)}{(x-1)(x^{2}+x+1)}}$

$={\frac {x+1}{x^{2}+x+1}}$

となる。

次の問題では、

${\frac {x+1}{x^{2}+2x+3}}+{\frac {2x+5}{x^{2}+1}}$

を通分する。 このとき、両辺の分母をそろえる必要があるが、 今回については、単純にそれぞれの分数式の分子と分母に各々の分母をかけて分母を統一すればよい。計算すると、

${\frac {x+1}{x^{2}+2x+3}}+{\frac {2x+5}{x^{2}+1}}$

$={\frac {(x+1)(x^{2}+1)}{(x^{2}+2x+3)(x^{2}+1)}}+{\frac {(x^{2}+2x+3)(2x+5)}{(x^{2}+2x+3)(x^{2}+1)}}$

$={\frac {(x+1)(x^{2}+1)+(x^{2}+2x+3)(2x+5)}{(x^{2}+2x+3)(x^{2}+1)}}$

$={\frac {3x^{3}+10x^{2}+17x+16}{(x^{2}+2x+3)(x^{2}+1)}}$

となる。

等式と不等式の証明

等式がなりたっていることを示すことを 証明とよぶ。

例えば、 ${\sqrt {x^{2}}}=|x|$ を示すことが出来る。 (これは一例として挙げただけで、他にもたくさんの等式がある。) $x>0$ では、成立する。 $x<0$ では、左辺はxとなりそうだが、これは必ず正の数でなくてはいけない。 正の数であって $x^{2}$ の平方根である数はこのとき、 $-x$ である。 また、右辺は必ず正であるが、このとき $x$ は負の数なので、右辺も $-x$ となる。 よって $x<0$ でも、成立する。

• 問題例

• • 問題

次の等式、不等式が成り立つことを証明せよ。
(I)

$(6a+7b)^{2}+(7a-6b)^{2}=(9a+2b)^{2}+(2a-9b)^{2}$

(II)

$x^{2}+10y^{2}\geq 6xy$

• • 解答

(I)
(左辺)$=(36a^{2}+84ab+49b^{2})+(49a^{2}-84ab+36a^{2})=85a^{2}+85b^{2}$
(右辺)$=(81a^{2}+36ab+4b^{2})+(4a^{2}-36ab+81a^{2})=85a^{2}+85b^{2}$
両辺とも同じ式になるから

$(6a+7b)^{2}+(7a-6b)^{2}=(9a+2b)^{2}+(2a-9b)^{2}$

(II)

$(x^{2}+10y^{2})-6xy=x^{2}-6xy+9y^{2}+y^{2}=(x-3y)^{2}+y^{2}$

$(x-3y)^{2}\geq 0,y^{2}\geq 0$

だから

$(x-3y)^{2}+y^{2}\geq 0$

よって、

$x^{2}+10y^{2}\geq 6xy$

2つの数$a$,$b$に対し、${\frac {a+b}{2}}$を相加平均、${\sqrt {ab}}$を相乗平均という。

$a\geq 0,b\geq 0$のとき

${\frac {a+b}{2}}-{\sqrt {ab}}={\frac {a+b-2{\sqrt {ab}}}{2}}={\frac {\left({\sqrt {a}}\right)^{2}-2{\sqrt {a}}{\sqrt {b}}+\left({\sqrt {b}}\right)^{2}}{2}}={\frac {\left({\sqrt {a}}-{\sqrt {b}}\right)^{2}}{2}}$

$\left({\sqrt {a}}-{\sqrt {b}}\right)^{2}\geq 0$であるから、${\frac {\left({\sqrt {a}}-{\sqrt {b}}\right)^{2}}{2}}\geq 0$
したがって　${\frac {a+b}{2}}\geq {\sqrt {ab}}$
等号が成り立つのは、$\left({\sqrt {a}}-{\sqrt {b}}\right)^{2}=0$
すなわち$a=b$のときである。

相加平均と相乗平均

$a\geq 0$ ，$b\geq 0$のとき、 ${\frac {a+b}{2}}\geq {\sqrt {ab}}$ 等号が成り立つのは、$a=b$のときである。

証明では、上の式の両辺に2をかけた$a+b\geq 2{\sqrt {ab}}$を使うことが多い。

• 問題例

• • 問題

$a\geq 0$ ，$b\geq 0$のとき、次の不等式が成り立つことを証明せよ。
(I)

$a+{\frac {1}{a}}\geq 2$

(II)

$(a+b)\left({\frac {1}{a}}+{\frac {1}{b}}\right)\geq 4$

• • 解答

(I)$a\geq 0$であるから、${\frac {1}{a}}\geq 0$
よって　$a+{\frac {1}{a}}\geq 2{\sqrt {a\times {\frac {1}{a}}}}=2$
したがって

$a+{\frac {1}{a}}\geq 2$

(II)

$(a+b)\left({\frac {1}{a}}+{\frac {1}{b}}\right)=1+{\frac {a}{b}}+{\frac {b}{a}}+1={\frac {b}{a}}+{\frac {a}{b}}+2$

$a\geq 0$，$b\geq 0$であるから、${\frac {b}{a}}\geq 0$，${\frac {a}{b}}\geq 0$
よって　${\frac {b}{a}}+{\frac {a}{b}}+2\geq 2{\sqrt {{\frac {b}{a}}\times {\frac {a}{b}}}}+2=2+2=4$
したがって

$(a+b)\left({\frac {1}{a}}+{\frac {1}{b}}\right)\geq 4$

高次方程式

複素数

2乗して負になる数を純虚数とよぶ。これは数直線上にはないことがわかる。 実際、正の数でも負の数でも2乗すると符合が打ち消して正の数になってしまうから である。

特に、 $x^{2}=-1$ の解の片方を $i$ とよぶ。 もう片方は $-i$ となる。iを虚数単位と呼ぶ。純虚数はiに比例する数である。複素数とは、実数と純虚数の和で書ける数のことである。例えば、1+i,2+5i, 9/2 + 7/2 i は複素数である。通常の実数は複素数に含まれる。これは例えば、a(aは実数。)という数が、a + 0iという形に書くことで実数+純虚数の形に書けるからである。

ここでは、更に用語を導入する。ある複素数zに対して、複素数の虚数部の符合を反転させたものを複素数zの共役と呼び、

${\bar {z}}$

$z^{*}$

などと書かれる。

実数同様、複素数にも四則演算が定義される。複素数の演算では、虚数単位iを、通常の文字のように扱って計算する。一般に複素数z,wが、z = a+bi, w=c+diで与えられるとき、(a,b,c,dは任意の実数。)

$z\pm w=(a\pm c)+(b\pm d)i$

が得られる。

• • 問題

複素数

$a=3+i$

$b=4+7i$

について、

$a+b$

$ab$

${\frac {a}{b}}$

を計算せよ。

• • 解答

虚数単位 $i$ は、通常の文字のように扱って計算する。ただし、 $i^{2}$ が出て来たときには、 $i^{2}=-1$ を用いて簡単化する。また、複素数の分数に関しては、分母を実数の形にすることが求められる。

複素数

$a=3+i$

$b=4+7i$

$a+b$

$=(3+4)+i(1+7)$

$=7+8i$

,

$ab$

$=(3+i)(4+7i)$

$=12+21i+4i+7i^{2}$

$=12+25i-7$

$=5+25i$

が得られる。一般に複素数の和や積は再び、複素数の形でかかれる。

最後に

$a/b$

$=(3+i)/(4+7i)$

については、分母を実数で表わさなくてはならない。ここでは、分子と分母の両方に

$4-7i$

をかける。一般に複素数の分数は、分子と分母に分母で、複素数の虚数部の符合を反転させたものをかけ算すると、分母を実数に出来る。このことを用いると、

$a/b$

$=(3+i)/(4+7i)$

$=(3+i)(4-7i)/(4+7i)(4-7i)$

$={\frac {1}{65}}(12+4i-21i+7)$

$={\frac {1}{65}}(19-17i)$

が得られる。

複素数の応用として、ここでは2次方程式の性質について述べる。任意の2次方程式は、解の公式によって解かれることを高等学校数学Iで述べた。しかし、解の公式に含まれる根号の中身が負の数の場合には解が存在しないことに注意する必要がある。一般に、2次方程式

$ax^{2}+bx+c=0$

で、判別式Dが、

$D={\sqrt {b^{2}-4ac}}$

によって定義される。 判別式は、解の公式の根号の中身に等しく、この数の正負によって2次方程式が解を持つかどうかが決まる。Dが負のときにはこの2次方程式は実数の範囲には解を持たない。

しかし、

${\sqrt {-1}}=i$

という量を導入すれば、仮に判別式Dが負の数であったときにも、

${\sqrt {D}}={\sqrt {-|D|}}={\sqrt {-1}}{\sqrt {|D|}}=i{\sqrt {|D|}}$

のように解を書き換えることが出来る。この書き換えによって、判別式Dが負の場合でも、2次方程式の解を定義することが出来るのである。Dが正のときや0のときには、方程式が実数の解を持つことを既に述べた。ここで、実数が複素数に含まれることと考え合わせると、任意のDの値に対して、2次方程式は複素数の範囲で解を持つことがわかる。

• 例

$x^{2}+1=0$

は、 $x=i,-i$ を与える。これは、解が複素数になる例である。

• 問題例

• • 問題

複素数を用いて、 方程式 (1)

$x^{2}+5x+9=0$

(2)

$2x^{2}+5x+8=0$

(3)

$2x^{2}-2x+8=0$

を解け。

• • 解答

解の公式を用いて解けばよい。(1)だけを計算すると、

$x={\frac {1}{2}}(-5\pm {\sqrt {25-4\times 9}})$

$={\frac {1}{2}}(-5\pm {\sqrt {11}}i)$

となる。 他も同じように扱うことが出来る。

以降の解答は、(2)

$x={\frac {1}{4}}(-5\pm {\sqrt {39}}i)$

(3)

$x={\frac {1}{2}}(1\pm {\sqrt {15}}i)$

となる。

2次方程式の判別式

2次方程式 $ax^{2}+bx+c=0$ の解は $x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}$ である。
2次方程式の解の種類は、解の公式の中の根号の中の式 $b^{2}-4ac$ の符号を見れば判別することができる。
この式 $b^{2}-4ac$ を、2次方程式 $ax^{2}+bx+c=0$ の判別式といい、記号 $D$ で表す。

判別式と解の判別

2次方程式 $ax^{2}+bx+c=0$ の判別式 $D=b^{2}-4ac$ について $D>0\Leftrightarrow$ 異なる2つの実数解 $D=0\Leftrightarrow$ 重解 $D<0\Leftrightarrow$ 異なる2つの虚数解

• 問題例

• • 問題

次の2次方程式の解を判別せよ。

(I)

$x^{2}+3\,x-1=0$

(II)

$2\,x^{2}-3\,x+2=0$

(III)

$4\,x^{2}-20\,x+25=0$

• • 解答

(I)

$D=3^{2}-4\times 1\times (-1)=13>0$

だから、異なる2つの実数解をもつ。
(II)

$D=(-3)^{2}-4\times 2\times 2=-7<0$

だから、異なる2つの虚数解をもつ。
(III)

$D=(-20)^{2}-4\times 4\times 25=0$

だから、重解をもつ。

また、2次方程式 $ax^{2}+2b'x+c=0$ のとき、$D=4(b'^{2}-ac)$となる。したがって

2次方程式 $ax^{2}+2b'x+c=0$ の判別式は

${\frac {D}{4}}=b'^{2}-ac$

これを用いて、前の問題(III) $4\,x^{2}-20\,x+25=0$ の解を判別しよう。 $a=4\,,\,b'=-10\,,\,c=25$　であるから

${\frac {D}{4}}=(-10)^{2}-4\times 25=0$

だから、重解をもつ。

2次方程式の解と係数の関係

2次方程式の解と係数の関係

2次方程式 $ax^{2}+bx+c=0$ の2つの解を $\alpha$ ，$\beta$ として、$D=b^{2}-4ac$ とおくと、
$\alpha +\beta ={\frac {-b+{\sqrt {D}}}{2a}}+{\frac {-b-{\sqrt {D}}}{2a}}=-{\frac {b}{a}}$
$\alpha \beta ={\frac {-b+{\sqrt {D}}}{2a}}\times {\frac {-b-{\sqrt {D}}}{2a}}={\frac {b^{2}-D}{4a^{2}}}={\frac {b^{2}-(b^{2}-4ac)}{4a^{2}}}={\frac {c}{a}}$
となる。

解と係数の関係

2次方程式 $ax^{2}+bx+c=0$ の2つの解を $\alpha$ ，$\beta$ とすれば $\alpha +\beta =-{\frac {b}{a}}$ ，$\alpha \beta ={\frac {c}{a}}$

• 問題例

• • 問題

2次方程式 $2x^{2}+4x+3=0$ の2つの解を $\alpha$ ，$\beta$ とするとき、$\alpha ^{2}+\beta ^{2}$ の値を求めよ。

• • 解答

解と係数の関係より、 $\alpha +\beta =-{\frac {4}{2}}=-2$，$\alpha \beta ={\frac {3}{2}}$
$\alpha ^{2}+\beta ^{2}=(\alpha +\beta )^{2}-2\alpha \beta =(-2)^{2}-2\times {\frac {3}{2}}=1$

2数を解とする2次方程式

2つの数 $\alpha$ ，$\beta$ を解とする2次方程式は

$(x-\alpha )(x-\beta )=0$

と表される。左辺を展開して整理すると次のようになる。

与えられた2つの数を解とする2次方程式

2数 $\alpha$ ，$\beta$ を解とする2次方程式は $x^{2}-(\alpha +\beta )x+\alpha \beta =0$

• 問題例

• • 問題

次の2数を解とする2次方程式を作れ。

(I)

$3+{\sqrt {5}}\ ,3-{\sqrt {5}}$

(II)

$2+3i\ ,2-3i$

• • 解答

(I)
和　$(3+{\sqrt {5}})+(3-{\sqrt {5}})=6$
積　$(3+{\sqrt {5}})(3-{\sqrt {5}})=4$　であるから

$x^{2}-6x+4=0$

(II)
和　$(2+3i)+(2-3i)=4$
積　$(2+3i)(2-3i)=13$　であるから

$x^{2}-4x+13=0$

2次式の因数分解

2次方程式 $ax^{2}+bx+c=0$ の2つの解 $\alpha$ ，$\beta$ がわかると、2次式

$ax^{2}+bx+c$

を因数分解することができる。
解と係数の関係 $\alpha +\beta =-{\frac {b}{a}}$，$\alpha \beta ={\frac {c}{a}}$ から、

$ax^{2}+bx+c=a\left(x^{2}+{\frac {b}{a}}+{\frac {c}{a}}\right)=a\left\{x^{2}-(\alpha +\beta )+\alpha \beta \right\}=a(x-\alpha )(x-\beta )$

解と因数分解

2次方程式 $ax^{2}+bx+c=0$ の2つの解を $\alpha$ ，$\beta$ とすると $ax^{2}+bx+c=a(x-\alpha )(x-\beta )$

2次方程式は、複素数の範囲で考えるとつねに解をもつから、複素数まで使ってよいとすると、2次式は必ず1次式の積に因数分解することができる。

• 問題例

• • 問題

複素数の範囲で考えて、次の2次式を因数分解せよ。

(I)

$x^{2}+4x-1$

(II)

$2x^{2}-3x+2$

• • 解答

(I)
2次方程式　$x^{2}+4x-1=0$　の解は

$x={\frac {-4\pm {\sqrt {4^{2}-4\times 1\times (-1)}}}{2\times 1}}={\frac {-4\pm {\sqrt {20}}}{2}}={\frac {-4\pm 2{\sqrt {5}}}{2}}=-2\pm {\sqrt {5}}$

よって

$x^{2}+4x-1=\left\{x-(-2+{\sqrt {5}})\right\}\left\{x-(-2-{\sqrt {5}})\right\}=(x+2-{\sqrt {5}})(x+2+{\sqrt {5}})$

(II)
2次方程式　$2x^{2}-3x+2=0$　の解は

$x={\frac {-(-3)\pm {\sqrt {(-3)^{2}-4\times 2\times 2}}}{2\times 2}}={\frac {3\pm {\sqrt {-7}}}{4}}={\frac {3\pm {\sqrt {7}}i}{4}}$

よって

$2x^{2}-3x+2=2\left(x-{\frac {3+{\sqrt {7}}\;i}{4}}\right)\left(x-{\frac {3-{\sqrt {7}}\;i}{4}}\right)$

高次方程式

3次以上の整式による方程式を考える。 一般に方程式を $f(x)=0$ととる。 ただし、$f(x)$は、任意の次数の整式とする。 ここで、ある実数$a$に対して、

$f(a)=0$

が成り立ったとする。 このとき、整式$f(x)$ は、 $(x-a)$ を因数に持つことが分る。 このことを因数定理と呼ぶ。

• 導出

整式$f(x)$に対して、商$f(x)$、割る式$(x-a)$とする 整式の除法を用いる。このとき、商$g(x)$、 ($g(x)$は、$f(x)$よりも1だけ次数が低い整式である。) 余り$c$($c$は、実数。)とすると、 整式$f(x)$ は、

$f(x)=(x-a)g(x)+c$

と書ける。 ここで、 $c=0$ でないと、 $f(a)=0$ は満たされないが、 このとき、$f(x)$は、$(x-a)$によって割り切れる。 よって、因数定理は成立する。

因数定理を用いることで、より次数の高い整式を因数分解することが 出来るようになる。例えば、3次の整式

$x^{3}-1$

について、$x=1$を代入すると、

$x^{3}-1$

は0となる。よって、因数定理よりこの式は

$(x-1)$

を因数として持つ。

ここで、実際整式の除法を使って計算すると、

$x^{3}-1=(x-1)(x^{2}+x+1)$

が得られる。

• 問題例

• • 問題

因数定理を用いて
(I)

$x^{3}-6\,x^{2}+11\,x-6$

(II)

$x^{3}+x^{2}-14\,x-24$

を因数分解せよ。

• • 解答

(I) 因数分解の結果が(x+整数)の積の形なら、整数は6の因数でなければならない。そのため、$\pm 1,\pm 2,\pm 3,\pm 6$が候補となる。これらについては実際に代入して確かめるしかない。x=1を代入すると、

$1-6+11-6=0$

となるので、(x-1)が因数となる。実際に整式の除法を行なうと、商として$x^{2}-5x+6$が得られるが、これは$(x-2)(x-3)$に因数分解できる。よって答えは、

$\left(x-3\right)\,\left(x-2\right)\,\left(x-1\right)$

となる。
(II) ここでも地道に24の因数を当てはめていくしかない。24の因数は数が多いのでかなりの計算が必要となる。ここでは、-2を代入すると、

$-8+4-14\cdot (-2)-24=0$

となり、(x+2)が因数だとわかる。除法を行なうと、$x^{2}-x-12$が得られるが、(x-4)(x+3)に因数分解できる。答えは、

$\left(x-4\right)\,\left(x+2\right)\,\left(x+3\right)$

となる。

因数分解や因数定理を利用して高次方程式を解いてみよう。

• 問題例

• • 問題

高次方程式
(I)

$x^{3}-8=0$

(II)

$x^{4}-2x^{2}-8=0$

(III)

$x^{3}-5x^{2}+7x-2=0$

を解け。

• • 解答

(I) 左辺を因数分解すると

$(x-2)(x^{2}+2x+4)=0$

したがって$\ x-2=0$　または$\ x^{2}+2x+4=0$
よって

$x=2\ ,\ -1\pm {\sqrt {3}}i$

(II)$\ x^{2}=X\$とおくと、

$X^{2}-2X-8=0$

左辺を因数分解すると

$(X-4)(X+2)=0$

よって　$X=4\ ,\ X=-2$
ゆえに　$x^{2}=4\ ,\ x^{2}=-2$
したがって

$x=\pm 2\ ,\ \pm {\sqrt {2}}i$

(III)$\ P(x)=x^{3}-5x^{2}+7x-2\$とおく。

$P(2)=2^{3}-5\times 2^{2}+7\times 2-2=0$

したがって、$\ x-2\$は$\ P(x)\$の因数である。

$P(x)=(x-2)(x^{2}-3x+1)$

よって　$(x-2)(x^{2}-3x+1)=0$
$\ x-2=0$　または$\ x^{2}-3x+1=0$
したがって

$x=2\ ,\ {\frac {3\pm {\sqrt {5}}}{2}}$