高等学校情報/情報の科学/論理回路と半導体

※ ANDやORの概念については、『高等学校情報社会と情報/検索』を参照せよ。

※ 普通科で習うのは、AND,OR,NOTの論理回路と、半加算器について、である。

はじめに

（※ ダイオードとトランジスタによる論理計算については、普通科の範囲外）

ダイオードという半導体素子を用いた回路により、物理的にANDやORの処理を実行できる。

結論を先に示すと、

である。

説明の都合上、ダイオード回路で説明するが、実際の半導体ではMOS半導体で論理素子を実装している。

しかし、このMOS半導体による説明はやや複雑なので、初学者にむけて、まずダイオードで原理を説明する^[1]。

^ たとえば
淺川毅『コンピュータ工学の基礎』、東京電機大学出版局、2018年9月10日第1版第1刷発行、90ページなど、
でも、ダイオード回路によって論理回路の原理を説明している。

では、まずダイオードについて、学んでいこう。

ダイオード

（※ 普通科の物理IIでも習う。物理のほうでも、ダイオードやトランジスタなどでデジタル波形を作っていることを言及している（※ 数研出版の検定教科書などに記載あり）。）

p型半導体とn型半導体を接合し(pn接合)た物体が、一方向のみに電流を流す。

このような部品をダイオード（diode）という。

p側に正電圧を掛け、n側に負電圧を掛けた時、電流が流れる。

いっぽう、p側に負電圧を描け、n側に正電圧を掛けても、電流が流れない。

回路において、ダイオードが電流を流す向きを順方向（じゅんほうこう）という。順方向とは反対向きを逆方向という。ダイオードの逆方向には、電流は流れない。

このように一方向に流れる仕組みは、ダイオードでは、つぎのような仕組みで、電流が流れるからである。

p側に正電圧を掛け、n側に負電圧を掛けた時

ダイオードのp側に正電圧をかけ、いっぽうn側に負電圧をかけると、p側では正電極の正電圧からホールが反発して接合面へと向かい、いっぽうn側では電子が負電極から反発して接合面へと向かう。そして、接合面で、ホールと電子がであい、消滅する。この結果、見掛け上、正電荷が、正電極から負電極に移動したのと、同等の結果になる。

そして、正電極から、つぎつぎとホールが供給されるので、電流が流れ続ける。

p側に負電圧を描け、n側に正電圧を掛けた時

いっぽう、p側に負電圧を描け、n側に正電圧を掛けた時、p側ではホールは電極（電極には負電圧が掛かってる）に引き寄せられ、接合面からは遠ざかる。同様にn側では電子が電極（正電圧が掛かってる）に引き寄せられ、接合面からは遠ざかる。

この結果、接合面には、余分なホールも余分な電子もない状態となり、よって接合面の付近にはキャリアがなく、この接合面付近のキャリアの無い部分は空乏層（くうぼうそう、depletion layer）と呼ばれる。

そして、それ以降は、ホールも電子も、もうどこにも移動の余地がないので、よって電流が流れない。

このようにして、ダイオードは、P側の電圧が、N側の電圧よりも高い場合にのみ、電流を流す。

ダイオードによる論理計算

AND回路

（※ 普通科の範囲外）

（※　工業高校教科書でも科目『ハードウェア技術』にしか書いてない！）

なぜ、この回路図がAND処理なのか、見ていこう。

まず、図のCは論理計算「A and B」に対応する結果である。

説明の簡単化のため、Aの電圧は0Vか4Vのどちらかを取るとしよう。同様に、Bの電圧は0Vか4Vのどちらかを取るとしよう。（5Vでなく4Vとしたのは、抵抗Rがあるため、電圧が少し下がるからである。べつに4.5Vでもいい。）

さて、AとBの電圧の両方とも4V以上の場合にのみ、Cが4Vになる。

なぜなら、

・もし、AとBの電圧の両方とも4V以上なら、ダイオードが導通しないので電流が流れないから、4Vがほぼそのまま出力Cに伝わる。（抵抗Rでの電圧降下はあるが、充分に無視できるように、回路を設計してあるとする。）

・一方、もし、Aが0Vなら、ダイオードD1が導通する。このとき、オームの法則により、抵抗Rで電圧が5Vぶん低下するので、Cの電圧も0Vになる。よって、Bの電圧が0Vだろうが4Vだろうが、もはやCの電圧は0Vである。

これらの結果を表にまとめると、4Vを「H」として、0Vを「L」とすれば、

入力電圧 A	入力電圧 B	出力電圧 C
H	H	H
H	L	L
L	H	L
L	L	L

となる。

一方、論理計算 A and B とは、

条件 A	条件 B	A and B
真	真	真
真	偽	偽
偽	真	偽
偽	偽	偽

という計算である。AとB が両方とも「真」の場合だけ（つまり英文でいうなら Both A and B の場合）、出力が「真」になるので、AND計算というのである。

「真」をHに対応させ、「偽」をLに対応させれば、

表から分かるように、図の電気回路は、A and B の計算結果と同じである。

よって、ダイオードを用いた回路で、A and B を計算できる。

また、この回路図のように、論理計算のAND計算をできる回路のことをAND回路という。

さて、コンピュータのデジタル信号では、0と1で処理をするのであった。（右図を参照せよ。）

信号処理のため、ダイオードによるORゲートについて、Hを1に置き換え、Lを0に置き換える。

入力 A	入力 B	A and B
1	1	1
1	0	0
0	1	0
0	0	0

これが、0と1からなる数値によってデジタル信号を扱う場合の、AND計算の結果である。

ダイオード回路図を毎回、作図するのは手間なので、下記のような記号を使うべきとされる。

このような記号を論理記号（ろんりきごう、logic symbol）という。

論理回路 AND 。入力00の場合。
論理回路 AND 。入力01の場合。

なお、AND回路の回路図中に抵抗器Rをつける理由は、電圧降下の他にも、ダイオードに、一定以上の大きさの電流が流れ過ぎるとダイオードが壊れるので、電流が流れ過ぎないようにさせるためという役目もある。なので、このような（半導体部品などの）保護の目的のための抵抗器を「保護抵抗」などと言う場合もある。

しかも、ダイオードやトランジスタなどの半導体部品は、たいてい、導通したさいの抵抗値が低い（ダイオードの抵抗値は、ほぼ 0Ω である）ので、保護抵抗をつけてないと、すぐに故障してしまう。

AND回路にかぎらず、一般にダイオードやトランジスタなどの半導体部品をもちいた回路では、半導体部品に一定以上の大きさの電流が流れると故障するので、適切な抵抗値の抵抗器をつける事で、半導体部品を保護する必要がある。

後述するOR回路でも、抵抗器は同様に、半導体部品に大電流が流れ過ぎないように保護している。

OR回路

電圧は、

入力電圧 A	入力電圧 B	出力電圧 C
H	H	H
H	L	H
L	H	H
L	L	L

となる。（Hは電圧が高い状態。Lは電圧が低い状態。）

これに、Hを論理計算の「真」に対応され、Lを「偽」に対応させれば、

条件 A	条件 B	結果 C
真	真	真
真	偽	真
偽	真	真
偽	偽	偽

となる。A か B の少なくともどちらかが「真」であれば（つまり英文でいうなら A or B の場合）、出力が「真」になるので、OR算というのである。なお、AとBが両方とも「真」であっても、少なくとも片方が「真」である事にかわりはないので、AとBが両方とも「真」の場合にも A or B は「真」になる。

表から分かるように、図の電気回路を真偽に置き換えた結果Cは、A or B の計算結果と同じである。

よって、ダイオードを用いた回路で、A or B を計算できる。

また、この回路図のように、論理計算のOR計算をできる回路のことをOR回路という。

さて、コンピュータのデジタル信号では、0と1で処理をするのであった。（右図を参照せよ。）

信号処理のため、ダイオードによるORゲートについて、Hを1に置き換え、Lを0に置き換える。

入力 A	入力 B	A or B
1	1	1
1	0	1
0	1	1
0	0	0

これが、0と1からなる数値によってデジタル信号を扱う場合の、OR計算の結果である。

NOT回路

NOT回路とは、出力に、入力とは反対の結果を出す回路のことである。

つまり、

入力 A	出力 C
H	L
L	H

のような結果を出す回路である。

デジタル信号の 0 , 1 で表記すれば、NOT回路の計算は、次表になる。

入力 A	出力 C
1	0
0	1

次の図のように、トランジスタという素子を使って、NOT計算が可能である。

論理記号

（※ 普通科高校でも習う。普通科の範囲内。）

コンピュータの論理回路は、原理的には、下記のAND回路、OR回路、NOT回路の3つだけの組み合わせで、さまざまな論理を表すことができる。

（※ ただし実際の電子回路は実装上の都合で少し違うが、普通科高校の範囲を超えるので省略する。）

ANDを「論理積」、ORを「論理和」、NOTを「否定」ともいう。

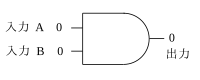
AND回路の論理記号

ダイオード回路図を毎回、作図するのは手間なので、下記のような記号を使うべきとされる。

AND回路の記号は、下図のようになる。

このような記号を論理記号（ろんりきごう、logic symbol）という。

論理回路 AND 。入力00の場合。

論理回路 AND 。入力01の場合。

論理回路 AND 。入力10の場合。
論理回路 AND 。入力11の場合。

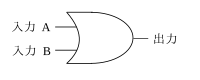
OR回路の論理記号

OR回路の論理記号は、下図のようになる。

論理回路 OR 。入力00の場合。
論理回路 OR 。入力01の場合。

論理回路 OR 。入力10の場合。
論理回路 OR 。入力11の場合。

NOT回路の論理記号

NOTの論理回路の論理記号は、次のようになる。

NOT論理回路。入力＝0 の場合。

NOT論理回路。入力＝1 の場合。

2進数の計算

まず、2進数の1桁どうしの足し算の結果は、次のようになる。

			0
	＋		0
			0

			0
	＋		1
			1

			1
	＋		0
			1

		1
＋		1
	1	0

答えの十の位が1になる場合とは（つまり、くりあがりが起きる場合とは）、入力AとBが両方とも1の場合である。

つまり、くりあがり（carry）の有無を、AND回路を使って書ける。

この論理回路を半加算器（はんかさんき、half adder）という。

図中「C」は、2桁目の数字である。・

図中「S」は、1桁目の数字である。（なお、sum(和)に由来する。）

真理値表で、確認しよう。

まず、加算の真理値表は、次のようになる。

入力		出力
A	B	C	S
1	1	1	0
1	0	0	1
0	1	0	1
0	0	0	0

いっぽう、半加算器の回路図で、入力と出力は、図のようになる。

入力が1と0の場合も、同様に作図できる。

加算の真理値表と、半加算器の計算結果を比べると、一致している。

（※ 全加算器については、普通科高校の範囲外。）

2桁以上の2進数の足し算には、全加算器（ぜんかさんき、full adder）を使う。

全加算器の説明については、省略する。

引き算

コンピュータによる減算（引き算）の方法については、単元『高等学校情報/情報の科学/負数と小数のデジタル表現』で説明する。

コンピュータでは、負数を扱うとき、普通は「補数」（ほすう）と言う技術を使う。じつは「半減算器」という回路も知られているが、しかし普通はコンピュータのマイナスの処理では「半減算器」の回路を使わずに、代わりに「補数」と「加算器」の組み合わせを使うのが普通である。くわしくは上記のリンク先の単元で説明する。

NAND

NANDとは、NOT AND のことであり、ANDゲートの出力にNOTゲートをつけたものである。

※ 実教および第一学習社の「情報I」で掲載を確認。

論理回路は、左図の通り。

さて、NANDを組み合わせるだけで、ANDやORやNOTを作れる。この事は、集積回路をつくる場合、とても重要である。

なぜなら、同じパターンの繰り返しで、論理計算を一通り作れるので、集積度を向上させやすいから、である。

なお、NAND回路を物理的に実現するための部品には、CMOS（シーモス）という電子デバイスを使う。

※ 範囲外: 世間での、まちがった「NAND」の用法

日本の大手の電子部品企業が、USBメモリやフラッシュメモリなどの内部の回路の機構として、NAND回路を利用している事もあり、世間では、USBメモリ→「NAND」という事もある。

しかし、この用法は、正しくない。

なぜなら、まず、USBメモリだけにかぎらず、パソコンの内蔵メモリーの回路の機構としてもNAND回路は用いられるためである。さらに、「NOR」英: not or回路を利用したUSBメモリやフラッシュメモリも存在するし、そのような製品を生産している大手の電子部品企業もある。

なので、もしマスコミ関係者ではない職業の人で、フラッシュメモリ→「NAND」という人が周囲にいれば、そっと間違いを耳打ちしてあげよう。

マスコミの場合は、字数の問題もあり、しかたなく「NAND型フラッシュメモリ」→「NAND」と略する場合もある。

このほか、NORゲートや、XORゲートがある。

※ 日本文教出版がNORを紹介。（wikiでは図は省略する。検定教科書でも図は無い。）

XORは「排他的論理和」ともいう。XORの読みはエックスオアで良い（※第一の見解）。

※ 範囲外: デジタル信号の実現手段は多値論理

「SOS」のモールス符号。よく2値信号の例として説明されるが、考えようには三値信号（「長音」、「短音」、「音なし」の3通り）でもある。

コンピュータでは「0」と「1」の2とおりの数の組み合わせで計算する。しかし、電子部品では、そうではない。

たとえばCD（コンパクトディスク）を考えてみよう。CDのモーターの回転速度が、ある瞬間、ほんの0.01％だけ遅くなったとしよう。

もし、「110001111」みたいに2値信号だけで情報を送信している場合、もし「000」のときにモーターなどの回転が遅くなったとして、「0」状態の滞在時間が長くなってしまい「110000001111」みたいになってしまったら、どうやって訂正するのだろうか？

こういう場合の対策として、信号を2通りではなく、3通り以上で送信するという方法が有効だろう。（実際のCDやDVDが下記の仕組みかどうかは、残念ながら知らない。）

つまり、例えば

「信号なし」 → 「A」

信号値の低い状態（「0」的）に対応する信号 → B

信号値の高い状態（「1」的）に対応する信号 → C

とする。

すると、さきほどの「110001111」は

まず「1A1A0A0A0A1A1A1A1A」と途中変換されて、

さらに「0」→Bとして「1」→Cと変換すれば、

「CACABABABACACACACA」と変換される。

人間が読みやすくすため、「CA CA BA BA BA CA CA CA CA」と書くことにしよう。

すると、もし一時的にモーターなどの回転が遅くなったりしても、「CA CA BA BA BA AAAAA CA CA CA CA」と書くことにしよう。

のように、意味をもたない信号が入ったりするだけなので、これを「1」や「0」と区別できる。

あるいは、もし、「CA CA BA BA BBBBA CA CA CA CA」のようになっても、「BBBBA」を「BA」に訂正すればいい。

もし、「BかCのひとつの信号の代わりには必ずAが来る」と決めておけば、さきほどの例のように「BBBB」と続く場合は速度低下が起きていると検出できる。

このように、3通り以上の値を使って信号を送信するという方法が、速度変化による誤検出を防ぐ方法のひとつとして有効である。

例としてCDをあげたが、おそらく半導体なども似たような仕組みだろう。CPUの周波数だって、ほんの0.00001％くらい、温度や使用年数などによって微妙にズレる可能性があるだろう。

なお、この例であげた信号「A」のように、信号のひくい状態と区別して、「信号そのもののない状態」を表現する値のことを工学用語で「ヌル値」（ヌルち、null value）などという。

われわれが「0」「1」の2値論理だと思ってる信号は、正確には3値以上の信号から、ヌル値の連続などの無意味な部分を除いて、意味をもつ残りの信号を2値の信号に分類したものであろう。

パソコンのキーボードからの文字入力について

パソコンで「aaaaaaaaaa」などと連続して同じ文字を入力するとき、OSにもよるが、よくよく時間に注目してみると、さいしょaボタンを押してから、そのままaボタンを押したままにすると、一文字だけ「a」と表示されるのが0.5秒くらいつづいてから、つづいて0.1秒に1個くらいのペースで次々と「a」が入力されていって、「aaaaaaaaaa」となったりする。

いっぽう、aボタンを押してから、すぐに手を離して、またすぐにaを押すと、0.5秒ほどの待機時間は無く、次の「a」が入力され、「aa」のようになる。

このような文字入力の仕組みでも、入力のない状態を仮に「\null」とすると、

a（0.3秒） \null

（aを押して0.3秒が経過した時点で、aボタンから指を離した）のように入力された場合、パソコンはこれを文字「a」の入力と判別しているわけである。また、\null の状態になった時点で、待ち時間を（0.5秒ではなく）ゼロ秒にリセットしているわけである。なので、次にまた「a」を押すと、待ち時間がゼロなので、すぐに一文字だけまた「a」が追加されるわけである。

このように、入力信号が無い状態を検出することは、キーボード入力文字の検出においても重要である。

[1] たとえば
淺川毅『コンピュータ工学の基礎』、東京電機大学出版局、2018年9月10日第1版第1刷発行、90ページなど、
でも、ダイオード回路によって論理回路の原理を説明している。

[1]