高等学校数学II/図形と方程式

高等学校の学習 > 高等学校数学 > 高等学校数学II > 高等学校数学II/図形と方程式

ここでは直線と円などの性質を座標を用いて考察する。

点と直線

2点間の距離

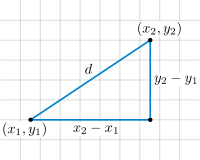
座標平面上の2点 $\mathrm {A} \left(x_{1}\ ,\ y_{1}\right)\ ,\ \mathrm {B} \left(x_{2}\ ,\ y_{2}\right)$ 間の距離 $\mathrm {A} \mathrm {B}$ を求めてみよう。
直線 $\mathrm {A} \mathrm {B}$ が座標軸に平行でないとき、点 $\mathrm {C} \left(x_{2}\ ,\ y_{1}\right)$ をとると

$\mathrm {A} \mathrm {C} =|x_{2}-x_{1}|\ ,\ \mathrm {B} \mathrm {C} =|y_{2}-y_{1}|$

$\triangle \mathrm {A} \mathrm {B} \mathrm {C}$ は直角三角形であるから、三平方の定理より

$\mathrm {A} \mathrm {B} ={\sqrt {\mathrm {A} \mathrm {C} ^{2}+\mathrm {B} \mathrm {C} ^{2}}}={\sqrt {|x_{2}-x_{1}|^{2}+|y_{2}-y_{1}|^{2}}}={\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}$

この式は、直線 $\mathrm {A} \mathrm {B}$ がx軸、y軸に平行なときにも成り立つ。

特に、原点 $\mathrm {O}$ と点 $\mathrm {A} \left(x_{1}\ ,\ y_{1}\right)$ 間の距離は

$\mathrm {O} \mathrm {A} ={\sqrt {x_{1}^{2}+y_{1}^{2}}}$

内分点と外分点

点 $\mathrm {A} (x_{0},y_{0}),\mathrm {B} (x_{1},y_{1})$ と実数 $m,n>0$ に対して、線分 $\mathrm {AB}$ 上の点 $\mathrm {P} (x,y)$ が存在して、$\mathrm {AP} :\mathrm {PB} =m:n$ となるとき、点 $\mathrm {P}$ を $\mathrm {A} ,\mathrm {B}$ を $m:n$ に内分する点という。

また、線分 $\mathrm {AB}$ 上でない点 $\mathrm {P} (x,y)$ が存在して、$\mathrm {AP} :\mathrm {PB} =m:n$ となるとき、点 $\mathrm {P}$ を $\mathrm {A} ,\mathrm {B}$ を $m:n$ に外分する点という。

数直線上の点 $\mathrm {A} (a),\mathrm {B} (b)$ を $m:n$ に内分する点と外分する点を求める。

内分点を $\mathrm {P} (x)$ とする。$a<b$ のとき、 $\mathrm {AP} =x-a,\mathrm {PB} =b-x$ なので、 $m:n=(x-a):(b-x)$ なので、 $n(x-a)=m(b-x)\iff x={\frac {na+mb}{m+n}}$ である。 $a>b$ のときも同様。

次に外分点を求める。外分点を $\mathrm {P} (x)$ とする。$a<b$ で $m>n$ のとき、$x>b$ となるので、 $\mathrm {AP} =x-a,\mathrm {BP} =x-b$ なので、$m:n=(x-a):(x-b)$ なので、$x={\frac {-na+mb}{m-n}}$

これは、$a>b$ または $m<n$ のときも同様。

2次元の場合には、一般に点と点との位置関係は、座標軸に平行でなく、それらの距離の内分は複雑になるように思える。しかし、実際には、内分点や外分点を計算するには、上の公式をx,y の両方向に対して用いればよい。これは、2点をつなぐ線が直線であるので、その直線上である点からの距離が一定の割合となる点をいくつか取ったとき、その点と元の点のx軸方向の座標の変化の割合とy軸方向の座標の変化の割合と直線自身の長さの変化の割合はそれぞれ等しくなるからである。

よって、一般に点$A(x_{0},y_{0}),B(x_{1},y_{1})$を、a:bに内分する点と外分する点は、

内分点

$({\frac {bx_{0}+ax_{1}}{a+b}},{\frac {by_{0}+ay_{1}}{a+b}})$

外分点

$({\frac {-bx_{0}+ax_{1}}{a-b}},{\frac {-by_{0}+ay_{1}}{a-b}})$

$=({\frac {bx_{0}-ax_{1}}{-a+b}},{\frac {by_{0}-ay_{1}}{-a+b}})$

で与えられる。

演習問題

点 $\mathrm {A} (1,0),\mathrm {B} (-4,7)$ を3:1にそれぞれ内分、外分する点を求めよ。

解答

内分点は $\left({\frac {-11}{4}},{\frac {21}{4}}\right)$

外分点は $\left({\frac {-13}{2}},{\frac {21}{2}}\right)$

三角形の重心

3点$\mathrm {A} \left(x_{1},y_{1}\right),\mathrm {B} \left(x_{2},y_{2}\right),\mathrm {C} \left(x_{3},y_{3}\right)$を頂点とする三角形の重心 $\mathrm {G}$ の座標を求めてみよう。
線分$\mathrm {B} \mathrm {C}$の中点$\mathrm {M}$の座標は

$\left({\frac {x_{2}+x_{3}}{2}},{\frac {y_{2}+y_{3}}{2}}\right)$

重心$\mathrm {G}$は線分$\mathrm {A} \mathrm {M}$を2:1に内分する点であるから、$\mathrm {G}$の座標を$(x,y)$とすると

$x={\cfrac {1\times x_{1}+2\times {\cfrac {x_{2}+x_{3}}{2}}}{2+1}}={\frac {x_{1}+x_{2}+x_{3}}{3}}$

同様に

$y={\frac {y_{1}+y_{2}+y_{3}}{3}}$

よって、重心$\mathrm {G}$の座標は

$\left({\frac {x_{1}+x_{2}+x_{3}}{3}},{\frac {y_{1}+y_{2}+y_{3}}{3}}\right)$

直線の方程式

ある点 $(x_{0},y_{0})$ を通って傾きaの直線の式は、 $y-y_{0}=a(x-x_{0})$ で与えられる。これは、傾きがyの変化分$/$xの変化分で表わされ、$y-y_{0}$,$x-x_{0}$はまさに、y,xそれぞれの変化分そのものであることによる。

2点 $(x_{0},y_{0})$ , $(x_{1},y_{1})$ を通る直線は傾きが ${\frac {y_{0}-y_{1}}{x_{0}-x_{1}}}$ で与えられることを用いると、 $y-y_{0}={\frac {y_{0}-y_{1}}{x_{0}-x_{1}}}(x-x_{0})$ で与えられる。

演習問題

それぞれの直線を表わす式を計算せよ。

(i) 傾き-2で、点(-3,1)を通る直線

(ii) 2点(4,3) ,(5,7)を通る直線

解答

$y-y_{0}=a(x-x_{0})$

$y-y_{0}={\frac {y_{0}-y_{1}}{x_{0}-x_{1}}}(x-x_{0})$

を用いればよい。

(i)

$\left[y=-2\,x-5\right]$

(ii)

$\left[y=4\,x-13\right]$

また直線の方程式は一般に $ax+by+c=0$ で表される。

2直線の平行と垂直

2直線の平行、垂直

2直線$y=m_{1}x+n_{1}\ ,\ y=m_{2}x+n_{2}$について 2直線が平行$\Leftrightarrow m_{1}=m_{2}$ 2直線が垂直$\Leftrightarrow m_{1}m_{2}=-1$

• 問題例

• • 問題

点$(1,4)$を通り、直線$y=-2x+3$に平行な直線、垂直な直線の方程式を求めよ。

• • 解答

直線$y=-2x+3$の傾きは$-2$である。
平行な直線の方程式は

$y-4=-2(x-1)$

$y=-2x+6$

垂直な直線の傾きを$m$とすると

$-2m=-1$

$m={\frac {1}{2}}$

よって、垂直な直線の方程式は

$y-4={\frac {1}{2}}(x-1)$

$y={\frac {1}{2}}x+{\frac {7}{2}}$

点と直線の距離

点 $\mathrm {P}$ と直線 $l$ に対し、直線 $l$ 上の点と点 $\mathrm {P}$ の距離の最小値を点と直線の距離という。これは点 $\mathrm {P}$ から直線 $l$ に下ろした垂線 $\mathrm {PH}$ の長さに等しい。

直線 $ax+by+c=0$ と点 $(x_{0},y_{0})$ の距離は

${\frac {|ax_{0}+by_{0}+c|}{\sqrt {a^{2}+b^{2}}}}$

と表される。

証明

点 $\mathrm {P} (x_{0},y_{0})$ と直線 $l:ax+by+c=0\quad a,b\neq 0$ とする。

点 $\mathrm {P}$ から直線 $l$ に垂線を下ろし、垂線の足を点 $R$ とする。

また、点 $\mathrm {P}$ から $y$ 軸に平行な直線を引き、直線 $l$ との交点を点 $\mathrm {S}$ とする。

次に、図のように、直線 $l$ 上の点 $\mathrm {T}$ に対して、直線 $\mathrm {TV}$ が $x$ 軸と平行となり、$\mathrm {TV} =|b|$ となるように点 $\mathrm {V}$ をとり、直線 $\mathrm {VU}$ が $y$ 軸に平行になる点 $\mathrm {U}$ を直線 $l$ 上に取る。

直線 $l$ の傾きは $-{\frac {a}{b}}$ となるので $\mathrm {VU} =|a|$ である。 ここで、$\bigtriangleup \mathrm {PRS} ,\bigtriangleup \mathrm {TVU}$ は直角三角形であり、$\angle \mathrm {PSR} =\angle \mathrm {TUV}$ なので、$\bigtriangleup \mathrm {PRS} \sim \bigtriangleup \mathrm {TVU}$ である。したがって

${\frac {\mathrm {PR} }{\mathrm {PS} }}={\frac {\mathrm {TV} }{\mathrm {TU} }}$

また点 $\mathrm {S}$ の座標を$(x_{0},m)$ とすると、$\mathrm {PS} =|y_{0}-m|$ で、点 $\mathrm {P}$ と直線 $l$ の距離 $\mathrm {PR}$ は、

$\mathrm {PR} ={\mathrm {PS} }\cdot {\frac {\mathrm {TV} }{\mathrm {TU} }}={\frac {|y_{0}-m||b|}{\sqrt {a^{2}+b^{2}}}}$

ところで、点 $\mathrm {S}$ は直線 $l$ 上の点なので、

$m={\frac {-ax_{0}-c}{b}}$

である。これを代入すれば

$\mathrm {PR} ={\frac {|ax_{0}+by_{0}+c|}{\sqrt {a^{2}+b^{2}}}}$

を得る。

ベクトルを使った証明

すでにベクトルを知っているならばこちらの方が簡潔である。

点 $\mathrm {P} (x_{0},y_{0})$ と直線 $l:ax+by+c=0$ とし、点 $\mathrm {Q} (x_{1},y_{1})$ を直線 $l$ 上の点とする。直線 $l$ の法線は ${\vec {n}}:=(a,b)$ で、${\vec {\mathrm {QP} }}=(x_{0}-x_{1},y_{0}-y_{1})$ であるので、直線 $l$ 上の点と点 $\mathrm {P}$ の距離 $d$ は $d=\left|{\vec {\mathrm {QP} }}\cdot {\frac {\vec {n}}{||{\vec {n}}||}}\right|=\left|(x_{0}-x_{1},y_{0}-y_{1})\cdot {\frac {(a,b)}{\sqrt {a^{2}+b^{2}}}}\right|={\frac {|ax_{0}+by_{0}-(ax_{1}+by_{1})|}{\sqrt {a^{2}+b^{2}}}}={\frac {|ax_{0}+by_{0}+c|}{\sqrt {a^{2}+b^{2}}}}$ である。

演習問題

直線 $x-2y-3=0$ と点 $(1,2)$ の距離を求めよ

解答

${\frac {6}{\sqrt {5}}}$

円

円の方程式

中心 $\mathrm {C} (a,b)$ 半径 $r$ の円は、$\mathrm {CP} =r$ となる点 $\mathrm {P}$ の集合である。つまり、 $r={\sqrt {(x-a)^{2}+(y-b)^{2}}}$ となる点 $(x,y)$ の集合である。この方程式の両辺は正なので2乗して

$(x-a)^{2}+(y-b)^{2}=r^{2}$

を得る。これが円の方程式である。

特に原点が中心で半径 $r$ の円の方程式は $x^{2}+y^{2}=r^{2}$ で与えられる。

演習問題

1. 中心 $(2,4)$ 半径 $3$ の円の方程式を求めよ
2. 円 $y^{2}+2\,y+x^{2}-6\,x+5=0$ の中心と半径を求めよ

解答

1. $(x-2)^{2}+(y-4)^{2}=9$
2. $y^{2}+2\,y+x^{2}-6\,x+5=0\iff (x-3)^{2}+(y+1)^{2}=5$ なので中心 $(3,-1)$ 半径 ${\sqrt {5}}$

方程式 $x^{2}+y^{2}+lx+my+n=0$ はいつも円であるとは限らない。

方程式を変形して $(x-a)^{2}+(y-b)^{2}=k$ となるとき

1. $k>0$ のとき方程式は円を表す
2. $k=0$ のとき方程式は1点 $(a,b)$ を表す
3. $k<0$ のとき方程式の左辺は常に正なので、方程式の表す図形はない

円の接線

円$x^{2}+y^{2}=r^{2}$上のある点$(x_{1},y_{1})$で接する接線の方程式は

$x_{1}x+y_{1}y=r^{2}$

で表される。

同様に、円$(x-a)^{2}+(y-b)^{2}=r^{2}$上のある点$(x_{2},y_{2})$で接する接線の方程式は

$(x_{2}-a)(x-a)+(y_{2}-b)(y-b)=r^{2}$

で表される。

円と直線

円と直線の位置関係について大きく次の3つに分類することができる。

1. 円と直線が2点で交わる(直線が円の内部を通る)
2. 円と直線が1点で交わる(直線が円の接線となる)
3. 円と直線は交わらない

一般の円と直線についてそれらの位置関係を分類してみよう。

円 $C:(x-p)^{2}+(y-q)^{2}=r^{2}$ と直線 $l:ax+by+c=0$ について、円 $C$ の中心 $(p,q)$ と直線 $l$ の距離 $d:={\frac {|aq+bq+c|}{\sqrt {a^{2}+b^{2}}}}$ とすると、

1. $r>d$ のとき、円 $C$ と直線 $l$ は2点で交わる
2. $r=d$ のとき、円 $C$ と直線 $l$ は1点で交わる
3. $r<d$ のとき、円 $C$ と直線 $l$ は交わらない

他にも、円の方程式と直線の方程式を連立してその実数解の個数で分類する方法もあるが、位置関係を求めるだけなら上の方法のほうが計算量が少ない。

演習問題

直線 $3x+4y=1$ と円 $(x-3)^{2}+(y+2)^{2}=14$ の交点の座標を求めよ

解答

直線の方程式を $x$ について解き、それを円の方程式に代入すればよい。

答えは $(2,-1),\left(-{\frac {14}{5}},{\frac {7}{5}}\right)$

軌跡と領域

軌跡と方程式

ある条件を満たす点全体がつくる図形を、その条件を満たす点の軌跡という。

• 問題例

• • 問題

2点$\mathrm {A} (1\ ,\ 0)\ ,\ \mathrm {B} (3\ ,\ 2)$から等距離にある点$\mathrm {P}$の軌跡を求めよ。

• • 解答

条件$\mathrm {A} \mathrm {P} =\mathrm {B} \mathrm {P}$より、$\mathrm {A} \mathrm {P} ^{2}=\mathrm {B} \mathrm {P} ^{2}$
$\mathrm {P}$の座標を$(x\ ,\ y)$とすると

$\mathrm {A} \mathrm {P} ^{2}=(x-1)^{2}+y^{2}$

$\mathrm {B} \mathrm {P} ^{2}=(x-3)^{2}+(y-2)^{2}$

だから

$(x-1)^{2}+y^{2}=(x-3)^{2}+(y-2)^{2}$

整理して、

$y=-x+3$

したがって、求める軌跡は、直線$y=-x+3$である。

軌跡を求める手順

1.求める軌跡上の任意の点の座標を$(x\ ,\ y)$などで表し、与えられた条件を座標の間の関係式で表す。 2.軌跡の方程式を導き、その方程式の表す図形を求める。 3.その図形上の点が条件を満たしていることを確かめる。

• 問題例

• • 問題

2点$\mathrm {A} (0\ ,\ 0)\ ,\ \mathrm {B} (3\ ,\ 0)$からの距離の比が$2:1$である点$\mathrm {P}$の軌跡を求めよ。

• • 解答

$\mathrm {P}$の座標を$(x\ ,\ y)$とする。
$\mathrm {P}$を満たす条件は

$\mathrm {A} \mathrm {P} :\mathrm {B} \mathrm {P} =2:1$

すなわち

$\mathrm {A} \mathrm {P} =2\mathrm {B} \mathrm {P}$

これを座標で表すと

${\sqrt {x^{2}+y^{2}}}=2{\sqrt {(x-3)^{2}+y^{2}}}$

両辺を2乗して、整理すると

$x^{2}+y^{2}-8x+12=0$

すなわち

$(x-4)^{2}+y^{2}=2^{2}$

したがって、求める軌跡は、中心が$(4\ ,\ 0)$、半径が$2$の円である。

$m\ ,\ n$を異なる正の数とするとき、2点$\mathrm {A} \ ,\ \mathrm {B}$からの距離の比が$m:n$である点の軌跡は、線分$\mathrm {A} \mathrm {B}$を$m:n$に内分する点と、外分する点を直径の両端とする円である。この円をアポロニウスの円という。

$m=n$のときは、線分$\mathrm {A} \mathrm {B}$の垂直二等分線である。

不等式の表す領域

座標平面上で一次方程式$y=x+k$を満たす点$(x,y)$全体の集合は$k$を$y$切片とする傾き1の直線である。この直線を$l$とする。

一次不等式$y>x+k$を満たす点$(x,y)$全体の集合を考える。

不等式を満たす任意の点$P(x_{1},y_{1})$をとる。$P$を通り$x$軸に垂直な直線を引き、$l$との交点を点$Q(x_{1},y_{2})$とする。このとき${\begin{cases}y_{1}>x_{1}+k\\y_{2}=x_{1}+k\end{cases}}$より$y_{1}>y_{2}$が導かれる。故に、点$P$は直線$l$よりも上側にある。逆に、直線$l$よりも上側にある任意の点$P$は条件を満たす。

同様に、不等式$y<x+k$を満たす任意の点は直線lよりも下側に存在することがわかる。

一般に、変数$x,y$についての不等式を満たす座標平面上の点$(x,y)$全体の集合を、その不等式の表す領域という。領域の境目となる曲線をその領域の境界線という。境界線の方程式は、不等式の不等号を等号に変えたものである。

以上のことから、以下が成り立つ。

直線と領域

直線$l:y=ax+b$について、
①不等式$y>ax+b$の表す領域は直線$l$の上側の部分。ただし、境界線を含まない。
②不等式$y<ax+b$の表す領域は直線$l$の下側の部分。ただし、境界線を含まない。
③不等式$y\geqq ax+b$の表す領域は直線$l$の上側の部分。ただし、境界線を含む。
④不等式$y\leqq ax+b$の表す領域は直線$l$の下側の部分。ただし、境界線を含む。

直線の場合と同様にして、円を境界線とする領域について以下が成り立つ。

円と領域

円$C:(x-a)^{2}+(y-b)^{2}=r^{2}$について、
①不等式$(x-a)^{2}+(y-b)^{2}<r^{2}$の表す領域は円$C$の内部。ただし、境界線を含まない。
②不等式$(x-a)^{2}+(y-b)^{2}>r^{2}$の表す領域は円$C$の外部。ただし、境界線を含まない。

不等号に等号が含まれる場合は境界線を含む。

一般に、以下が成り立つ。

曲線と領域

曲線$y=f(x)$について、
①不等式$y<f(x)$の表す領域は、曲線の上側の部分。ただし、境界線を含まない。
②不等式$y>f(x)$の表す領域は、曲線の下側の部分。ただし、境界線を含まない。

曲線$x=g(y)$について、
③不等式$x<g(y)$の表す領域は、曲線の左側の部分。ただし、境界線を含まない。
④不等式$x>g(y)$の表す領域は、曲線の右側の部分。ただし、境界線を含まない。

連立不等式の表す領域は、各不等式を同時に満たす点全体の集合、すなわち各不等式の表す領域の共通部分である。

例えば、不等式$xy+1<x+y$の表す領域は以下のように求まる。

不等式を変形すると$xy-x-y+1<0$すなわち$(x-1)(y-1)<0$

これは${\begin{cases}x-1<0\\y-1>0\end{cases}}$または${\begin{cases}x-1>0\\y-1<0\end{cases}}$が成り立つことと同値である。

すなわち二つの連立不等式${\begin{cases}x<1\\y>1\end{cases}},{\begin{cases}x>1\\y<1\end{cases}}$が表す領域の和集合が求める領域である。

一つ目の連立不等式の表す領域は直線$x=1$の左側の部分と直線$y=1$の上側の部分の共通部分、二つ目の連立不等式の表す領域は直線$x=1$の右側の部分と直線$y=1$の下側の部分の共通部分なので、求める領域は2直線$x=1,y=1$で区切られた領域の左上・右下の部分である。ただし、境界線は含まない。

領域の考え方は以下のように応用されている。

一次不等式で表される領域内で一次関数の値を最大化（または最小化）する問題を線形計画法という。

（ここに例題）

二つの条件$p,q$について、$p\in P,q\in Q$という集合$P,Q$を設定すると、「$p\implies q$が真」$\iff$「$P\subset Q$」が成り立つ。

条件$p,q$が二変数の不等式で表される場合、領域の考え方を用いて$p\implies q$の真偽を証明できる場合がある。

（ここに例題）

コラム

デカルト

このページの分野のように、数式をつかって座標の位置をあらわして、幾何学の問題を解く手法のことを解析幾何学という。

なお、幾何学という言葉自体は、図形の学問というような意味であり、小学校や中学校で習った図形の理論も幾何学である。

中世ヨーロッパの数学者デカルトが、解析幾何学の研究を進めた。なお、デカルトは、哲学の格言「われ思う、ゆえに我あり」でも有名である。