OpenSCAD User Manual/The OpenSCAD Language
The OpenSCAD Language
[編集]コメント
[編集]OpenSCAD では C++形式のコメントを用いる:
// これはコメント
myvar = 10; // ここからもコメント
/*
複数行のコメント
*/
変数
[編集]変数は以下のように簡単に作ることができる。
例:
myvar = 5 + 4;
文字列
[編集]ダブルクォートとバックスラッシュはエスケープする必要がある (順に\" と \\ )。その他のエスケープ文字は、改行 (\n)、タブ (\t) とCR (\r) である。
NB! この仕様は OpenSCAD-2011.04 からである。古いソースはsed コマンド『sed 's/\\/\\\\/' non-escaped.scad > escaped.scad』で変換できる。
例:
echo("The quick brown fox \tjumps \"over\" the lazy dog.\rThe quick brown fox.\nThe \\lazy\\ dog.");
Output:
ECHO: "The quick brown fox jumps "over" the lazy dog.
The quick brown fox.
The \lazy\ dog."
変数は実行時ではなくコンパイル時に格納される
[編集]注意: OpenSCAD は変数の値の計算を実行時ではなくコンパイル時に行なうので、 一番最後に代入された値がプログラム中のあらゆる参照で有効となる。 変数というより、再定義可能な定数と考えたほうがよいかもしれない。
例:
// 変数 'a' への最後の格納のみが反映される
a = 0;
echo(a);
a = 5;
echo(a);
出力
ECHO: 5 ECHO: 5
このことから、変数は "if" ブロックの中では代入できない:
Example:
a=0;
if (0==a)
{
a=1; // <- この行でエラーになる
}
出力 Compile Error
この振る舞いのスコープは、root (一番上のレベル) または module の呼び出しごとに限られる。 このことから、変数はスコープの外部に影響されることなくモジュール内で再定義できる。 しかしスコープ内でのすべてのインスタンスは、上述のように最後に定義された値になる。
例:
p = 4;
test(5);
echo(p);
p = 6;
test(8);
echo(p);
module test(q)
{
p = 2 + q;
echo(p);
p = 4 + q;
echo(p);
}
Output
ECHO: 9 ECHO: 9 ECHO: 6 ECHO: 12 ECHO: 12 ECHO: 6
これは直感に反するようであるが、面白い使い方ができる。 つまり、デフォルト値を持つようなシェアードライブラリを作成した場合、そのファイルをインクルードしたファイルでは、 単純にデフォルト値を『再定義』つまり上書きするだけで新しい値で使うことができる。
変数の値のスコープをより厳密に定義するには、assign ステートメントを参照。
Getting input
[編集]Now we have variables, it would be nice to be able to get input into them instead of setting the values from code. There are a few functions to read data from DXF files, or you can set a variable with the -D switch on the command line.
Getting a point from a drawing
Getting a point is useful for reading an origin point in a 2D view in a technical drawing. The function dxf_cross will read the intersection of two lines on a layer you specify and return the intersection point. This means that the point must be given with two lines in the DXF file, and not a point entity.
OriginPoint = dxf_cross(file="drawing.dxf", layer="SCAD.Origin",
origin=[0, 0], scale=1);
Getting a dimension value
You can read dimensions from a technical drawing. This can be useful to read a rotation angle, an extrusion height, or spacing between parts. In the drawing, create a dimension that does not show the dimension value, but an identifier. To read the value, you specify this identifier from your script:
TotalWidth = dxf_dim(file="drawing.dxf", name="TotalWidth",
layer="SCAD.Origin", origin=[0, 0], scale=1);
For a nice example of both functions, see Example009 and the image on the homepage of OpenSCAD.
for ループ
[編集]配列要素の値または範囲に基づいて繰り返し実行する。
配列要素の値: for (変数=<配列>) <実行されるもの> - <変数> には配列の値が次々に代入される
範囲: for (変数=<範囲>) <実行されるもの>
範囲: [<初期値>:<終値>] - 初期値から終値まで繰り返す。<終値> は <初期値> より小さくてもよい。
範囲: [<初期値>:<増分>:<終値>] - 初期値から終値まで増分だけ増やして繰り返す。増分は非整数でもよい。
注意: 増分は正の絶対値である必要がある。もし <終値> が <初期値> より小さくとも、増分は絶対値でなくてはならない。
警告: 増分で (<end>-<start>) が割り切れない場合、繰り返しの実際の終値は <end>-(<end>-<start> mod <increment>) となる
(訳注: 範囲を超えることはない。初期値1、終値6、差分2の場合、1、3、5が代入される)。
ループのネスト :
for (変数1 = <範囲または配列>, 変数2 = <範囲または配列> ) <両方の変数を変化させて実行されるもの>
for ループは通常のプログラム同様、ネストできる。ひとつのfor文で両方の繰り返しを実行できる。
| 例1 - 配列要素に基づく繰り返し: | |
for (z = [-1, 1]) // z = -1, z = 1 の2つの繰り返し
{
translate([0, 0, z])
cube(size = 1, center = false);
}
|
 |
| 例2a - 範囲の繰り返し: | |
for ( i = [0 : 5] )
{
rotate( i * 360 / 6, [1, 0, 0])
translate([0, 10, 0])
sphere(r = 1);
}
|
 |
| 例2b - 増分を指定した範囲の繰り返し: |
// 注: 2番めの引数 (この場合 '0.2' ) が増分
// 注: 増分によっては、実際の終値は与えられた終値
// より小さい場合がある。
for ( i = [0 : 0.2 : 5] )
{
rotate( i * 360 / 6, [1, 0, 0])
translate([0, 10, 0])
sphere(r = 1);
}
|
| 例3 - 2次元配列による繰り返し (回転): | |
for(i = [ [ 0, 0, 0],
[ 10, 20, 300],
[200, 40, 57],
[ 20, 88, 57] ])
{
rotate(i)
cube([100, 20, 20], center = true);
}
|
 |
Nested loop example
for (xpos=[0:3], ypos = [0,2,6]) // 3要素の配列を範囲によって4回繰り返す
translate([xpos, ypos, 0]) cube([0.5, 0.5, 0.5]);
forループの交わり (intersection)
[編集]配列または範囲による繰り返しを実行し、描いたものの交わり (intersection) をとる。
注: intersection_for() は、通常のfor() 文と intersection() 文を用いた結果と同じにならない問題があり、対処中である。
パラメータ
- <ループ変数名>
- for ループ内で用いられる変数名。
| 例1 - 範囲の繰り返し: | |
intersection_for(n = [1 : 6])
{
rotate([0, 0, n * 60])
{
translate([5,0,0])
sphere(r=12);
}
}
|
 |
| 例2 - 回転: | |
intersection_for(i = [ [ 0, 0, 0],
[ 10, 20, 300],
[200, 40, 57],
[ 20, 88, 57] ])
{
rotate(i)
cube([100, 20, 20], center = true);
}
|
 |
If 文
[編集]サブツリー内を条件によって評価する。
引数
- 条件となるべきbooleanの式。
例:
if (x > y)
{
cube(size = 1, center = false);
} else {
cube(size = 2, center = true);
}
Assign 文
[編集]変数にサブツリー内での新しい値を代入する。
引数
- (再)代入される変数。
例:
for (i = [10:50])
{
assign (angle = i*360/20, distance = i*10, r = i*2)
{
rotate(angle, [1, 0, 0])
translate([0, distance, 0])
sphere(r = r);
}
}
Update:
このバージョンから値の代入は好きなところでできるため、assign() は必要ない (assign() は後方互換性のために残されている)。
OpenSCAD User Manual/Mathematical Operators
OpenSCAD User Manual/Mathematical Functions
OpenSCAD User Manual/String Functions
cube
[編集]原点の座標に直方体を作る。 centerがtrueの際、原点を中心に作られ、falseの際はx, y, z 共に正の方向に作られる。 引数が下記のパラメータと同じ順ならば、引数の名前を省略し、値だけを入力してもよい。
引数
- size
- 十進数または、長さ3の配列。ひとつの値が与えられた際、その値を辺長として持つ立方体となる。配列が与えられた際、それぞれ、x, y, z方向の長さとなる。初期値は1。
- center
- ブール型。オブジェクトの位置を決める。trueの際、原点を中心に作られる。falseの際はx, y, z 共に正の方向に作られる。初期値はfalse
例:
cube(size = 1, center = false); cube(size = [1,2,3], center = true);
sphere
[編集]原点を中心に球を作る。引数名は省略可である。
引数
- r
- 十進数。球の半径。解像度は大きさや、変数$fa, $fs, $fnに基づく。詳しくはOpenSCAD_User_Manual/Other_Language_Features
- $fa
- 最小分割角度(digree)
- $fs
- 最小分割長さ(mm)
- $fn
- 分割数
例:
sphere(r = 1); sphere(r = 5); sphere(r = 10);
//高解像度の半径2mm球 sphere(2, $fn=100);
// これも高解像度の半径2mm球であるが、 // 軸周りに多数の三角形を生成しない。 sphere(2, $fa=5, $fs=0.1);
cylinder
[編集]座標系の原点に円筒を生成する。 1つの半径 (r) を指定すると円筒になり、2つの異なる半径 (r1, r2) を指定すると円錐になる。
引数
- h 数値。円筒の高さ。デフォルトは1。
- r1
- 数値。円筒底面の半径。デフォルトは1。
- r2
- 数値。円筒上面の半径。デフォルトは1.
- r
- 数値。円筒の上面と底面の半径。太さが均一な円筒を生成する場合はこの値を指定する。デフォルトは1。
- center
- boolean値。trueであれば円筒・円錐の高さの中央が原点となる。
デフォルトは false、つまり円筒の底面 (半径 r1) が原点となる。
- $fa
- 分割角度 (度)。
- $fs
- 分割辺の長さ (mm)。
例:
cylinder(h = 10, r1 = 10, r2 = 20, center = false); cylinder(h = 10, r1 = 20, r2 = 10, center = true); cylinder(h = 10, r=20); cylinder(h = 10, r=20, $fs=6);
polyhedron
[編集]Create a polyhedron with a list of points and a list of triangles. The point list is all the vertexes of the shape, the triangle list is how the points relates to the surfaces of the polyhedron.
Parameters
- points
- vector of points or vertexes (each a 3 vector).
- triangles
- vector of point triplets (each a 3 number vector). Each number is the 0-indexed point number from the point vector.
- convexity
- Integer. The convexity parameter specifies the maximum number of front sides (back sides) a ray intersecting the object might penetrate. This parameter is only needed for correctly displaying the object in OpenCSG preview mode and has no effect on the polyhedron rendering.
Syntax example
polyhedron(points = [ [x, y, z], ... ], triangles = [ [p1, p2, p3..], ... ], convexity = N);
Triangle points ordering When looking at the face from the outside inwards, the points must be clockwise. You can rearrange the order of the points or the order they are referenced in each triangle triple. The order of triangles is immaterial. Note that if your polygons are not all oriented the same way OpenSCAD will either print an error or crash completely, so pay attention to the vertex ordering.
Example, a square base pyramid:
polyhedron(
points=[ [10,10,0],[10,-10,0],[-10,-10,0],[-10,10,0], // the four points at base
[0,0,10] ], // the apex point
triangles=[ [0,1,4],[1,2,4],[2,3,4],[3,0,4], // each triangle side
[1,0,3],[2,1,3] ] // two triangles for square base
);

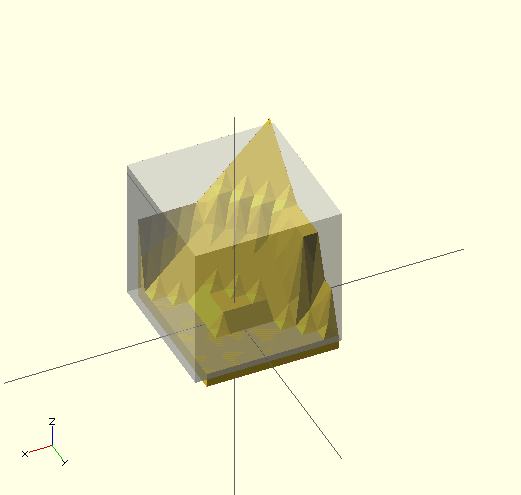
Ordering of triangle points An example of a more complex polyhedron, and showing how to fix polyhedrons with badly oriented polygons.
When you select 'Thrown together' from the view menu and compile the design (not compile and render!) you will see a preview with the mis-oriented polygons highlighted. Unfortunately this highlighting is not possible in the OpenCSG preview mode because it would interfere with the way the OpenCSG preview mode is implemented.)
Below you can see the code and the picture of such a problematic polyhedron, the bad polygons (triangles or compositions of triangles) are in pink.
// Bad polyhedron
polyhedron
(points = [
[0, -10, 60], [0, 10, 60], [0, 10, 0], [0, -10, 0], [60, -10, 60], [60, 10, 60],
[10, -10, 50], [10, 10, 50], [10, 10, 30], [10, -10, 30], [30, -10, 50], [30, 10, 50]
],
triangles = [
[0,2,3], [0,1,2], [0,4,5], [0,5,1], [5,4,2], [2,4,3],
[6,8,9], [6,7,8], [6,10,11], [6,11,7], [10,8,11],
[10,9,8], [0,3,9], [9,0,6], [10,6, 0], [0,4,10],
[3,9,10], [3,10,4], [1,7,11], [1,11,5], [1,7,8],
[1,8,2], [2,8,11], [2,11,5]
]
);

A correct polyhedron would be the following:
polyhedron
(points = [
[0, -10, 60], [0, 10, 60], [0, 10, 0], [0, -10, 0], [60, -10, 60], [60, 10, 60],
[10, -10, 50], [10, 10, 50], [10, 10, 30], [10, -10, 30], [30, -10, 50], [30, 10, 50]
],
triangles = [
[0,3,2], [0,2,1], [4,0,5], [5,0,1], [5,2,4], [4,2,3],
[6,8,9], [6,7,8], [6,10,11],[6,11,7], [10,8,11],
[10,9,8], [3,0,9], [9,0,6], [10,6, 0],[0,4,10],
[3,9,10], [3,10,4], [1,7,11], [1,11,5], [1,8,7],
[2,8,1], [8,2,11], [5,11,2]
]
);
Beginner's tip:
If you don't really understand "orientation", try to identify the mis-oriented pink triangles and then permute the references to the points vectors until you get it right. E.g. in the above example, the third triangle ([0,4,5]) was wrong and we fixed it as [4,0,5]. In addition, you may select "Show Edges" from the "View Menu", print a screen capture and number both the points and the triangles. In our example, the points are annotated in black and the triangles in blue. Turn the object around and make a second copy from the back if needed. This way you can keep track.
Clockwise Technique:
Orientation is determined by clockwise indexing. This means that if you're looking at the triangle (in this case [4,0,5]) from the outside you'll see that the path is clockwise around the center of the face. The winding order [4,0,5] is clockwise and therefore good. The winding order [0,4,5] is counter-clockwise and therefore bad. Likewise, any other clockwise order of [4,0,5] works: [5,4,0] & [0,5,4] are good too. If you use the clockwise technique, you'll always have your faces outside (outside of OpenSCAD, other programs do use counter-clockwise as the outside though).
Think of it as a Left Hand Rule:
If you hold the triangle and the fingers of your hand curls is the same order as the points, then your thumb points outwards.

Succinct description of a 'Polyhedron'
* Points define all of the points/vertices in the shape. * Triangles is a list of triangles that connect up the points/vertices.
Each point, in the point list, is defined with a 3-tuple x,y,z position specification. Points in the point list are automatically given an identifier starting at zero for use in the triangle list (0,1,2,3,... etc).
Each triangle, in the triangle list, is defined by selecting 3 of the points (using the point identifier) out of the point list.
e.g. triangles=[ [0,1,2] ] defines a triangle from the first point (points are zero referenced) to the second point and then to the third point.
When looking at any triangle from the outside, the triangle must list their 3 points in a clockwise order.
OpenSCAD User Manual/Transformations
union
[編集]子ノードの和集合を作る。
Usage example:
union() {
cylinder (h = 4, r=1, center = true, $fn=100);
rotate ([90,0,0]) cylinder (h = 4, r=0.9, center = true, $fn=100);
}
difference
[編集]2番目以降の子ノードを減算する。
Usage example:
difference() {
cylinder (h = 4, r=1, center = true, $fn=100);
rotate ([90,0,0]) cylinder (h = 4, r=0.9, center = true, $fn=100);
}
intersection
[編集]すべての子ノードの共通部分を残す。
Usage example:
intersection() {
cylinder (h = 4, r=1, center = true, $fn=100);
rotate ([90,0,0]) cylinder (h = 4, r=0.9, center = true, $fn=100);
}
render
[編集]常に (even in OpenCSG プレビューモードでも) 子ノードのブーリアンモデルを計算する。
例:
render(convexity = 1) { ... }
| convexity | 整数。convexity (凸度) は、オブジェクトの表面を突き抜ける光線が面と交差する最大の回数。
この変数は、OpenCSGが正しい表示を行なうためだけに必要であり、最終的なレンダリング結果には影響をおよぼさない。 |
この例は、convexity が4である2次元の図形を示している。赤線で示した光線は、図形と4回交差している。 3次元の場合も同様である。大抵の立体では、10程度にしておけばよい。
OpenSCAD User Manual/Modifier Characters
モジュール(他の言語でのマクロ、関数にあたる)は処理の再利用を容易にする。
module hole(distance, rot, size) {
rotate(a = rot, v = [1, 0, 0]) {
translate([0, distance, 0]) {
cylinder(r = size, h = 100, center = true);
}
}
}
この例では、引数 distance、rot、size を設定して呼び出すことにより、このような描画を複数繰り返す場合のプログラムの行数を節約し、 プログラムの可動性を上げる。
呼び出しは、次の例のようにC言語の関数呼び出しに似た方法で、値または数式を渡して行なう。
hole(0, 90, 10);
children
[編集]The child nodes of the module instantiation can be accessed using the children() statement within the module. The number of module children can be accessed using the $children variable.
Parameters
- empty
- select all the children
- index
- integer. select one child, at index value. Index start at 0 and should be less than or equal to $children-1.
- vector
- vector of integer. select children with index in vector. Index should be between 0 and $children-1.
- range
- [<start>:<end>] or [<start>:<increment>:<end>]. select children between <start> to <end>, incremented by <increment> (default 1).
Deprecated child() module
Up to release 2013.06 the now deprecated child() module was used instead. This can be translated to the new children() according to the table:
| up to 2013.06 | 2014.03 and later |
|---|---|
| child() | children(0) |
| child(x) | children(x) |
| for (a = [0:$children-1]) child(a) | children([0:$children-1]) |
Examples
Transfer all children to another module:
// rotate to other center point:
module rz(angle, center=undef) {
translate(center)
rotate(angle)
translate(-center)
children();
}
rz(15, [10,0]) sphere(30);
Use the first child, multiple time:
module lineup(num, space) {
for (i = [0 : num-1])
translate([ space*i, 0, 0 ]) children(0);
}
lineup(5, 65) sphere(30);
If you need to make your module iterate over all children you will need to make use of the $children variable, e.g.:
module elongate() {
for (i = [0 : $children-1])
scale([10 , 1, 1 ]) children(i);
}
elongate() { sphere(30); cube([10,10,10]); cylinder(r=10,h=50); }
arguments
[編集]One can specify default values for the arguments:
module house(roof="flat",paint=[1,0,0]){
color(paint)
if(roof=="flat"){
translate([0,-1,0])
cube();
} else if(roof=="pitched"){
rotate([90,0,0])
linear_extrude(height=1)
polygon(points=[[0,0],[0,1],[0.5,1.5],[1,1],[1,0]],paths=[ [0,1,2,3,4] ]);
} else if(roof=="domical"){
translate([0,-1,0])
union(){
translate([0.5,0.5,1]) sphere(r=0.5,$fn=20);
cube();
}
}
}
And then use one of the following ways to supply the arguments
union(){
house();
translate([2,0,0]) house("pitched");
translate([4,0,0]) house("domical",[0,1,0]);
translate([6,0,0]) house(roof="pitched",paint=[0,0,1]);
translate([8,0,0]) house(paint=[0,0,0],roof="pitched");
translate([10,0,0]) house(roof="domical");
translate([12,0,0]) house(paint=[0,0.5,0.5]);
}
OpenSCAD User Manual/STL Import
OpenSCAD User Manual/Include Statement
Special variables
[編集]All variables starting with a '$' are special variables. The semantic is similar to the special variables in lisp: they have dynamic instead of lexical scoping.
$fa, $fs and $fn
[編集]The $fa, $fs and $fn special variables control the number of facets used to generate an arc:
$fa is the minimum angle for a fragment. Even a huge circle does not have more fragments than 360 divided by this number. The default value is 12 (i.e. 30 fragments for a full circle). The minimum allowed value is 0.01. Any attempt to set a lower value will cause a warning.
$fs is the minimum size of a fragment. Because of this variable very small circles have a smaller number of fragments than specified using $fa. The default value is 2. The minimum allowed value is 0.01. Any attempt to set a lower value will cause a warning.
$fn is usually 0. When this variable has a value greater than zero, the other two variables are ignored and full circle is rendered using this number of fragments. The default value is 0.
When $fa and $fs are used to determine the number of fragments for a circle, then OpenSCAD will never use less than 5 fragments.
This is the C code that calculates the number of fragments in a circle:
int get_fragments_from_r(double r, double fn, double fs, double fa)
{
if (fn > 0.0)
return (int)fn;
return (int)ceil(fmax(fmin(360.0 / fa, r*2*M_PI / fs), 5));
}
Spheres are first sliced into as many slices as the number of fragments being used to render a circle of the sphere's radius, and then every slice is rendered into as many fragments as are needed for the slice radius. You might have recognized already that the pole of a sphere is usually a pentagon. This is why.
The number of fragments for a cylinder is determined using the greater of the two radii.
The method is also used when rendering circles and arcs from DXF files.
You can generate high resolution spheres by resetting the $fX values in the instantiating module:
$fs = 0.01;
sphere(2);
or simply by passing the special variable as parameter:
sphere(2, $fs = 0.01);
You can even scale the special variable instead of resetting it:
sphere(2, $fs = $fs * 0.01);
$t
[編集]The $t variable is used for animation. If you enable the animation frame with view->animate and give a value for "FPS" and "Steps", the "Time" field shows the current value of $t. With this information in mind, you can animate your design. The design is recompiled every 1/"FPS" seconds with $t incremented by 1/"Steps" for "Steps" times, ending at either $t=1 or $t=1-1/steps.
If "Dump Pictures" is checked, then images will be created in the same directory as the .scad file, using the following $t values, and saved in the following files:
- $t=0/Steps filename="frame00001.png"
- $t=1/Steps filename="frame00002.png
- $t=2/Steps filename="frame00003.png"
- . . .
- $t=1-3/Steps filename="frame<Steps-2>.png"
- $t=1-2/Steps filename="frame<Steps-1>.png"
- $t=1-1/Steps filename="frame00000.png"
Or, for other values of Steps, it follows this pattern:
- $t=0/Steps filename="frame00001.png"
- $t=1/Steps filename="frame00002.png
- $t=2/Steps filename="frame00003.png"
- . . .
- $t=1-3/Steps filename="frame<Steps-2>.png"
- $t=1-2/Steps filename="frame<Steps-1>.png"
- $t=1-1/Steps filename="frame<Steps-0>.png"
- $t=1-0/Steps filename="frame00000.png"
Which pattern it chooses appears to be an unpredictable, but consistent, function of Steps. For example, when Steps=4, it follows the first pattern, and outputs a total of 4 files. When Steps=3, it follows the second pattern, and also outputs 4 files. It will always output either Steps or Steps+1 files, though it may not be predictable which. When finished, it will wrap around and recreate each of the files, looping through and recreating them forever.
$vpr and $vpt
[編集]These contain the current viewport rotation and translation - at the time of doing the rendering. Moving he viewport does not update them. During an animation they are updated for each frame.
- $vpr shows rotation
- $vpt shows translation (i.e. won't be affected by rotate and zoom)
It's not possible to write to them and thus change the viewport parameters (although that could be a decent enough idea).
Example
cube([10,10,$vpr[0]/10]);
which makes the cube change size based on the view angle, if an animation loop is active (which does not need to use the $t variable)
You can also make bits of a complex model vanish as you change the view.
The menu command Edit - Paste Viewport Rotation/Translation copies the current value of the viewport, but not the current $vpd or $vpt.
User-Defined Functions
[編集]Define a function for code readability and re-use.
Usage examples:
my_d=20;
function r_from_dia(my_d) = my_d / 2;
echo("Diameter ", my_d, " is radius ", r_from_dia(my_d));
Echo Statements
[編集]This function prints the contents to the compilation window (aka Console). Useful for debugging code.
The OpenSCAD console supports a subset of HTML markup language. See here for details.
Usage examples:
my_h=50;
my_r=100;
echo("This is a cylinder with h=", my_h, " and r=", my_r);
cylinder(h=my_h, r=my_r);
echo("<b>Hello</b> <i>Qt!</i>");
Shows in the Console as
ECHO:Hello Qt!
Render
[編集]Forces the generation of a mesh even in preview mode. Useful when the boolean operations become too slow to track.
Needs description.
Usage examples:
render(convexity = 2) difference() {
cube([20, 20, 150], center = true);
translate([-10, -10, 0])
cylinder(h = 80, r = 10, center = true);
translate([-10, -10, +40])
sphere(r = 10);
translate([-10, -10, -40])
sphere(r = 10);
}
Surface
[編集]Example 1:
//surface.scad surface(file = "surface.dat", center = true, convexity = 5); %translate([0,0,5])cube([10,10,10], center =true);
#surface.dat 10 9 8 7 6 5 5 5 5 5 9 8 7 6 6 4 3 2 1 0 8 7 6 6 4 3 2 1 0 0 7 6 6 4 3 2 1 0 0 0 6 6 4 3 2 1 1 0 0 0 6 6 3 2 1 1 1 0 0 0 6 6 2 1 1 1 1 0 0 0 6 6 1 0 0 0 0 0 0 0 3 1 0 0 0 0 0 0 0 0 3 0 0 0 0 0 0 0 0 0
Result:
Example 2
// example010.dat generated using octave:
// d = (sin(1:0.2:10)' * cos(1:0.2:10)) * 10;
// save("example010.dat", "d");
intersection() {
surface(file = "example010.dat", center = true, convexity = 5);
rotate(45, [0, 0, 1]) surface(file = "example010.dat", center = true, convexity = 5);
}
Search
[編集]Usage Pattern:
"search" "(" ( match_value | list_of_match_values ) "," vector_of_vectors
("," num_returns_per_match
("," index_col_num )? )?
")";
match_value : ( Value::NUMBER | Value::STRING );
list_of_match_values : "[" match_value ("," match_value)* "]";
vector_of_vectors : "[" ("[" Value ("," Value)* "]")+ "]";
num_returns_per_match : int;
index_col_num : int;
The following are some usage examples.
Index values return as list
[編集]| Example | Code | Result |
|---|---|---|
|
1 |
|
[0,4] |
|
2 |
|
[0] |
|
3 |
|
[] |
|
4 |
|
[0,4] |
Search on different column; return Index values
[編集]Example 5:
search(3,[ ["a",1],["b",2],["c",3],["d",4],["a",5],["b",6],["c",7],["d",8],["e",3] ], 0, 1);
Returns:
[2,8]
Search on list of values
[編集]Example 6: Return all matches per search vector element.
search("abc",[ ["a",1],["b",2],["c",3],["d",4],["a",5],["b",6],["c",7],["d",8],["e",9] ], 0);
Returns:
[[0,4],[1,5],[2,6]]
Example 7: Return first match per search vector element; special case return vector.
search("abc",[ ["a",1],["b",2],["c",3],["d",4],["a",5],["b",6],["c",7],["d",8],["e",9] ], 1);
Returns:
[0,1,2]
Example 8: Return first two matches per search vector element; vector of vectors.
search("abce",[ ["a",1],["b",2],["c",3],["d",4],["a",5],["b",6],["c",7],["d",8],["e",9] ], 2);
Returns:
[[0,4],[1,5],[2,6],[8]]
Search on list of strings
[編集]Example 9:
lTable2=[ ["cat",1],["b",2],["c",3],["dog",4],["a",5],["b",6],["c",7],["d",8],["e",9],["apple",10],["a",11] ];
lSearch2=["b","zzz","a","c","apple","dog"];
l2=search(lSearch2,lTable2);
echo(str("Default list string search (",lSearch2,"): ",l2));
Returns
ECHO: "Default list string search ([\"b\", \"zzz\", \"a\", \"c\", \"apple\", \"dog\"]): [1, [], 4, 2, 9, 3]"