データ構造/はじめに
はじめに(英)-
漸近記法(英)-
配列(英)-
リスト構造とイテレーター(英)
スタックとキュー(英)-
木構造(英)-
最小ヒープと最大ヒープ(英)-
グラフ(英)
ハッシュテーブル(英)-
集合(英)-
トレードオフ(英)
データ構造は、コンピュータが膨大なデータを処理・保存するために用いる形式的な構造です。プログラマは、データ構造を利用して、大量のデータを概念的に管理可能な関係に精神的に構造化することができます。例えば、データの検索やソートを高速に行うためにデータ構造を使用することがあります。スタックという概念は、より一般的なデータ構造の限定された形です。このような制限を設けることで、プログラムの推論を容易にすることができます。また、データ構造はアルゴリズムの複雑さを保証するものでもあります。よって、良いソフトウェアを書くためには、その仕事に適したデータ構造を選択することが重要です。
データ構造は、リストに項目を追加したり、キューで最も優先度の高い項目を検索するなど、データグループに対する操作を提供します。また、データ構造が操作を提供する場合、そのデータ構造を「抽象データ型(ADT)」と呼ぶことができます。抽象データ型は、コードの依存関係を最小限に抑えることができるため、コードを変更する必要がある場合に重要です。低レベルの詳細から抽象化されているため、あるデータ構造と別のデータ構造に共通する高次の共通点のいくつかを利用して、一方を他方に置き換えることができます。
プログラミング言語には、整数や浮動小数点数など、コンピュータのプロセッサーがネイティブにサポートするデータオブジェクトを扱うための組み込み型が用意されています。組み込み型は、プロセッサーが実際に提供するものを抽象化したもので、その実行や制限に関する詳細が隠されているからです。
例えば、浮動小数点数を使う場合、主にその値と適用できる演算に関心があります。例えば、斜辺の長さを計算することを考えてみましょう。
let c := sqrt(a * a + b * b)
上記から生成される機械語コードは、これらの値の計算と結果の積算に共通のパターンを使用することになります。実際、これらのパターンは非常に繰り返しが多いので、この冗長性を避け、プログラマが「どのように」計算したかではなく「どのような」値が計算されたかを考えることができるように、高級言語が作られたのです。
ここで、2つの便利で関連した概念が登場します。
- 「カプセル化(Encapsulation)」とは、一般的なパターンを一つの名前でグループ化し、そのパターンをより高度に理解するためにパラメータ化することです。例えば、乗算演算は2つのソース値を必要とし、その2つの値の積を与えられたデスティネーションに書き込みます。この演算は、ソースと1つのデスティネーションの両方によってパラメータ化されます。
- 「抽象化(Abstraction)」とは、ユーザーから実装の詳細を隠すための仕組みです。例えば数字を掛け合わせるとき、私たちはプロセッサーが実際に使用する技法を知る必要はなく、その特性だけを知っていればよいのです。
プログラミング言語は、機械の抽象化であると同時に、機械の内部の詳細をカプセル化するためのツールでもあります。例えば、あるプログラミング言語で書かれたプログラムは、そのプログラミング言語がユーザーを1つのマシンから十分に遠ざけることができれば、複数の異なるマシンアーキテクチャにコンパイルすることができます。
本書では、プログラミング言語が提供する抽象化やカプセル化を更に進めたデータ構造を紹介します。アプリケーションが複雑になると、プログラミング言語の抽象化だけでは低レベルすぎて管理できなくなります。そこで、低レベルの構成要素の上に独自の抽象化を構築し、その上に更に抽象化を重ねることができます。しかし、抽象化を進めるほどに低レベルの実装の詳細にアクセスできなくなります。このようなアクセスの喪失は悪いトレードオフと聞こえますが、実際には非常に有益です。私たちは、目の前の問題を解決することを第一に考え、恣意的な判断よりもそれを優先します。より高次元で考えることができれば、このような重荷から解放されるでしょう。
本書で扱うデータ構造は、値の集合と、その値にアクセスや変更を行う操作の集合を持つ一つのユニットとして考えることができます。データ構造自体は、操作と各操作の特性(内容や所要時間など)の集合として理解できます。
ビッグ・オー表記法は、コンピューターコードの性能を表現する一般的な方法です。この表記法では、メモリ内の項目数と関数の平均性能の関係が生まれます。たとえば、n個のアイテムのセットに対して、O(n)は、特定の関数が平均してn回セット上で動作することを示します。O(1)は、関数が項目の数に関係なく常に一定の数の演算を行うことを示します。この表記法は、アルゴリズムの複雑さを表現するだけであり、関数はより多くの演算を行うことができますが、nの定数倍は慣習的に削除されます。記号 O はドイツ語のOrdnungの頭字にちなみます。
ノード
[編集]最初に確認するデータ構造はノード構造( node structure )です。ノードは、値の単なるコンテナであり、「次の」ノード(nullの場合もあります)へのポインターです。
上記は構造の抽象化です:
一部の言語では、構造はレコードまたはクラスと呼ばれます。他の言語の中には、構造を直接サポートしていないものもありますが、代わりに、他の構造(タプルやリストなど)から構造を構築することができます。
ここでは、ノードに何らかの形式の値が含まれていることだけを考慮しているため、タイプは重要ではないため、そのタイプは「要素」であると単純に言います。一部のプログラミング言語では、タイプを指定する必要はありません(Scheme、Smalltalk、Pythonなどの動的に型付けされた言語のように)。他の言語では、型を整数または文字列に制限する必要がある場合があります(Cのような静的に型付けされた言語のように)。さらに他の言語では、含まれている要素の型の決定は、その型が実際に使用されるまで遅らせることができます(C++やJavaなどのジェネリック型をサポートする言語のように)。これらのいずれの場合でも、擬似コードを独自の言語に翻訳するのは比較的簡単です。
指定された各ノード操作は、非常に簡単に実装できます。
// Create a new node, with v as its contained value and next as
// the value of the next pointer
function make-node(v, node next): node
let result := new node {v, next}
return result
end
// Returns the value contained in node n
function get-value(node n): element
return n.value
end
// Returns the value of node n's next pointer
function get-next(node n): node
return n.next
end
// Sets the contained value of n to be v
function set-value(node n, v)
n.value := v
end
// Sets the value of node n's next pointer to be new-next
function set-next(node n, new-next)
n.next := new-next
return new-next
end
基本的に、我々は構造そのものや低レベルの実装よりも、操作や実装戦略に関心があります。例えば、我々は指定された時間要件に関心があり、それはすべての操作がである時間を要するとするものです。上記の実装は、各操作にかかる時間の長さが一定であるため、この条件を満たしています。定数時間演算を考えるもう一つの方法は、解析がどの変数にも依存しない演算と考えることです(という表記は次章で数学的に定義されます。今のところ、それは単に一定時間を意味すると考えてよい)。
ノードとは値のコンテナであり、他のノードへのポインタのコンテナでもあるから、ノードのデータ構造自体(とその実装)がいかに単純であるかは驚くにはあたらないでしょう。
ノードからチェーンを構築する
[編集]ノード構造は単純ですが、実は固定サイズの整数だけでは計算できなかったことが計算できるようになります。
しかし、その前に、ノードを使う必要のないプログラムを見てみよう.次のプログラムは、入力ストリーム(ユーザーからでもファイルからでもよい)から、ファイルの終端に達するまで一連の数値を読み込み、最大の数値とすべての数値の平均を出力するものである.
program(input-stream in, output-stream out)
let total := 0
let count := 0
let largest :=
while has-next-integer(in):
let i := read-integer(in)
total := total + i
count := count + 1
largest := max(largest, i)
repeat
println out "Maximum: " largest
if count != 0:
println out "Average: " (total / count)
fi
end
ファイルの終端に達するまで一連の数値を読み込んで、最大の数値と、その数値を均等に割った数値の平均を出力するのです。この問題は、最大の数字が最後に入力されたものである可能性がある点が異なります。その数字を除いたすべての数字の平均を計算するのであれば、すべての数字を何らかの方法で記憶しておくことが必要です。変数を使って前の数字を記憶することもできますが、変数が問題を解くのに役立つのは、入力された数字があまり多くない場合だけです。
例えば、ユーザーが入力した状態を保持するために、200個の変数を用意したとします。さらに、200個の変数がそれぞれ64ビットであったとします。たとえプログラムが非常に巧妙であったとしても、異なるタイプの入力に対してのみ結果を計算することができます。これは非常に多くの組み合わせですが、300個の64ビット数のリストでは、適切にエンコードするためにさらに多くの組み合わせが必要になります。(一般に、この問題は線形空間を必要とすると言われています。有限個の変数しか必要としないプログラムは、すべて「定数空間」で解くことができます)。
コーディングを複雑にする制限(変数の数が一定であることなど)を組み込む代わりに、ノードの抽象化の特性を利用すれば、コンピューターが保持できる数の数字を記憶することができるのです。
program(input-stream in, output-stream out)
let largest :=
let nodes := null
while has-next-integer(in):
let i := read-integer(in)
nodes := make-node(i, nodes) // contain the value i,
// and remember the previous numbers too
largest := max(largest, i)
repeat
println out "Maximum: " largest
// now compute the averages of all factors of largest
let total := 0
let count := 0
while nodes != null:
let j := get-value(nodes)
if j divides largest:
total := total + j
count := count + 1
fi
nodes := get-next(nodes)
repeat
if count != 0:
println out "Average: " (total / count)
fi
end
上記で、もし n 個の整数が正常に読み込まれた場合、 make-node を n 個呼び出すことになります。これにはn個のノードが必要であり(各ノードのvalueとnextフィールドを保持する十分なスペースと内部メモリ管理のオーバーヘッドが必要)、メモリ要求はオーダーになります。同様に、このノードの鎖を構築し、再びその鎖を反復するためには、ステップが必要となり、さらにステップが必要となります。
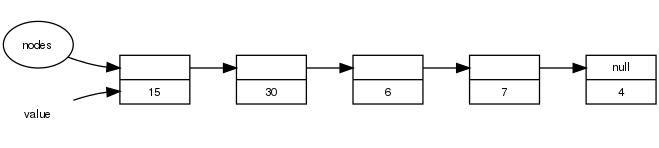
なお、連鎖の中の数字を反復するとき、実際には逆順に見ています。例えば、このプログラムに入力された数字が4、7、6、30、15であるとします。EOFに到達した後、nodesチェーンは次のようになります。
このような連鎖は一般にリンクリスト( linked-lists )と呼ばれます。しかし、私たちは一般的にリスト( lists )やシーケンス( sequences )という言葉で考えることを好んでいます。リストはチェインで作ることができますが、本書ではそれ以外にもいくつかの作り方を紹介します。今のところ、我々はノードの使用方法の一つよりも、ノードの抽象化能力のほうに関心があります。
上記のアルゴリズムでは、make-node、get-value、get-nextの各関数のみを使用します。set-nextを使えば、(順序を逆転させるのではなく)元の順序を保つように、連鎖を生成するアルゴリズムを変更することができます。
[TODO: そのための擬似コード。また、TODO;おそらく、説得力のあります。しかし、あまり高度ではありません。set-valueの使い方を考える必要があります。]
program (input-stream in, output-stream out)
let largest :=
let nodes := null
let tail_node := null
while has-next-integer (in):
let i := read-integer (in)
if (nodes == null)
nodes := make-node(i, null) // construct first node in the list
tail_node := nodes //there is one node in the list=> first and last are the same
else
tail_node := set-next (tail_node, make-node (i, null)) // append new node to the end of the list
largest := max(largest, i)
repeat
println out "Maximum: " largest
// now compute the averages of all factors of largest
let total := 0
let count := 0
while nodes != null:
let j := get-value(nodes)
if j divides largest:
total := total + j
count := count + 1
fi
nodes := get-next(nodes)
repeat
if count != 0:
println out "Average: " (total / count)
fi
end
誘導の原理
[編集]ノードから構築できる連鎖は、数学的帰納法の原理を実証するものです。
|
例えば、という性質は、「個の数を保持する鎖を作ることができる」という文であるとします。これは自然数の性質であり、の特定の値で文が意味をなすからです。
- 5個の数を保持する鎖を作ることができます。
- 100個の数を保持する鎖を作ることができます。
- 1,000,000個の数を保持する鎖を作ることができます。
長さ5、100、100万のチェーンを作成できることを証明する代わりに、一般的なステートメントを証明したいと思います。 上記のステップ2は「帰納的仮説」と呼ばれます。 それを証明できることを示しましょう:
- が成り立つと仮定します。 つまり、要素のチェーンを作成できます。 ここで、が成り立つことを示さなければなりません。
chainが要素チェーンの最初のノードであると想定します。iは、の長さのチェーンを作成するためにチェーンに追加したい数値であると想定します。- 次のコードでこれを実現できます。
let bigger-chain := make-node(i, chain)
- ここに、新しい番号
iがあります。これは、bigger-chainの最初のリンクに含まれる値になります。chainに要素がある場合、bigger-chainには要素が必要です。
Step 3 above is called the Base Case, let's show that we can prove it:
上の手順3を基本ケース( Base Case )と呼びますが、これが証明できることを示しましょう。
が成立することを示す必要があります。つまり、1つの要素からなる連鎖を作ることができることを示す。
- 以下のコードがこれを実現してくれます。
let chain := make-node(i, null)
帰納法の原理は、「要素の鎖をのすべての値に対して作ることができることを証明した」ということです。どうしてそうなるのでしょうか。帰納法を考えるのに最も良い方法は、実は無限の証明を記述するための公式を作る方法であるということでしょう。ベースケースであるに対して文が成り立つことを証明したら、その事実に帰納的仮説を適用してが成り立つことを示すことができるのです。 が成り立つことがわかったので、再び帰納的仮説を適用して が成り立つはずであることを示せばよい。この原理は、このようなことを繰り返しても止められないので、すべての場合について成り立つと考えるべきだというものです。
帰納法は奇妙な証明方法のように聞こえるかもしれませんが、非常に有用なテクニックです。このテクニックが便利なのは、「すべてのに対してが成り立つことを証明せよ」というような難しそうな文を、より小さくて証明しやすい二つの文に分割できる点です。一般に、基本ケースは一般的な文ではないので、証明は簡単です。証明作業のほとんどは通常、帰納的仮説にあり、ケースの証明に「くっつける」ためにステートメントを再定式化する巧妙な方法がしばしば必要になることがあります。
ノードの含まれる値を基本ケースとし、ノードの次のポインタを帰納的仮説と考えることができます。数学の帰納法のように、任意の数の要素を格納するという難しい問題を、1つの要素だけを格納し、さらに別の要素にアタッチする機構を持つという簡単な問題に分解することができるのです。
総和の帰納法
[編集]次に考える帰納法の例は、より代数的な性質を持っています。
という公式が与えられ、この公式が最初の個の数の和を与えることを証明したいとしましょう。最初の試みとして、これが1について正しいことだけを示そうとするかもしれません。
- ,
2 について
- ,
3 について
しかし、この証明と呼ばれるものは、書き出すと無限に長くなることにすぐに気がつくでしょう。この証明を実行し、最初の10億個の数に対して正しいことを示したとしても、それが10億と1億、あるいは1千億の数に対して正しいとは限らないのです。これは、帰納法が有効であることを強く示唆しています。
与えられた公式が本当に最初のn個の数の和を与えることを、帰納法を用いて証明したいとします。まず、基本ケースを証明します。つまり、n = 1のときに真であることを示さなければなりません。これは比較的簡単で、変数nに1を代入すれば、()が得られ、n = 1のときにこの式が正しいことがわかります。
さて、次は帰納的なステップです。この式がjについて成り立つなら、j+1についても成り立つことを示さなければなりません。別の言い方をすれば、1から(j)までの和がであることをすでに証明したと仮定して、1から(j+1)までの和がであることを証明したいのです。なお、この2つの式は、nをそれぞれ(j)と(j+1)に置き換えただけで出てきたものです。
この帰納的ステップを証明するために、まず、1からj+1までの和を計算するには、1からjまでの和を計算し、それにj+1を加えればよいことに注意してください。1からjまでの和を求める式が既にあるので、それにj+1を加えると、このような新しい式が得られます。 となります。ですから、実際に証明を完成させるには、 を示せば良いのです。
上の式が正しいことは、いくつかの簡略化した手順で示すことができます。