中学校理科第1分野/仕事とエネルギー

化学変化とイオン

中学校理科第1分野
仕事とエネルギー

いろいろなエネルギー

力の合成と分解

力の合成

同じ物体に2つの力が働くとき、右図のように、それを一つの大きな力に置き換えることができる。これを「力の合成」といい、また、得られた力の向きと大きさは平行四辺形の対角線となり、また、得られた力を合力（ごうりょく）という。

合力は、計算によって求める事もできるが、ほかにも、作図によって求める事もできる。

合わせる2つの力が同じ向きの場合は、下図のように、2つの力矢印の長さを足し合わせた結果になる。

いっぽう、合わせる2つの力が逆向きの場合は、大きいほうの矢印から小さいほうを引いた、長さの差の力になる。

力の分解

力の合成とは逆に、ひとつの力を複数の力に分解する事もでき、これを「力の分解」といい、また分解によって得られた力を分力（ぶんりょく）という。右図では F₁ および F₂ が、それぞれ分力である。

中学理科では平面上の力を考えているので、2つの力に分解することになる。

力の分解では、まず、分解先の向きとなる、2つの向き（図では a および b で表している）を決める（自由に決めて良い）。

そして、そのa , b の向きに平行な平行四辺形を、図のように書くことで、分力を作図的に決められる。

※ 言葉で分力の書き方を説明するのは難しいので、図を見て理解してほしい。

斜面上の物体に働く力

摩擦の無い斜面上では、そこにある物体には、重力と垂直抗力が図のように働く。それ以外の力は働いていない。

重力のうち、斜面に垂直な分力は、垂直抗力と打ち消しあう。このため、斜面をすべる物体は、斜面から浮びあがったりもしなければ、斜面の地下深くに沈んだりもしない。

そして、重力のうち、斜面に平行で斜め下向きの分力によって、物体は加速していく。

下図のように、斜面の傾きが大きくなればなるほど、斜面に平行で斜め下向きの分力は大きくなる。そのため、斜面の傾き大きいほど、台車は、すばやく斜面をすべり落ちていく。

瞬間の速さと平均の速さ

速さ

速さとは、単位時間（1秒、1分、1時間）あたりの移動距離（m、km）のことである。速さの単位は m/s や km/h など, 長さの単位を時間の単位で割ったような単位である。

瞬間の速度

電車で、「時速100キロメートル」といっても、止まっていた電車がいきなり時速100キロメートルで運転を始めるわけではない。

時速10キロメートル、時速20キロメートル、時速30キロメートル、・・・としだいに加速していって、最終的に時速100キロメートルまで速さを上げていくわけである。

実際には、電車は、なんらかの事情で、またある時は減速したりするが（たとえばカーブの近くでは速さを落すだろう）、またある時は加速したりする。

電車や自動車などのスピードメーター（速度計）には、その各瞬間の速さが表示されてるだろう。

このように、各瞬間ごとの速さを、瞬間の速さ(しゅんかんのはやさ)という。

瞬間の速さは、その瞬間を時間的中点とする区間の平均の速さに等しい。

平均の速度

さて、駅から次の停車駅までの区間の全体的な速さを知りたい場合、そのような各時点での速さでは不便だろう。

たとえば、東北新幹線が、東京駅から新青森駅までの約700kmを、およそ3時間で到着したとしよう。

この東京〜新青森の間での瞬間の速さは、途中の駅で停車したりなどで、瞬間の速さはどんどん変わる。

しかし、最終的に、約700kmの距離を3時間で走行したわけだから、

(700 km) ÷ (3 h) ＝ 233.3333・・・km/h

という計算により、およそ 233 km/h で電車が走行した事が分かる。

このように、区間全体で判断した速さのことを平均の速さという。

運動の規則性

慣性の法則

水平でなめらかな床の上に、ピンポン玉やビー玉などを置いて、手で押すと、しばらく、ほぼ同じ速度で転がりつづける。摩擦があるので、しだいに減速していき、最終的には止まる。

なにも、ボールのように転がる物質でなくても、たとえば、ドライアイスをなめらかな床の上に置いて、ドライアイスをおし動かすと（ゴム手袋をすること。けっして直接はさわらないように）、しばらくドライアイスはそのまま同じ速度で進みつづける。

これは、ドライアイスが出る気体（二酸化炭素）が、床とドライアイスのあいだに入りこむことにより、摩擦が減るからである。

ドライアイスにかかる力には、重力と抗力(こうりょく)があるが、それらの力の方向はどれも、運動の方向とはちがう方向である。

なので、また、ドライアイスにかかる力の合力はゼロである。つまり、図のように摩擦のない水平面の上ですべる物体では、図のように重力と抗力の合力はゼロである。

さて、このように、滑りやすい物体を、地面に滑らせ、その様子を観察する実験を行なう。このとき、物体は向きも速さも変えずに動き続ける。この様な運動を等速直線運動(とうそくちょくせんうんどう)と呼ぶ。

等速直線運動のグラフ。時間と距離。
等速直線運動のグラフ。時間と速度。

運動している物体は、受けている力の合力がゼロである場合、向きと速さを変えずに運動を続ける（静止状態も「速さ0の運動」としてこれに含まれる）。この法則を慣性の法則(かんせいのほうそく)という。

仕事と仕事の原理、仕事率

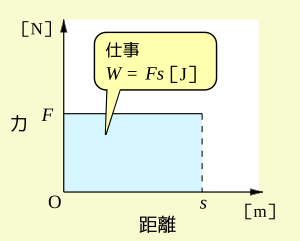
理科では、物体に力を加えて、その力の向きに動かしたとき、仕事(しごと)（英語: work）をしたという。

仕事は、力の大きさと力の向きに動いた距離との積のことである。

仕事＝力 × 力の向きに動いた距離

仕事の単位は, 力の単位に距離の単位をかけたものである。力の単位としてN (ニュートン)を用い, 距離の単位としてm (メートル)を用いた場合の仕事の単位は N m となり, これはJ (ジュール)という名前がついている。

単位時間あたりにする仕事を仕事率(しごとりつ)（英語: power）という。

仕事率＝仕事 ÷ かかった時間

仕事率の単位は, 仕事の単位を時間の単位で割ったものである。仕事の単位としてJ (ジュール)を用い, 時間の単位として秒を用いた場合の仕事率の単位は J/sとなり, これはW(ワット)という名前がついている。

仕事の原理

動滑車やてこなどの道具を使った場合、物体を動かすのに必要な力は小さくなるが、力をはたらかせる距離は大きくなり、仕事は道具を使わない場合と変わらない。このことを仕事の原理'(しごとのげんり)という。

位置エネルギー

仕事の概念を用いて、物体のもつ位置エネルギーが計算できる。質量Mの物体の重さは、重力加速度をg(≒9.8 m/s²)とすれば、Mgなので、位置エネルギーの基準を地面を0とすれば、地面から高さhにある物体の位置エネルギーUは、

位置エネルギー = Mg × h =Mgh

となる。たとえばM=2 kg, h=3 mの場合, 位置エネルギーは,

位置エネルギー = 2 kg × 9.8 m/s² × 3 m = 59 J

となる。ここで、kg m²/s² という単位は、Jという単位と同じである。

仕事率

機械の能力をしりたい時、単位時間あたりにどれだけの仕事ができるかを知りたいときがある。たとえば、モーターを使うときなど、そうだろう。

そこで、仕事率(しごとりつ)が、次の式で定義されており、その単位はワット（記号: W）である。

1秒間に1J（ジュール）の仕事をするのが、1W（ワット）である。つまり、W（ワット）はJ/s（ジュール毎秒）と同じ内容であるが、習慣的にWと書くのが一般である。

仕事率の単位の「ワット」（記号 W）は、電力の単位の「ワット」(記号 W)と同じ単位である。

もし読者がすでに「エネルギー」という量を習ってれば、ワット（W）とは、1秒間あたりに使われるエネルギーの大きさを表す単位ことである。

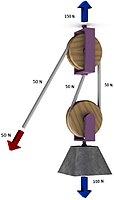
参考:滑車

滑車とは

滑車（かっしゃ）とは、中央に1本の軸を持つ自由回転可能な円盤（索輪）と、その円盤（索輪）を支持して他の物体に接続するための構造部とで構成される機構であり、円盤（索輪）外周部に接する棒状物または索状物の方向を案内する目的のほか、索状物の張力を他の物体に伝達したり　索状物へ張力を与える目的に用いる器具である。

ロープ、ケーブル、ベルト、あるいは鎖などの柔軟性を持った索状物を円盤の周囲にかけて使う場合には、円盤外周に沿って2つのフランジとその間に溝を設けて索状物が逸脱しないようにするのが一般的である。力の方向を変えたり、引張力を伝達するだけではなく、機械的倍率を向上させるのにも多用されている。5種類ある単純機械の1つである。英語では複数の滑車を組み合わせた装置を "block and tackle" と呼ぶが、日本語では「滑車装置」あるいは「複滑車」「組み合わせ滑車」などと呼ぶ。

取付方法の種類

滑車には取付方法により二つの呼称がある。

　　　　　　定滑車
　　　　　　動滑車

定滑車(ていかっしゃ): 滑車の軸が固定されている。すなわち、軸はその場に固定されているか、何らかの形で繋ぎとめられている。定滑車はロープにかかる力の方向を変えるのに使われる。ロープの重さを考えない場合、定滑車の機械的倍率は1である。すなわち、ロープの両端にかかる力は同じである。
動滑車(どうかっしゃ): 滑車の軸は固定されていない。すなわち、その軸は自由に移動できる。滑車とロープの重さを考えない場合、動滑車は機械的倍率を2にする。ロープの一端が固定されており、もう一方の端を引っ張るとその力の2倍の重さの物体を持ち上げることができる。
複滑車(ふくかっしゃ): 定滑車と動滑車を組み合わせた滑車装置。それぞれの軸に複数の滑車があるものを block and tackle と呼び、さらに機械的に有利である。複合滑車で物を持ち上げる際の機械的倍率は2より大きい。

動作原理

図 1 - 滑車の方程式の基本。滑車の軸にかかる力 F は、その滑車を支えている線（ロープ）の両端にかかる張力の総和と等しく、平衡状態では両端の張力は等しい。
図 2 - 単純な滑車システム。単一の動滑車に重量 W の錘が釣り下がっている。線の両端にかかる張力は W/2 となる。したがって機械的倍率は2である。
図 2a - もう1つの単純な滑車システム。この場合、錘を引き上げる力が下に引っ張る力に変換されている。
図 2a を block and tackle で実装する場合

滑車装置の最も単純な理論では、滑車と線（ロープ）に重さがないと仮定し、摩擦によるエネルギー損失もないと仮定する。また、引っ張っても線は伸びないと仮定する。

平衡状態では、動滑車にかかる力はゼロとする。すなわち、動滑車の軸にかかる力は両側の線に等しく分散して伝わることを意味する。これを示したのが図1である。線が平行でない場合でもそれぞれの線の張力は等しいが、方向が異なるためベクトルとして表した力の総和がゼロになる。

次に、錘（負荷）の重量とそれが移動した距離の積は、線を引っ張る力（張力）と引っ張った長さの積に等しい。持ち上げた重さを引っ張った力で割った値が滑車装置の機械的倍率である。

このように、滑車装置は、なされる仕事（しごと）の量を変化させない。仕事は、力と距離の積である。滑車は力が少なくて済む代わりに、距離を犠牲にしている。少ない力で負荷を持ち上げることができるが、所定の高さまで持ち上げるにはより長く引っ張る必要がある。

図2では、動滑車によって重量 W を半分の力で持ち上げることを可能にする。力（図1の赤い矢印）は線の両側に等しくかかり、その一方は天井に固定されている。この単純な装置では、力の方向と重量が移動する方向は同じである。この場合の機械的倍率は2である。重量を引き上げるのに必要な力は W/2 だが、所定の高さまで引き上げるのに2倍の長さの線を引き上げる必要がある。したがって、全体としてなされる仕事（力×距離）は同じである。

図2aでは2つ目の滑車（定滑車）が追加されており、単に力の方向を反転させている。機械的倍率は変化しない。

図 3 - 動滑車と定滑車で錘 W を吊り下げている滑車システム。それぞれの線にかかる張力は W/3 となる。機械的倍率は3。
図 3a - 図 3 と同様だが、引っ張る方向を下に変換している。機械的倍率は3のままである。
図 4a - さらに複雑なシステム。それぞれの線にかかる張力は W/4 となる。機械的倍率は4。

図 4b - 図 4a と同等な実装例 (block and tackle)。定滑車と動滑車それぞれについて、軸を共通化している。

定滑車を追加することで機械的倍率を向上させることもできる。図3では、定滑車を追加することで機械的倍率が3になっている。それぞれの線の張力は W/3 で、それぞれの滑車の軸にかかる力は 2W/3 である。図2aのようにさらに定滑車を追加することで力の方向を反転させることができるが、機械的倍率は変わらない。それを図3aに示す。

このように理想的な滑車を追加していけば、機械的倍率をどんどん向上させることができる。実際には滑車を増やせばその重量もかかるし、摩擦も増大する。したがって、現実の滑車装置には使用可能な滑車数の限界がある。図4aには機械的倍率が4の滑車装置を示している。天井への固定箇所がまとめられ、動滑車が1つの軸でまとめられた実用的な実装を図4bに示す。

滑車がすくない方が効率がよい場合もある。複滑車ではそれぞれの滑車やロープにかかる力が分散される点が最大の利点であり、それによって滑車やロープの耐えられる荷重を抑えつつ、大重量を持ち上げることができる。組み合わせ方によっては、滑車やロープにかかる力がそれぞれの場所で異なることもある。block and tackle では基本的にロープは1本であり、定滑車と動滑車をそれぞれ同じ軸に実装可能という利点がある。　

斜面での仕事

※ 高校物理から図を借用しています。

図のように、傾き θ の斜面があるとしよう。計算の簡単化のため、斜面は滑らかであるとして、摩擦は無いとしよう。また、0° ＜ θ ＜ 90° としよう。

この場合、物体を鉛直方向に h［m］だけ高い場所に上げる仕事を計算しよう。

まず、物体を動かすのに必要な力は、斜面を用いた場合、図から分かるように、

mg\sin \theta

である。

※ なお、sinは「サイン」と読む。θは「シータ」と読む。sinθは「サインシータ」と読む。

しかし、高さhまで上げるために必要な、斜面の距離は、

{\frac {h}{\sin \theta }}

である。

結局、仕事 W は

W=mg\sin \theta \cdot {\frac {h}{\sin \theta }}=mgh

となり、仕事は同じである。

エネルギーとは

すでに、物体の運動は、物体に力が働いたときだけ変化することを見た。ここでは、物体を運動させたり変化させたりすることができる量を、その物体が持つエネルギーと呼ぶ。運動している物体は、それが静止しているボールなどの物体に衝突することによってボールを動かせるので、運動する物体もエネルギーを持っている、運動している物体の、運動によるエネルギーを運動エネルギー（うんどうエネルギー、kinetic energy）という。

さまざまな実験の結果によると、物体の運動エネルギーの公式は、物体の速さを v ［m/s］とし、その物体の質量を m ［kg］としたとき、その物体の運動エネルギーをK［J］とすると、運動エネルギーの公式は

K={\frac {1}{2}}mv^{2}

である。

このように、運動エネルギーは、速さの2次式になる。

なので、たとえば、自動車が時速30kmで走行しているときと、時速60kmで走行しているときとでは、速度が2倍になってるので、運動エネルギーは4倍になっている。

これが、自動車でスピードの出しすぎが危険な理由のひとつである。

運動エネルギーを考えるときには物体の速度の大きさだけに注目し、速度の方向は考えないことに注意が必要である。ここで、あるエネルギーを持った物体は他の物体に衝突することで、持っているエネルギーを衝突した物体に与えることが出来る。このように、ある物体が持つエネルギーは他の物体に与えることが出来る。

いっぽう、物体の衝突の際には、音が発生することがある。音は上で述べた通り空気の振動であるので、空気自身も振動を行なうために、速度を持たなければならず、エネルギーを持つことがわかる。この時には、もともと物体が持っていたエネルギーは、他の物体に移っただけでなく、音として放出されたということが出来る。

このように、ある物体が持っているエネルギーは、他の物体のエネルギーになることや全く違った種類のエネルギーとなることが知られている。エネルギーの種類としては、運動エネルギー（うんどうエネルギー）、位置エネルギー（いちエネルギー）、電気エネルギー（でんきエネルギー）、熱エネルギー（ねつエネルギー）などがある。

力学的エネルギー

ふりこの運動では、位置的な高さがいちばん高い状態になったとき、速度が0である。いっぽう、高さの一番ひくい状態のとき、速度が最大の状態なので、運動エネルギーも最大である。

これは、一番高いときと低いときとの位置エネルギーの差が、運動エネルギーに変わった事と、同等である。

ふりこは、もし摩擦や空気抵抗（くうきていこう）を無視すれば、振り子はずっと振れつづけるので、振り子はいちばん高さの高い状態と低い状態とを何度もずっと交互（こうど）にくりかえしつづける。

この振り子の動きについて、高さ最大の状態と速度最大の状態とのくりかえしの現象（げんしょう）を、エネルギーの考えから見れば、つまり、位置エネルギーと運動エネルギーは、交互に移りかわることができる。

そして、エネルギーの形が位置エネルギーから運動エネルギーに変化しても、あるいは運動エネルギーから位置エネルギーに変化しても、両方のエネルギーを足し合わせた和（＝位置エネルギー＋運動エネルギー）は、変化しない。

ある物体について、位置エネルギーと運動エネルギーとの和を、力学的エネルギーという。

つまり、ある物体について、その物体の力学的エネルギーを式で書けば、

力学的エネルギー＝位置エネルギー＋運動エネルギー

である。

そして、摩擦などによる損失を無視すれば、力学的エネルギーがつねに一定であるという法則のことを力学的エネルギー保存の法則と呼ぶ。

遊園地にあるジェットコースターは、力学的エネルギーにおける、位置エネルギーと運動エネルギーのうつりかわりを利用している。そのため、ジェットコースターは、高い位置にきたときはコースターの速度がゆっくりであり、低い位置にいるときほどコースターの速度が大きい。

なお、コースターが始めに高い場所にのぼる時には、モーターによって、その高さまで上げられる。

弾性エネルギーと位置エネルギー

バネなども、振り子のように、速度最大の状態と、速度0の状態とをくりかえし、交互に運動をしつづける。

バネなどのような、力を加えると伸びるが、手を離すなどして力をのぞくと元の長さに戻る性質を、弾性（だんせい）というのであった。

そして、バネのように弾性のある物体にたくわえられたエネルギーのことを弾性エネルギーという。

弾性エネルギーは、以上の説明で述べたように、位置エネルギーと似た性質がある。（※ 検定教科書によっては、弾性エネルギーを、バネの場合の位置エネルギーである、として見なす場合もある。）

エネルギーの移り変わり

エネルギーには、運動エネルギーや位置エネルギーのほかにも、さまざまな形態がある。

たとえば、光のエネルギーや、熱のエネルギーなど。

そして重要なこととして、ある種類のエネルギーは、別の種類のエネルギーに変換されることがある。

たとえば、太陽からの光のエネルギーにより、水が加熱され、水蒸気とり、上空で雲となれば、

それはつまり、光のエネルギーが、上空にある雲としての位置エネルギーに変換されたことになる。

さらに雲が雨をふらせば、その落下する水滴の一部はダムに蓄えられる。

そして、そのダムの水の落下する力学的エネルギーによって、発電用タービンをまわし、こんどは電気エネルギーに変換されてゆく・・・・。

自然現象にかぎらず、工業製品でも同様である。たとえば電気ストーブは、電気を熱にしている。いっぽう、火力発電では、火の熱を使って電気を発電する。このように、電気エネルギーと熱エネルギーも、相互に変換できる。

生命現象でもエネルギーは変換されてゆくのは同じで、植物などのエネルギーも、もとをたどれば、太陽光の光エネルギーである。動物や植物の生き物の体のなかでも、さまざまな化学反応が起きているわけであり、物質のもつ化学エネルギーを利用しているわけである。

このように、エネルギーは、変換されてゆくことがある。

熱エネルギー

熱も、蒸気機関車などを考えれば分かるように、エネルギーを持っている。熱のもっているエネルギーを熱エネルギーという。

しかし、高温の物体を放置しておくと、しぜんに、まわりの物に熱を伝えてしまい、その物体は温度が下がっていって、最終的には、その物体は、まわりの環境と同じ温度になる。

このように、熱エネルギーは、まわりに散らばっていきやすい。

このように、熱エネルギーは、運動エネルギーや位置エネルギーとは、ちがう性質があるので、熱エネルギーは、力学的エネルギーには含めない。

熱エネルギーの理科の実験では、耐熱フラスコに入れた水を沸かして蒸気にして、その蒸気の力で、小型の風車をまわしたり、あるいはピストンのシリンダーを動かす実験などがある。

(※ あぶないので、ひとりでは実験しないこと。学校などで実験するさいも、やけどをしないように注意のこと。)

なお、物がこすれる現象である摩擦（まさつ）によって、熱エネルギーが発生する。

摩擦が起こるには、前提として、その物体が運動する事が必要である。つまり、摩擦が起こるには、前提として、運動エネルギーが必要である。

そして、摩擦によって熱エネルギーが発生するということは、つまり、運動エネルギーが摩擦によって熱エネルギーへと変化した事になる。

※ 熱と熱エネルギーは、ちがう。（名前が似ていて、まぎらわしいこともあるためか、）高校以上の理科では、熱エネルギーのことを内部エネルギーと呼んで区別することもある。（※ 教育出版）

理科的には、「熱」とは、高温の物体から低温の物体へと熱エネルギーが伝わる現象のことである。

たとえば石油ストーブは、石油の内部にたくわえられている熱エネルギーを取り出す仕組みの装置である、と理科的には考えている。

光エネルギーと熱エネルギー

ある物体に、日光などの光が当たると、その物体が熱くなるように、光は、その光を受けた物体に熱エネルギーを与える。

ということは、光そのものも、エネルギーを持っていることになる。

光のエネルギーのことを光エネルギーという。

音エネルギー

物体が何かにぶつかったとき、音が出る。

これは、運動エネルギーが失われたぶん、音に変わったことになるから、つまり、音もエネルギーである。

音のエネルギーのことを「音エネルギー」などという。

音とは空気の振動であるので、つまり、物体の運動エネルギーが、空気の振動のエネルギーへと変わったことになる。

わたしたちの耳が音を感じる仕組みは、耳の中にある鼓膜（こまく）があるが、空気の振動が鼓膜につたわり、そして鼓膜が振動するから、である。

さて、音をテープレコーダーなどに録音するマイクの仕組みは、マイクの中に、空気の振動をうけて振動しやすいような部品が、集音（しゅうおん）をするための部品として取り付けられている。マイクの、その集音をするための部品が振動することによって、その部品の位置がわずかにズレるので、マイク内にある電気回路での電気の流れやすさが変わる。

この、マイク内の電気回路での電気の流れやすさが、空気の振動によって変わることを利用して、マイクは音を感じ取り、テープレコーダーなどに録音している。

また、スピーカーなど音を発生させる機械は、そのスピーカーなどの内部に電気で振動する部品が入っている。スピーカー内の部品を振動させることで、空気を振動させ、音を発生させている、という仕組みである。

電気エネルギー

電気モータや、電気で動くオモチャのクルマなどを考えれば分かるように、電気によって運動エネルギーを発生させる事ができる。

また、静電気によって、髪が逆立つ（さかだつ）などの現象から分かるように、電気によって位置エネルギーを発生させる事ができる。

つまり、電気そのものも、エネルギーを持っている。電気のエネルギーのことを電気エネルギーという。

白熱電球（はくねつでんきゅう）や蛍光灯（けいこうとう）などの照明（しょうめい）の家電（かでん）などのよう、電気を流すことによって、光が出ることもある。

つまり、電気エネルギーによって、光を発生させられる。

また、磁石をもちいた、理科実験でもよくある発電の方法では、磁石を運動させる必要があるので、つまり、この発電方式では、運動エネルギーが必要である。

火力発電では、蒸気をわかして、その蒸気の力でタービンを回し、タービンに取り付けられた磁石のような物質を運動させている。つまり、火力発電は、熱エネルギーをもとにして、電気エネルギーを発電している。

さて、太陽電池を考えればわかるように、光エネルギーをもとに、電気エネルギーを取り出すこともできる。

化学エネルギー

化学反応によって、ある物質が高温になったり、逆に低温になったりする。つまり、化学反応によって、その物質の熱エネルギーの量が変わったことになる。

また、化学反応の結果、光が出る場合もある。

わたしたち生き物の食事も、胃や腸などでの消化（しょうか）や栄養の吸収などによって、食品を体内で化学反応させて、食品のもつエネルギーの一部をもとに、熱エネルギーをつくり出している。そのため、生き物は、体温を持っている。

エネルギー変換の効率

白熱電球(はくねつでんきゅう)をつけるとき、その電球に与えられた電力の多くは熱に消費されてしまう。

つまり、白熱電球をもちいて、電気エネルギーを光エネルギーに変換したいという目的なのに、目的外の熱エネルギーに多くのエネルギーが使われてしまう。

このように、機械や工業製品などをもちいてエネルギーを変換するとき、いくらかの割合が目的外の種類のエネルギーに変換されて消費されてしまう。

白熱電球では、電球に与えた電気エネルギーの90%以上は熱エネルギーとして消費されてしまう。残りの約10％だけで、電球は光を出しているのである。

いっぽう、蛍光灯では、同じ明るさにしたいとき、白熱電球より電力を小さくできる。

さらに、LED電球では、同じ明るさにしたいとき、蛍光灯よりも消費電力を小さくできる。

このようにLEDや蛍光灯は、白熱電球よりも変換効率が高い。

また、LED電球は、同じ明るさの白熱電球や蛍光灯と比べて、あまり熱くならない。（※ かといって、さわってヤケドをしないように。興味があって実験したいなら、放射温度計や赤外温度計などで調べると安全だろう（推測）。直接はLEDにさわらず、LEDの明かりをオフにしてから、放射温度計などで調べるといいかもしれない。）

このLEDの温度上昇の少なさから、確かにLEDでは、光に変換される効率が高いことが分かる。

投入されたエネルギーの対して、利用できるエネルギーの割合を、効率（こうりつ）という。

白熱電球はエネルギー変換の効率が悪いことから、日本では近年、白熱電球が廃止されていき、LED電球などへの切り替えが進んでいる。

熱とエネルギー

エネルギーを使った機械には、力学的エネルギーを使った機械のほか、電気エネルギーを使った機械や、化学エネルギーを使った機械などいろいろな機械があるが、どんな機械であっても、熱エネルギーが利用しないのに発生してしまう。

また、熱に加えて、さらに音などの振動エネルギーとして、エネルギーが利用されずに放出される場合もある。（※ 東京書籍の教科書）

※ 熱の伝わりかたなどについては『中学校理科第1分野/熱と温度』で説明した。

発展: 落下運動

（※ 検定教科書で、落下運動の記述を確認）

物体を地面から離して速度は付けずに落下させた場合、手を離した直後の初速度は秒速0m/sだが、障害物などがなければ、1秒後は約9.81m/sの速度になっており、2秒後は約19.6m/sの速度になっており、3秒後は約29.4m/sになっており、・・・というふうに1秒ごとに約9.81m/sずつ速度が増していく。地面に当たるまで、このような加速を続けていく。

このような、障害物などが無く、落下を続けていく落下運動を自由落下（じゆうらっか、free fall）という。

また、速度の変化率のことを加速度(かそくど)（英語: acceleration、アクセラレーション）という。自由落下する物体は、重力によって、鉛直方向の下向き（つまり地面に向かう向き）に、一定の加速度 g （=約9.81m/s²）で加速するので、この重力による加速度を重力加速度（じゅうりょくかそくど）という。重力加速度の記号は、一般に小文字の g で表す。地球上での重力加速度 g の大きさは、約9.81m/s²である。これは地上での重力による加速度なので、月面では1/6倍になることに注意せよ。

また、無重力下では重力加速度はゼロ（ 0 m/s²）になる。

加速度の単位はm/s²であり、速度の単位のm/sとは異なることに注意せよ。

加速度の単位の意味は、一秒あたり（= 1/s ）の速度 m/s の変化率なので、

一秒あたり変化率 1/s × 速度 m/s = 加速度 m/s²

となる。

また、加速度が一定の運動を、等加速度運動(とうかそくどうんどう)という。自由落下は等加速度運動の一つの例である。

自由落下の重力加速度は、どの物体に対しても共通である。

空気抵抗

羽毛や紙などの軽い物を落下させた時にゆっくり落ちる現象があるが、この現象は、空気による抵抗である。実際に、実験で、真空にした透明容器内などで羽毛や紙などの落下をさせると、金属などと同じ落下速度で落ちることが、実験的にも確認されている。

空気による運動への抵抗を空気抵抗（くうきていこう、air resistance）という。

パラシュートなどを考えればわかると思うが、質量に対して幅が大きい物は、空気抵抗を受けやすい。紙や羽毛などが空気抵抗を受けやすいのも、パラシュートなどと同様の仕組みである。

（なお、真空を作る実験は、真空ポンプなどを用いることになるが、ポンプの使用法に関する専門的な知識が必要なので、中学生には実験が難しいので、行わないほうがいいかもしれない。もし真空での落下実験に興味があれば、映像教材などを学校の先生に見せてもらうか等をしてください。）

放物線

放物線
３通りの初速度で、斜め上方向に角度を同じにして投げた場合。
縦軸が鉛直方向。横軸が水平方向。

ボールなどを斜め上向きに投げたら、どういった軌跡を描くだろうか。空気抵抗は考えないとする。投げたボールにも重力は働くので、上向きの速度が少しずつ減速していく。しかし横向きの速度成分は重力の方向とは別方向なので、横向き成分は変化をしない。結果的に投げたボールは鉛直下向きに加速していくので、右図のような軌跡を描く。このような、物体を投げた時の軌跡を、放物線（ほうぶつせん、parabola、パラボラ）という。

発展: 運動方程式

（※ 検定教科書で、運動方程式の記述を確認）