中学校理科 第1分野/熱と温度

発展	この項目では発展的な内容を取りあつかっています。 このページのほうは読み飛ばしてもかまいません。

熱と温度

摂氏温度

セルシウス温度計

さて、「温かい、暖かい、暑い、熱い」とか「寒い、冷たい、冷える」とかを定量化したものを、温度(おんど)と呼ぶことにしよう。 温度の単位として実用上、多く用いられている℃単位の摂氏温度(せっしおんど)を用いる。摂氏温度は、セルシウス温度（Celsius temperature）とも言う。また、温度差をセルシウス度（degree Celsius）といい、これはケルビン（kelvin；単位記号 K）に等しい。

摂氏温度（セルシウス温度）

定義

熱力学的温度の値をケルビン（K）で表し、273.15を引いた値。

$t{[^{\circ }{\text{C}}]}=T{[{\text{K}}]}-273.15$

由来

1気圧の水の沸点を100℃、凝固点を0℃とし、その間を100等分したものを1度(degreeあるいはdeg)とした。

摂氏度（セルシウス度）

ケルビンに等しい

ケルビン

ボルツマン定数を 1.380649×10⁻²³ J/K とすることによって定まる温度。

温度計の種類にアルコール温度計や水銀温度計などあるが、これらは物体の温度が上がることによる膨張を、温度の測定器として利用した器具である。

また、アメリカ合衆国含む一部の国では、ヤード・ポンド法の華氏温度(かしおんど)が使われている。日本の計量法などの法令でカ氏度は、「例外的に限定した取引又は証明」に用いる場合以外は認められておらず、日常的に華氏を使う機会は少ない。また、SIでは華氏温度も摂氏温度と同様にケルビンから導出されている。

熱量

「熱量(ねつりょう)とは何か」を述べる前に、たとえ話をする。 1kgの物体と、べつの1kgの物体を合わせて、重量計に載せれば、測定値は2kgになる。 だが、容器に入った10℃の水に、等量の10℃の水を注いでも、20℃にはならない。

いっぽう、温度を上げるには、エネルギーが必要だが、エネルギーは足しあわせができる。 このような理由から、加熱された物体に蓄えられた熱エネルギーと温度とを区別する必要がある。 そこで、熱エネルギーのことを熱量(ねつりょう)（英語: heating value）といい、これは温度とは区別する。

熱量の単位はカロリー(フランス語: calorie)といい、単位の記号はcalと書く。1cal は、水 1g の温度を 1℃ 上昇させるのに必要な熱エネルギーのことである。ここでいう「水」とは、5℃の冷水だろうが、80℃の熱湯だろうが、凝固や沸騰していない液体のH₂Oのことであるとする。

ともかく水の熱量の式は、

熱量(カロリー) = 水の質量（グラム単位g） × 温度差（℃単位）

である。 栄養学の分野ではキロカロリー（kcal しばしば、Cal と綴られカロリーと発音されることに注意）が用いられることが多い。中学でも、熱量の計算にはカロリーを用いても良いだろう。

水以外の物質は、同じ熱量を与えても、水とは温度の変化しやすさが違う。 たとえば、夏場で、鉄が熱くなってるのを体験した人もいるだろう。この理由の一つは、鉄と水とでは、温度の変化のしやすさが違うからである。

まず、1cal とは、水 1g の温度を 1℃ 上昇させるのに必要な熱エネルギーのことである。

1gの物質を、温度を1℃上昇させるのに必要な熱量を比熱(ひねつ)という。比熱の単位は　ジュール毎キログラム温度 　J/(g・℃)

水そのものの比熱は1とする。

物質の熱量の式は、

熱量(カロリー) = 比熱　×　質量（グラム単位g） × 温度差（℃単位）

である。

温度と分子運動

ブラウン運動の概念図（シミュレーション）。黒色の媒質粒子の衝突により、黄色の微粒子が不規則に運動している。

物体の温度の正体とは、実はその物体を構成している、それぞれの分子の運動の激しさのことである。この温度による運動は、その物体の、いくつもの分子が、ぶつかりあってるので、不規則である。

このように、物質をつくっている分子が衝突しあっていることを分子運動(ぶんし うんどう)という。

分子運動の強さが分子どうしの引力に比較して無視できるほどまでに弱ければ、抑えこまれてしまい物体が固体状の形状を保つ。これが温度が低いと固体になる理由である。

固体でも、分子は、結晶の格子点を中心に運動している。液体では、外部から力を加えると、体積は変わらないものの、流動して容易に形を変える事ができる。

固体を加熱するなどして温度を高めると、いずれ、固体から液体へ変わる。これは、熱運動が強まり、もはや結晶の構造を取るのが不可能になったからである。

液体を加熱していくと、いずれ、気体へ変わる。気体は分子運動が、分子間力よりもはるかに大きく、もはや、各分子がバラバラに離れて行動している状態である。したがって、液体から固体になると体積が増える。

なお、液体から気体への変化にかぎらず、一般に物体は温度が上がると、ほとんどの物質で体積が増える。

熱の伝わり方

熱は、外部から手を加えなければ、自然と温度の高い所から、温度の低いところへと移動していく。 その結果、温度の高かった場所は、熱を手放していき、だんだんと温度は低くなる。逆に、周囲と比べて温度の低かった場所は、しだいに温度が高くなる。そして、いつしか、ふたつの箇所の温度は同じになる。このような熱の移動が無い状態を熱平衡(ねつへいこう)という。 いっぽう、熱が、温度の低いところから、温度の高い所へと自然に移動することは、無い。

さて、静止した物体での熱の伝わり方には、大きく分ければ、熱伝導(ねつでんどう)（英語: thermal conduction、サーマル・コンダクション）と対流(たいりゅう)（英語: convection、コンベクション）と熱放射(ねつほうしゃ)（英語: radiation、ラディエイション）の三つに分けられる。

対流

上と下とで温度差のある場所での、対流の一例。下から入力された熱は、対流によって上部へと運ばれ、流体表面からの熱放出によって冷やされた後は下部へと潜る。

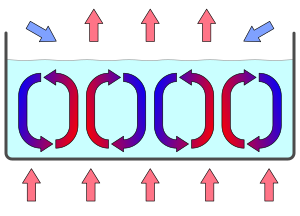
熱を持った物体そのものが静止していても、となりにある気体や液体などが運動すれば、その気体などが熱を運ぶ。これを対流（convection、コンベクション）という。 気体や液体などでは、温度差があると、温度が高いほど密度が軽く浮力が生じるので、自然に対流が起こりやすい。

密度変化による対流の場合は、循環運動をする場合が多い。なぜなら、暖められて密度が軽くなることで浮力が発生し、そのため暖められた物体が上方に移動し、かわりに元から上部にあった冷たい物体が押しのけられ、押しのけられた冷たい物体は重力によって降りてくる。

熱伝導

対流が起きなくても、固体などの物質どうしが接触していけば、熱は伝わっていく。これを熱伝導（thermal conduction、サーマル・コンダクション）という。

金属は、熱伝導をしやすい。なので、台所のフライパンなどの加熱するための調理器具は、金属製なのである。

分子運動の伝搬が、熱伝導の起きる理由である。

熱放射

可視光の熱放射が、このような熱された金具で見ることができる。赤外線領域での放射は、人間の目と画像で撮影されたカメラには見えないが、赤外線カメラでは撮影できる。

実は、どの物体も、人間の目には見えないが、電磁波という電場と磁場の変化を伝搬する波を出している。電磁波を出すことを放射（radiation、ラディエイション）という。その放射する電磁波が、人間の眼に見えないのは、単に放射電磁波の周波数が、人間の目の可視領域で無いからという理由である。

この放射する電磁波は、常温では周波数が低く、赤外線の領域である。高温になるほど、物体の放射電磁波の周波数が高くなり、可視領域へと入っていく。溶鉱炉などで、高温で溶けた金属が光るのは、この放射光によるものである。このような高温物体から電磁波がでることを熱放射(ねつほうしゃ)、あるいは単に放射という。熱輻射(ねつふくしゃ)と言う場合もある。 この放射電磁波によっても、エネルギーが高温側の物体から低温側の物体に輸送される。低温側からも放射電磁波が出るが、高温側の物体のほうが放射電磁波のエネルギーが大きいので、差し引きして、結局は、高温側から低温側へとエネルギーが移る。

発展的な説明

発展 ボイルの法則

ボイルの法則
縦軸が圧力。横軸が体積。値はロバート・ボイル本人のオリジナルデータ。

ロバート・ボイル（Sir Robert Boyle）という人物が、容器内の気体の温度を変えずに、一定温度での気体の圧力と気体の体積との関係を調べたところ、法則性を発見した。

外部から、ピストンを押しこむなどして、気体の体積を半分にすると、気体の圧力が2倍になる。 （ピストン内の気体の圧力を測るには、たとえばピストンの可動部に外側から重りを載せるなり、あるいはバネばかりを利用するなりと、ともかく工夫すれば可能である。）

同様に、気体の体積を${\frac {1}{3}}$倍にすると、圧力が3倍になる。同様に、気体の体積を${\frac {1}{4}}$倍にすると、圧力が4倍になる。 以下、気体体積の${\frac {1}{5}}$倍や${\frac {1}{6}}$倍でも同様である。べつに気体体積は整数倍でなくても、たとえば

${\frac {1}{3.942}}$倍とか、どんな数字でも、同様の法則が成り立つ。

これ等をまとめると、気体の圧力p[Pa]と体積V[m³]との関係には、以下の関係式がある。

pV=K

（Kは定数）

この関係式を、ボイルの法則（ボイルのほうそく、Boyle's law）という。

シャルルの法則

シャルルの法則の概念図
縦軸は体積で、このグラフではミリリットル単位。横軸の温度はこのグラフでは℃単位。

さて、シャルルという人物が、温度と容積の関係を測って研究したところ、法則性を発見した。大気圧の状況下では、気体を1℃温、上昇させると、0℃の体積の${\frac {1}{273}}$ずつ膨張することを、シャルルは発見した。

これを式で表すと、0℃のときの気体の体積をV0として、一般の温度の体積をVとすると、温度t[℃]のときの関係式は、

$V=V_{0}(1+{\frac {t}{273}})$

であることを、シャルルは発見した。 この法則をシャルルの法則（英: Charles's law）という。

絶対零度

シャルルの観測結果をグラフに書くと、マイナス273.15℃で、理論上では気体は体積が0になる。このマイナス273.15℃を絶対零度(ぜったいれいど)（英語: absolute zero、アブソリュート・ゼロ）という。絶対零度以下の温度は、測定誤差の範囲程度を除けば、理論上は考えらない。 また実験的にも絶対零度以下の温度は、測定誤差の範囲程度を除けば、確認されていない。たとえばマイナス300℃やマイナス500℃などは実在しない。

なお、現代では、絶対温度に273.15を足した値がセルシウス温度と定義されている。

「w:ケルビン#新定義」も参照

絶対零度のマイナス273.15℃とは、分子運動の全くない状態である（ただし量子力学では、不確定性原理のため、原子の振動が止まることはない）。