高校物理熱力学

気体

ボイルの法則

（参考画像）

シリンダーの中に入れられた気体を、温度を一定に保ちながらピストンを押して圧力をn倍にすると、気体の体積は ${\frac {1}{n}}$ 倍になる。このことから、温度一定のとき、気体の圧力 $p$ と体積 $V$ は反比例する：

pV=k

(k:定数)

また、変化前の気体の圧力と体積を $p_{1}$ , $V_{1}$ 、変化後の圧力と体積を $p_{2}$ , $V_{2}$ とすると、

p_{1}V_{1}=p_{2}V_{2}

と表現できる。

シャルルの法則

（参考画像）

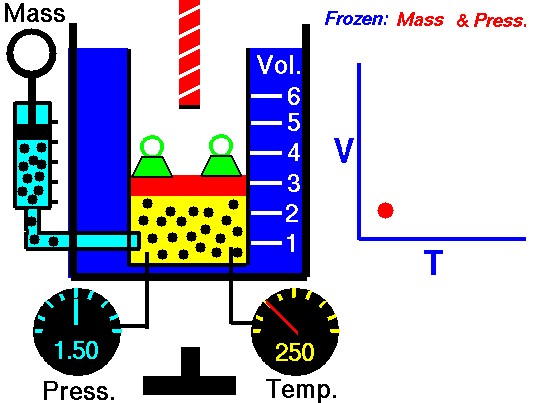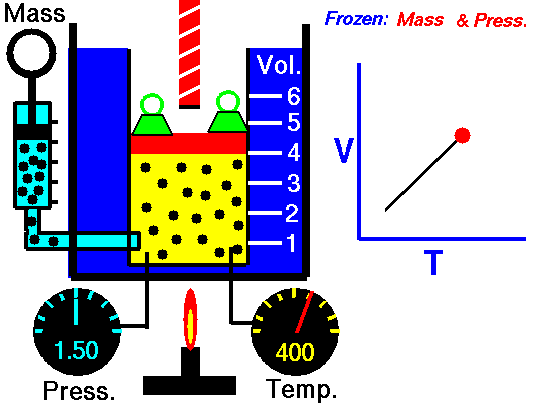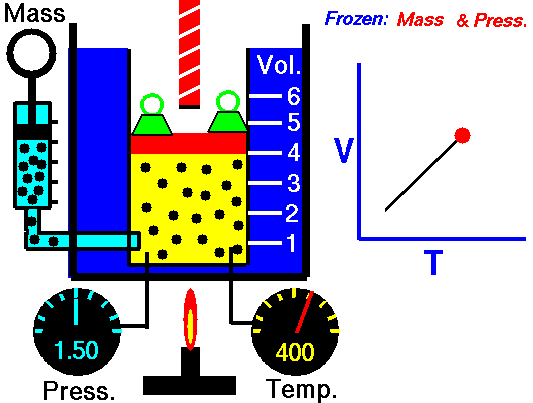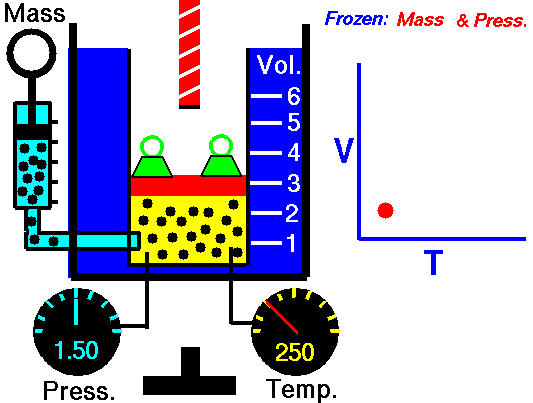
気体を圧力を一定に保ちながら気体の温度を変化させると、気体の体積 $V$ と絶対温度 $T$ は比例する：

{\frac {V}{T}}=k

(k:定数)

また、変化前の気体の圧力と絶対温度を $V_{1}$ , $T_{1}$ 、変化後の圧力と体積を $V_{2}$ , $T_{2}$ とすると、

{\frac {V_{1}}{T_{1}}}={\frac {V_{2}}{T_{2}}}

と表現できる。

ボイル・シャルルの法則

ボイルの法則から、気体の体積 $V$ と圧力 $p$ は反比例し、シャルルの法則から、気体の体積 $V$ と絶対温度 $T$ は比例する。これらより、気体の体積 $V$ は絶対温度 $T$ に比例し圧力 $p$ に反比例する：

V=k{\frac {T}{p}}

より

{\frac {pV}{T}}=k

(k:定数)

理想気体

ボイル・シャルルの法則から、圧力を上げたり、温度を下げていくと気体の体積は 0 に近づくはずである。しかし、現実には気体分子の体積や、分子間力が存在するため、ボイル・シャルルの法則からは外れることになる。ボイル・シャルルの法則が厳密に成り立つ仮想的な気体を理想気体といい、現実に存在する気体を実在気体という。理想気体では、気体分子の体積と分子間力が無視できる。

高音低圧では、実在気体は理想気体として近似できることが知られている。また、分子間力の影響が小さい、分子量が小さくて無極性分子である気体も理想気体として近似できる。

理想気体の状態方程式

1 mol の理想気体について、ボイル・シャルルの法則の定数 $R={\frac {pV}{T}}$ の値は、 $R=8.31\,\mathrm {J/(mol\cdot K)} =8.31\times 10^{3}\,\mathrm {Pa\cdot L/(mol\cdot K)}$ ^[1]であり、 $R$ を気体定数という。

理想気体の物質量が $n$ の場合、気体の体積は物質量に比例するため、 $R={\frac {p}{T}}{\frac {V}{n}}$ より $pV=nRT$ を得る。これを理想気体の状態方程式という。

実在気体の状態方程式

$Z={\frac {pV}{nRT}}$ を圧縮因子という。理想気体においては常にZ=1である。

圧縮因子の値が1からかけ離れているほど、その気体は理想気体からかけ離れている。0≦Z<1ならば分子間力、z＜1ならば分子自体の体積の影響が大きい。

理想気体の状態方程式に補正を加えて実在気体の実際の振る舞いに近づける方法はいくつかあるが、ここでは以下のような方法を紹介する。

実在気体の圧力を $p_{r}$ 、体積を $V_{r}$ とする。

分子間力が働くと、分子が器壁に衝突する際に近くの分子に引き寄せられて圧力が低くなる。下記の気体分子運動論の結果から考察して、衝突の勢いの減少量・衝突頻度ともに ${\frac {n}{V}}$ となるので、気体の分子間力によって壁が受ける圧力の減少量は ${\frac {n^{2}}{V_{r}^{2}}}$ に比例する。比例定数をaとおくと、分子間力を考慮して補正した圧力は、 $p_{r}+a{\frac {n^{2}}{V_{r}^{2}}}$ である。

気体の体積とは、気体分子が自由に動くことのできる三次元領域の体積のことである。分子自身の体積によりこの体積の値は減少する。このとき、減少した体積を排除体積という。1molあたりの排除体積をbとすると、分子自身の体積を考慮して補正した体積は、 $V_{r}-nb$ となる。

これらを理想気体の状態方程式に代入すると、 $(p_{r}+a{\frac {n^{2}}{V_{r}^{2}}})(V_{r}-nb)=nRT$ となる。この状態方程式を、ファンデルワールスの状態方程式という。この方程式に従う気体をファンデルワールス気体という。また、定数a, bをファンデルワールス定数という。ファンデルワールス定数は気体の種類にのみ依存する。

ファンデルワールスの状態方程式は、補正が簡単かつ応用範囲が広い。しかし、低温領域において、ファンデルワールス気体の振る舞いは理想気体とも実在気体ともずれてしまう。振る舞いがよく近似できる最低温度を臨界温度という。

現在では、更に修正された形の状態方程式が提案されている。

気体分子運動論

気体の圧力という巨視的な状態について、気体分子の運動といった微視的な視点から考察してみよう。

容器に衝突した分子の運動量変化

圧力の仕組みを分子1個1個から考える。気体分子は質点とする。

一辺の長さLの立方体の容器に、気体が入っているとしよう。分子1個の質量を $m$ とする。これが速度 $v$ で運動していたとして、速度 $v$ の $x$ 成分を $v_{x}$ とする。

容器の中で運動している分子が、 $x$ 軸に垂直な右側の壁にあたったとする。壁は、静止していて、弾性衝突であるとする。よって、衝突の前後で、分子の速度の大きさは変わらない。

分子の運動量の変化は、図より、以下のようになる。

m(-v_{x})-mv_{x}=2mv_{x}

これは、容器の側から見れば、同じ大きさの力積を気体分子1個から受けとることになる。つまり、 $x$ 軸に垂直な容器の壁が、気体分子1個の1回の衝突で受けた力積は $2mv_{x}$ である。

時間 $t$ の間に、この分子が壁に衝突する回数は ${\frac {v_{x}t}{2L}}$ である。なぜならば、往復に2Lの距離を移動して、速度は $v_{x}$ だからである。（壁は右側と左側の両方にあるが、左側の壁が受ける力積は右側の壁の力積にはならないので、片方の壁だけが受ける衝突だけの力積を計算する必要がある。）

衝突回数 ${\frac {v_{x}t}{2L}}$ と、1回の衝突の力積 $2mv_{x}$ を掛け、時間 t で割れば、単位時間あたりに壁が受ける力積が出てくる。

2mv_{x}\cdot {\frac {v_{x}t}{2L}}\cdot {\frac {1}{t}}={\frac {mv_{x}{}^{2}}{L}}

単位時間あたりの力積とは、 $F\Delta t$ の $\Delta t$ が1なので、力そのものである。つまり、これが気体分子1個が壁に及ぼす力である。

次に気体分子全体が壁に与える力を求めたい。まず速度 $v_{x}$ は分子ごとに異なるので、分子速度の平均で考える必要がある。 $v_{x}^{2}$ の平均を ${\bar {v_{x}^{2}}}$ で表そう。

分子の数を $N$ 個とすれば、気体分子全体が右側の壁に与える力Fは、

F={\frac {Nm{\bar {v_{x}{}^{2}}}}{L}}

これを壁の面積 S=L²で割れば、右側の壁に与える圧力 Pが求まる。

P={\frac {Nm{\bar {v_{x}{}^{2}}}}{L^{3}}}

ここで、 $L^{3}$ は、容器の体積である。

したがって、圧力Pは、

P={\frac {Nm{\bar {v_{x}{}^{2}}}}{V}}

と書ける。

速度のx方向成分 $v_{x}$ と、速度 $v$ の関係を求める。

N個の分子の $v,v_{y},v_{z}$ の2乗の平均を ${\bar {v^{2}}},{\bar {v_{y}^{2}}},{\bar {v_{z}^{2}}}$ とすると、三平方の定理より、

{\bar {v^{2}}}={\bar {v_{x}{}^{2}}}+{\bar {v_{y}{}^{2}}}+{\bar {v_{z}{}^{2}}}

である。

ここで ${\sqrt {\bar {v^{2}}}}$ を2乗平均速度（root mean square velosity）という。二乗平均速度は速度の絶対値の平均と多少値が違う。平均に関してはw:平均に詳しい解説があるので、適宜参照されたし。ただし高校段階ではこの平均の問題に深入りする必要は全くない。

また、気体の速度に特別な方向は無いと考えられるので^[2]、

{\bar {v_{x}{}^{2}}}={\bar {v_{y}{}^{2}}}={\bar {v_{z}{}^{2}}}

である。よって、

{\bar {v_{x}{}^{2}}}={\frac {\bar {v^{2}}}{3}}

である。

これを圧力の式に代入すれば、

P={\frac {Nm{\bar {v{}^{2}}}}{3V}}

となる。

気体分子の運動エネルギー

p={\frac {Nm{\bar {v{}^{2}}}}{3V}}

から

pV={\frac {Nm{\bar {v{}^{2}}}}{3}}

を得る。気体のモル数

n

と分子数はアボガドロ定数

N_{\mathrm {A} }

の関係

N=nN_{\mathrm {A} }

を代入し、理想気体の状態方程式

pV=nRT

と比較すれば、

nRT={\frac {nN_{\mathrm {A} }m{\bar {v{}^{2}}}}{3}}

{\frac {1}{2}}m{\bar {v^{2}}}={\frac {3}{2}}\left({\frac {R}{N_{\mathrm {A} }}}\right)T

を得る。ここで、ボルツマン定数 $k_{\mathrm {B} }={\frac {R}{N_{\mathrm {A} }}}$ を定義^[3]すると、

{\frac {1}{2}}m{\bar {v^{2}}}={\frac {3}{2}}k_{\mathrm {B} }T

を得る。

これが、気体分子1個の運動エネルギーの平均値である。

気体分子の速度

気体分子1個の運動エネルギーの平均値の式 ${\frac {1}{2}}m{\bar {v^{2}}}={\frac {3}{2}}k_{\mathrm {B} }T$ を ${\sqrt {\bar {v{}^{2}}}}$ について解けば、2乗平均速度 ${\sqrt {\bar {v{}^{2}}}}$ が求まる。

{\sqrt {\bar {v{}^{2}}}}={\sqrt {\frac {3k_{\mathrm {B} }T}{m}}}={\sqrt {\frac {3RT}{mN_{\mathrm {A} }}}}={\sqrt {\frac {3RT\times 10^{3}}{M}}}

ここで、分子量 $M$ は $M=mN_{\mathrm {A} }\times 10^{3}$ ^[4]を満たすことを使った。

この式から 0 °C(273.15 K) における酸素分子の速さの平均を求めてみると 461 m/s であり、0℃における音速の 332 m/s よりも速く運動していることが分かる。

内部エネルギー

気体の内部エネルギーは分子の熱運動による運動エネルギーと分子間力による位置エネルギーの和である。

ここで、分子間力による位置エネルギーは無視できるほど小さいので、内部エネルギーは熱運動による運動エネルギーに等しいとする。

単原子分子の場合は、分子の回転を無視できるため、内部エネルギーは、運動エネルギーのみからなると見なしてよい。

単原子分子理想気体の内部エネルギー $U$ は

U={\frac {3}{2}}NkT={\frac {3}{2}}nRT

である。

熱力学

気体のする仕事

シリンダー内に気体を入れ、なめらかに動く表面積 $S$ のピストンで閉じ込める。ピストンの外の大気圧が $p$ のとき、シリンダー内の圧力も $p$ である^[5]。シリンダー内の気体に熱を与え、気体をゆっくり膨張させる。ピストンが $\Delta l$ 動いたときまで、気体がピストンに加える力は $pS$ である。気体がピストンにした仕事 $W'$ は $W'=pS\Delta l=p\Delta V$ である。

p-Vグラフ

気体の圧力が変化する場合でも、p-Vグラフで囲まれた面積から気体が外部にする仕事を求められる。

積分を使って表すと、 $W'=\int _{v_{1}}^{v_{2}}p(v)\,dv$ である。

定積変化と定圧変化と等温変化と断熱変化

定積変化では、気体の体積は一定なので、気体が外部にする仕事は $W'=p\Delta V=0$ である。従って熱力学第一法則より、 $\Delta U=Q$ である。

定圧変化では、気体が外部にする仕事は $W'=p\Delta V$ なので、気体がされた仕事は $W=-W'=-p\Delta V$ 。熱力学第一法則より、 $\Delta U=Q-p\Delta V$ である。

等温変化では、気体の内部エネルギーの変化は0である。熱力学第一法則より $0=\Delta U=Q+W$ である。

断熱変化では、外部との熱の出入りがないので、 $Q=0$ である。熱力学第一法則より $\Delta U=W$ である。

(熱伝導の大きいシリンダーで)ピストンをゆっくと動かすと、シリンダー内の気体の温度を外気温と同じに保つことができるため、等温変化が実現できる。

熱伝導の小さいシリンダーを使ったり、ピストンを極めてすばやく動かすと外部と気体の熱の出入りが無視できるため、断熱変化が実現できる。

モル比熱

気体1molに対して、温度を1K上げるのに必要な熱量をモル比熱（molar heat capacity）という。

n

の気体に熱量

Q

を与えて温度

\Delta T

だけ上がったとすれば、モル比熱

C

は

C={\frac {Q}{n\Delta T}}

である。

さて、気体の温度を上げると、状態方程式から分かるように圧力や体積が変わる。もし、気体を変形が可能な容器（たとえばピストンヘッドが動けるシリンダー内部）に入れれば、温度を上昇させる際に気体は膨張し容積が上昇するので、外部に仕事をすることになる。

いっぽうで、もし、容器が固くて変形しない場合で、加熱によって温度や圧力のみが変わる定積変化の場合は、気体は外部に仕事をしない。

これらを考えると、容器の条件によって、比熱が変わるので、条件ごとに区別をする必要がある。

定積モル比熱

定積変化の場合のモル比熱を定積モル比熱（molar heat at constant volume）という。

定積モル比熱 $C_{V}$ は定義より、 $C_{V}={\frac {Q}{n\Delta T}}$ である。

定積変化では体積一定なので熱力学第一法則より

\Delta U=Q\quad \therefore \Delta U=nC_{V}\Delta T=Q

.

もし気体が単原子分子理想気体ならば、内部エネルギーの変化量は

\Delta U={\frac {3}{2}}nR\Delta T

であったので

{\frac {3}{2}}nR\Delta T=nC_{V}\Delta T

より

C_{V}={\frac {3}{2}}R

　（単原子分子理想気体）

である。

定圧モル比熱

定圧変化の場合のモル比熱を定圧モル比熱（molar heat at constant pressure）という。

単分子原子理想気体の定圧モル比熱を求めてみよう。圧力 $p$ で物質量 $n$ の単分子原子理想気体の温度が $\Delta T$ 上がったときの内部エネルギーの変化量 $\Delta U$ は

\Delta U=Q-p\Delta V

である。理想気体の状態方程式より、定圧変化では圧力一定のなので、

p\Delta V=nR\Delta T

である。

また、単分子原子気体の内部エネルギーの変化は

\Delta U={\frac {3}{2}}nR\Delta T

である。これを代入して

Q=\Delta U+p\Delta V={\frac {5}{2}}nR\Delta T

を得る。定圧モル比熱は $Q=nC_{p}\Delta T$ が成り立つので

これより、 $C_{p}={\frac {5}{2}}R$ である。

同様にして、二原子分子理想気体においては $C_{V}={\frac {5}{2}}R,C_{p}={\frac {7}{2}}R$ であることが証明できる。

熱力学第一法則の式 $\Delta U=Q-W$ に $Q=nC_{V}\Delta T,W=p\Delta V=nr\Delta T,\Delta U=nC_{V}\Delta T$ を代入すると、 $C_{V}=C_{p}-R$ すなわち $C_{p}-C_{V}=R$ を得る。これをマイヤーの関係式という。

定圧モル比熱と定積モル比熱の比 $\gamma ={\frac {C_{p}}{C_{V}}}$ を比熱比という。

理想気体が（P, V, T）の状態から（P+ΔP, V+ΔV, T+ΔT）の状態に移ったとする。それぞれの状態について、理想気体の状態方程式より ${\begin{cases}PV=nRT\\(P+\Delta P)(V+\Delta V)=nR(T+\Delta T)\end{cases}}$ である。変形すると $P\Delta V+V\Delta P+\Delta P\Delta V=nR\Delta T$ である。ここで、微小量同士の積を無視することにすると、 $P\Delta V+V\Delta P=nR\Delta T$ を得る。

熱力学第一法則 $\Delta U=Q-W$ において、 $\Delta U=nC_{V}\Delta T$ 、 $W=P\Delta V$ 、断熱変化のとき $Q=0$ より、 $nC_{V}\Delta T=-P\Delta V$ である。先ほど得た式を用いてΔTを消去すると、 $C_{V}V\Delta P=-(C_{V}+R)P\Delta V$ である。整理して ${\frac {\Delta P}{P}}=-{\frac {C_{V}+R}{C_{V}}}{\frac {\Delta V}{V}}$ を得る。ここで、マイヤーの法則より $C_{V}+R=C_{p}$ 、比熱比の定義より $\gamma ={\frac {C_{p}}{C_{V}}}$ なので、 ${\frac {\Delta P}{P}}=-\gamma {\frac {\Delta V}{V}}$ である。

両辺それぞれ積分すると、 $\int {\frac {dP}{P}}=-\gamma \int {\frac {dV}{V}}$ より積分定数をAとして $\log P=-\gamma \log V+A$ である。変形して $\log P+\log V^{\gamma }=\log PV^{\gamma }=A$ すなわち $PV^{\gamma }=e^{A}=const.$ である。

この、 $PV^{\gamma }=const.$ という関係をポアソンの法則という。

熱機関

熱機関とサイクル

熱をもらって仕事をする装置のことを熱機関という。

自動車のガソリンエンジンや飛行機のジェットエンジンは、熱機関である。

なお、発電所の蒸気タービンも、熱機関とみなすのが一般的である。

熱機関は、たとえばピストン部分があって、ピストンが膨張して、また元の体積に戻ったりするなど、周期的に状態を繰り返すので、熱機関の動作の過程をサイクルという。

熱機関は、周囲の高温部分から熱をもらうだけでなく、周囲の低温部分に熱をすてなければならない。

なお、熱機関は、けっして、低温部分から熱をもらって、高温部分に熱をすてる事はない（もしあったとしたら、高温部分はますます高温になってしまうし、低温部分はますます低温になってしまう）。

仕事をする熱機関は、かならず高温部から熱をもらって仕事をして、低温部分に熱をすてるので、よって熱は自然には高温部から低温部に移動する。

例外としてクーラーやエアコンのように外部から電力などのエネルギーを加えないかぎり、けっして自然には、低温部から高温部に自然に移動させる事はない。

外部からエネルギーの加わってない熱機関では、自然には高温部から低温部に熱を移動させる事はあっても、けっして、低温部から高温部に自然に移動させる事はなく、これを熱力学の第2法則という。

また、すべての熱を仕事に変換する事は不可能であり、これも熱力学の第2法則に含める。

もし、受け取った熱をすべて仕事に変換できる熱機関があるなら、低温部分から受け取った熱を自然に高温部分に渡してしまう事もできてしまうと考えられている。

また、上述のように、逆の場合のない現象のことを不可逆変化という。いっぽう、逆の現象もあり得る場合は可逆変化という。

熱機関の運動は、厳密には、普通は不可逆変化である。（ただし、ある熱機関の熱効率が高い場合に、近似的に可逆変化として計算する場合がある。）

たとえば、摩擦で止まる物体は、自然界には、けっして逆の現象はない。つまり、静止している物体が周囲から熱（摩擦熱の逆に相当）を受け取って、運動を始めるという現象は、自然界には存在しない。

つまり、このような考え方でいうなら、摩擦による物体の静止もまた、不可逆変化の一例である。

熱効率

気体を膨張させて仕事を取り出す熱機関（ねつきかん、thermal efficiency）が、あるとする。この熱機関の内部気体を圧縮させて戻すのにも、エネルギーが必要である。したがって、加熱膨張させて仕事をさせたあとは、熱機関の熱を放熱しないと、圧縮に膨張時と同じエネルギーが必要になり、熱機関として価値が無くなる。だから熱機関を繰り返し利用して仕事をさせるためには、加熱をして膨張をしたあとに、気体を収縮させる際に、冷却あるいは放熱して元の圧力や体積に戻すことになる。

低温熱源

したがって、熱機関には冷却源や放熱先が必要である。このような冷却源や放熱先を低温熱源という。（冷却をする場合は、当然に冷却源が必要である。放熱をさせる場合も、放熱先は温度が熱機関よりも低い必要があるから、結局、冷却源があることと同等になる。）「低温熱源」という呼び方に関して、熱を捨てる先なのに「熱源」というのは奇妙と感じるかもしれないが、便宜上、こういうので、慣れて頂きたい。

高温熱源

対して、膨張をさせるための気体の加熱に必要な熱源を高温熱源という。言葉通り、高温熱源の温度は、低温熱源の温度よりも高い。

熱効率

このように、サイクルとして繰り返し使用できる熱機関には、高温熱源と低音熱源の、温度の異なる2個の熱源が必要になる。

逆に言うと、たった一個の熱源だけでは、熱機関から仕事を取り出せない。このような原理を、熱力学の第2法則という。

仕事として取り出せるエネルギーWは、高温熱源で得た熱量Q₁のうち、低温熱源で捨てることになる熱量Q₂を引いた残りQ₁-Q₂である。

W=Q₁-Q₂

熱機関を動かすのに必要なエネルギーは、最低でも高温熱源の熱量Q₁は必要である。

熱機関が高温熱源から吸収した熱量の内、仕事に変えた割合を熱効率（thermal efficiency）といい

e={\frac {W}{Q_{1}}}

で表される。熱効率の式は100分率で表す場合もあり、その場合は上式の左辺を100倍すればよいだけである。本節では、100分率の表記は用いないとする。

熱効率eは、現実の機械では1より小さくなる。例外として、理論的な解析をする場合は、効率1の場合を含めて計算する場合もあるが、その場合でも、熱効率は1以下であり、1を超えることは無い。

熱効率の定義式に、W=Q₁-Q₂を代入すれば、

e={\frac {Q_{1}-Q_{2}}{Q_{1}}}

となる。

熱膨張率

物体は温度が上昇すると体積が膨張する。温度が1℃（あるいは1K）上昇するに連れて体積の増加する割合を体膨張率という。長さが、温度の1℃増加あたりに、長さの膨張する割合を線膨張率という。金属は熱伝導率が高い。中でも銀Agが最も高く、Cu、Au、Al、などがこれに次いでいる。線膨張率はプラスチックが最も高い。線膨張率をαとして、長さをL、加熱後の長さの変化量をΔL、加熱後の温度上昇をΔTとすると、定義より

{\frac {\Delta L}{L}}=\alpha \Delta T

の関係式が成り立つ。膨張量が小さい場合の近似式として、線膨張率αと体積膨張率βとの間に、以下の近似式が知られている。

\beta =3\alpha

.

導出

導出は、物体の体積をV、その変化量をΔVとすると、

V+\Delta V=\left(L+\Delta L\right)^{3}

および

V=L^{3}

の関係より、

1+{\frac {\Delta V}{V}}=\left(1+{\frac {\Delta L}{L}}\right)^{3}

さらに、近似式

\left(1+{\frac {\Delta L}{L}}\right)^{3}=1+3{\frac {\Delta L}{L}}

により、

1+{\frac {\Delta V}{V}}=1+3{\frac {\Delta L}{L}}

両辺から1を引き、この問題設定では体積膨張率βが、

\beta ={\frac {\Delta V}{V}}

であり、線膨張率αが

\alpha ={\frac {\Delta L}{L}}

なので、結局は

\beta =3\alpha

となる。（以上、導出。）

その他

状態量

気体の変数の変数p,V,Tは、理想気体であれ、ファンデルワールス気体であれ、状態方程式（理想気体かファンデルワールス気体かは、ここでは問わない）があるならば、変数p,V,Tのうちの、どれか二つが決まれば、気体の状態方程式から残りの変数も決まる。こうして3変数p,V,Tが決まる。

内部エネルギーは、理想気体であれ、ファンデルワールス気体であれ、どちらにしても、変数p,V,Tのうち、どれか二つが決まれば、気体の方程式から残りの変数も決まる。決まった3変数のp,V,Tによって、内部エネルギーも決まってしまう。このような、状態変数によってのみ決まる物理量を状態量（じょうたいりょう）という。 3変数のp,V,Tが決まれば内部エネルギーも決定されるので、内部エネルギーは状態量である。内部エネルギーを決める3変数のうち、真に独立変数なのは、そのうちの2個のみである。変数p,V,Tのどれを2個まで独立変数に選んでもいいが、残りの1個は既に選んだ変数の従属変数になる。

どの変数を独立変数に選ぶと、知りたい答えが求めやすいかは、問題による。

（多変数の関数の微分積分については、大学理科系で扱う。多変数関数の微分を偏微分という。解説は高校範囲を超える。）

等温変化

（この節では、高校数学III の微分積分を用いる。適宜該当教科を参照してください。）

圧力をpと書くとする。体積をV、モル数をn、普遍気体定数をR、温度を絶対温度でTとする。

仕事Wの、瞬間的な仕事の大きさは微分を用いてdWと表せる。体積Vの、その瞬間の体積変化は微分を用いてdVと表せる。これらを用いれば、

dW=pdV

と微分方程式で表せる。（定圧変化では無いから、この式のpは変数である。）

体積をV₁からV₂まで変化させた時の仕事は、積分を用いて以下のように書き表せる。

W=\int _{V_{1}}^{V_{2}}pdV

これに、状態方程式の pV = nRT を、組み合わせる。

積分変数のVに合わせて、pを書き換えよう。

p={\frac {nRT}{V}}

である。これより、仕事の式は、

W=\int _{V_{1}}^{V_{2}}pdV=\int _{V_{1}}^{V_{2}}{\frac {nRT}{V}}dV=nRT\int _{V_{1}}^{V_{2}}{\frac {dV}{V}}=nRT\log {\frac {V_{2}}{V_{1}}}

となる。（なお、logは自然対数である。）結論をまとめると、

W=nRT\log {\frac {V_{2}}{V_{1}}}

である。

内部エネルギーUは、理想気体では温度のみの関数で、等温変化では温度が変化しないから、

ΔU=0

である。

したがって、等温変化では

Q=W

である。

断熱変化

まず、熱と内部エネルギーと仕事の関係式

Q=U+W

を、次のように微分方程式に書き換える。内部エネルギーの変化を微小変化としてdUと表したとすると、熱量Qや仕事Wも微小変化になるので、以下の様な式になる。

d'Q=dU+d'W

QやWの微分演算記号dの上に点「'」が付いているのは、厳密に言うと、熱量Qや仕事Wは状態量で無いから、区別するために用いている。

断熱変化では

d'Q=0

なので、つまり、

0=dU+d'W

となる。

仕事に関しては

d'W=pdV

である。内部エネルギーの微小変化は、定積モル比熱を用いて、

dU=nC_VdT

と書ける。

なので、これ等を式 0=dU+d'W に代入し、

0=nC_VdT+pdV

と書ける。両辺をpVで割ると、

0={\frac {nC_{V}dT}{pV}}+{\frac {pdV}{pV}}={\frac {nC_{V}dT}{pV}}+{\frac {dV}{V}}

であるが、pV=nRTを利用すると、

0={\frac {nC_{V}dT}{nRT}}+{\frac {dV}{V}}={\frac {C_{V}}{R}}{\frac {dT}{T}}+{\frac {dV}{V}}

となる。

この微分方程式を解く。まず移項して、

{\frac {dT}{T}}=-{\frac {R}{C_{V}}}{\frac {dV}{V}}

となる。積分して、

\log T=-{\frac {R}{C_{V}}}\log {V}+Const

ここで、Constは積分定数とする。（積分定数を「C」と書かなかったのは、比熱の記号との混同を避けるため。）対数の性質より、係数R/Cvを対数log()の中の変数の指数に持ってこれる（数学II相当）ので、計算すると、

\log T=-\log {V^{\frac {R}{C_{V}}}}+Const

さらに移項して、変数を左辺にまとめると、

\log T+\log V^{\frac {R}{C_{V}}}=Const

対数の性質より、対数同士の和は、中の変数の積に変えられるので、

\log TV^{\frac {R}{C_{V}}}=Const

である。対数の定義より、自然対数の底をeとすれば

TV^{\frac {R}{C_{V}}}=e^{Const}

である。 e^Constを新しく、別の定数として、定数“constant”と置き直せば、

TV^{\frac {R}{C_{V}}}=constant

である。これで断熱変化の温度と体積の関係式の公式が求まった。

温度と体積の関係式

仕事Wとの関係を見たいので、先ほど求めた上の公式をpとTの式に書き換える事を考える。状態方程式pV=nRTを用いてTを、PとVを用いた式に書き換えると、まず代入しやすいように状態方程式を

T={\frac {pV}{nR}}

と書き換えて、これを公式に代入すれば、

TV^{\frac {R}{C_{V}}}={\frac {pV}{nR}}V^{\frac {R}{C_{V}}}={\frac {1}{nR}}pVV^{\frac {R}{C_{V}}}={\frac {1}{nR}}pV^{1+{\frac {R}{C_{V}}}}=constant

圧力と体積の関係式: ${\frac {1}{nR}}$ は定数なので、これを定数部にまとめてしまえば、別の定数をConst₂とでも置いて、; $pV^{1+{\frac {R}{C_{V}}}}=Const_{2}$

と書ける。ここで、指数部の式は、マイヤーの式Cp=Cv+Rより、定圧モル比熱で書き換えが可能である。

pV^{\frac {C_{p}}{C_{V}}}=Const_{2}

である。ここで、: ${\frac {C_{p}}{C_{V}}}$ を比熱比（ひねつひ、heat capacity ratio）と言う。比熱比の記号は一般にγで表す。これを用いると、

pV^{\gamma }=Const_{2}

である。

また、温度と体積の関係式

TV^{\frac {R}{C_{V}}}=constant

に比熱比を代入すると、

TV^{\gamma -1}=constant

になる。

これらの、圧力と体積の公式、および温度と体積の公式の二式をポアソンの式という。

カルノーサイクル

等温変化や断熱変化の考察で求まった公式を用いて、理論的な熱機関の、理論的な効率を調べよう。

まず、熱源として、高温熱源T1と低温熱源T2を用意する。熱サイクルとして、

高温熱源による等温膨張　→　断熱膨張　→　低温熱源による等温収縮　→　断熱圧縮

というサイクルを考える。

このようなサイクルをカルノーサイクル（Carnot cycle）という。

なお教育の都合上の話として、蒸気機関や自動車エンジンなどのように現実世界で制作される熱サイクルは、もっと複雑な過程になるが、しかし、いきなりそういうのを考えるのは複雑なので、まず、熱力学の教育では、カルノーサイクルを考えるのが、大学の理系の熱力学の教育では一般的である。

カルノーサイクルがなぜ、このようなサイクル形状なのかというと、まず高温熱源から熱を貰う間は、気体温度は高温熱源の温度と均衡してるとしているので、等温膨張とするのが妥当だろう。高温熱源から熱をもらい終わったあと、低温圧縮される前に、等温変化以外で仕事をして、内部気体の温度を低温熱源の温度まで下げるとするのが妥当である（収縮時も気体の温度が熱源と同じほうが理論的に扱いやすい）。等温変化の膨張のあとの変化は、あまり余計なエネルギー源を増やしたくないので、理論的に扱いやすいのは、断熱変化とするのが扱いやすいだろう。（もし定積変化や定圧変化にすると、機関が外部と仕事のやりとりをするため、つまり外部とエネルギーのやりとりをする事態になるので、変数が増えてしまい、計算が面倒になるだろう。）

ともかく、カルノーサイクルで行われる仕事を求めよう。

まず図の点1から点2の間の仕事W₁₂は等温膨張での仕事なので、高温熱源の温度をT₂とすれば、公式より、

W_{12}=nRT_{2}\log {\frac {V_{2}}{V_{1}}}

である。

図の点2から点3の間の仕事W₁₂は断熱膨張での仕事であり、ポアソンの公式W₁₂

pV^{\gamma }=K_{1}

より（K1は定数とする）、

W_{23}=\int _{V_{2}}^{V_{3}}pdV=K_{1}\int _{V_{2}}^{V_{3}}V^{-\gamma }dV={\frac {K_{1}}{1-\gamma }}[V^{1-\gamma }]_{V_{2}}^{V_{3}}

={\frac {K_{1}}{\gamma -1}}[V^{1-\gamma }]_{V_{3}}^{V_{2}}={\frac {K_{1}}{\gamma -1}}[{\frac {1}{V^{\gamma -1}}}]_{V_{3}}^{V_{2}}={\frac {K_{1}}{\gamma -1}}({\frac {1}{V_{3}^{\gamma -1}}}-{\frac {1}{V_{2}^{\gamma -1}}})={\frac {1}{\gamma -1}}(p_{3}V_{3}-p_{2}V_{2})={\frac {1}{\gamma -1}}(nRT_{1}-nRT_{2})

である。

図の点3から点4の間の仕事W₃₄は等温圧縮での負の仕事なので、低温熱源の温度をT₁とすれば、公式より、

W_{34}=nRT_{1}\log {\frac {V_{4}}{V_{3}}}=-nRT_{1}\log {\frac {V_{3}}{V_{4}}}

であり、この負の仕事の大きさと等量の熱を放出することになる。

図の点4から点1の間の仕事W₄₁は断熱圧縮での仕事であり、ポアソンの公式

pV^{\gamma }=K_{2}

より（K2は定数とする）、

W_{41}=\int _{V_{4}}^{V_{1}}pdV=K_{2}\int _{V_{4}}^{V_{1}}V^{-\gamma }dV={\frac {K_{2}}{1-\gamma }}[V^{1-\gamma }]_{V_{4}}^{V_{1}}

={\frac {K_{2}}{\gamma -1}}[V^{1-\gamma }]_{V_{1}}^{V_{4}}={\frac {K_{2}}{\gamma -1}}[{\frac {1}{V^{\gamma -1}}}]_{V_{1}}^{V_{4}}

={\frac {K_{2}}{\gamma -1}}({\frac {1}{V_{1}^{\gamma -1}}}-{\frac {1}{V_{4}^{\gamma -1}}})={\frac {1}{\gamma -1}}(p_{1}V_{1}-p_{4}V_{4})={\frac {1}{\gamma -1}}(nRT_{2}-nRT_{1})=-W_{23}

である。

機関が1サイクルの間にした仕事は、これ等を足し合わせれば良いから、

W_{12}+W_{23}+W_{34}+W_{41}

である。

このうち、

W_{23}=-W_{41}

なので、仕事として残る変数は、

W_{12}+W_{34}

であり、

W_{12}=nRT_{2}\log {\frac {V_{2}}{V_{1}}}

W_{34}=nRT_{1}\log {\frac {V_{4}}{V_{3}}}=-nRT_{1}\log {\frac {V_{3}}{V_{4}}}

だから、

W_{12}+W_{34}=nRT_{2}\log {\frac {V_{2}}{V_{1}}}-nRT_{1}\log {\frac {V_{3}}{V_{4}}}

である。これが、この機関が1サイクルで行う正味の仕事である。

ところで、 ${\frac {V_{2}}{V_{1}}}$ と、 ${\frac {V_{3}}{V_{4}}}$ の関係を求めよう。状態方程式pV=nRTより、

p_{1}V_{1}=p_{2}V_{2}

　　（1）

p_{3}V_{3}=p_{4}V_{4}

　　（2）

である。さらにポアソンの公式より、

p_{4}V_{4}{}^{\gamma }=p_{1}V_{1}{}^{\gamma }

　　（3）

p_{2}V_{2}{}^{\gamma }=p_{3}V_{3}{}^{\gamma }

　　（4）

である。これらを連立して解けば良い。計算の一例を示す。まず、式(1)と式(2)の左辺どうしと右辺どうしを掛ける。すると、

p_{1}p_{3}V_{1}v_{3}=p_{2}p_{4}V_{2}V_{4}

　　（5）

である。

今度は式(3)と式(4)の左辺どうしと右辺どうしを掛ける。すると、

p_{2}p_{4}V_{2}{}^{\gamma }v_{4}{}^{\gamma }=p_{1}p_{3}V_{1}{}^{\gamma }V_{3}{}^{\gamma }

　　（6）

である。

式(6)に式(5)を代入すると、式(6)の左辺は、

p_{2}p_{4}V_{2}{}^{\gamma }v_{4}{}^{\gamma }=(p_{2}p_{4}V_{2}V_{4})(V_{2}v_{4})^{\gamma -1}=(p_{1}p_{3}V_{1}v_{3})(V_{2}v_{4})^{\gamma -1}

　　（7）

式(6)の右辺は、

p_{1}p_{3}V_{1}{}^{\gamma }V_{3}{}^{\gamma }=(p_{1}p_{3}V_{1}v_{3})(V_{1}V_{3})^{\gamma -1}

　　（8）

となる。

式(7)=式(8)なので、

(p_{1}p_{3}V_{1}v_{3})(V_{2}v_{4})^{\gamma -1}=(p_{1}p_{3}V_{1}v_{3})(V_{1}V_{3})^{\gamma -1}

　　　（9）

である。これを整理して、

(V_{2}v_{4})^{\gamma -1}=(V_{1}V_{3})^{\gamma -1}

　　　　　　（10）

となる。これより、

(V_{2}v_{4})=(V_{1}V_{3})

　　　　（11）

である。さらに、求めたいのは、 ${\frac {V_{2}}{V_{1}}}$ と、 ${\frac {V_{3}}{V_{4}}}$ の関係であったから、式(10)を移行すれば、

{\frac {V_{2}}{V_{1}}}={\frac {V_{3}}{V_{4}}}

　　　　　（12）

が求まる。なぜ、式(12)を求めたかというと、そもそもの目的は、正味の仕事

W_{12}+W_{34}=nRT_{2}\log {\frac {V_{2}}{V_{1}}}-nRT_{1}\log {\frac {V_{3}}{V_{4}}}

　　　　（13）

を求めるためであったので、では、正味の仕事を求めよう。

式(12)より、式(13)を変形できて、

W_{12}+W_{34}=nR(T_{2}-T_{1})\log {\frac {V_{2}}{V_{1}}}

　　　　（14）

と書ける。

これが、カルノーサイクルの、1サイクルでの正味の仕事である。

カルノーサイクルの効率

まず、自動車エンジンの熱サイクルは、カルノーサイクルではない。

熱サイクルは、カルノーサイクルの他にも、さまざまな形がある。

自動車エンジンどうしの熱サイクルですら、ガソリンエンジンの熱サイクルとディーゼルエンジンの熱サイクルは、別々の形であるし、それらの熱効率の公式の具体形も違ってくる。このように、具体的な熱サイクルの違いによって、それぞれ熱効率の公式も具体的な形が違う。

高校生は、まずは学習の基準としてカルノーサイクルの場合の熱効率の理論上の公式を導出してみよう。（また、後述の節にある「エントロピー」などの計算でも、カルノーサイクルをもとに計算をするので、まず、カルノーサイクルを学ぼう。）

では、これからカルノーサイクルの理論上の仕事効率の公式を探求しよう。

（※ 図では、x軸変数がPになっているが、x軸変数をPにするか、それともVにするかは、あまり本質的なことではないので、読者には容赦を願いたい。PVグラフの座標軸のとりかたは、分野によってはx軸が場合もあれば、別の分野ではx軸がVの場合もあり、分野ごとに異なっており、統一してない。）

カルノーサイクルが高温熱源から受け取る熱量Q1は、行程1→2であり、この行程は等温変化なので、受け取った熱量はすべて仕事になっている。行程1→2での等温変化の仕事は、

W_{12}=nRT_{2}\log {\frac {V_{2}}{V_{1}}}

であったので。これが高温熱源から受け取った熱量Q1に等しい。つまり

Q_{1}=nRT_{2}\log {\frac {V_{2}}{V_{1}}}

である。

熱効率eの式は、高温熱源から受け取った熱量をQとして、正味の仕事をWとすれば、

e={\frac {W}{Q}}

であった。これに、既に求めた、熱量Q₁とW₁₂を代入すれば、

e={\frac {W}{Q}}={\frac {nR(T_{2}-T_{1})\log(V_{2}/V_{1})}{nRT_{2}\log(V_{2}/V_{1})}}

である。これを約分して整理すれば、

e={\frac {T_{2}-T_{1}}{T_{2}}}

である。これがカルノーサイクルの理論上の最高効率である。このカルノーサイクルの最高効率は、絶対温度だけで決まる。実際の熱機関の効率は、不可逆変化（ふかぎゃくへんか、irreversible change）を含み、これよりも低くなるので、現実の熱効率まで式に含めたければ、不等号を用いて表せば良い。式を書くと

e

≦

{\frac {T_{2}-T_{1}}{T_{2}}}

となる。

注意事項

カルノーサイクルの最大効率のこの公式 $e={\frac {T_{2}-T_{1}}{T_{2}}}$ は、あくまで熱サイクルの形がカルノーサイクルな場合のみの公式である。

サイクルがカルノーサイクル以外の場合については、上記の式変形では、何の導出・証明もできていない。

もし読者が、カルノーサイクル以外の熱サイクルの場合に、最大の効率の式を求めたいなら、効率の定義式 $e={\frac {W}{Q_{1}}}$ または式変形した $e={\frac {Q_{1}-Q_{2}}{Q_{1}}}$ に戻って、計算しなおす必要がある。

カルノーサイクルでない、自動車エンジンでのp,v,Tの変化をもとに考案された熱サイクルが、すでに工学などで提案されており、たとえばオットーサイクル（ガソリンエンジンの熱サイクル）やディーゼルサイクルなど（ディーゼルエンジンのサイクル）がある。

オットーサイクルやディーゼルサイクルの理論上の最大効率の式も、 $e={\frac {Q_{1}-Q_{2}}{Q_{1}}}$ をもとにした効率の公式がすでに提案されている。

なお一般に、熱機関で理論上の効率が最大効率になりうる場合は、あくまで、まず、その熱機関の動かし方が可逆であり、さらに熱機関を準静的に動かした場合である。そもそも現実の自動車エンジンは可逆・準静的には運動してるとは言いづらいという現実にも、気をつける必要があるだろう。

その他（※ 範囲外）

また、上記の議論をみるかぎり、「熱サイクルの形がカルノーサイクルの形に近いかどうか」は、効率の高低とは無関係である。

そもそも、どんな形の熱サイクルも、図のように、複数個のカルノーサイクルの組み合わせに分解できる。右図の例のように、ゆがんだ丸型のサイクルですら、複数個のカルノーサイクルの組み合わせに分解できる。

もし仮に、1個のカルノーサイクルに形が近いことで熱効率が高くなると仮定したら、では、どんな形の熱サイクルもカルノーサイクルの組み合わせに分解できるというグラフ上の事実をどう考えるのか？

エントロピー

熱の伝わりとエントロピー

自然界では、外部からエネルギーを加えないかぎり、高温物体から接触した低温物体には熱が伝わり、高温物体から熱が失われただけ、高温物体の温度が下がっていき、逆に低温物体が得た熱のぶんだけ低温物体の温度は上がっていき、最終的に両物体（元・高温物体と元・低温物体）の温度は等しくなる。

その逆の現象（低温物体から高温物体に熱が伝わり、高温物体はますます高温になり、低温物体はますます低温になる現象）は存在しない。

このような、高温物体から低温物体に熱がつたわる現象を、数式で調べてみよう。

まず、図のように、床の上にある高温物体に接触した低温物体に、熱が伝わる場合を考える。高温物体も低温物体も静止してるとしよう。

床は熱を伝えにくい物体で作られているとする。問題の簡単化のため、高温物体の熱は低温物体にのみ伝わり、他の場所には拡散しないとしよう。（たとえば、空気中への熱の拡散は、無視する。）

このとき、高温と低温の定義により、

T_{h}

≧

T_{c}

である。

まず、高温熱源の温度をT_hと書くとしよう。また、低温熱源の温度はT_cと書くとしよう。

すると、高温物体が失った熱量のぶんだけ、低温物体は熱量を得るので、両物体の変化した熱量の大きさは同じである。

つまり、高温熱源の熱量の変化の大きさを Q_h として、また、低温熱源の熱量の変化の大きさを Q_c とすれば、

|Q_h|＝|Q_c|

である。（記号 |　| は絶対値の記号。）

簡単化のため

|Q_h|＝|Q_c|＝Q

と書くしよう。

さて、天下り的だが、

S={\frac {Q}{T}}

という量を考える。

量Sは、それぞれの物体ごとに考える必要があり、

S_{1}={\frac {Q_{h}}{T_{h}}}

および

S_{2}={\frac {Q_{c}}{T_{c}}}

という物理量をそれぞれ考える必要がある。

すごく天下り的だが、この量 S₁ および S₂ は、足しあわせられるとしよう。

（※ つまり、いわゆる「示量性」（しりょうせい）の変数だとしよう。たとえば、質量は、示量性の変数である。質量1kg物体の物体Aと、質量2kgの物体を同時に重量計に乗せれば、重量計の示す数値として、質量は3kg（＝1kg＋2kg）を示す。

いっぽう、温度は、示量性の変数ではない。温度20℃の水に、温度40℃の湯をまぜても、けっして温度60℃にはならない。）

さて、とにかく、この量 S₁ および S₂ は、足しあわせる。

すると、系全体では、この量は、

S_{1}+S_{2}={\frac {Q_{h}}{T_{h}}}+{\frac {Q_{C}}{T_{c}}}

になる。

このとき、

|Q_h|＝|Q_c|＝Q

といった仮定があったので、この仮定にもとづき、さきほどの式（S1＋S2）にあるQhとQcに、それぞれQを代入すれば、

S_{1}+S_{2}={\frac {-Q}{T_{h}}}+{\frac {Q}{T_{c}}}

となる。

上式では、高温物体からは熱量が失われるので、負号（ー）を付けた。

さらに、

T_{h}

≧

T_{c}

の関係を思い出し、

さきほどの式と連立させると、

{\frac {-Q}{T_{h}}}+{\frac {Q}{T_{c}}}=Q({\frac {-1}{T_{h}}}+{\frac {1}{T_{c}}})=Q({\frac {-T_{c}}{T_{h}T_{c}}}+{\frac {T_{h}}{T_{h}T_{c}}})=Q({\frac {-T_{c}+T_{h}}{T_{h}T_{c}}})

≧ 0

である。

つまり、

S_{1}+S_{2}={\frac {-Q}{T_{h}}}+{\frac {Q}{T_{c}}}

≧ 0

つまり、物理量 S_1 + S_2 は、時間経過とともに、かならず増える。

{\frac {Q}{T}}

はエントロピー（entropy）と呼ばれる物理量である。エントロピーの記号はSと置くとする。また、エントロピーの単位はJ/Kである。

つまり、エントロピーは、かならず増える。

熱効率とエントロピー

熱効率の定義式と、カルノーサイクルの熱効率の温度の関係式を連立させてみよう。まず、高温熱源の温度をT_hと書くとして、高温熱源から熱機関に渡す熱量をQ_hと書くとしよう。低温熱源の温度はT_cとして、熱機関から低温熱源に放熱される熱量をQ_cと書くとしよう。熱効率eの定義式は、

e={\frac {Q_{h}-Q_{c}}{Q_{h}}}

であった。いっぽう、カルノーサイクルの熱効率は、

e

≦

{\frac {T_{h}-T_{c}}{T_{h}}}

である。

これらより、

{\frac {Q_{h}-Q_{c}}{Q_{h}}}

≦

{\frac {T_{h}-T_{c}}{T_{h}}}

である。これは、

1-{\frac {Q_{c}}{Q_{h}}}

≦

1-{\frac {T_{c}}{T_{h}}}

とも書けて、両辺の1を引いて消去して、

-{\frac {Q_{c}}{Q_{h}}}

≦

-{\frac {T_{c}}{T_{h}}}

となる。マイナスがあるので、移項すれば、

{\frac {T_{c}}{T_{h}}}

≦

{\frac {Q_{c}}{Q_{h}}}

である。添字が同じ量どうしをまとめれば、

{\frac {Q_{h}}{T_{h}}}

≦

{\frac {Q_{c}}{T_{c}}}

　　　　　　（1）

となる。ここで、 ${\frac {Q}{T}}$ を新しい物理量として定義して、この量はエントロピー（entropy）と呼ばれる。エントロピーの記号はSと置くとする。つまり、

S={\frac {Q}{T}}

である。そうすると、式(1)は

S_{h}

≦

S_{c}

　　　　　　（2）

と書ける。

熱機関の動作の順序は、まず機関が高温熱源から熱を貰ってから、低温熱源に熱を渡すのであった。（逆に先に低音熱源に放熱してから高温熱源で吸熱するのは不可能である。熱機関は、もらってない熱は渡せない。熱力学の第二法則より当然である。）だから、時間的には、熱機関のエントロピーSは、まず先にS=S_hになってから、時間が経って、あとからS=S_cになったのである。そして式(2)より、 $S_{h}$ ≦ $S_{c}$ 　であるから、熱機関のエントロピーは、時間が経って、増大したことが分かる。

以上の論証より、熱機関のエントロピーは、かならず増大する。これをエントロピー増大の法則という。

熱が伝わる現象にせよ、熱機関の現象にせよ、エントロピーは、かならず増加する。このように、自然界ではエントロピー増大の法則が成り立っている。

溶液とエントロピー

『高等学校化学I/溶液の性質』と関連あり。

元には戻らない現象も「エントロピー」と言うのだったら、だったら、

絵の具（えのぐ）を水にとかす事だって、エントロピーではないか？

という疑問が、わいてくるかもしれない。

化学では、溶質が溶液にとける事について、「エントロピー」と表現する場合もある。（※ なお、絵の具（えのぐ）は溶質ではないので、間違えないように。絵の具は、水に溶けない。もし、絵の具が水に溶けてしまったら、無色透明になってしまい、絵の具としての効果がない。）

また、この化学における溶質と溶液のエントロピーは、なんと数値的な計算が可能である。

説明の簡単化のため、不揮発性の溶質だとしよう。

熱力学における「エントロピー」とは、エネルギーを、絶対温度で割り算した値だった。

凝固点降下や沸点上昇をもとに、エネルギーを計算できる。なぜなら、比熱 C に、上昇または降下したぶんの温度 ΔT を掛ければいいだけであるから。

そして、その時の絶対温度 T は、その実験のときの溶液の温度をもとに、簡単に計算できる。たとえば、水の沸点上昇なら、T＝373 K (＝273＋100)というふうに、簡単に計算できる。

つまり、

（CΔT）/T

が、溶質によるエントロピー変化である。

このように、化学では、エントロピーは、相変化（そうへんか）において、ひとつの計算方法を提供する。

ところで、分母Tが絶対零度の場合、つまり 0ケルビンの場合は、どうなるかというと、実はこれは、「量子力学」（りょうしりきがく）という分野が関わってくる、高校レベルを大幅に超えた、かなり専門的な話題になるので、高校レベルでは説明を省略する。

※ なお、合金（ごうきん）のように、ある固体（仮にAとする）と別の固体（仮にBとする）が混合している場合にも、それぞれの純金属の場合とは熱力学的な性質が少々、違っている場合があるので、熱力学における「エントロピー」を計算できる場合もある。しかし、高校レベルを大幅に超えた、かなり専門的な話題になるので、高校レベルでは説明を省略する。

拡散とエントロピー

溶質が溶液にとけるときに、溶質が水中を広がっていくだろう。

熱も、温度の高い場所から、温度の低い場所へと広がっていく。

すると、エントロピーとは、熱や温度と関係のある現象をおこす何かが、不可逆的に広がっていく性質について、言及しているとも言えそうである。

溶質が溶液に溶けるという現象も、熱や温度と関係のある現象である。なぜなら、凝固点という温度を降下させたりするように、温度と関係のある現象を起こすので。

なお、物理学や数学では、なにかが広がっていく現象のことを「拡散」（かくさん）という。

ならば、この拡散という用語を用いて、エントロピーとは何だろうかの説明を次のように言い換えよう。

エントロピーとは、熱や温度と関係のある現象をおこす何かが、不可逆的に拡散している性質について、言及しているとも言えそうである。

固体のモル比熱

固体の（化合物や合金でない）単体元素の1モルあたりの定積モル比熱は、おおよそ一定値になり、

おおよそ

Cv ＝ 24～30[J/mol・K] である。

とくに、かなりの単体元素が、

Cv ＝ 24～26[J/mol・K] である。

（ただし、いくつか例外的に、当てはまらない元素もある。C（炭素）やBe（ベリリウム）やケイ素、ホウ素など。)

また、気体定数Rやボルツマン定数k_Bを使えば

C_{V}=3R=3Nk_{\mathrm {B} }=25.5

[J/mol・K]

と近似できる。

これを、デュロン＝プティの法則という。

（※ 例外）ただし、極低温の付近になると、合わなくなる。（※ 大学の量子力学で、の理論を習う。）極低温の場合は、「アインシュタインの比熱式」になる。

また、（大学ではロクに習わないが、）合金になると、合わなくなる。

こうなる理論的考察は、定説では量子力学の理論を使うとされており、大学レベルになるので、説明を省略する。

なお、二原子分子の場合、たとえば NaClのモル比熱は約 50 [J/mol・K]であり、約 6R ＝ 2×3R の値になっている。

酸化銅 CuO のモル比熱は約42 [J/mol・K] と、若干、小さい。

気体分子にしろ、固体にしろ、比熱は、モル比熱で考えると、それぞれ、常温付近では、（例外的ないくつかの元素固体を除くと）元素の種類によらず、ほぼ一定値になることが分かる。（大学では極低温などの例外ばかりが強調されるが、しかし常温では多くの元素で十分にデュロン＝プティの法則は成り立っている。）

また、それらのモル比熱は、気体定数Rを使った式で簡潔に近似することができる。

こういう実験事実が、モルの概念の有用性や、気体の状態方程式の有用性の裏付けになっている。

なお液体の場合には、デュロン＝プティの法則のような関係は特に見つかってない。

固体の比熱の法則には、例外は少ないが、しかし固体の比熱の法則のほうは（当てはまらない元素が多いなどのように）例外が比較的に多い。そういう事情もあってか、物理学の熱力学での「エネルギー等分配の法則」の理論が、気体を基準にして法則を導き出してから固体の比熱を考察していく理論体系になっていることも妥当であろう（例外の多い「固体」比熱よりも、例外の少ない「気体」比熱のほうが、法則に近いと考えるのは妥当だろうという事である）。

エネルギー等分配の法則

速度について、

{\bar {v^{2}}}={\bar {v_{x}{}^{2}}}+{\bar {v_{y}{}^{2}}}+{\bar {v_{z}{}^{2}}}

であったから、運動エネルギーについても、

{\frac {1}{2}}m{\bar {v^{2}}}={\frac {1}{2}}m{\bar {v_{x}{}^{2}}}+{\frac {1}{2}}m{\bar {v_{y}{}^{2}}}+{\frac {1}{2}}m{\bar {v_{z}{}^{2}}}

である。これに、単原子分子理想気体の内部エネルギーの式

U={\frac {1}{2}}Nm{\bar {v{}^{2}}}={\frac {3}{2}}NkT

とを合わせて、運動エネルギーは各方向成分を求める。各方向とも等分されるのが妥当なので、したがって、各方向の運動エネルギーは

{\frac {1}{2}}m{\bar {v_{x}{}^{2}}}={\frac {1}{2}}m{\bar {v_{y}{}^{2}}}={\frac {1}{2}}m{\bar {v_{z}{}^{2}}}={\frac {1}{2}}kT

となる。

このことから、運動の自由度１個につき、エネルギーが ${\frac {1}{2}}kT$ ずつ等分される事がわかる。これをエネルギー等分配の法則（law of equi-paritation of energy）という。

2原子分子では、運動の自由度は、分子速度の3方向に加えて、回転運動が2個、加わる。二つの分子を結ぶ軸に垂直な方向の平面上の線が回転軸の方向になるので、面の自由度2個が加わる。よって、2原子分子（diatomic molecule）では、理想気体の内部エネルギーの式は、

U={\frac {1}{2}}m{\bar {v^{2}}}=5{\frac {1}{2}}kT={\frac {5}{2}}kT

になる。 2原子分子の内部エネルギーが ${\frac {5}{2}}kT$ になることは、実験的にも比熱の測定によって確認されている。

ここまでで、高校物理の熱力学での発展的話題は終了である。これより先の水準の話題は、大学での範囲になる。

^ 単位に注意。 $\mathrm {J=N\cdot m=Pa\cdot m^{3}=10^{3}\,Pa\cdot L}$
^ ここでは、重力の影響は無視して考えている。
^ ボルツマン定数は単に $k$ とも表される。
^ $mN_{\mathrm {A} }$ は 1 mol の分子の質量を kg で表したものである。分子量 M は 1 mol の分子の質量を g で表したものだから、 $10^{3}$ の係数が必要になる。
^ ピストン外とシリンダー内の圧力が違うとすると、ピストンはなめらかに動く(=ピストンとシリンダー間の摩擦が存在しない)ため、ピストンが動いてしまう。

[1] 単位に注意。 $\mathrm {J=N\cdot m=Pa\cdot m^{3}=10^{3}\,Pa\cdot L}$

[2] ここでは、重力の影響は無視して考えている。

[3] ボルツマン定数は単に $k$ とも表される。

[4] $mN_{\mathrm {A} }$ は 1 mol の分子の質量を kg で表したものである。分子量 M は 1 mol の分子の質量を g で表したものだから、 $10^{3}$ の係数が必要になる。

[5] ピストン外とシリンダー内の圧力が違うとすると、ピストンはなめらかに動く(=ピストンとシリンダー間の摩擦が存在しない)ため、ピストンが動いてしまう。

[1]

[2]

[3]

[4]

[5]