高校物理 電磁気学

高等学校の学習 > 高等学校理科 > 高等学校 物理 > 高校物理 電磁気学

電気

クーロン力(静電気力)

離れた2個の無限に小さい帯電体(点電荷)の間に働く力をクーロン力(静電気力)といい，原点に点電荷$Q$があるとき，そこから${\overrightarrow {r}}$の位置に置かれた点電荷$q$の受ける力${\overrightarrow {F}}$は

${\overrightarrow {F}}=k{\frac {Qq}{r^{2}}}\left(\!{\frac {\overrightarrow {r}}{r}}\!\right)$ (1.1)

である。$k$はクーロン力の比例定数とよばれ，$k={\frac {1}{4\pi \varepsilon _{0}}}\fallingdotseq 8.99\times 10^{9}\,\ \mathrm {N\cdot m^{2}/C^{2}}$である($\varepsilon _{0}$：真空の誘電率)。

$F>0$ のときは、$Q,\ q$ は同符号なので、点電荷に働く力は斥力であり、$F<0$ のときは、$Q,\ q$ は異符号なので、点電荷に働く力は引力である。

電場

帯電体がある空間に、電荷を置くとその電荷は静電気力を受ける。これは帯電体が空間に影響を与え、電荷に力が加わったと考えることができる。このように、静電気力がはたらく空間の状態を電場(電界)という。

空間内の位置${\overrightarrow {r}}$に置いた十分小さい電荷$q$が力${\overrightarrow {F}}({\overrightarrow {r}})$を受けたならば，その位置の電場は単位電荷あたりの力，すなわちベクトル

${\overrightarrow {E}}({\overrightarrow {r}})={\frac {{\overrightarrow {F}}({\overrightarrow {r}})}{q}}$(1.2)

で与えられる。(1.2)を変形すると

${\overrightarrow {F}}({\overrightarrow {r}})=q{\overrightarrow {E}}({\overrightarrow {r}})$. (1.2)$'$

(1.2)$'$は，電場${\overrightarrow {E}}({\overrightarrow {r}})$中で点${\overrightarrow {r}}$に置かれた電荷$q$が受ける力を指す。この小電荷$q$を試験電荷という。

点電荷の作る電場

正電荷の周りの電荷の向き

以上のように定義された電場がどのように生み出されるのかについて考えよう。静止した点電荷$Q$があったとき，$Q$はそこから${\overrightarrow {r}}$の位置に

${\overrightarrow {E}}({\overrightarrow {r}})={\frac {{\overrightarrow {F}}({\overrightarrow {r}})}{q}}=k{\frac {Q}{r^{2}}}\left(\!{\frac {\overrightarrow {r}}{r}}\!\right)$ (1.3)

の電場を生み出す。電場の大きさは

$E=k{\frac {|Q|}{r^{2}}}$ (1.3)$'$

である。

重ね合わせの原理

電場の重ね合わせ

${\overrightarrow {r}}$の位置に複数の点電荷がつくる電場${\overrightarrow {E}}({\overrightarrow {r}})$は，それぞれの点電荷がつくる電場${\vec {E_{i}}}({\overrightarrow {r}})$のベクトル和である。

${\overrightarrow {E}}({\overrightarrow {r}})=\sum _{i}{\vec {E_{i}}}({\overrightarrow {r}})$. (1.4)

電気力線

電気力線とは電場の方向を接線とする曲線である。

電場に垂直な平面を貫く電気力線の単位面積あたりの本数は、電場の強さの値と等しいものとする。

電気力線には、以下のような性質がある。

• 正電荷から出て負電荷に入る
• 電場が強い場所では密である

物理基礎で扱った静電誘導・静電遮蔽・誘導分極は、電気力線を用いることでベクトルの引き算として説明することができる。

一般に、閉曲面を貫く電気力線の本数は不変である。

例） 全体に強さEの電場が一様に掛けられた半径rの球の中心に電気量Qの点電荷を置く。
クーロンの法則の比例定数をkとすると電場の強さは$E=k{\frac {Q}{r^{2}}}$である。よって、球面のうち表面積が1m²の領域を貫く電気力線の本数は$k{\frac {Q}{r^{2}}}$本である。
球の表面積は$4\pi r^{2}$であるので、球面全体を貫く電気力線の本数は$k{\frac {Q}{r^{2}}}\cdot 4\pi r^{2}=4\pi kQ$と求まる。この式に半径rは含まれないので、電気力線の本数は閉曲面の形状に依らないことがわかる。

ここで、誘電率εを$\varepsilon ={\frac {1}{4\pi k}}$と定義すると、この事実は以下のように表せる。

誘電率εの空間に置かれた電気量Qの電荷を囲む閉曲面を貫く電気力線の本数は、常に${\frac {Q}{\varepsilon }}$である。(ガウスの法則)

クーロンの法則の比例定数kに物理定数としての名前がついていないのは、誘電率と定数のみを用いて表すことができるからである。

なお、真空中で考えるとき、クーロンの法則の比例定数と誘電率はそれぞれ$k_{0},\varepsilon _{0}$と置かれることが多い。

ガウスの法則を用いると、電場の強さEは閉曲面の表面積をSとして、$E={\frac {Q}{\varepsilon S}}$と表せる。

• 等電位面

電位

電場中に置かれた電荷が静電気力(クーロン力)を受けて運動するとき，静電気力は電荷に対して仕事する。静電気力は保存力なので，その仕事は重力がする仕事と同様，始点と終点の位置によって決まり，途中の経路によらない。したがって，重力と同様に静電気力による位置エネルギーが定義できる。電場において，重力場における「高さ」に対応する概念が電位である。

$xy$平面を水平面に，鉛直上向きに$z$軸をとり，$-z$方向を向いた一様な電場${\overrightarrow {E}}=(0,\ 0,\ -E)$を考える。この電場から電荷$q$の受ける力は$q{\overrightarrow {E}}$，これに逆らって電荷をゆっくり運ぶ力は$-q{\overrightarrow {E}}=(0,\ 0,\ qE)$．この電荷が$r$の位置で持つ位置エネルギーは，この力$-q{\overrightarrow {E}}$で$q$を基準点(原点O)から${\overrightarrow {r}}$まで運ぶ仕事でそれは運ぶ経路によらず$U({\overrightarrow {r}})=-q{\overrightarrow {E}}\cdot {\overrightarrow {r}}=qEz$．そこで電位を単位電荷あたりの位置エネルギー

$V({\overrightarrow {r}})=U({\overrightarrow {r}})\div q=Ez$

で定義する。

重力が等高面(位置エネルギー一定の面)に垂直で下(位置エネルギーの低くなる向き)を向いているのと同様，電場は等電位面に垂直で電位の低くなる向きを向いている。

一般の静電場の場合も同様で，$r$位置で電荷$q$がもつ位置エネルギーが，電場から受ける$q{\overrightarrow {E}}$に逆らって$-q{\overrightarrow {E}}$を加え，基準点${\vec {r_{0}}}$からその点${\overrightarrow {r}}$まで電荷をゆっくり運ぶ仕事

$U_{\mathrm {C} }({\overrightarrow {r}})=\int _{r_{0}}^{r}-q{\overrightarrow {E}}\cdot d{\overrightarrow {r}}=-q\int _{r_{0}}^{r}{\overrightarrow {E}}\cdot d{\overrightarrow {r}}$ (1.5)

で定義される。静電気力が保存力であるためこの積分は${\vec {r_{0}}}$から${\overrightarrow {r}}$への経路によらない。そこで，電位を単位電荷あたりの静電気力による位置エネルギー

$V({\overrightarrow {r}})={\frac {U({\overrightarrow {r}})}{q}}=-\int _{r_{0}}^{r}{\overrightarrow {E}}\cdot d{\overrightarrow {r}}$ (1.6)

で定義する。つまり，ある点の電位とは，基準点からその点まで電荷をゆっくり運ぶために外力が単位電荷あたりにせねばならぬ仕事のことである。この定義より質量$m$，電荷$q$の粒子に対する電場中でのエネルギー保存則は次のように表される。

${\frac {1}{2}}mv^{2}+qV=$一定．(1.7)

また定義より，電荷$q$を電場の力$q{\overrightarrow {E}}$に抗して${\vec {r_{1}}}$から${\vec {r_{2}}}$まで運ぶために外力のする仕事$W_{\mathrm {EF} }$は

$W_{\mathrm {EF} }=q(V({\vec {r_{2}}})-V({\vec {r_{1}}}))=-q\int _{\vec {r_{1}}}^{\vec {r_{2}}}{\overrightarrow {E}}\cdot d{\overrightarrow {r}}$ (1.8)

で与えられる。この$V({\vec {r_{2}}})-V({\vec {r_{1}}})$を電位差又は電圧という。つまり２点間の電位差(電圧)とは電場に抗して電荷をその２点間で運ぶために単位電荷あたり要する仕事である。

点電荷$Q$が原点にあるときの電位を求めよう。このとき電場は(1.3)で与えられるから，(1.6)は

$V({\overrightarrow {r}})=-\int _{r_{0}}^{r}k{\frac {Q}{r^{2}}}{\frac {({\overrightarrow {r}}\cdot dr)}{r}}=-\int _{r_{0}}^{r}k{\frac {Q}{r^{2}}}dr=kQ\left({\frac {1}{r}}-{\frac {1}{r_{0}}}\right)$

となる。基準点を無限遠($r_{0}\to \infty$)にとると，点電荷$Q$がとる電場の電位は

$V({\overrightarrow {r}})=k{\frac {Q}{r}}$. (1.9)

コンデンサー

コンデンサーの充電の仕組み

図のように2枚の金属板を平行に向かい合わせて、電源をつなげると、自由電子が導線を通り金属板に電荷が蓄えられる。

平行板コンデンサーの2つの金属板にそれぞれ $Q,\ -Q$ の電荷が蓄えられているとき、極板間の電位差 $V$ は次の関係がある。

$Q=CV$

ここで、$C$ をコンデンサーの電気容量という。 電気容量の単位はファラド $\mathrm {F}$ が使われる。

平行板コンデンサーの電気容量

平行板コンデンサーの電場

極板の間隔 $d$ で面積 $S$ の平行板コンデンサーの電気容量 $C$ を求める。

コンデンサーに電荷 $Q$ が蓄えられているとき、極板間の電位差を $V$ とする。このとき、極板間の電場 $E$ は $E={\frac {V}{d}}$ である。

極板から出る電気力線の本数 $N$ は $N=SE=S{\frac {V}{d}}$ である。

また、ガウスの法則より、 $N={\frac {Q}{\varepsilon }}$ である。

すなわち、電気力線の本数について

$N={\frac {Q}{\varepsilon }}=S{\frac {V}{d}}$

より、 $C={\frac {Q}{V}}=\varepsilon {\frac {S}{d}}$ を得る。

コンデンサーの蓄えるエネルギー

電気容量 $C$ のコンデンサーが $Q$ の電荷を蓄え、極板間の電位差が $V$ のとき、コンデンサーの蓄えるエネルギー $U$ を求める。

コンデンサーに電荷 $Q'$ の電荷が蓄えられたとき、極板間の電位差は $V'={\frac {Q}{C}}$ である。この状態で微小電荷 $dQ'$ を運ぶために必要な仕事は $V'dQ'={\frac {Q'}{C}}dQ'$ である。これを $Q'$ が 0 から $Q$ になるまで積分すればコンデンサーの蓄えるエネルギー $U$ が求まる。

$U=\int _{0}^{Q}{\frac {Q'}{C}}dQ'=[{\frac {Q'^{2}}{2}}]_{0}^{Q}={\frac {1}{2}}{\frac {Q^{2}}{C}}$

したがって、$U={\frac {1}{2}}{\frac {Q^{2}}{C}}={\frac {1}{2}}CV^{2}={\frac {1}{2}}QV$ である。

コンデンサーの接続

コンデンサーを並列につなげたとき、このコンデンサー全体としてみたときの電気容量を求める。

電気容量 $C_{1},\,C_{2}$ の電気容量を並列につなげ、電圧 $V$ の電源をつなげる。

それぞれのコンデンサーに蓄えられる電荷 $Q_{1},\,\ Q_{2}$ は

$Q_{1}=C_{1}V,\,Q_{2}=C_{2}V$ である。

コンデンサーが蓄えた電荷の合計は $Q_{1}+Q_{2}=C_{1}V+C_{2}V=(C_{1}+C_{2})V$ である。

コンデンサー全体としてみたときの合成電気容量 $C$ について $Q_{1}+Q_{2}=CV$ となるので、これと比較して

$C=C_{1}+C_{2}$

を得る。

コンデンサーを直列につなげたとき、このコンデンサー全体としてみたときの電気容量を求める。

電気容量 $C_{1},\,C_{2}$ の電気容量を直列につなげ、電圧 $V$ の電源をつなげる。2つのコンデンサーが蓄える電荷は等しいので、これを $Q$ とする。それぞれのコンデンサーの電圧 $V_{1},\ V_{2}$ は

$V_{1}={\frac {Q}{C_{1}}},\,V_{2}{\frac {Q}{C_{2}}}$

である。この和が電源の電圧 $V$ に等しいので

$V=V_{1}+V_{2}={\frac {Q}{C_{1}}}+{\frac {Q}{C_{2}}}$

コンデンサー全体としてみたときの合成電気容量 $C$ は $V={\frac {Q}{C}}$ となるので、これと比較して

${\frac {1}{C}}={\frac {1}{C_{1}}}+{\frac {1}{C_{2}}}$

である。

金属板や誘電体を差し込んだコンデンサー

誘電体の誘電率 $\varepsilon$ と真空の誘電率 $\varepsilon$ の比 $\varepsilon _{\mathrm {r} }={\frac {\varepsilon }{\varepsilon _{0}}}$ を比誘電率という。

真空中で極板面積 $S$、極板間隔 $d$ の平行板コンデンサーの電気容量 $C_{0}$ は $C_{0}=\varepsilon _{0}{\frac {S}{d}}$ である。

このコンデンサーの極板間に比誘電率 $\varepsilon _{\mathrm {r} }$ の誘電体をすきまなく挿入したとき、コンデンサーの電気容量 $C$ は

$C=\varepsilon _{\mathrm {r} }\varepsilon _{0}{\frac {S}{d}}=\varepsilon _{\mathrm {r} }C_{0}$

である。

直流回路

電流

導体断面を単位時間あたりに通過する電気量(電荷)を電流(英: electric current)という〔単位：A(アンペア)〕。時刻$t$において，電気量を$Q(t)$とすると，微小時間${\mathit {\Delta }}t$間に電荷が$Q(t+{\mathit {\Delta }}t)-Q(t)$通過するとき，電流$I(t)$は

$I(t)=\lim _{{\mathit {\Delta }}t\to 0}{\frac {Q(t+{\mathit {\Delta }}t)-Q(t)}{{\mathit {\Delta }}t}}={\frac {dQ(t)}{dt}}$

である。また，断面積$S$〔m$^{2}$〕，単位体積あたりの自由電子数が$n$〔個/m$^{2}$〕の導体を電流が流れるとき，その電流の大きさ$I$〔A〕は電気素量を$e$〔C〕，自由電子の速さを$v$〔m/s〕として

$I=enSv$〔A〕

である。

電池の内部抵抗

電池の内部にもわずかに電気抵抗は存在する。これを電池の内部抵抗という。

起電力 $E$ 、内部抵抗 $r$ の電池に電流 $I$ が流れるとき、電池の端子電圧 $V$ は、内部抵抗による電圧降下は $rI$ であるから

$V=E-rI$

である。

ジュール熱と消費電力

電圧を$V$，電流を$I$とすると，単位時間あたりの発熱量(ジュール熱)$P$は

$P=IV$.

起電力$E$、内部抵抗$r$の電池に$R$の抵抗をつなぐとき、抵抗での電位差$V$はオームの法則より$V=RI$，回路に流れる電流$I$は$I={\frac {E}{r+R}}$であるから、抵抗での消費電力 $P$ は

$P=RI^{2}={\frac {RE^{2}}{(r+R)^{2}}}$

である。

ここで、$R$ を変えたときの消費電力$P$の最大値を求める。

$P={\frac {RE^{2}}{(r+R)^{2}}}={\frac {E^{2}}{{\frac {r^{2}}{R}}+2r+R}}\cdots \cdots (*)$

• 解１

$(*)$の両辺を$R$で微分すると

${\frac {dP}{dR}}={\frac {-E^{2}(-{\frac {r^{2}}{R^{2}}}+1)}{({\frac {r^{2}}{R}}+2r+R)^{2}}}={\frac {E^{2}(r^{2}-R^{2})}{(r^{2}+2Rr+R^{2})^{2}}}={\frac {E^{2}(r-R)}{(r+R)^{3}}}$.

${\frac {dP}{dR}}=0$のとき

$R=r$.

よって$R>0$における$P$の増減表は以下のようになる。

${\begin{array}{c|c}R&(0)\cdots \;r\;\cdots \\\hline {\frac {dP}{dR}}&\quad \ +\ \ 0\ \ -\\\hline P&\quad \ \nearrow {\frac {E^{2}}{4r}}\searrow \\\end{array}}$ よって，$R=r$のとき極大値${\frac {E^{2}}{4r}}$をとる。

• 解２

相加平均・相乗平均より

${\frac {r^{2}}{R}}+R\geq 2{\sqrt {{\frac {r^{2}}{R}}\cdot R}}=2r$. (等号成立は ${\frac {r^{2}}{R}}=R$ すなわち $R=r$ のとき)

つまり、 $R=r$ で ${\frac {r^{2}}{R}}+R$ は最小値 $2r$ を取る。すなわち、$P={\frac {E^{2}}{{\frac {r^{2}}{R}}+R+2r}}$ は最大値 ${\frac {E^{2}}{4r}}$ を取る。

キルヒホッフの第１法則

任意の結接点において，流入電流の和は流出電流の和に等しい。

$\sum _{\mathrm {inflow} }I_{i}=\sum _{\mathrm {outflow} }I_{i'}'$.

キルヒホッフの第２法則

任意の閉回路に対して，起電力(英: electromotive force)の和は電圧降下(英: voltage drop)の和に等しい。

$\sum _{\mathrm {closed\ circuit} }V_{\mathrm {emf} }=\sum _{\mathrm {closed\ circuit} }V_{\mathrm {drop} }$.

半導体

必要があれば高等学校 化学基礎及び高等学校 化学を参照。

半導体の種類

半導体は、導体と絶縁体の中間の通電性を持つ物質である。珪素（シリコン）はその代表格である。

珪素(Si)の結晶はダイヤモンド型共有結合結晶であり、非常に硬く熱に強い。そのため、セラミックとして様々な用途で用いられる。（人工衛星の外壁、庖丁、陶器etc.）詳しくは無機化学を参照。ゲルマニウム(Ge)も共有結合結晶をつくる元素である。Si、Geともに価電子数は4で、これらを互いに共有することによって共有結合をなす。

SiやGeは、常温では抵抗率が大きく通電性が低いものの、高温下では自由電子が生じて通電性が高まる。このような半導体を真性半導体という。真性半導体に微量の不純物を入れると、通電性が高まる。このような半導体を不純物半導体という。

電流の担い手をキャリアという。

真性半導体に微量のアルミニウム(Al)やインジウム(In)などを混ぜたものをp型半導体という。AlやInは価電子を3つしか持たないので、共有結合をするには電子が一個不足し、電子のない所ができる。これを正孔（ホール）という。電場を与えると、電子が移動して正孔を埋める。移った電子がいたところが新たな正孔となるのでまた別の電子が移動し・・・と繰り返すことによりホールが電場の向きに移動し、電流の担い手となる。よって、p型半導体のキャリアは正孔である。p型のpは正孔が正電荷(positive charge)であることに由来する。

真性半導体に微量の燐(P)やアンチモン(Sb)などを混ぜたものをn型半導体という。PやSbは価電子を5つ持つので、4つが共有結合に加わり1つ余ってしまう。この余った1つは結晶を自由に動き回ることによって電流の担い手となる。よって、n型半導体のキャリアは電子である。n型のnは電子が負電荷(negative charge)であることに由来する。

ダイオード

p型とn型を接合（pn接合）し、両端に電極をつけた部品を半導体ダイオードという。接合した面を接合面という。

半導体ダイオードは一方向にのみ電流を流す作用(整流作用)を持つ。整流作用は、交流電流から直流電流への変換や、AEDが電気ショック前に行う充電などに応用されている。

ダイオードの順方向に電圧を加えると、電場によってp型の中の正孔がn型へ、n型の中の電子がp型へ引かれ、pn接合面で一対づつ結合して消える(再結合)。その一方で、電極からはキャリアが供給され続ける。よって、電流が流れ続ける。

ダイオードの逆方向に電圧を加えると、電場によってp型の中の正孔はp型側の電極へ、n型の中の電子はn型側の電極へ引かれ、p型で負電荷、n型で正電荷が過剰になってpn接合部付近においてp型とn型の間に電位差が生じる。このとき、電流は止まる。pn接合面付近にキャリアが殆ど存在しない領域が発生し、この領域を欠乏層という。

半導体に光が当たると半導体を構成する原子から電子が離れ、正孔が生まれる。このとき、pn接合面付近に電位差が生まれるのでn型側の電極に電子、p型側の電極に正孔が集まる。よって、p型が正極、n型が不極の電池となる。このような仕組みの電池を太陽電池という。

太陽電池とは逆に電気を光に変換する半導体部品を発光ダイオードという。砒化ガリウム(GaAs)のような半導体のpn接合に順方向の電圧を加えると、キャリアが再結合する際に発光する。発光ダイオードは太陽電池と同様に光を当てると起電力を生じる。このとき、発光する色と同色の光を当てると起電力が大きくなる。

トランジスタ

電気信号を増幅する働き（増幅作用）を持つ電子部品をトランジスタという。

トランジスタは3つの不純物半導体を組合せた部品であり、p型2つの間にn型を挟んだpnp型トランジスタとn型2つの間にp型を挟んだnpn型トランジスタが存在する（pnp型はバイポーラートトランジスタともいう）。トランジスタを構成する3つの部分をそれぞれエミッタ(E)、ベース(B)、コレクタ(C)という。

npn型のC-E間に電圧を加えた状態でE-B間に順方向の電圧を加えると、EからBに向かってキャリアが送り込まれ、その大部分はCへと流れ込む。よって、Bの電極に流れる電流はCの電極に流れる電流よりも非常に大きな値となる。これを利用すると、B電流の小さな変化をC電流の大きな変化に変換できる。pnp型でも同様にして増幅作用を確かめられる。

トランジスタは、B電流の制御によりCに電流が流れる状態(ON)と全く流れない状態(OFF)を作ることができる。これをトランジスタのスイッチング作用という。

C電流のON-OFFによってデジタル信号を作り出すことができ、計算等の処理を電気回路で行うことができる。

LSI

コンピュータの黎明期には、トランジスタに相当するものとして真空管が用いられていた。これは当時画期的な電子部品だったが、真空管を用いたコンピュータは耐久性が低く、発熱しやすく、装置が巨大になるという欠点を抱えていた。

真空管に代わってトランジスタが用いられるようになると、コンピュータの小型化と演算回路の高速化が進んだ。

その後、多数のトランジスタやコンデンサー、抵抗などの電気素子を小さな基盤上に集積した集積回路(IC)が発明されると、コンピュータの小型化と高性能化は怒濤の早さで進んだ。1000個以上の素子を集積したICを特に大規模集積回路(LSI)というが、2024年現在では10億を超えるトランジスタを実装したLSIが量産されている。

集積回路内の回路素子は、半導体である珪素(Si)が酸化されると絶縁体(SiO₂)に変わるという性質を利用している。シリコンウエハースを局所的に酸化し、微小領域を絶縁体で囲む。この中にp型・n型の領域を形成すると、互いに絶縁された多数の微小トランジスタが出来上がる。同じ表面にコンデンサーや抵抗も形成し、これらを配線することでICが完成する。

LSIの高機能化・高性能化・低消費電力化を実現するには、より微細な回路素子を高密度に集積することが求められる。処理工程の精密な制御技術と回路パターン形成のための精密な写真技術の進歩により、2024年現在では30nmを下回る寸法の回路パターンを持つものも量産されている。

LSIはCPU・RAMの主用部品だが、それ以外にも多様な部品に使われている。高速応答性が要求される領域では、砒化ゲルマニウム(GeAs)やガリウムインジウムリン(InGaP)といったシリコン以外の半導体を使ったLSIも用いられている。

磁気

以下では磁気を扱う。その際外積(ベクトル積)を用いることがあるので必要に応じて参照されたい。

磁気力と磁場

磁石に鉄粉をかけると磁石の両端によく付着する。この鉄粉を吸引する力の原料力とみられる部分(最も強い部分)を磁石の磁極という。磁極どうし或いは磁石どうし，電流どうし，電流と磁石が互いに引き合い或いは斥け合う力のことを磁気力(磁力)という。磁極の強さを表す量を磁気量〔Wb〕という。

電場が電荷に力を及ぼす空間の性質である一方，磁場(磁界)は運動している電荷に力を及ぼす空間の性質である。磁場は電場と同様に，大きさと向きを持つベクトルである。磁場ベクトル${\overrightarrow {H}}$の点に，磁気量$m$〔Wb〕の磁極を置いたとき，この磁極に働く力を$F$〔N〕とすると

${\overrightarrow {H}}={\frac {\overrightarrow {F}}{m}}$〔N/Wb〕(2.1)

が成り立つ。

磁束密度

磁束密度を${\overrightarrow {B}}$とおくと，磁場${\overrightarrow {H}}$と真空の透磁率$\mu _{0}$を用いると

${\begin{aligned}{\overrightarrow {B}}&=\mu _{0}{\overrightarrow {H}}\\&={\frac {\mu _{0}{\overrightarrow {F}}}{m}}\ (\because (2.1))\end{aligned}}$(2.2)

と表される。なお，この磁束密度${\overrightarrow {B}}$のことを単に磁場と呼ぶこともある。

真空の透磁率は$\mu _{0}=1.26\times 10^{-6}\fallingdotseq 4\pi \times 10^{-7}$[N/A²]である。物質の比透磁率は$\mu _{r}={\frac {\mu }{\mu _{0}}}$で求められる。地球大気の比透磁率はほぼ1であり、鉄の比透磁率は8000である。

電流が作る磁場

電流${\overrightarrow {I}}$の流れている導線Cを微小区間に分割する。電流によって作り出される磁場を定めているビオ・サヴァールの法則(英: Biot–Savart law)により，位置${\vec {r'}}$にある微小区間$dl$の電流が位置${\overrightarrow {r}}$に作る磁束密度は

$d{\overrightarrow {B}}({\overrightarrow {r}})={\frac {\mu _{0}}{4\pi }}\cdot {\frac {{\overrightarrow {I}}\times ({\overrightarrow {r}}-{\vec {r'}})}{|{\overrightarrow {r}}-{\vec {r'}}|^{3}}}dl$. (2.3)

電流全体の作る磁束密度は全微小区間からの寄与を足し合わせれば，つまり積分すれば求まる。

${\overrightarrow {B}}({\overrightarrow {r}})={\frac {\mu _{0}}{4\pi }}\int {\frac {{\overrightarrow {I}}\times ({\overrightarrow {r}}-{\vec {r'}})}{|{\overrightarrow {r}}-{\vec {r'}}|^{3}}}dl$. (2.4)

無限に長い直線電流

無限に長い直線電流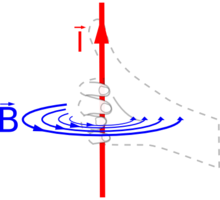

右ねじの法則

右図のように，電流にそって$z$をとり，磁場を求める点Pを通るように$x$軸をとると$({\overline {\mathrm {OP} }}=r)$，$xyz$空間において${\overrightarrow {r}}=(r,\ 0,\ 0).\ {\vec {r'}}=(0,\ 0,\ z')$とおくと$z$軸上の微小区間$[z',\ z'+dz']$の電流が点Pに作る磁束密度は外積の性質より${\overrightarrow {I}}$と${\overrightarrow {r}}-{\vec {r'}}$に垂直，すなわち

$d{\overrightarrow {B}}({\overrightarrow {r}})=(0,\ dB(r),\ 0)$

と$y$成分のみで，$|{\overrightarrow {r}}-{\vec {r'}}|={\sqrt {r^{2}+{z'}^{2}}}$であるから

$dB(r)={\frac {\mu _{0}}{4\pi }}{\frac {I\sin \theta }{r^{2}+{z'}^{2}}}dz'={\frac {\mu _{0}I}{4\pi }}{\frac {rdz'}{(r^{2}+{z'}^{2})^{\frac {3}{2}}}}$.

よって電流全体が作る磁束密度$B$は(2.4)より

$B(r)={\frac {\mu _{0}I}{4\pi }}\int _{-\infty }^{\infty }{\frac {rdz'}{(r^{2}+{z'}^{2})^{\frac {3}{2}}}}$.

ここで，$z'=r\tan \phi$とすると

${\frac {dz'}{d\phi }}=r{\frac {\cos ^{2}\phi -\sin \phi (-\sin \phi )}{\cos ^{2}\phi }}={\frac {r}{\cos ^{2}\phi }}\quad \therefore dz'={\frac {rd\phi }{\cos ^{2}\phi }}\quad {\begin{array}{c|c}z'&-\infty \to \infty \\\hline \phi &-{\frac {\pi }{2}}\to {\frac {\pi }{2}}\\\end{array}}$

であるから(置換積分)

$B(r)={\frac {\mu _{0}I}{4\pi }}\int _{-{\frac {\pi }{2}}}^{\frac {\pi }{2}}{\frac {r{\frac {rd\phi }{\cos ^{2}\phi }}}{(r^{2}+r^{2}\tan ^{2}\phi )^{\frac {3}{2}}}}={\frac {\mu _{0}I}{4\pi }}\int _{-{\frac {\pi }{2}}}^{\frac {\pi }{2}}{\frac {\cos \phi }{r}}d\phi ={\frac {\mu _{0}I}{4\pi r}}[\sin \phi ]_{-{\frac {\pi }{2}}}^{\frac {\pi }{2}}={\frac {\mu _{0}I}{2\pi r}}$.

以上より直線電流が作る磁束密度は電流まわりに渦巻き状に分布し，電流から垂直距離$r$離れた位置では

大きさ：$B(r)={\frac {\mu _{0}I}{2\pi r}}\Longleftrightarrow H(r)={\frac {I}{2\pi r}}\ (\because (2.2))$ (2.5)

向き：$I$に垂直な面内で$I$に対して右回り(右ねじの法則)

円形電流

半径rの円形導線に大きさIの電流が流れるとき、円の中心での磁場の強さHは$H={\frac {I}{2r}}$と表される。

導出は直線電流の場合と同様である。

ソレノイド

導線を密に巻いた十分に長い円筒状のコイルをソレノイドという。

ソレノイドの作る磁場は、一定の間隔で並ぶ円形電流が周囲に作る磁場の重ね合わせと考えると、$H=nI$と求まる。但し、nはコイルの単位長さあたりの巻数である。

磁場が電流に及ぼす力

フレミングの左手の法則

磁束密度(磁場)${\overrightarrow {B}}$が長さ$l$の電流${\overrightarrow {I}}$に及ぼす力(電磁力，アンペール力)${\overrightarrow {F}}$は

${\overrightarrow {F}}=l{\overrightarrow {I}}\times {\overrightarrow {B}}$

と表され，磁束密度${\overrightarrow {B}}$と電流${\overrightarrow {I}}$のなす角を$\theta$として外積の性質より

大きさ：$F=lIB\sin \theta$ (磁場${\overrightarrow {H}}$と真空の透磁率$\mu _{0}$を用いると(2.2)より$F=\mu _{0}lIH\sin \theta$)

向き：フレミングの左手の法則に従う，或いは電流の向きと磁場の向きに垂直に立てた右ねじを電流の向きから磁場の向きに回したときに右ねじの進む向き

2つの平行電流が及ぼしあう力を求めてみよう。

十分に長い2本の平行導線P,Qをr[m]だけ離し、それぞれに大きさI₁,I₂の電流を流す。電流の向きが等しいとき、PがQのl[m]の部分に及ぼすアンペール力は、$F=I_{2}B_{1}l=I_{2}{\frac {\mu I_{1}}{2\pi r}}l={\frac {\mu I_{1}I_{2}}{2\pi r}}l$と求まる。このとき、QがPのl[m]の部分に及ぼすアンペール力はFと同じ大きさで同じ向きである。

電流の向きが反対のとき、及ぼしあうアンペール力の向きも反対となる。

ローレンツ力

一般に荷電粒子が磁場を横切ると，磁場から力を受けることが知られている。電場${\overrightarrow {E}}$，磁束密度${\overrightarrow {B}}$の中で，速度${\overrightarrow {v}}$，電荷$q$の荷電粒子に働く力

${\overrightarrow {F}}=q({\overrightarrow {E}}+{\overrightarrow {v}}\times {\overrightarrow {B}})$，

特に磁束密度${\overrightarrow {B}}$の中で速度${\overrightarrow {v}}$，電荷$q$の荷電粒子に働く力

${\overrightarrow {F}}=q{\overrightarrow {v}}\times {\overrightarrow {B}}$

をローレンツ力(英: Lorentz force)という。磁束密度${\overrightarrow {B}}$と速度${\overrightarrow {v}}$のなす角を$\theta$として外積の性質より

大きさ：$F=qvB\sin \theta$

向き：フレミングの左手の法則に従う，或いは正電荷のときに荷電粒子の速度の向きと磁場の向きに垂直に立てた右ねじを速度の向きから磁場の向きに回したときに右ねじの進む向き(負電荷では逆になる)

サイクロトロン・ベータトロン

磁束

閉曲線Cの正の向きを定め，その向きに右ねじを回してねじが進む向きにCの囲む面の法線ベクトル${\overrightarrow {n}}$をとる。Cの囲む面の面積を$S$としてCを貫く磁束${\mathit {\Phi }}$は

${\mathit {\Phi }}=\int {\overrightarrow {B}}\cdot {\overrightarrow {n}}dS$

特に${\overrightarrow {B}}\cdot {\overrightarrow {n}}$が一様であるときは

${\mathit {\Phi }}={\overrightarrow {B}}\cdot {\overrightarrow {n}}S=BS\cos \theta$.

電磁誘導

誘導起電力

コイルの両端に検流計を繋ぎ、棒磁石をコイルに近づけたり遠ざけたりすると検流計の針が振れる。このように、閉回路を貫く磁場（磁束）の時間変化によって閉回路に電圧が生じて電流を生ずる現象を電磁誘導という。生じた電圧を誘導起電力、電流を誘導電流という。

誘導起電力は以下のレンツの法則に従う。

誘導起電力は、誘導電流による磁束が外部から加えられた磁束変化を妨げる方向に発生するような向きに生じる。

具体例）鉛直に立てられたコイルに棒磁石のN極を近づけると、磁束の増加する方向（鉛直下向き）とは逆向き（鉛直上向き）の磁束が発生する向き（時計回り）に誘導電流が流れる。

イギリスのファラデーは、実験を通して「コイルに発生する誘導起電力の大きさはコイルを貫く磁束の単位時間あたりの変化量とコイルの巻数に比例する」という事実を発見した。これを定式化したのが、次のファラデーの電磁誘導の法則である。

$V=-N{\frac {\Delta \Phi }{\Delta t}}$

負の符号は、レンツの法則による。また、Nはコイルの巻数である。

一般に、誘導起電力$V_{\mathrm {emf} }$は

$V_{\mathrm {emf} }=-{\frac {d{\mathit {\Phi }}}{dt}}$.

と表される。

電磁誘導は、コイルを磁場に出し入れする場合も起こる。

長さlの導線が磁束密度Bの磁場を速さvで横切り、磁場ベクトルと導線の速度ベクトルのなす角度がθであるとき、誘導起電力は以下の式で表される。

$V_{\mathrm {emf} }=l({\vec {v}}\times {\vec {B}})=vBl\sin \theta$

無限に長い2本の導線に起電力$V_{0}$の電池と抵抗値$R$の抵抗を直列に繋げ、長さ$l$の軽い導線を乗せる。磁束密度$B$の磁場を回路に垂直にかけ、乗せた導線に質量$m$の錘をつけて速さ$v$で引き上げる。

導線の両端に生じる誘導起電力は、$\sin 90^{\circ }=1$より$vBl$である。レンツの法則より誘電起電力の向きは電池の向きと逆なので、回路に流れる電流の大きさを$I$とするとキルヒホッフの第二法則より$V_{0}-vBl=RI$である。

時間をtとしてItを両辺にかけるて変形すると、$IV_{0}t=vtIBl+I^{2}Rt$。導線と錘は等速運動をするので、重力加速度を$g$とするとローレンツ力と重力の釣り合いより$IBl=mg$である。導線と錘の移動距離$vt$を$h$とおくと、最終的にこのような式となる。

$IV_{0}t=mgh+RI^{2}t$

左辺は電池のする仕事、右辺は重力による位置エネルギーと抵抗で発生するジュール熱である。

このように、誘電起電力が発生する場合もエネルギー収支を考えることが可能である。

なお、導線の速さが変化する場合でも、レンツの法則より速度変化を妨げる向きに誘導起電力が発生するため、最終的に等速運動となる。

交流

交流の発生

コイルの回転 実効値 変圧器

交流回路

交流における電流・電圧・抵抗 コイルのリアクタンス・消費電力 コンデンサーのリアクタンス・消費電力 インピーダンス 共振 電気振動