高等学校数学I/2次関数

高等学校の学習 > 高等学校数学 > 高等学校数学I > 2次関数

関数

f(x)

一般に、$y$が$x$の関数である場合に、 $f$ などの文字を用いて、

$y=f(x)$

と書き表すことができる。

また、x の関数 y＝f(x) のことを単に f(x) と省略して言う場合もよくある。

関数 y＝f(x) において、変数xの値をaにした場合の関数の値を f(a) で表す。

つまり、関数f(x) の x＝a の場合でのyの値が f(a) である。ちなみに関数のfとは 英語で関数を意味するfunctionの頭文字 からとった

象限

xy座標で第1象限（しょうげん）から第4象限までの位置を、図のように定義する。

位置と象限の番号の対応の覚え方は、x軸の正方向を基準に、反時計周り（左回り）に番号が大きくなっていくと覚えればいい。

それぞれの象限と、X、Yの値との関係は、左図のとおり。

2次関数

定義

2次関数の定義

定数 $a\neq 0$ と、定数 $b$, $c$を用いて $y=ax^{2}+bx+c$ と $x$ の二次式で表す事ができる関数を変数 $x$ の2次関数という。

具体例

以下の関数はいずれも2次関数である。

• $y=3x^{2}+4x+1$　　　　　($a=3$、$b=4$、$c=1$の場合に相当)
• $y=x^{2}-4x$　　　　　($a=1$、$b=-4$、$c=0$の場合に相当)
• $y=-x^{2}$　　　　　($a=-1$、$b=0$、$c=0$の場合に相当)

一方以下の関数は2次関数ではない

• $y=4x+1$

読者はこれを当然と思うかもしれないが、上の式は

$y=0x^{2}+4x+1$

と表記することもできる。しかし、これは $x$ 二次式ではないので2次関数ではない。 そのために、2次関数の定義において$a\neq 0$でなければならないというルールを設けたのである。

2次関数のグラフ

y=ax² のグラフ

まず、もっとも簡単な$y=ax^{2}$のグラフは$a>0$ のとき図1のようになる。（図では$a=1$の場合を表記）。また、$a<0$ のときは図1 のグラフを上下さかさまにしたものになる。

図1 (y=x²のグラフ)

$a>0$ のとき2次関数 $y$ は 下に凸 （したにとつ）といい、$a<0$ のとき 上に凸 （うえにとつ）という。また、2次関数のグラフを放物線という。

y=ax² + q のグラフ

2つの2次関数

y ＝ 2x²　　　　(1)

y ＝ 2x²＋4　　　　(2)

のグラフを書くために値を求めると、下記の表のようになる。

x	…	-3	-2	-1	0	1	2	3	…
2x2	…	18	8	2	0	2	8	18	…
2x2＋4	…	22	12	6	4	6	12	22	…

表を見ると、(2)　2x²+4　の値は、つねに (1)　2x² の値よりも4だけ大きい。

したがって(2)　2x²+4　のグラフは、 (1)　2x² のグラフをy軸方向に4だけ平行移動した放物線であり、

軸がy軸

頂点が 点(0, 4)

の放物線である。

一般に y＝ax2＋q のグラフは、 y＝ax2 のグラフをy軸方向に q だけ平行移動した放物線であり、 軸はy軸、　　頂点は　点 (0, q)　である。

y=a(x-p)² のグラフ

y＝2(x-3)²　のグラフは、　2x² のグラフをx軸方向に3だけ平行移動した放物線であり、

軸は 直線 x＝3

頂点は 点(3, 0)

の放物線である。

一般に y＝a(x-p)2 のグラフは、 y＝ax2 のグラフをx軸方向に p だけ平行移動した放物線であり、 軸は 直線 x＝p 、　　頂点は　点 (p, 0)　 である。

y=a(x-p)² +q のグラフ

y＝2(x-3)²＋4　のグラフは、　y＝2(x-3)² のグラフをy軸方向に4だけ平行移動した放物線である。

そして、y＝2(x-3)² のグラフは　y＝2x² のグラフをx軸方向に3だけ平行移動した放物線であったので、つまり

y＝2(x-3)²＋4　のグラフは、y＝2x² のグラフを x軸方向に3, y軸方向に4, 平行移動した放物線である。

よって、

軸は直線 x＝3

頂点は 点(3, 4)

である。

一般に y＝a(x-p)2＋p のグラフは、 y＝ax2 のグラフをx軸方向に p, y軸方向にq , 平行移動した放物線であり、 軸は 直線 x＝p 、　　頂点は　点 (p, q)　 である。

y=ax² + bx +c のグラフ

一般形と標準形

本節では2次関数の一般形と標準形について学ぶ。この知識は後で2次関数をグラフで表す際に役立つ。

先ほど現れた

$y=ax^{2}+bx+c$

という形の式 ($a\neq 0$) を2次関数の一般形といい、

$y=a(x-p)^{2}+q$

という式を2次関数の標準形という。 （上で、$a\neq 0$、$b$、$c$、$p$、$q$は定数で、$x$は変数であるものとする。）

一般形と標準形の関係

定理 2次関数の一般形は必ず2次関数の標準形に変形することができ、逆に2次関数の標準形は必ず2次関数の一般形に変形することができる。

一般形で表記されている2次関数を標準形で表記する事を平方完成という。 後述するように、標準形は2次関数をグラフで表す際に用いる。

証明

標準形

$y=a(x-p)^{2}+q$

で表記されている2次関数の右辺を展開すると、

$y=ax^{2}-2apx+(ap^{2}+q)$

となるので、

$b=-2ap,\quad c=ap^{2}+q$

とすれば一般形になる。

逆に一般形

$y=ax^{2}+bx+c$

で表記されている2次関数は以下の手順で標準形に変換できる（この変形手法を平方完成という）。

$y=ax^{2}+bx+c$

$=a\left(x^{2}+{\frac {b}{a}}x\right)+c$

$=a\left\{x^{2}+{\frac {b}{a}}x+\left({\frac {b}{2a}}\right)^{2}-\left({\frac {b}{2a}}\right)^{2}\right\}+c$

$=a\left\{x^{2}+{\frac {b}{a}}x+\left({\frac {b}{2a}}\right)^{2}\right\}-{\frac {b^{2}}{4a}}+c$

$=a\left(x+{\frac {b}{2a}}\right)^{2}-{\frac {b^{2}-4ac}{4a}}$

ここで、

$p=-{\frac {b}{2a}},\quad q=-{\frac {b^{2}-4ac}{4a}}$

とおくと、

$y=a(x-p)^{2}+q$

となり標準形で表されたことになる。

例題

例題

次の2次関数が一般形ならば標準形に、標準形ならば一般形にせよ。

1. $y=2(x+4)^{2}+4$
2. $y=4x^{2}+12x+9$
3. $y=x^{2}+5x$

解

1. $y=2x^{2}+16x+36$
2. $y=4\left(x+{\frac {3}{2}}\right)^{2}$
3. $y=\left(x+{\frac {5}{2}}\right)^{2}-{\frac {25}{4}}$

一般の2次関数のグラフ

一般の2次関数をグラフで表現してみよう。 前述のように2次関数は平方完成の手順を踏む事により必ず標準形で表記可能なので、2次関数$y=ax^{2}+bx+c$を標準形

$y=a(x-p)^{2}+q$

に変換する。ここで、

$p=-{\frac {b}{2a}},\quad q=-{\frac {b^{2}-4ac}{4a}}$

この標準形のグラフは$y=ax^{2}$ のグラフを $x$ 軸方向に　$p$, $y$ 軸方向に $q$ 平行移動させたものと考えることができる。よって以下の事実が結論付けられる。

2次関数のグラフ

定理 2次関数 $y=ax^{2}+bx+c$ のグラフは軸が$x=-{\frac {b}{2a}}$ , 頂点が $\left(-{\frac {b}{2a}},-{\frac {b^{2}-4ac}{4a}}\right)$ であるような放物線である。

※ 参考

グラフの平行移動

2次関数にかぎらず、一般に関数 y＝f(x) のグラフをy軸の正の方向に q だけ平行移動したグラフは、 関数　 y ＝ f(x) ＋q のグラフになる。 また、関数 y＝f(x) のグラフをx軸の正の方向に p だけ平行移動したグラフは、 関数　 y ＝ f(x－p) のグラフになる。 よって、関数 y＝f(x) のグラフをx軸の正の方向に p 、y軸の正の方向にq だけ平行移動したグラフは、 関数　 y ＝ f(x－p) ＋q のグラフになる。

グラフの対称移動

2次関数にかぎらず、一般に関数 y＝f(x) のグラフをx軸に関して対称に移動したグラフは、 関数　 y ＝ －f(x) のグラフになる。 また、関数 y＝f(x) のグラフをy軸に関して対称に移動したグラフは、 関数　 y ＝ f(－x) のグラフになる。 よって、関数 y＝f(x) のグラフを原点に関して対称に移動したグラフは、 関数　 y ＝ － f(－x) のグラフになる。

例題

例題

2次関数 $y={\frac {1}{2}}x^{2}+3x+{\frac {1}{2}}$ のグラフをかけ。

解

${\begin{matrix}y&=&{\cfrac {1}{2}}x^{2}+3x+{\cfrac {1}{2}}\\[10pt]{}&=&{\cfrac {1}{2}}(x+3)^{2}-4\end{matrix}}$

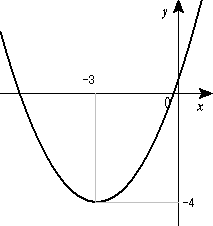
ゆえに、求めるグラフは軸 $x=-3$、頂点 $(-3,-4)$ の下に凸な放物線である。

例題

2次関数 $y=4x^{2}+20x+4$ のグラフは $y=4x^{2}$ のグラフをどのように平行移動させたものか。

解

${\begin{matrix}y&=&4x^{2}+20x+4\\{}&=&4\left(x+{\frac {5}{2}}\right)^{2}-21\end{matrix}}$

であるので、$y=4x^{2}$ のグラフを $x$ 軸方向に $-{\frac {5}{2}}$、$y$ 軸方向に -21 移動させたものである。

2次関数のグラフと二次方程式

2次関数$y=ax^{2}+bx+c$のグラフと$x$軸に共有点があるとき、その共有点の$y$座標は0であるから、共有点の$x$座標は、二次方程式$ax^{2}+bx+c=0$の実数解である。

• 問題例

• • 問題

次の2次関数のグラフと$x$軸の共有点の座標を求めよ。
(i)

$y=x^{2}-2x-1$

(ii)

$y=-4x^{2}-4x-1$

• • 解答

(i)　2次方程式$x^{2}-2x-1=0$を解くと

$x={\frac {-(-2)\pm {\sqrt {(-2)^{2}-4\times 1\times (-1)}}}{2\times 1}}={\frac {2\pm {\sqrt {8}}}{2}}={\frac {2\pm 2{\sqrt {2}}}{2}}=1\pm {\sqrt {2}}$

よって、共有点の座標は

$\left(1+{\sqrt {2}}\ ,\ 0\right)\ ,\ \left(1-{\sqrt {2}}\ ,\ 0\right)$

(ii)　2次方程式$-4x^{2}-4x-1=0$を解くと

$4x^{2}+4x+1=0$

$(2x+1)^{2}=0$

$x=-{\frac {1}{2}}$

よって、共有点の座標は

$\left(-{\frac {1}{2}}\ ,\ 0\right)$

(ii)のグラフはただ1点$\left(-{\frac {1}{2}}\ ,\ 0\right)$で共有し、共有点の$x$座標は二次方程式$-4x^{2}-4x-1=0$の重解である。このようなとき、2次関数のグラフは$x$軸に接するといい、その共有点を接点という。

2次関数$y=ax^{2}+bx+c$のグラフと$x$軸との共有点の$x$座標は、二次方程式$ax^{2}+bx+c=0$の実数解で、実数解の個数は$D=b^{2}-4ac$の符号によって決まる。

$b^{2}-4ac$ のことを 2次方程式 $ax^{2}+bx+c=0$の 判別式 （はんべつしき）という。

※ 「D」とは「判別式」を意味する discriminant の頭文字である。

Dの符号	D>0	D=0	D<0
a ＞ 0 のとき
a ＜ 0 のとき
共有点の個数	2個	1個	0個

2次関数のグラフと$x$軸の位置関係

2次関数$y=ax^{2}+bx+c$のグラフと$x$軸の位置関係について、$D=b^{2}-4ac$とするとき $D>0\quad \Longleftrightarrow \quad$ 異なる2点で交わる $D=0\quad \Longleftrightarrow \quad$ 1点で接する $D<0\quad \Longleftrightarrow \quad$ 共有点をもたない

例題

• • 問題

次の2次関数のグラフと$x$軸との共有点の個数を求めよ。

(I)

$y=3x^{2}-x+3$

(II)

$y=-2x^{2}-3x+5$

(III)

$y=x^{2}-2{\sqrt {3}}x+3$

• • 解答

(I)

$D=(-1)^{2}-4\times 3\times 3=-35<0$

だから、$x$軸との共有点はなし。
(II)

$D=(-3)^{2}-4\times (-2)\times 5=49>0$

だから、$x$軸との共有点は2個。
(III)

$D=(2{\sqrt {3}})^{2}-4\times 1\times 3=0$

だから、$x$軸との共有点は1個。

定義域と値域

定義域と値域

2次間数にかぎらず、一般に関数 y ＝ f(x)において、

変数x のとりうる値の範囲のことを定義域（ていぎいき、domain）という。

また、xの値に対応して y の値のとりうる範囲のことを値域（ちいき、range）という。

多くの場合、値域は定義域の影響を受けて変化する。

例

たとえば、関数 y＝x は、定義域をもし x ≧ 1 とした場合、

関数 y＝x の値域は y ≧ 1 となる。

また、この例のように、定義域や値域を表す場合に、不等式で表す手法も多い。

例2

たとえば、関数 y＝2x は、定義域をもし 1 ≦ x ≦ 3 とした場合、

関数 y＝2x の値域は 2 ≦ y ≦ 6 となる。

略式の記法として、定義域を表す場合に、

y＝2x 　　 ( 1 ≦ x ≦ 3 )

のようにカッコ内の不等式で表すことも、よくある。この記法（「 y＝2x 　　 ( 1 ≦ x ≦ 3 ) 」）の場合、定義域は 1 ≦ x ≦ 3 であると主張している。

つまり、定義域を数式ではっきりと示す必要がある場合には

$y=f(x)\qquad (a\leqq x\leqq b)$

のように示すことがよくある。この関数の場合、定義域は$a\leqq x\leqq b$である。

特に定義域の指定されてない場合は、可能なかぎり定義域を広くとるのが普通である。

たとえば、特に定義域が指定されていない場合、 関数 $y=x$ の定義域は、実数全体である。

関数 $y={\frac {1}{x}}$ の定義域には、 x＝0 を含めることはできない。そのため、特に定義域が指定されていない場合、 関数 $y={\frac {1}{x}}$ の定義域は、0をのぞく実数全体である。

その他の例

たとえば、関数 y＝-x＋5 は、定義域をもし 1 ≦ x ≦ 8 とした場合、

値域は -3 ≦ y ≦ 4 となる。

最大値と最小値

たとえば、さきほどの関数 y＝2x の問題の例 、

例 （再掲）

たとえば、関数 y＝2x は、定義域をもし 1 ≦ x ≦ 3 とした場合、

関数 y＝2x の値域は 2 ≦ y ≦ 6 となる。

では、与えられた定義域で、この関数の値のとりうる最大の値は 6 である。

このように、ある関数が、与えられた条件下でもつ最大の値のことを、その関数の最大値（さいだいち, maximum）という。

または、さきほど習った「値域」という言葉をつかうなら、「最大値」とは、値域の最大の値のことである。

つまり、関数 y＝2x 　　 ( 1 ≦ x ≦ 3 ) の最大値は 6 である。

もし、定義域を指定しなければ、関数 y＝2x に最大値は無い（定義域の指定がなければ、xが どこまでも大きくなるし、それに比例してyも大きくなるので）。

同様に、ある関数が、与えられた条件下でもつ最小の値のことを、その関数の最小値（さいしょうち, minimum）という。

関数 y＝2x 　　 ( 1 ≦ x ≦ 3 ) の最小値は 2 である。

例1

関数 y＝-x＋5 　　（ 1 ≦ x ≦ 8 ）では、

値域は -3 ≦ y ≦ 4 なので、

最大値は 4 , 最小値は -3 である。

例2

y＝2x 　　 ( 1 ＜ x ≦ 3 )では、（※ 不等号が「≦」ではなく「＜」になっているのに注意！）

値域は 2 ＜ y ≦ 6 であるが、

最小値は無い。xを1に近づけていくことで、yは2に近づいていくが、しかしxが1になることがないので、よってyが2になることもないので、この問題ではyに最小値は無い。

この問題でのyの最大値は6である。

2次関数の値の変化

2次関数の最大値・最小値

図1 (y=x²のグラフ)

定義域が実数全体である2次関数$y=ax^{2}+bx+c$ では、右図のように、aの正負によって最小値（a>0 の場合）、または最大値がある（a<0の場合）。

例1 　　関数 $y=x^{2}$ 　の場合

関数 $y=x^{2}$ では、すべての実数 $x$ に対して、$x^{2}\geqq 0$ であるので（ 等号成立は$x=0$のときのみ）、

よって、関数 $y=x^{2}$ は$x=0$のとき最小値0をとる。 関数 $y=x^{2}$ に最大値は存在しない。

例2　　関数 y＝2(x-3)²＋4　の場合

たとえば、実数の範囲で考えた場合、関数 y＝2(x-3)²＋4　の最小値は4である。

関数 y＝2(x-3)²＋4　 に最大値は無い。

例3　　関数 y＝-x² 　の場合

x² の係数がマイナスなので、最大値をもつ。最小値はもたない。

実数の範囲で考えた場合、関数 y＝x² の最大値は 0 である。

関数 y＝-x² に最小値は無い。

例題

例題

2次関数$y=x^{2}+5x+5$の$-3\leq x\leq 0$ の範囲での最大値・最小値を求めよ。

解

図2

$y=\left(x+{\frac {5}{2}}\right)^{2}-{\frac {5}{4}}$

と標準形にし、グラフを書くと右図のようになる。

したがってグラフより答えは最大値は$x=0$ のとき$5$, 最小値は$x=-{\frac {5}{2}}$ のとき$-{\frac {5}{4}}$。

例題

2次関数$y=-{\frac {1}{2}}x^{2}+x+{\frac {3}{2}}$ の$0\leq x<3$ の範囲での最大値・最小値を求めよ。

解

図3

上の例題と同様の問題のように思えるが、定義域が$0\leq x\leq 3$ ではなく、$0\leq x<3$ となっている。とりあえずグラフをかいてみることにする。

$y=-{\frac {1}{2}}(x-1)^{2}+2$.

グラフから、最大値は$x=1$ のとき$2$, 最小値は存在しない。

二次不等式

二次不等式とは、$x$ の二次式と不等号で表される式のことをいい、

$ax^{2}+bx+c>0$, $ax^{2}+bx+c\geq 0$

のような形をしている。グラフを利用して二次不等式の解を考えてみよう。

例題

図4

二次不等式 $x^{2}+4x>0$ を解け。

2次関数 $y=x^{2}+4x=x(x+4)$ のグラフは右図のようになる。

$x^{2}+4x>0$ となる$x$ の値の範囲は右のグラフの$x$ 軸より上側にある部分に対する$x$ の値の範囲であるから、

$x<-4,0<x$.

この問題をより一般化してみよう。 2次不等式$ax^{2}+bx+c>0$ を解くには$y=ax^{2}+bx+c$ のグラフをかけば一目瞭然である。しかし、グラフをかいた場合にも我々が注目するのは$x$ 軸より上か下かということと、$x$ 軸との共有点である。$x$ 軸との共有点は二次方程式$ax^{2}+bx+c=0$ の解であるが、二次方程式の解の公式を思い出してほしい。それは次のようなものであった。

二次方程式$ax^{2}+bx+c=0$が解を持つとき、その解$x$ は、

$x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}$

これを用いると、二次方程式$ax^{2}+bx+c=0$が解を持つとき、

$ax^{2}+bx+c=a\left(x-{\frac {-b+{\sqrt {b^{2}-4ac}}}{2a}}\right)\left(x-{\frac {-b-{\sqrt {b^{2}-4ac}}}{2a}}\right)$

と因数分解形で表すことができる。（右辺を展開して左辺と一致することを確かめてみよ。） ここで、

$\alpha ={\frac {-b-{\sqrt {b^{2}-4ac}}}{2a}},\beta ={\frac {-b+{\sqrt {b^{2}-4ac}}}{2a}}$

とおくと、

$ax^{2}+bx+c>0\Longleftrightarrow a(x-\alpha )(x-\beta )>0$

となる。$a>0$ のとき$y=ax^{2}+bx+c$ のグラフは下に凸であるからこの不等式の解は、

$x<\alpha ,\beta <x$

となる。$a<0$ のときは両辺を$-1$ で割ってから考えると、

$\alpha <x<\beta$

となる。

2次関数のグラフがx軸と異なる2点で交わる場合

• 例題

• • 問題

次の二次不等式を解け。
(i)

$12x^{2}+17x-7<0$

(ii)

$2x^{2}+6x+1\geq 0$

• • 解答

(i)　二次方程式$12x^{2}+17x-7=0$を解くと

$(4x+7)(3x-1)=0$

$x=-{\frac {7}{4}}\ ,\ {\frac {1}{3}}$

よって、この二次不等式の解は

$-{\frac {7}{4}}<x<{\frac {1}{3}}$

(ii)　二次方程式$2x^{2}+6x+1=0$を解くと

$x={\frac {-6\pm {\sqrt {6^{2}-4\times 2\times 1}}}{2\times 2}}={\frac {-6\pm {\sqrt {28}}}{4}}={\frac {-6\pm 2{\sqrt {7}}}{4}}={\frac {-3\pm {\sqrt {7}}}{2}}$

よって、この二次不等式の解は

${\frac {-3-{\sqrt {7}}}{2}}\leq x\ ,\ x\leq {\frac {-3+{\sqrt {7}}}{2}}$

2次関数のグラフがx軸と接する場合

$y=x^{2}-6x+9$の値の符号について考えよう。
平方完成をすると

$y=(x-3)^{2}$

この関数のグラフは、$x$軸と点$(3\ ,\ 0)$で接する。
$y=x^{2}-6x+9$の値の符号について、下の表のようになる。

$x$	$x<3$	$3$	$3<x$
$y=x^{2}-6x+9$	$+$	$0$	$+$

よって

$x^{2}-6x+9>0$の解は　3以外のすべての実数

$x^{2}-6x+9<0$の解は　ない

$x^{2}-6x+9\geq 0$の解は　すべての実数

$x^{2}-6x+9\leq 0$の解は　$x=3$

例題

• • 問題

次の二次不等式を解け。
(i)

$x^{2}+2x+1>0$

(ii)

$9x^{2}+12x+4\leq 0$

(iii)

$4x^{2}-4x+1<0$

(iv)

$x^{2}-10x+25\geq 0$

• • 解答

(i)

$x^{2}+2x+1>0$

$(x+1)^{2}>0$

よって、-1以外のすべての実数
(ii)

$9x^{2}+12x+4\leq 0$

$(3x+2)^{2}\leq 0$

よって、$x=-{\frac {2}{3}}$
(iii)

$4x^{2}-4x+1<0$

$(2x-1)^{2}<0$

よって、解はない
(iv)

$x^{2}-10x+25\geq 0$

$(x-5)^{2}\geq 0$

よって、すべての実数

2次関数のグラフがx軸と共有点をもたない場合

2次関数$y=ax^{2}+bx+c$のグラフと$x$軸の位置関係について、$D=b^{2}-4ac<0$のとき、$x$軸と共有点をもたなかった。
さらに$a>0$という条件を加えると、$y=ax^{2}+bx+c$のグラフは$x$軸より上側にある。

$a>0\ ,\ D=b^{2}-4ac<0$のとき

$ax^{2}+bx+c>0$の解は　すべての実数

$ax^{2}+bx+c<0$の解は　ない

例題

• • 問題

次の二次不等式を解け。
(i)

$x^{2}+2x+3<0$

(ii)

$2x^{2}-6x+5\geq 0$

(iii)

$-x^{2}+x-1\geq 0$

• • 解答

(i)

$x^{2}+2x+3<0$

$D=2^{2}-4\times 1\times 3=-8<0$

よって、解はない
(ii)

$2x^{2}-6x+5\geq 0$

$D=(-6)^{2}-4\times 2\times 5=-4<0$

よって、すべての実数
(iii)

$-x^{2}+x-1\geq 0$

$x^{2}-x+1\leq 0$

$D=(-1)^{2}-4\times 1\times 1=-3<0$

よって、解はない

（発展）放物線と直線

放物線と直線の共有点について考えよう。

• 問題例

• • 問題

放物線 $y=x^{2}-4x+5$ と次の直線の共有点の座標を求めよ。
(i)

$y=x+1$

(ii)

$y=2x-4$

• • 解答

(i)　求める共有点の座標は、連立方程式

${\begin{cases}y=x^{2}-4x+5\\y=x+1\end{cases}}$

の実数の解である。$y=x+1$ を $y=x^{2}-4x+5$ に代入すると

$x^{2}-4x+5=x+1$

すなわち

$x^{2}-5x+4=0$

これを解いて

$x=1\ ,\ 4$

$x=1$ のとき $y=2$
$x=4$ のとき $y=5$
よって、共有点の座標は

$\left(1\ ,\ 2\right)\ ,\ \left(4\ ,\ 5\right)$

である。
(ii)　求める共有点の座標は、連立方程式

${\begin{cases}y=x^{2}-4x+5\\y=2x-4\end{cases}}$

の実数の解である。$y=2x-4$ を $y=x^{2}-4x+5$ に代入すると

$x^{2}-4x+5=2x-4$

すなわち

$x^{2}-6x+9=0$

これを解いて

$x=3$

このとき $y=2$
よって、共有点の座標は

$\left(3\ ,\ 2\right)$

である。

例題の(ii)のように、放物線とその軸に平行でない直線がただ1点を共有するとき、放物線は直線に接するといい、共有点を接点という。

演習問題

• 演習問題A
• 演習問題B