ここでは三角関数の定義をしたあと、三角関数の基本的な性質、加法定理、三角関数の応用について学ぶ。三角関数は波やベクトルの内積、フーリエ変換などさまざまな分野で応用されている。


右図のように、定点Oを中心として回転する半直線 OP を考える。このときの回転する半直線 OP のことを動径という。
半直線 OX を角度の基準とする。この基準となる半直線 OX のことを始線という。
動径が時計回りに回転した場合、回転した角度は負であるとし、動径が反時計回りをした場合、回転した角度は正であるとする。
負の角度や360°以上回転する角度も考えに入れた角のことを一般角という。
いままでは角度の単位として一周を 360° とする度数法を使ってきたことだろう。ここで、弧度法による角度の表し方を学ぶ。

半径1 の扇形において弧の長さが 1 のときの中心角を 1 rad、同様に弧の長さがθのときの中心角をθ radと定義する。この定義より 180° =π rad、360° = 2π rad 、さらに

となる。また弧度法の単位(rad)はしばしば省略される。
弧度法を用いると、三角関数の微積分を考える際に便利である。(このことは数学IIIで学ぶ)
扇形の半径をr 、弧度法で定義された角度をθとするとき、弧の長さl と面積S は

と表せる。

一般角が  の半直線と単位円が交わる円を
の半直線と単位円が交わる円を  とする。このときの
とする。このときの  の座標を
の座標を とすることで、関数
とすることで、関数  を定める。また、
を定める。また、 とすることで関数
とすることで関数  を定める。
を定める。 は一般角が
は一般角が  の動径の傾きに等しい。
の動径の傾きに等しい。
 はサイン(sine) と発音され、正弦とも呼ばれる。
はサイン(sine) と発音され、正弦とも呼ばれる。 コサイン(cosine) と発音され、余弦とも呼ばれる。
コサイン(cosine) と発音され、余弦とも呼ばれる。 はタンジェント(tangent) と発音され、正接とも呼ばれる。
はタンジェント(tangent) と発音され、正接とも呼ばれる。
また、三角関数の累乗は  と表記される。
と表記される。
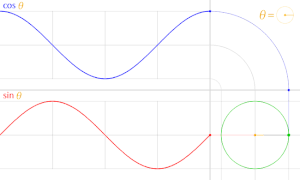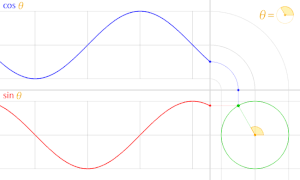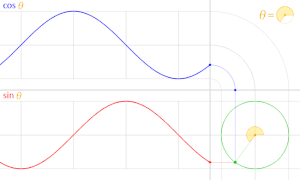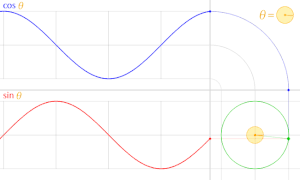

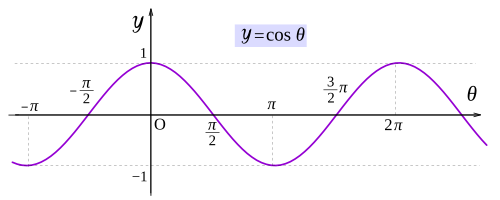
cos θ のグラフは sin θ のグラフを θ軸方向に  だけ平行移動したものである。
だけ平行移動したものである。
 や
や  の形をした曲線のことを 正弦曲線 (せいげんきょくせん)という。
の形をした曲線のことを 正弦曲線 (せいげんきょくせん)という。
関数  の値域はどちらも、
の値域はどちらも、![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01) である。
である。

右図のように 、角 θ の動径と単位円との交点をPとして、
直線OPと 直線x=1 との交点を T とすると、
Tの座標は
- T (1, tan θ)
になる。
このことを利用して、 y=tan θ のグラフをかくことができる。
y=tan θ のグラフは、下図のようになる。

y=tan θ のグラフでは、θの値が  に近づいていくと、
直線
に近づいていくと、
直線  に限りなく近づいていく。
に限りなく近づいていく。
このように、曲線がある直線に限り無く近づいていくとき、近づかれる直線のほうを 漸近線 (ぜんきんせん)という。
同様に考え、次の直線も y=tanθ の漸近線である。

は y=tanθ の漸近線である。
一般に、
- 直線
 (nは整数)
(nは整数)
はy=tanθのグラフの漸近線である。[1]
一般角が  の動径は一回転しても等しいので、一般角が
の動径は一回転しても等しいので、一般角が  の動径と等しい。これより三角関数の周期性
の動径と等しい。これより三角関数の周期性

を得る。
点  を
を  回転した点
回転した点  は原点を中心に点対称移動した点
は原点を中心に点対称移動した点  であることから
であることから

を得る。
点  を
を  軸で線対称移動移動した点が
軸で線対称移動移動した点が  であることから
であることから

を得る。
- 問題例
- ::

- を計算せよ。
- 角θに対応する点を P(x, y) とする。このとき、角 θ + 90°に対応する点を P'(x', y') とすると、この点の座標は、P'(-y, x) に対応する。このことから、P'について sin, cos を計算すると、

- が得られる。
- 同様にして、90°- θ に対応する点を P' '(x' ', y' ') とすると、

- となる。よって、

- が得られる。
単位円周上の点  から原点までの距離は 1 なので、
から原点までの距離は 1 なので、  が成り立つ。
が成り立つ。
また、この式に、  つまり、
つまり、  を代入すれば、
を代入すれば、 が成り立つことがわかる。
が成り立つことがわかる。
関数  に対して、0 でない実数
に対して、0 でない実数  が存在して、
が存在して、 となるとき関数
となるとき関数  は周期関数という。実数
は周期関数という。実数  が上の性質を満たすとき、
が上の性質を満たすとき、 など、実数
など、実数  を0を除く整数倍した数も上の性質を満たす。そこで、周期関数を特徴づける量として、上の性質を満たす実数
を0を除く整数倍した数も上の性質を満たす。そこで、周期関数を特徴づける量として、上の性質を満たす実数  の内、正でかつ最小のものを選び、これを周期と呼ぶ。
の内、正でかつ最小のものを選び、これを周期と呼ぶ。
 は周期を
は周期を  とする周期関数であり、
とする周期関数であり、 は周期を
は周期を  とする周期関数である。
とする周期関数である。
演習問題
 を0でない実数とする。関数
を0でない実数とする。関数  の周期を言え
の周期を言え
解答
 なので答えは
なので答えは  。これは正であり、周期の最小性の条件を満たしている。
。これは正であり、周期の最小性の条件を満たしている。
関数  が
が  を満たすとき、関数
を満たすとき、関数  は偶関数という。偶関数は
は偶関数という。偶関数は  軸に関して対称なグラフになる。
軸に関して対称なグラフになる。
また、関数  が
が  を満たすとき、関数
を満たすとき、関数  は奇関数という。偶関数は原点に関して対象なグラフになる。
は奇関数という。偶関数は原点に関して対象なグラフになる。
関数  (
( は整数)は偶関数となる。
は整数)は偶関数となる。
関数  (
( は整数)は奇関数となる。
は整数)は奇関数となる。
- 演習問題
 は偶関数かそれとも奇関数か調べよ。
は偶関数かそれとも奇関数か調べよ。
解答

なので、  は奇関数である。[2]
は奇関数である。[2]

関数  のグラフは、
のグラフは、 のグラフを θ軸方向に
のグラフを θ軸方向に  だけ平行移動させたものになり、周期は
だけ平行移動させたものになり、周期は  である。(平行移動しても、周期は変わらず、sinθと同じく周期は
である。(平行移動しても、周期は変わらず、sinθと同じく周期は  のままである。)
のままである。)

関数 y=2sin θ のグラフの形は y=sin θ をy軸方向に2倍に拡大したもので、周期は y=sin θ と同じく 2π である。
ー1 ≦ sin θ ≦ 1 なので、
値域は ー2 ≦ 2sin θ ≦ 2 である。

関数 y=sin2θ のグラフはy軸を基準にθ軸方向に  倍に縮小したものになっている。
倍に縮小したものになっている。
したがって、周期も  倍になっており、y=sinθ の周期は
倍になっており、y=sinθ の周期は  だから、y=sin2θ の周期は
だから、y=sin2θ の周期は  である。
である。
三角関数の加法定理

が成り立つ。
証明
任意の実数  に対し、単位円周上の点
に対し、単位円周上の点  をとる。このとき、 線分
をとる。このとき、 線分  の長さの2乗
の長さの2乗  は余弦定理を使うことにより
は余弦定理を使うことにより

である。次に三平方の定理を使って

これを整理して

を得る。

である。
以上をまとめて

を得る。
ここで、
 [3]
[3]
さらに、 についても
についても

が成り立つ。
加法定理を用いて以下の2倍角の公式が証明できる。



次に、  の2倍角の公式を変形すると
の2倍角の公式を変形すると


である。
ここで を
を に置き換えると、
に置き換えると、


である。(半角の公式)
この式は どちらの形でも多用する。
どちらの形でも多用する。
演習問題
 を求めよ
を求めよ を示せ
を示せ
解答



今までの定理をまとめると、次のようになる。
| 三角関数の加法定理
|

|
| 2倍角の公式
|

|
| 半角の公式
|

|
覚え方
加法定理は「咲いたコスモスコスモス咲いた」、「コスモスコスモス咲いた咲いた」という語呂合せがあります。
 の倍角の公式
の倍角の公式  は
は  という形を覚えて
という形を覚えて  は符号が
は符号が  、1 の符号はその逆と覚えます。
、1 の符号はその逆と覚えます。
半角の公式 は、
は、 という形を覚えて、
という形を覚えて、  は符号が
は符号が と考えます。
と考えます。
三角関数の和

において、 のとき
のとき
 なので、点
なので、点  は単位円周上の点であり、
は単位円周上の点であり、

となるようなαをとることができ、このαを用いて次のような変形ができる。

この式はサイン(正弦関数)に合成するので正弦合成と呼ぶ場合がある。
これに対し、コサイン(余弦関数)に合成する場合は余弦合成と呼ばれる。
合成は加法定理の逆の操作である。
演習問題
 は
は  を満たすとする。
を満たすとする。
 を
を  の形に変形せよ。
の形に変形せよ。 を
を  の形に変形せよ。
の形に変形せよ。
解答
 より
より

 [4]ここで、
[4]ここで、 である。
である。  となる
となる  として
として  がある。[5]したがって、
がある。[5]したがって、
 の合成の計算を簡略化するやり方として、以下のようなものが知られている。
の合成の計算を簡略化するやり方として、以下のようなものが知られている。
- 正弦合成の場合
- xy平面上に点
 をとる。
をとる。
- x軸の正の部分に始線をとり、OPを動径とみた時の回転角を
 とおく。
とおく。
- 三角方程式
 を解いて
を解いて の値を求める。
の値を求める。
- 求める式は
 である。
である。
- 余弦合成の場合
- xy平面上に点
 をとる。
をとる。
- x軸の正の部分に始線をとり、OQを動径とみた時の回転角を
 とおく。
とおく。
- 三角方程式
 を解いて
を解いて の値を求める。
の値を求める。
- 求める式は
 である。
である。
三角関数の加法定理を用いると、三角関数の和→積の公式、および積→和の公式が得られる。それぞれ
- 積→和の公式

- 和→積の公式

となる。
- 導出
加法定理

(1)

(2)

(3)

(4)
から、 (1) + (2) より

(1) - (2) より

(3) + (4) より

(3) - (4) より

が得られる。
 とおくと、
とおくと、  である。これを積→和の公式に代入すれば、それぞれ
である。これを積→和の公式に代入すれば、それぞれ

が得られる。
覚え方
積→和の公式は、上2つは  と
と  を入れ替えれば同じ式なので、覚えるのは3式でいい。
を入れ替えれば同じ式なので、覚えるのは3式でいい。 の公式は
の公式は  の公式の符号を2つ
の公式の符号を2つ  にしたものになっている。
にしたものになっている。
和→積の公式は、 の式は
の式は  の公式の
の公式の  と
と  を逆にした形になっている。
を逆にした形になっている。
- 問題
 を示せ。
を示せ。
- (右辺)

 2倍角・半角の公式
2倍角・半角の公式
 和→積の公式
和→積の公式

- (右辺)










 (補角の公式)
(補角の公式)



 (余角の公式)
(余角の公式)

- 問題例
- (i)

- (ii)

- (iii)

- の値を求めよ。
- (i)

- (ii)

- (iii)

楽器の音と三角関数
音も波の一種なので、三角関数で表現できる。
オシロスコープで 音叉 の音を測定すると、正弦波に近い波形が観測される。
しかし、実際の楽器の音は、正弦波とは違う。オシロスコープでギターやバイオリンなどの楽器の音を測定すると、正弦波でない波形が繰り返されている。
これら実際の楽器の音の波形は、周期の異なる複数個の正弦波を重ね合わせた波形になっている。
- 大学などで習うフーリエ解析で、このような正弦波でない波形の解析について詳しく習う。三角関数以外の周期的な関数を、三角関数を介して表現する手法が知られている。
(1)下の度数法で表された値を弧度法で表せ
1) 2)
2)
(2) の値を求めよ
の値を求めよ
(3) のグラフをかけ。
のグラフをかけ。
(4)以下を示せ。
1)
2)
(5) を
を の形で表せ。
の形で表せ。
(6) が成立するように
が成立するように を定めよ。
を定めよ。
(7)以下の式について、和の形であれば積の形に、積の形であれば和の形に変形せよ。
1)
2)
(8) とする。
とする。
1) としたとき、
としたとき、 を
を の式で表せ。
の式で表せ。
2) の範囲を求めよ。
の範囲を求めよ。
3) の最大値・最小値を求めよ。
の最大値・最小値を求めよ。
- ^ 高校・大学入試では使われないが、
 として定義される三角関数を使うところもある。これらの関数はそれぞれ、セカント、コセカント、コタンジェントと呼ばれる。
として定義される三角関数を使うところもある。これらの関数はそれぞれ、セカント、コセカント、コタンジェントと呼ばれる。
- ^ 一般に、関数
 に対し、
に対し、 が偶関数か奇関数か調べるには
が偶関数か奇関数か調べるには  が
が  または
または  のどちらに等しいか調べればよい。また、どちらとも等しくない場合、関数
のどちらに等しいか調べればよい。また、どちらとも等しくない場合、関数  は偶関数でも奇関数でもない。
は偶関数でも奇関数でもない。
- ^ 「咲いた(sin)コスモス(cos)コスモス(cos)咲いた(sin)」「コスモス(cos)コスモス(cos)咲いた(sin)咲いた(sin)」という覚えかたがある
- ^ こう変形することで、点
 が単位円周上の点になる
が単位円周上の点になる
- ^ ここで、
 は問題文の制約を満たすように選ぶ。
は問題文の制約を満たすように選ぶ。  に
に  の整数倍を足した
の整数倍を足した  を選んでも三角関数の合成はできるが、実用的にも
を選んでも三角関数の合成はできるが、実用的にも  は簡単なものを選んだ方がいいだろう。
は簡単なものを選んだ方がいいだろう。



























![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)






















































































































































































