高等学校数学II/指数関数・対数関数

高等学校の学習 > 高等学校数学 > 高等学校数学II > 高等学校数学II/指数関数・対数関数

指数の拡張

指数法則については、数学Iで すでに学んだ。

累乗根

a が実数のときで、n が2以上の正の整数のとき、 n 乗して a になる数、すなわち

$x^{n}=a$

となるx のことを、a の n 乗根という。a の2乗根、3乗根、4乗根、......を総称して、a の累乗根という。

平方根は2乗根である。なお、3乗根のことを立方根（りっぽうこん）ともいう。

この章の学習では、最終的に n を正の整数だけでなく、実数にまで拡張していくが、とりあえず学習当初の当面は n を整数で考えておこう。

例

2の4乗は16である。-2の4乗も16である。よって、16の4乗根は 2 と -2 である。

単に「n乗根」といった場合、係数に負の数がつくものを除外しないことに注意。

さて、nが奇数の場合のn乗根について、考えてみる。

（-2）を3乗しても、8にはならず、-2 の3乗は -8である。

（-3）を3乗しても、27にはならず、-3 の3乗は -27である。

このように、負の実数の奇数n乗は、かならず、負の数になる。

なので、8の3乗根には、負の数は ふくまれず、8の3乗根は 2だけである。

同様に、27の3乗根は、正の3だけである。

このように、nを奇数の自然数としたとき、実数 a のn乗根 は1通りである。

• 例

(I) 　2³ = 8 であるから、8の3乗根は2。

(II) 　3⁴ = (-3)⁴ = 81 であるから、81の4乗根は ± 3。

a のn 乗根 x について考える。

(1) 　n が奇数のとき、実数 a のn乗根 はただ1つであり、これを ${\sqrt[{n}]{a}}$ で表す。

• 例

${\sqrt[{3}]{8}}=2$

${\sqrt[{3}]{-8}}=-2$

${\sqrt[{5}]{-32}}=-2$

(2) 　n が偶数のとき、正の実数aのn乗根は、正と負の2つの数がある。

負のほうは $-{\sqrt[{n}]{a}}$ で表す。正の方は ${\sqrt[{n}]{a}}$、で表す。

a < 0 のとき、実数の範囲では a のn 乗根はない。

n が偶数か奇数かにかかわらず、0のn乗根は0なので、

${\sqrt[{n}]{0}}=0$

である。

• 例

(I) 　x⁴ = 3 であるとき、$x=\pm {\sqrt[{4}]{3}}$

(II) 　x⁶ = -16 を満たすx はない。

特に2乗根${\sqrt[{2}]{a}}$ は ${\sqrt {a}}$ と書く。

• 問題例
  • 問題

  次の値を求めよ。

  　(i) 　${\sqrt {36}}$

  　(ii) 　${\sqrt[{5}]{32}}$

  　(iii) 　${\sqrt[{3}]{-8}}$

  　(iv) 　$-{\sqrt[{4}]{81}}$

  • 解答

  　(i) 　${\sqrt {36}}={\sqrt {6^{2}}}=6$

  　(ii) 　${\sqrt[{5}]{32}}={\sqrt[{5}]{2^{5}}}=2$

  　(iii) 　${\sqrt[{3}]{-8}}={\sqrt[{3}]{(-2)^{3}}}=-2$

  　(iv) 　$-{\sqrt[{4}]{81}}=-{\sqrt[{4}]{3^{4}}}=-3$

累乗根の性質

a > 0 のとき、xⁿ = a の解は $x={\sqrt[{n}]{a}}$ であるから、

$\left({\sqrt[{n}]{a}}\right)^{n}=a$

また

${\sqrt[{n}]{a}}>0$

累乗根の公式

a > 0, b > 0 で、m, n, p が正の整数のとき 1 　${\sqrt[{n}]{a}}{\sqrt[{n}]{b}}={\sqrt[{n}]{ab}}$ 2 　${\frac {\sqrt[{n}]{a}}{\sqrt[{n}]{b}}}={\sqrt[{n}]{\frac {a}{b}}}$ 3 　$\left({\sqrt[{n}]{a}}\right)^{m}={\sqrt[{n}]{a^{m}}}$ 4 　${\sqrt[{m}]{\sqrt[{n}]{a}}}={\sqrt[{mn}]{a}}$ 5 　${\sqrt[{n}]{a^{m}}}={\sqrt[{np}]{a^{mp}}}$

例

${\sqrt {\sqrt[{3}]{729}}}={\sqrt[{2\times 3}]{729}}={\sqrt[{6}]{729}}={\sqrt[{6}]{3^{6}}}=3$

• 計算例

  (i) 　${\sqrt[{3}]{4^{2}}}={\sqrt[{3}]{2^{4}}}={\sqrt[{3}]{2^{3}\times 2}}=2{\sqrt[{3}]{2}}$

  (ii) 　${\sqrt[{3}]{4}}{\sqrt[{3}]{6}}={\sqrt[{3}]{4\times 6}}={\sqrt[{3}]{24}}={\sqrt[{3}]{2^{3}\times 3}}=2{\sqrt[{3}]{3}}$

  (iii) 　$\left({\sqrt[{4}]{9}}\right)^{3}={\sqrt[{4}]{9^{3}}}={\sqrt[{4}]{3^{6}}}={\sqrt[{2\times 2}]{3^{3\times 2}}}={\sqrt {3^{3}}}=3{\sqrt {3}}$

指数の拡張

有理数を指数とする場合

有理数を指数とする累乗を、次のように定義する。

有理数の指数

実数 a に対し、2つの正の整数mとnがあるとした場合、 $a^{\frac {m}{n}}={\sqrt[{n}]{a^{m}}}$ $a^{-{\frac {m}{n}}}={\frac {1}{\sqrt[{n}]{a^{m}}}}$

これは、指数が有理数の場合にも、指数法則が成り立つように定義したのである。実際、次が成り立つ。

指数法則

a > 0, b > 0 で、p, q が有理数のとき 　$a^{m}a^{n}=a^{m+n}$ 　$(a^{p})^{q}=a^{pq}$ 　$(ab)^{p}=a^{p}b^{p}$ 　${\frac {a^{r}}{a^{s}}}=a^{r-s}$ 　$\left({\frac {a}{b}}\right)^{r}={\frac {a^{r}}{b^{r}}}$

たとえば、x^1/3 は、3乗すると x¹ = x に等しいので、x の3乗根 ${\sqrt[{3}]{x}}$に等しい。

また、x⁰ については

${\begin{aligned}x^{0}&=x^{1-1}\\&=x\cdot x^{-1}\\&={\frac {x}{x}}\\&=1\end{aligned}}$

と考えることが出来る。よって、0以外の全ての実数x に対して、

$x^{0}=1$

が成り立つ。

• 問題例
  • 問題

  それぞれの計算を行い、式を簡単化せよ。

  (i) $9^{1/6}$

  (ii) $8^{1/3}$

  (iii) $48^{1/4}$

  (iv) $3^{1/3}\cdot 9^{1/6}$

  (v) $4^{2}\cdot 3^{1/2}\cdot 12^{1/2}$

  (vi) $4^{1/3}\cdot 3^{3/4}\cdot 12^{1/6}$

  (vii) $4^{0}$

  • 解答

  (i) $3^{{1} \over {3}}$

  (ii) $2$

  (iii) $2\cdot 3^{1/4}$

  (iv) $3^{{2} \over {3}}$

  (v) $96$

  (vi) $2\cdot 3^{{11} \over {12}}$

  (vii) $1$

指数法則1に、r = 3, s = -3 を代入すれば

$a^{3}\times a^{-3}=a^{3+(-3)}=a^{0}=1$

ゆえに

$a^{-3}={\frac {1}{a^{3}}}$

指数法則2に、r = 2/3, s = 3 を代入すれば

$\left(a^{\frac {2}{3}}\right)^{3}=a^{{\frac {2}{3}}\times 3}=a^{2}$

となるから、a^2/3 は a² の3乗根ということになる。つまり、

$a^{\frac {2}{3}}={\sqrt[{3}]{a^{2}}}$

指数法則1に、r = -2/3, s = 2/3 を代入すれば

$a^{-{\frac {2}{3}}}\times a^{\frac {2}{3}}=a^{-{\frac {2}{3}}+{\frac {2}{3}}}=a^{0}=1$

ゆえに

$a^{-{\frac {2}{3}}}={\frac {1}{a^{\frac {2}{3}}}}$

指数の拡張

a > 0 で、m, n が正の整数のとき $a^{0}=1$ $a^{-n}={\frac {1}{a^{n}}}$ $a^{\frac {m}{n}}={\sqrt[{n}]{a^{m}}}=\left({\sqrt[{n}]{a}}\right)^{m}$ $a^{-{\frac {m}{n}}}={\frac {1}{a^{\frac {m}{n}}}}$

指数が無理数の場合

たとえば $3^{\sqrt {2}}$ の場合、 これは、 ${\sqrt {2}}=1.41421\cdots$ であるが、

$3^{1.4}$ , 　$3^{1.41}$ , 　$3^{1.414}$ , 　$3^{1.4142}$ , 　$3^{1.41421}$ , ・・・

を考えると、その項は一定値 4.72880 ・・・ に近づくので、その値を $3^{\sqrt {2}}$ と定める。

このようにして、累乗の指数が無理数の場合にも定義を拡張することで、指数を実数にまで拡張できる。また、実数の場合も上述の指数法則が成り立つ。

指数関数

指数関数のグラフ

実数aを a>0 で a≠1 とするとき、$y=a^{x}$ で表される関数のことを「 aを底（てい）とする指数関数」のようにいう。

※ 指数関数の底aには、1の場合をふくめない。なぜなら、1は何乗しても1のままなので、もし1を底とする指数関数のグラフを書いてもy＝1のグラフと同じになる。これは、数学的につまらない上に、他の底の指数関数とは大きく性質が異なり、例外扱いしなければならなくなる。ゆえに、ここではaに1をふくめないことにする。

さて、指数関数の例として、たとえば、

$y=2^{x}$

があげられる。

指数関数 $y=2^{x}$ のグラフを右に示す。指数関数はきわめて速く増加する関数であることが分かる。

次に $y=\left({\frac {1}{2}}\right)^{x}$ のグラフを書いてみよう。結果は、右のグラフの実線のようになる。

さきほどのグラフと比較すると分かるように、y軸を対称軸として、$y=\left({\frac {1}{2}}\right)^{x}$ のグラフと $y=2^{x}$ のグラフは対称になっている。

一般に、$y=\left({\frac {1}{a}}\right)^{x}$ のグラフは、y軸に関して $y=a^{x}$ のグラフと対称である。

また、

a＞1 のとき、グラフの形は右上がりである（ $y=2^{x}$と同様）。

いっぽう、

a＜1 のとき、グラフの形は右上がりである（ $y=\left({\frac {1}{2}}\right)^{x}$ と同様）。

なお、グラフの傾きをみれば分かるように、指数関数のグラフは、一次関数や二次関数のグラフと比べると、急激に増加または急激に減少していく。

• 問題

指数法則を用いて指数関数を簡単化せよ。

(i) 　$2^{x}\cdot 3^{x}$

(ii) 　$(1/3)^{x}$

解答

(i) 　指数法則3

$(a\cdot b)^{x}=a^{x}\cdot b^{x}$

を用いて、

$2^{x}\cdot 3^{x}=(2\cdot 3)^{x}=6^{x}$

となる。

(ii) 　1/3 = 3^-1 より、

$(1/3)^{x}=(3^{-1})^{x}=3^{-x}$

が得られる。

指数関数の性質

指数関数の値域は正の実数全体である。

また、どんな正の実数も、0乗すると1になるので、よって指数関数 $y=a^{x}$ のグラフは必ず点 (0,1) を通る。

対数関数

対数の定義

指数関数のグラフ（※ 対数関数のグラフではないので、混同しないように！）

a＞0,　a≠1 のとき、前章で習った指数関数のグラフの形からも分かるように、

任意の正の実数Mに対して、 $a^{p}=M$をみたす p はただ1つに定まる。

この p を $\log _{a}M$ と書き

aを底（てい）とするMの対数（たいすう）

という。 すなわち、

$a^{p}=M\quad \Leftrightarrow \quad p=\log _{a}M$

である。

なお、対数は英語で logarithm （ロガリスム）という。

指数と対数

a＞0 ,　a≠1 　の関係のとき、 M ＞ 0 のとき、 $a^{p}=M\quad \Leftrightarrow \quad p=\log _{a}M$

例

$\log _{2}8=3$

である。この場合、2 を log₂ 8 = 3 乗すると、8が得られるという関係になっている。

公式

$\log _{a}x$ について 以下の式が成り立つ。

1. 　$\log _{b}x^{a}=a\log _{b}x$
2. 　$\log _{a}a=1$
3. 　$\log _{x}1=0$

導出

1. $\log _{b}x^{a}=a\log _{b}x$

   の両辺について各々の式をb の指数として使ったものを計算する。

   まず log の定義にしたがうと、

   $b^{\log _{b}x^{a}}=x^{a}$

   がわかる。次に、右辺についても同じことを考えてみると

   $b^{a\log _{b}x}={(b^{\log _{b}x})}^{a}=(x)^{a}$

   となり、左辺を用いて計算した結果と一致する。よって

   $\log _{b}x^{a}=a\log _{b}x$

   が成立する。

2. 　2つ目の式について、a¹ = a であることを用いると、log_a a は確かに 1 である。
3. 　同様に x⁰ = 1 であることを用いると（これは x⁰ = x^1-1 = x /x = 1 であることから従う)、log_x 1 = 0 であることが分かる。

• 問題例
  • 問題

  それぞれの表式を簡単化せよ。

  (i) 　$\log _{2}9$

  (ii) 　$\log _{3}21$

  (iii) 　$\log _{5}125$

  (iv) 　$\log _{4}7$

  (v) 　$\log _{2}6$

  • 解答

  (i) 　9 = 3² を用いると、

  $\log _{2}9=2\log _{2}3$

  (ii)

  ${\begin{aligned}\log _{3}21&=\log _{3}(3\cdot 7)\\&=\log _{3}3+\log _{3}7\\&=1+\log _{3}7\end{aligned}}$

  (iii)

  $\log _{5}125=\log _{5}(5^{3})=3$

  (iv)

  $\log _{4}7=\log _{2^{2}}7={\frac {1}{2}}\log _{2}7$

  (v)

  ${\begin{aligned}\log _{2}6&=\log _{2}(2\times 3)\\&=\log _{2}2+\log _{2}3\\&=1+\log _{2}3\end{aligned}}$

  • 問題

  a = log₁₀ 2, b = log₁₀ 3 を用いて、

  (i) 　$\log _{10}6$

  (ii) 　$\log _{10}5$

  (iii) 　$\log _{10}25$

  (iv) 　$\log _{10}24$

  を計算せよ。

  • 解答

  (i)

  ${\begin{aligned}\log _{10}6&=\log _{10}(2\times 3)\\&=\log _{10}2+\log _{10}3\\&=a+b\end{aligned}}$

  (ii)

  ${\begin{aligned}\log _{10}5&=\log _{10}({\frac {10}{2}})\\&=\log _{10}10-\log _{10}2\\&=1-a\end{aligned}}$

  (iii)

  ${\begin{aligned}\log _{10}25&=\log _{10}(5^{2})\\&=2\log _{10}5\end{aligned}}$

  ここで、(ii)の結果を用いると、

  ${\begin{aligned}\log _{10}25&=2(1-a)\\&=2-2a\end{aligned}}$

  (iv)

  ${\begin{aligned}\log _{10}24&=\log _{10}(2^{3}\times 3)\\&=3\log _{10}2+\log _{10}3\\&=3a+b\end{aligned}}$

対数関数とそのグラフ

対数関数を、実数xに対し

$y=\log _{a}x$　　（a は1以外の正の実数）

を対応させる関数として定義する。

この関数の定義域（ていぎいき）は、x > 0 に限られる。これは、仮に

$\log _{a}x=l$

とすると、

$a^{l}=x$

となるが、 a が正の数であることからlがどのような値であろうと左辺は常に正であるから、xも正でなければならないからである。

グラフの概形を右に示す。図を見ると、この関数は非常にゆっくりと増大する関数であることが分かる。

更に、グラフの特徴として、

${\begin{aligned}\log _{a}a&=1,\\\log _{a}1&=0\end{aligned}}$

から、対数関数のグラフは、点 (1, 0) および 点 (a , 1) の2点を必ず通過することが分かる。

対数関数と指数関数

右図のように、対数関数のグラフは、対応する指数関数のグラフと y＝x に関して対称である。

一般に $y=\log _{a}x$ のグラフは $y=a^{x}$ のグラフと直線 y＝x に関して対称である。

• 問題例
  • 問題

  次の関数のグラフを描け。

  (i) 　$\log _{5}x$

  (ii) 　$\log _{1/10}x$

  (iii) 　$\log _{2}x^{2}$

  • 解答

  (i) 　2点 (x , y ) = (5, 1), (1, 0) を通りy軸が漸近線になることに注意してグラフを描けばよい。

  (ii)　

  $\log _{1/10}x=\log _{10^{-1}}x=-\log _{10}x$

  となる。したがって、2点 (x , y ) = (10, -1), (1, 0), (0, +∞) を通りy軸が漸近線になることに注意してグラフを描けばよい。

  (iii)　

  $\log _{2}x^{2}=2\log _{2}x$

  となる。(i)と同じようにグラフを描けばよい。

対数関数の性質

1. 　高校で習う範囲では、対数の定義域は正の実数全体、値域は実数全体である。
2. 　対数関数のグラフは点 (1, 0) および 点 (a , 1) の2点を通り、y軸が漸近線（ぜんきんせん）である。

対数の基本公式

指数法則と対数の定義とを組み合わせることにより、次の公式が導かれる。

1. 　$\log _{a}M+\log _{a}N=\log _{a}MN$
2. 　$\log _{a}M-\log _{a}N=\log _{a}{\frac {M}{N}}$
3. 　$\log _{a}M^{r}=r\log _{a}M$

証明

( 1. の証明)

$\log _{a}M=p$ ,　$\log _{a}N=q$ 　とおくと、 $M=a^{p}$ ,　$N=a^{q}$ 　であるから

$MN=a^{p}a^{q}=a^{p+q}$

よって 　　$\log _{a}MN=p+q=\log _{a}M+\log _{a}N$

( 2. 以降の証明)

※ ( 1.)の証明法と同様に右辺を指数に置きかえて計算したあとに再び対数に変形することで証明できる。（証明は省略）

追加の公式

上記の公式の特別な場合として、次の公式が成り立つ。

1. 　$\log _{a}{\frac {1}{N}}=-\log _{a}N$
2. 　$\log _{a}{\sqrt[{n}]{M}}={\frac {1}{n}}\log _{a}M$

その他

次の公式が成り立つ。

　$\log _{a}b={\frac {\log _{c}b}{\log _{c}a}}$

常用対数

10を底とする対数を常用対数（じょうよう たいすう）という。1.00から9.99までの値に対する常用対数の値は常用対数表に示してある。また、近年ではコンピュータや関数電卓を用いて、対応する対数の値を知ることもできる。ただし、これらの値は計算上の制約を受けるため、盲目的にその値が正しいと考えてはならない。コンピュータ内の計算については、高等学校情報などを参照。

• 問題例
  • 問題

  常用対数表を用いて、次の値を求めよ。

  (i) 　$\log _{10}12.2$

  (ii) 　$\log _{10}0.0143$

  (iii) 　$\log _{2}3$

  • 解答

  (i) 　$\log _{10}12.2=\log _{10}(1.22\times 10)=\log _{10}1.22+\log _{10}10=0.0864+1=1.0864$

  (ii) 　$\log _{10}0.0143=\log _{10}(1.43\times 10^{-2})=\log _{10}1.43+\log _{10}10^{-2}=0.1553-2=-1.8447$

  (iii) 　底の変換公式より $\log _{2}3={\frac {\log _{10}3}{\log _{10}2}}={\frac {0.4771}{0.3010}}=1.585\cdots$

235の桁数を常用対数を使って考えよう。

$10^{2}<235<10^{3}$

が成り立つ。各辺の常用対数をとると

$\log _{10}10^{2}<\log _{10}235<\log _{10}10^{3}$

すなわち

$2<\log _{10}235<3$

逆に、235が $2<\log _{10}235<3$ を満たすならば、上の計算を逆にたどって

$10^{2}<235<10^{3}$

よって、235は3桁の整数である。桁数が不明な大きな数に対して同様に常用対数をとることによって、おおよその大きさを知ることができる。

• 問題例
  • 問題

  　2³⁰ は何桁の整数か。ただし、log₁₀ 2 = 0.3010 とする。

  • 解答

  $\log _{10}2^{30}=30\log _{10}2=30\times 0.3010=9.03$

  ゆえに

  $9<\log _{10}2^{30}<10$

  よって

  $10^{9}<2^{30}<10^{10}$

  したがって、2³⁰ は10桁の整数である。

演習問題

1 $\log _{10}x$が実数とする。 上の式を満たすxが無限にあることを示せ

2 $x\leqq a\leqq b$ とする。このとき$R$を実数全体の集合とする。$a,b,x\in R$のとき$\log _{x}a=b$を満たすa,b,xが少なくとも1つはあることを示せ。 3 $\log _{a}{1+x}$のグラフを書け。

演習問題の解答と手引き

$\log _{10}x=q$と置く。 対数関数の定義より、$10^{q}=x$と書けるつまりxは x=100,10000,1000000•••のようになる。 (qが自然数であるとき) つまりxを無限に近づけることで命題は示された。

コラム

科学と対数

自然科学で用いられる数量のなかには、対数で表現されているものもある。

たとえば、星の等級（一等星や六等星など）は、指数で明るさの等級が決められており、 等級が1下がるごとに明るさが

$100^{\frac {1}{5}}=2.518\cdots$

倍となるように定められている。これは、等級とは明るさの対数だということである。

地震のエネルギーを表すマグニチュードも、指数によって定義されている。地震のエネルギーをEとし、マグニュチュードをMとすると、

$E/\mathrm {J} =10^{4.8+1.5M}$

となるようにマグニチュードが定められている。ここで、$E/{\rm {J}}$はエネルギーをジュール J 単位で表した数値である。 マグニチュード9.0の東北地方太平洋沖地震（東日本大震災）では、2.0 × 10¹⁸ J = 2.0 EJ のエネルギーが放出されたことになる。

このほか、音の大きさ（音圧レベル）をあらわすデシベルは、音圧（音の振幅） p に対して、最小可聴値の $p_{0}=20\ {\rm {\mu Pa}}$ を基準にして

$L_{p}/\mathrm {dB} =10\log _{10}{\frac {p^{2}}{{p_{0}}^{2}}}=20\log _{10}{\frac {p}{p_{0}}}$

で定義される。

同じ音圧レベルの音であっても、音の周波数によって聞こえやすさは異なる。1 kHz の純音の音圧レベルを基準にして、これと同じ大きさに聞こえる純音を結んだ曲線は等ラウドネス曲線と呼ばれる。

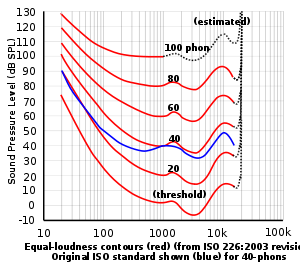等ラウドネス曲線。1 kHzの純音の音圧レベルdBと同じ大きさの音をphonという単位で表す。

フェヒナーの法則という心理学の法則は、人間の感じる感覚量 $E$ と物理的な刺激の強度 $R$ は対数の関係 $E=C\log R$ にある($C$ は定数)という主張である。このように、人間の感覚量について考えるときは、対数がよく登場する。星の等級も対数スケールであったし、音の高さも対数スケールで考えられる。平均律では、隣り合う音の周波数比が $2^{\frac {1}{12}}$ となるように、オクターブを12等分している。この12音で隣り合った音の間隔を半音、1音飛ばしにした音の間隔を全音という。ここで、12音の中から7音を

ド 全音 レ 全音 ミ 半音 ファ 全音 ソ 全音 ラ 全音 シ 半音 ド

となるように選ぶと全音階が得られる。なぜこのように音を選ぶかというと、$2^{\frac {7}{12}}\approx 1.498$ であって、これは3/2 にほぼ等しい。3/2のように単純な周波数比の和音は美しく感じる性質がある。そこで、7半音離れた音を集めて音階を作るのである。ドから始めて、7半音上の音を並べると、 ド ソ レ ラ ミ シ ファ＃ ド＃ ソ＃ レ＃ ラ＃ ファ ド となる。このように並べると、全音階は7半音だけ離れた音を7つ集めたものであるということがわかる。ちなみに、ここから ド ソ レ ラ ミ の五音を選ぶと、ヨナ抜き音階となる。このように、音楽と数学には密接な関係がある。

他にも、化学における水素イオン指数 pH も対数で定義される。

また、放射性年代測定も、残存している放射性同位体の量の対数を考えることにより可能になる。

一般に、非常に大きくなる量、または非常に小さくなる量をあらわすのに、対数を用いることが便利なのである。上記に紹介した、星の等級、地震のマグニチュード、音の大きさ、酸性度は、すべて、対数を使わないそのままでは桁が大きくなり扱いにくくなので、利便性のために対数を用いているということである。

対数方眼紙というのがあり、右図のようになっている。

片対数方眼紙