高等学校数学II/三角関数

高等学校の学習 > 高等学校数学 > 高等学校数学II > 高等学校数学II/三角関数

ここでは三角関数の定義をしたあと、三角関数の基本的な性質、加法定理、三角関数の応用について学ぶ。三角関数は波やベクトルの内積、フーリエ変換などさまざまな分野で応用されている。

角の拡張

一般角

右図のように、定点Oを中心として回転する半直線 OP を考える。このときの回転する半直線 OP のことを動径という。

半直線 OX を角度の基準とする。この基準となる半直線 OX のことを始線という。

動径が時計回りに回転した場合、回転した角度は負であるとし、動径が反時計回りをした場合、回転した角度は正であるとする。

負の角度や360°以上回転する角度も考えに入れた角のことを一般角という。

弧度法

ラジアン

いままでは角度の単位として一周を 360° とする度数法を使ってきたことだろう。ここで、弧度法による角度の表し方を学ぶ。

半径1 の扇形において弧の長さが 1 のときの中心角を 1 rad、同様に弧の長さがθのときの中心角をθ radと定義する。この定義より 180° =π rad、360° = 2π rad 、さらに

${\begin{aligned}1^{\circ }&={\frac {\pi }{180}}\,\mathrm {rad} \\\\1\,\mathrm {rad} &={\frac {180}{\pi }}^{\circ }\approx 57.3^{\circ }\end{aligned}}$

となる。また弧度法の単位（rad）はしばしば省略される。

弧度法を用いると、三角関数の微積分を考える際に便利である。（このことは数学IIIで学ぶ）

扇形の弧の長さと面積

扇形の半径をr 、弧度法で定義された角度をθとするとき、弧の長さl と面積S は

${\begin{aligned}l&=r\theta ,\\\\S&={\frac {1}{2}}r^{2}\theta ={\frac {1}{2}}rl\end{aligned}}$

と表せる。

三角関数

sin と cos のグラフ

一般角が $\theta$ の半直線と単位円が交わる円を $\mathrm {P}$ とする。このときの $\mathrm {P}$ の座標を$(\cos \theta ,\sin \theta )$ とすることで、関数 $\sin ,\cos$ を定める。また、$\tan \theta ={\frac {\sin \theta }{\cos \theta }}$ とすることで関数 $\tan \theta$ を定める。$\tan \theta$ は一般角が $\theta$ の動径の傾きに等しい。

• $\sin$ はサイン(sine) と発音され、正弦とも呼ばれる。
• $\cos$ コサイン(cosine) と発音され、余弦とも呼ばれる。
• $\tan$ はタンジェント(tangent) と発音され、正接とも呼ばれる。

また、三角関数の累乗は $(\sin \theta )^{n}=\sin ^{n}\theta$ と表記される。

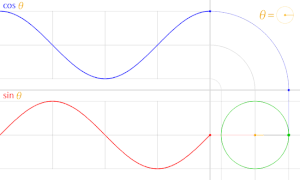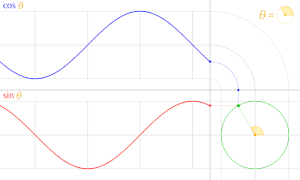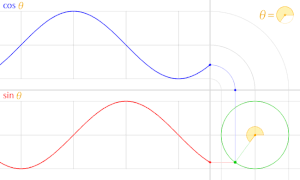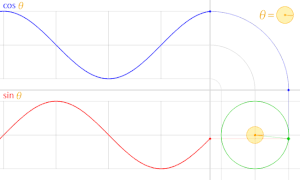
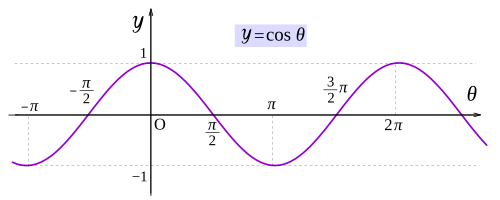
cos θ のグラフは sin θ のグラフを θ軸方向に $-{\frac {\pi }{2}}$だけ平行移動したものである。

$y=\sin \theta$ や $y=\cos \theta$ の形をした曲線のことを 正弦曲線 （せいげんきょくせん）という。

関数 $\sin ,\cos$ の値域はどちらも、$[-1,1]$ である。

tan のグラフ

右図のように 、角 θ の動径と単位円との交点をPとして、 直線OPと 直線x＝1 との交点を T とすると、 Tの座標は

T (1, tan θ)

になる。

このことを利用して、 y＝tan θ のグラフをかくことができる。

y=tan θ のグラフは、下図のようになる。

y=tan θ のグラフでは、θの値が ${\frac {\pi }{2}}$ に近づいていくと、 直線 $\theta ={\frac {\pi }{2}}$ に限りなく近づいていく。

このように、曲線がある直線に限り無く近づいていくとき、近づかれる直線のほうを 漸近線 （ぜんきんせん）という。

同様に考え、次の直線も y＝tanθ の漸近線である。

$\cdots ,\quad \theta =-{\frac {3}{2}}\pi ,\quad \theta =-{\frac {1}{2}}\pi ,\quad \theta ={\frac {1}{2}}\pi ,\quad {\frac {3}{2}}\pi ,\cdots$

は y＝tanθ の漸近線である。

一般に、

直線 $\quad \theta ={\frac {\pi }{2}}+n\pi$ 　　（nは整数）

はy=tanθのグラフの漸近線である。

三角関数の性質

一般角が $\theta$ の動径は一回転しても等しいので、一般角が $\theta +2\pi$ の動径と等しい。これより三角関数の周期性

${\begin{aligned}\sin(\theta +2\pi n)&=\sin \theta \\\cos(\theta +2\pi n)&=\cos \theta \\\tan(\theta +2\pi n)&=\tan \theta \end{aligned}}$

を得る。

点 $(\cos \theta ,\sin \theta )$ を $\pi$ 回転した点 $(\cos(\theta +\pi ),\sin(\theta +\pi ))$ は原点を中心に点対称移動した点　$(-\cos \theta ,-\sin \theta )$ であることから

${\begin{aligned}\sin(\theta +\pi )&=-\sin \theta \\\cos(\theta +\pi )&=-\cos \theta \\\tan(\theta +\pi )&=\tan \theta \end{aligned}}$

を得る。

点 $(\cos \theta ,\sin \theta )$ を $x$ 軸で線対称移動移動した点が $(\cos(-\theta ),\sin(-\theta ))=(\cos \theta ,-\sin \theta )$ であることから

${\begin{aligned}\sin(-\theta )&=-\sin \theta \\\cos(-\theta )&=\cos \theta \\\tan(-\theta )&=-\tan \theta \end{aligned}}$

を得る。

• 問題例
  • 問題
• ::${\begin{aligned}&\sin(\theta +{\frac {\pi }{2}})\\&\cos(\theta +{\frac {\pi }{2}})\\&\sin({\frac {\pi }{2}}-\theta )\\&\cos({\frac {\pi }{2}}-\theta )\end{aligned}}$

  を計算せよ。

  • 解答

  角θに対応する点を P(x, y) とする。このとき、角 θ + 90°に対応する点を P'(x', y') とすると、この点の座標は、P'(-y, x) に対応する。このことから、P'について sin, cos を計算すると、

  ${\begin{aligned}x'&=-y\\&=\cos(\theta +{\frac {\pi }{2}})\\&=-\sin \theta \\y'&=x\\&=\sin(\theta +{\frac {\pi }{2}})\\&=\cos \theta \end{aligned}}$

  が得られる。

  同様にして、90°- θ に対応する点を P' '(x' ', y' ') とすると、

  ${\begin{aligned}x''&=y\\y''&=x\end{aligned}}$

  となる。よって、

  ${\begin{aligned}\sin({\frac {\pi }{2}}-\theta )&=\cos \theta \\\cos({\frac {\pi }{2}}-\theta )&=\sin \theta \end{aligned}}$

  が得られる。

単位円周上の点 $(\cos \theta ,\sin \theta )$ から原点までの距離は 1 なので、 $\sin ^{2}\theta +\cos ^{2}\theta =1$ が成り立つ。

また、この式に、 $\tan \theta ={\frac {\sin \theta }{\cos \theta }}$ つまり、 $\sin \theta =\tan \theta \cos \theta$ を代入すれば、$1+\tan ^{2}\theta ={\frac {1}{\cos ^{2}\theta }}$ が成り立つことがわかる。

周期関数

関数 $f(x)$ に対して、0 でない実数 $p$ が存在して、$f(x+p)=f(x)$ となるとき関数 $f(x)$ は周期関数という。実数 $p$ が上の性質を満たすとき、$-p,2p$ など、実数 $p$ を0を除く整数倍した数も上の性質を満たす。そこで、周期関数を特徴づける量として、上の性質を満たす実数 $p$ の内、正でかつ最小のものを選び、これを周期と呼ぶ。

$\sin x,\cos x$ は周期を $2\pi$ とする周期関数であり、$\tan x$ は周期を $\pi$ とする周期関数である。

演習問題

$k$ を0でない実数とする。関数 $\sin kx$ の周期を言え

解答

$\sin k\left(x+{\frac {2\pi }{k}}\right)=\sin kx$ なので答えは ${\frac {2\pi }{k}}$ 。これは正であり、周期の最小性の条件を満たしている。

偶関数と奇関数

関数 $f(x)$ が $f(-x)=f(x)$ を満たすとき、関数 $f(x)$ は偶関数という。偶関数は $y$ 軸に関して対称なグラフになる。

また、関数 $f(x)$ が $f(-x)=-f(x)$ を満たすとき、関数 $f(x)$ は奇関数という。偶関数は原点に関して対象なグラフになる。

関数 $\cos \theta ,x^{2n}$ ($n$ は整数)は偶関数となる。

関数 $\sin x,x^{2n+1}$ ($n$ は整数)は奇関数となる。

演習問題

$\tan \theta$ は偶関数かそれとも奇関数か調べよ。

解答

$\tan(-\theta )={\frac {\sin(-\theta )}{\cos(-\theta )}}={\frac {-\sin(\theta )}{\cos(\theta )}}=-{\frac {\sin(\theta )}{\cos(\theta )}}=-\tan \theta$

なので、 $\tan \theta$ は奇関数である。

いろいろな三角関数

関数 $y=\sin \left(\theta -{\frac {\pi }{3}}\right)$ のグラフは、$y=\sin \theta$のグラフを θ軸方向に ${\frac {\pi }{3}}$ だけ平行移動させたものになり、周期は $2\pi$ である。（平行移動しても、周期は変わらず、sinθと同じく周期は $2\pi$ のままである。）

関数 y＝2sin θ のグラフの形は y＝sin θ をy軸方向に2倍に拡大したもので、周期は y＝sin θ と同じく 2π である。

ー1 ≦ sin θ ≦ 1　　なので、

値域は　　ー2 ≦ 2sin θ ≦ 2　　である。

関数 y＝sin2θ のグラフはy軸を基準にθ軸方向に ${\frac {1}{2}}$ 倍に縮小したものになっている。

したがって、周期も ${\frac {1}{2}}$ 倍になっており、y=sinθ の周期は $2\pi$ だから、y=sin2θ の周期は $\pi$ である。

加法定理

三角関数の加法定理

${\begin{aligned}\sin(\alpha \pm \beta )&=\sin \alpha \cos \beta \pm \cos \alpha \sin \beta \\\cos(\alpha \pm \beta )&=\cos \alpha \cos \beta \mp \sin \alpha \sin \beta \end{aligned}}$

が成り立つ。

証明

任意の実数 $\alpha ,\beta$ に対し、単位円周上の点 $\mathrm {A} (\cos \alpha ,\sin \alpha ),\mathrm {B} (\cos \beta ,\sin \beta )$ をとる。このとき、 線分 $\mathrm {AB}$ の長さの2乗 $\mathrm {AB} ^{2}$ は余弦定理を使うことにより

$\mathrm {AB} ^{2}=2-2\cos(\alpha -\beta )$

である。次に三平方の定理を使って

$\mathrm {AB} ^{2}=(\cos \alpha -\cos \alpha )^{2}+(\sin \alpha -\sin \beta )^{2}=2-2(\cos \alpha \cos \beta +\sin \alpha \sin \beta )$

これを整理して

$\cos(\alpha -\beta )=\cos \alpha \cos \beta +\sin \alpha \sin \beta$

を得る。

$\cos(\alpha +\beta )=\cos(\alpha -(-\beta ))=\cos \alpha \cos(-\beta )+\sin \alpha \sin(-\beta )=\cos \alpha \cos \beta -\sin \alpha \sin \beta$

である。

以上をまとめて

$\cos(\alpha \pm \beta )=\cos \alpha \cos \beta \mp \sin \alpha \sin \beta$

を得る。

ここで、

$\sin(\alpha \pm \beta )=-\cos(\alpha +{\frac {\pi }{2}}\pm \beta )=-\{\cos(\alpha +{\frac {\pi }{2}})\cos(\beta )\mp \sin(\alpha +{\frac {\pi }{2}})\sin \beta \}=\sin \alpha \cos \beta \pm \cos \alpha \sin \beta$

さらに、$\tan x$ についても

${\textstyle {\begin{aligned}\tan(\alpha \pm \beta )&={\frac {\sin(\alpha \pm \beta )}{\cos(\alpha \pm \beta )}}\\&={\frac {\sin \alpha \cos \beta \pm \cos \alpha \sin \beta }{\cos \alpha \cos \beta \mp \sin \alpha \sin \beta }}\\&={\cfrac {{\cfrac {\sin \alpha \cos \beta }{\cos \alpha \cos \beta }}\pm {\cfrac {\cos \alpha \sin \beta }{\cos \alpha \cos \beta }}}{{\cfrac {\cos \alpha \cos \beta }{\cos \alpha \cos \beta }}\mp {\cfrac {\sin \alpha \sin \beta }{\cos \alpha \cos \beta }}}}\\&={\frac {\tan \alpha \pm \tan \beta }{1\mp \tan \alpha \tan \beta }}\end{aligned}}}$

が成り立つ。

2倍角・半角の公式

加法定理を用いて以下の2倍角の公式が証明できる。

$\sin 2\alpha =\sin(\alpha +\alpha )=2\sin \alpha \cos \alpha$

$\cos 2\alpha =\cos(\alpha +\alpha )=\cos ^{2}\alpha -\sin ^{2}\alpha =2\cos ^{2}\alpha -1=1-2\sin ^{2}\alpha$

$\tan 2\alpha ={\frac {2\tan \alpha }{1-\tan ^{2}\alpha }}$

次に、 $\cos$ の2倍角の公式を変形すると

$\sin ^{2}\alpha ={\frac {1-\cos 2\alpha }{2}}$

$\cos ^{2}\alpha ={\frac {1+\cos 2\alpha }{2}}$

である。

ここで$\alpha$を${\frac {\alpha }{2}}$に置き換えると、

$\sin ^{2}{\frac {\alpha }{2}}={\frac {1-\cos \alpha }{2}}$

$\cos ^{2}{\frac {\alpha }{2}}={\frac {1+\cos \alpha }{2}}$

である。（半角の公式）

この式は${\frac {\alpha }{2}},\alpha$どちらの形でも多用する。

演習問題

1. $\sin 15^{\circ },\cos 15^{\circ }$ を求めよ
2. $\tan ^{2}\alpha ={\frac {1-\cos 2\alpha }{1+\cos 2\alpha }}$ を示せ

解答

$\sin 15^{\circ }=\sin(45^{\circ }-30^{\circ })={\frac {{\sqrt {6}}-{\sqrt {2}}}{4}}$

$\cos 15^{\circ }=\cos(45^{\circ }-30^{\circ })={\frac {{\sqrt {6}}+{\sqrt {2}}}{4}}$

$\tan ^{2}\alpha ={\frac {\sin ^{2}\alpha }{\cos ^{2}\alpha }}={\frac {1-\cos 2\alpha }{1+\cos 2\alpha }}$

今までの定理をまとめると、次のようになる。

三角関数の加法定理

${\begin{aligned}\sin(\alpha \pm \beta )&=\sin \alpha \cos \beta \pm \cos \alpha \sin \beta \\\cos(\alpha \pm \beta )&=\cos \alpha \cos \beta \mp \sin \alpha \sin \beta \\\tan(\alpha \pm \beta )&={\frac {\tan \alpha \pm \tan \beta }{1\mp \tan \alpha \tan \beta }}\\\end{aligned}}$

2倍角の公式

${\begin{aligned}\sin 2\alpha &=2\sin \alpha \cos \alpha \\\cos 2\alpha &=\cos ^{2}\alpha -\sin ^{2}\alpha =1-2\sin ^{2}\alpha =2\cos ^{2}\alpha -1\\\tan 2\alpha &={\frac {2\tan \alpha }{1-\tan ^{2}\alpha }}\end{aligned}}$

半角の公式

${\begin{aligned}\sin ^{2}{\frac {\alpha }{2}}&={\frac {1-\cos \alpha }{2}}\\\cos ^{2}{\frac {\alpha }{2}}&={\frac {1+\cos \alpha }{2}}\\\tan ^{2}{\frac {\alpha }{2}}&={\frac {1-\cos \alpha }{1+\cos \alpha }}\end{aligned}}$

覚え方

加法定理は「咲いたコスモスコスモス咲いた」、「コスモスコスモス咲いた咲いた」という語呂合せがあります。

$\cos$ の倍角の公式 $\cos 2\theta =2\cos ^{2}\theta -1=1-2\sin ^{2}\theta$ は $\pm 1\mp 2\mathrm {sin} ^{2}\theta$ という形を覚えて $\sin$ は符号が $-$、1 の符号はその逆と覚えます。

半角の公式$\sin ^{2}{\frac {\theta }{2}}={\frac {1-\cos \theta }{2}},\cos ^{2}{\frac {\theta }{2}}={\frac {1+\cos \theta }{2}}$ は、${\frac {1\pm \cos \theta }{2}}$ という形を覚えて、 $\sin$ は符号が$-$ と考えます。

三角関数の合成

三角関数の和

$a\sin \theta +b\cos \theta$

において、$a,b\neq 0$ のとき

$\left\{{\dfrac {a}{\sqrt {a^{2}+b^{2}}}}\right\}^{2}+\left\{{\dfrac {b}{\sqrt {a^{2}+b^{2}}}}\right\}^{2}=1$ なので、点 $\left({\dfrac {a}{\sqrt {a^{2}+b^{2}}}},{\dfrac {b}{\sqrt {a^{2}+b^{2}}}}\right)$ は単位円周上の点であり、

${\begin{cases}\cos \alpha ={\dfrac {a}{\sqrt {a^{2}+b^{2}}}}\\\sin \alpha ={\dfrac {b}{\sqrt {a^{2}+b^{2}}}}\end{cases}}$

となるようなαをとることができ、このαを用いて次のような変形ができる。

${\begin{aligned}a\sin \theta +b\cos \theta &={\sqrt {a^{2}+b^{2}}}\left({\frac {a}{\sqrt {a^{2}+b^{2}}}}\sin \theta +{\frac {b}{\sqrt {a^{2}+b^{2}}}}\cos \theta \right)\\&={\sqrt {a^{2}+b^{2}}}\left(\sin \theta \cos \alpha +\cos \theta \sin \alpha \right)\\&={\sqrt {a^{2}+b^{2}}}\sin \left(\theta +\alpha \right)\\\end{aligned}}$

この式はサイン（正弦関数）に合成するので正弦合成と呼ぶ場合がある。 これに対し、コサイン（余弦関数）に合成する場合は余弦合成と呼ばれる。

合成は加法定理の逆の操作である。

演習問題

$r,\alpha$ は $r>0,-\pi \leq \alpha <\pi$ を満たすとする。

1. $\sin \theta -{\sqrt {3}}\cos \theta$ を $r\sin \left(\theta +\alpha \right)$ の形に変形せよ。
2. $2\cos \theta -2\sin \theta$ を $r\cos(\theta +\alpha )$ の形に変形せよ。

解答

1. $r={\sqrt {1^{2}+\left(-{\sqrt {3}}\right)^{2}}}=2$ より

${\begin{aligned}\sin \theta -{\sqrt {3}}\cos \theta &=2\left({\frac {1}{2}}\sin \theta -{\frac {\sqrt {3}}{2}}\cos \theta \right)\\&=2\left(\sin \theta \cos {\frac {\pi }{3}}-\cos \theta \sin {\frac {\pi }{3}}\right)\\&=2\sin \left(\theta -{\frac {\pi }{3}}\right)\\\end{aligned}}$

1. $2\cos \theta -2\sin \theta =2{\sqrt {2}}\left({\frac {1}{\sqrt {2}}}\cos \theta -{\frac {1}{\sqrt {2}}}\sin \theta \right)$ ここで、$r\cos(\theta +\alpha )=r(\cos \theta \cos \alpha -\sin \theta \sin \alpha )$ である。 $\cos \alpha ={\frac {1}{\sqrt {2}}},\sin \alpha ={\frac {1}{\sqrt {2}}}$ となる $\alpha$ として $\alpha ={\frac {\pi }{4}}$ がある。したがって、$2\cos \theta -2\sin \theta =2{\sqrt {2}}\cos \left(\theta +{\frac {\pi }{4}}\right)$

$a\sin \theta +b\cos \theta$の合成の計算を簡略化するやり方として、以下のようなものが知られている。

正弦合成の場合

xy平面上に点$P(a,b)$をとる。

x軸の正の部分に始線をとり、OPを動径とみた時の回転角を$\alpha$とおく。

三角方程式$\tan \alpha ={\frac {b}{a}}$を解いて$\alpha$の値を求める。

求める式は${\sqrt {a^{2}+b^{2}}}\sin(\theta +\alpha )$である。

余弦合成の場合

xy平面上に点$Q(b,a)$をとる。

x軸の正の部分に始線をとり、OQを動径とみた時の回転角を$\beta$とおく。

三角方程式$\tan \beta ={\frac {a}{b}}$を解いて$\beta$の値を求める。

求める式は${\sqrt {a^{2}+b^{2}}}\cos(\theta -\beta )$である。

和⇄積の公式

三角関数の加法定理を用いると、三角関数の和→積の公式、および積→和の公式が得られる。それぞれ

積→和の公式

${\begin{aligned}\sin \alpha \cos \beta &={\frac {1}{2}}\{\sin(\alpha +\beta )+\sin(\alpha -\beta )\}\\\cos \alpha \sin \beta &={\frac {1}{2}}\{\sin(\alpha +\beta )-\sin(\alpha -\beta )\}\\\cos \alpha \cos \beta &={\frac {1}{2}}\{\cos(\alpha +\beta )+\cos(\alpha -\beta )\}\\\sin \alpha \sin \beta &=-{\frac {1}{2}}\{\cos(\alpha +\beta )-\cos(\alpha -\beta )\}\end{aligned}}$

和→積の公式

${\begin{aligned}\sin A+\sin B&=2\sin \left({\frac {A+B}{2}}\right)\cos \left({\frac {A-B}{2}}\right)\\\sin A-\sin B&=2\cos \left({\frac {A+B}{2}}\right)\sin \left({\frac {A-B}{2}}\right)\\\cos A+\cos B&=2\cos \left({\frac {A+B}{2}}\right)\cos \left({\frac {A-B}{2}}\right)\\\cos A-\cos B&=-2\sin \left({\frac {A+B}{2}}\right)\sin \left({\frac {A-B}{2}}\right)\end{aligned}}$

となる。

導出

加法定理

$\sin(\alpha +\beta )=\sin \alpha \cos \beta +\cos \alpha \sin \beta$

(1)

$\sin(\alpha -\beta )=\sin \alpha \cos \beta -\cos \alpha \sin \beta$

(2)

$\cos(\alpha +\beta )=\cos \alpha \cos \beta -\sin \alpha \sin \beta$

(3)

$\cos(\alpha -\beta )=\cos \alpha \cos \beta +\sin \alpha \sin \beta$

(4)

から、 (1) + (2) より

$\sin \alpha \cos \beta ={\frac {1}{2}}(\sin(\alpha +\beta )+\sin(\alpha -\beta ))$

(1) - (2) より

$\cos \alpha \sin \beta ={\frac {1}{2}}(\sin(\alpha +\beta )-\sin(\alpha -\beta ))$

(3) + (4) より

$\cos \alpha \cos \beta ={\frac {1}{2}}(\cos(\alpha +\beta )+\cos(\alpha -\beta ))$

(3) - (4) より

$\sin \alpha \sin \beta =-{\frac {1}{2}}(\cos(\alpha +\beta )-\cos(\alpha -\beta ))$

が得られる。

$A=\alpha +\beta ,\,B=\alpha -\beta$ とおくと、 $\alpha ={\frac {A+B}{2}},\,\beta ={\frac {A-B}{2}}$ である。これを積→和の公式に代入すれば、それぞれ

${\begin{aligned}\sin A+\sin B&=2\sin \left({\frac {A+B}{2}}\right)\cos \left({\frac {A-B}{2}}\right)\\\sin A-\sin B&=2\cos \left({\frac {A+B}{2}}\right)\sin \left({\frac {A-B}{2}}\right)\\\cos A+\cos B&=2\cos \left({\frac {A+B}{2}}\right)\cos \left({\frac {A-B}{2}}\right)\\\cos A-\cos B&=-2\sin \left({\frac {A+B}{2}}\right)\sin \left({\frac {A-B}{2}}\right)\end{aligned}}$

が得られる。

覚え方

積→和の公式は、上2つは $\alpha$ と $\beta$ を入れ替えれば同じ式なので、覚えるのは3式でいい。$\sin \sin$ の公式は $\cos \cos$ の公式の符号を2つ $-$ にしたものになっている。

和→積の公式は、${\rm {{aaa}-{\rm {aaa}}}}$ の式は ${\rm {{aaa}+{\rm {aaa}}}}$ の公式の $\cos$ と $\sin$ を逆にした形になっている。

• 問題
  • $\tan(\alpha +\beta )={\frac {\sin \alpha \cos \alpha +\sin \beta \cos \beta }{\cos ^{2}\alpha -\sin ^{2}\beta }}$を示せ。

• 解答

（右辺）$={\frac {\sin \alpha \cos \alpha +\sin \beta \cos \beta }{\cos ^{2}\alpha -(1-\cos ^{2}\beta )}}$

$={\frac {{\frac {1}{2}}\sin 2\alpha +{\frac {1}{2}}\sin 2\beta }{{\frac {1+\cos 2\alpha }{2}}-1+{\frac {1+\sin 2\beta }{2}}}}\because$ 2倍角・半角の公式

$={\frac {\sin 2\alpha +\sin 2\beta }{\cos 2\alpha +\cos 2\beta }}$

$={\frac {2\sin(\alpha +\beta )\cos(\alpha -\beta )}{2\cos(\alpha +\beta )\cos(\alpha -\beta )}}\because$ 和→積の公式

$={\frac {\sin(\alpha +\beta )}{\cos(\alpha +\beta )}}$

$=\tan(\alpha +\beta )$

• 別解

（右辺）$={\frac {{\frac {\sin \alpha }{\cos \alpha }}\cdot {\frac {1}{\cos ^{2}\beta }}+{\frac {1}{\cos ^{2}\alpha }}\cdot {\frac {\sin \beta }{\cos \beta }}}{{\frac {1}{\cos ^{2}\beta }}-{\frac {1}{\cos ^{2}\alpha }}\cdot {\frac {\sin ^{2}\beta }{\cos ^{2}\beta }}}}$

$={\frac {\tan \alpha (1+\tan ^{2}\beta )+(1+\tan ^{2}\alpha )\tan \beta }{1+\tan ^{2}\beta +(1+\tan ^{2}\alpha )\tan ^{2}\beta }}$

$={\frac {\tan \alpha +\tan \beta +\tan \alpha \tan \beta (\tan \alpha +\tan \beta )}{1-\tan ^{2}\alpha \tan ^{2}\beta }}$

$={\frac {(\tan \alpha +\tan \beta )(1+\tan \alpha \tan \beta )}{(1+\tan \alpha \tan \beta )(1-\tan \alpha \tan \beta )}}$

$={\frac {\tan \alpha +\tan \beta }{1-\tan \alpha \tan \beta }}$

$=\tan(\alpha +\beta )$

三角関数の基本公式

• 周期性（n　は整数）

${\begin{aligned}\sin(\theta +2\pi n)&=\sin \theta \\\cos(\theta +2\pi n)&=\cos \theta \\\tan(\theta +2\pi n)&=\tan \theta \end{aligned}}$

• 偶関数、奇関数（負角の公式）

${\begin{aligned}\sin(-\theta )&=-\sin \theta \\\cos(-\theta )&=\cos \theta \\\tan(-\theta )&=-\tan \theta \end{aligned}}$

• $\theta +\pi$

${\begin{aligned}\sin(\theta +\pi )&=-\sin \theta \\\cos(\theta +\pi )&=-\cos \theta \\\tan(\theta +\pi )&=\tan \theta \end{aligned}}$

• $\pi -\theta$（補角の公式）

${\begin{aligned}\sin(\pi -\theta )&=\sin \theta \\\cos(\pi -\theta )&=-\cos \theta \\\tan(\pi -\theta )&=-\tan \theta \end{aligned}}$

• $\theta +{\frac {1}{2}}\pi$

${\begin{aligned}\sin \left(\theta +{\frac {1}{2}}\pi \right)&=\cos \theta \\\cos \left(\theta +{\frac {1}{2}}\pi \right)&=-\sin \theta \\\tan \left(\theta +{\frac {1}{2}}\pi \right)&=-{\frac {1}{\tan \theta }}\end{aligned}}$

• ${\frac {\pi }{2}}-\theta$（余角の公式）

${\begin{aligned}\sin \left({\frac {\pi }{2}}-\theta \right)&=\cos \theta \\\cos \left({\frac {\pi }{2}}-\theta \right)&=\sin \theta \\\tan \left({\frac {\pi }{2}}-\theta \right)&={\frac {1}{\tan \theta }}\end{aligned}}$

• 問題例
  • 問題

  (i) $\sin {\frac {10}{3}}\pi$

  (ii) $\cos \left(-{\frac {11}{4}}\pi \right)$

  (iii) $\tan {\frac {31}{6}}\pi$

  の値を求めよ。

  • 解答

  (i)

  ${\begin{aligned}\sin {\frac {10}{3}}\pi &=\sin \left({\frac {4}{3}}\pi +2\pi \right)=\sin {\frac {4}{3}}\pi \\&=\sin \left({\frac {\pi }{3}}+\pi \right)=-\sin {\frac {\pi }{3}}\\&=-{\frac {\sqrt {3}}{2}}\end{aligned}}$

  (ii)

  ${\begin{aligned}\cos \left(-{\frac {11}{4}}\pi \right)&=\cos {\frac {11}{4}}\pi =\cos \left({\frac {3}{4}}\pi +2\pi \right)\\&=\cos {\frac {3}{4}}\pi =\cos \left(\pi -{\frac {\pi }{4}}\right)\\&=-\cos {\frac {\pi }{4}}=-{\frac {1}{\sqrt {2}}}\end{aligned}}$

  (iii)

  ${\begin{aligned}\tan {\frac {31}{6}}\pi &=\tan \left({\frac {7}{6}}\pi +2\pi \times 2\right)=\tan {\frac {7}{6}}\pi \\&=\tan \left({\frac {\pi }{6}}+\pi \right)=\tan {\frac {\pi }{6}}\\&={\frac {1}{\sqrt {3}}}\end{aligned}}$

楽器の音と三角関数

音も波の一種なので、三角関数で表現できる。

オシロスコープで 音叉 の音を測定すると、正弦波に近い波形が観測される。

しかし、実際の楽器の音は、正弦波とは違う。オシロスコープでギターやバイオリンなどの楽器の音を測定すると、正弦波でない波形が繰り返されている。

これら実際の楽器の音の波形は、周期の異なる複数個の正弦波を重ね合わせた波形になっている。

大学などで習うフーリエ解析で、このような正弦波でない波形の解析について詳しく習う。三角関数以外の周期的な関数を、三角関数を介して表現する手法が知られている。

数学者レオンハルト・オイラー

レオンハルト・オイラー(Leonhard Euler 1707年4月15日 - 1783年9月18日)

ここでは、指数関数、三角関数の定義域を実数としていたが、これらの関数の定義域を複素数まで拡張することができる。(興味のある意欲的な読者は複素関数論の書籍を読んでみるといい) 複素数に拡張した指数関数、三角関数では $e^{i\theta }=\cos \theta +i\sin \theta$ という関係式が成り立つ。ただし、$e$ はネイピア数で $e\approx 2.7$ である。ここで、 $\theta$ に $\pi$ を代入すると $e^{i\pi }+1=0$となる。この等式はよく「世界一美しい等式」と呼ばれている。

円周率の値

円周率は$\pi \fallingdotseq 3.14$が広く用いられているが、実は$\tau \fallingdotseq 6.28$を用いた方が良い、とする意見がある。

円の定義が「任意の点からの距離（半径）が等しい点の集合」であることから、数学で円を議論する際は半径を基本にすることが多く、直径は（工学などを除けば）円周率を決めるときぐらいしか出てこない。そのため、円が絡む数学公式には多くの場合係数2がついてしまう。そこで、$\tau =2\pi$を用いれば、多くの公式が簡単に(そして主張者によれば「本質的に」)書ける。以下に例を挙げる。

弧度法では、一周が$\tau$ラジアンとなり、円と扇形の比が$\tau$の係数に一致する。そのため、一周以下の範囲において$\tau$の係数が仮分数になる事がない。

扇形について、弧長の公式は$\theta r$、面積の公式は${\frac {1}{2}}\theta r^{2}$。円について、円周の公式は$\tau r$、面積の公式は${\frac {1}{2}}\tau r^{2}$。このことからわかるように、円周・円の面積を求めたい時、扇形の公式に$\theta =\tau$を代入するだけであり、公式の統一化が図れる。なお、面積公式に係数${\frac {1}{2}}$がついてしまっているが、これは「係数が1の一次式（弧長・円周の公式）を積分している」と解釈すれば自然なことである。

三角関数について、sinとcosの周期は$\tau$、tanの周期は${\frac {\tau }{2}}$となり、sinとcosは円を1周、tanは円を半周すると元に戻ることが端的に示される。

オイラーの公式$e^{i\theta }=\cos \theta +i\sin \theta$ について、$\theta =\tau$とすると$e^{i\tau }=1$である。この式は座標平面上で点（1, 0）から単位円を一周すると元の点に戻ることを示す。また、$\theta$に一周（$\tau$ラジアン）を代入しているのでsinが0、cosが1であることが直感的に理解できる。

他にも、正規分布の確率密度関数やディラック定数、物理の正弦波の式など、$2\pi$が登場する式は非常に多い。それらを$\tau$に置き換えることによって、式を簡潔に書くことができる。ただし、$2\pi$にさらに係数がかかっているものについてはあまり変わらない。

ここまで円周率$\tau$について紹介してきたが、現在の数学界で$\tau$が使われることはあまり多くない。これは、工学に応用する際には$\pi$の方が都合が良いこと、過去に$\pi$が広く使われてきたため今更変えるのは困難であることが理由である。使いたいときは最初に「$2\pi =\tau$とする」と断ってから使えば良いだろう。

演習問題

(1)下の度数法で表された値を弧度法で表せ

1)$150$ 2)$720$

(2)$\sin \pi /2$の値を求めよ

(3)$y=7\sin(\theta -{\frac {\pi }{4}})$のグラフをかけ。

(4)以下を示せ。

1)$\sin 3\theta =3\sin \theta -4\sin ^{3}\theta$

2)$\cos 3\theta =4\cos ^{3}\theta -3\cos \theta$

(5)${\sqrt {6}}\sin \theta +{\sqrt {2}}\cos \theta$を$r\sin(\theta +a)$の形で表せ。

(6)$a\sin \theta +b\cos \theta =r\cos(\theta -\beta )$が成立するように$r,\sin \beta ,\cos \beta$を定めよ。

(7)以下の式について、和の形であれば積の形に、積の形であれば和の形に変形せよ。

1)$\sin 3\theta +\sin 5\theta$

2)$\sin 6\theta \cos 4\theta$

(8)$f(\theta )=3\sin \theta \cos \theta +\sin \theta +\cos \theta$とする。

1)$t=\sin \theta +\cos \theta$としたとき、$\sin \theta \cos \theta$を$t$の式で表せ。

2)$t$の範囲を求めよ。

3)$f(\theta )$の最大値・最小値を求めよ。