ここでは、三角比(さんかくひ)と、それを用いた定理を扱う。
 が直角で
が直角で である直角三角形
である直角三角形  について考える。
について考える。 は2つの角の大きさが等しいので相似である。
は2つの角の大きさが等しいので相似である。
このとき、 である。このことから 対辺/斜辺 は角の大きさのみに依存することが分かる。そこで、
である。このことから 対辺/斜辺 は角の大きさのみに依存することが分かる。そこで、 が直角である直角三角形
が直角である直角三角形  において、
において、 とする。これを正弦(sine, サイン)という。
とする。これを正弦(sine, サイン)という。
同様に、直角三角形において 底辺/斜辺 は角の大きさのみに依存する。そこで、 とする。これを余弦(cosine, コサイン)という。
とする。これを余弦(cosine, コサイン)という。
同様に、直角三角形において 対辺/底辺 は角の大きさのみに依存する。そこで、 とする。これを正接(tangent, タンジェント)という。
とする。これを正接(tangent, タンジェント)という。
これら、 を纏めて三角比という。
を纏めて三角比という。
覚え方としてしばしば以下の説明が用いられる。数学的には無意味だが、これが覚えやすければ用いてもよい。下の図の中で、小文字のsを筆記体でかくときのつづりに対応するものが であり、筆記体のcに対応するものが
であり、筆記体のcに対応するものが であり、筆記体のtに対応するものが
であり、筆記体のtに対応するものが である。
である。



三角比について次の性質が成り立つ。



- 証明
 は、xという大きさの角を持った直角三角形があるとき、直角でもxでもない大きさの角である。(三角形の内角の和が
は、xという大きさの角を持った直角三角形があるとき、直角でもxでもない大きさの角である。(三角形の内角の和が であるため。)このため、
であるため。)このため、 に対する三角比は、xに対する三角比を定義するのに使った三角形を用いて表わすことが出来る。実際にこの定義を導入すると、確かにこの結果が成り立つ。
に対する三角比は、xに対する三角比を定義するのに使った三角形を用いて表わすことが出来る。実際にこの定義を導入すると、確かにこの結果が成り立つ。
なお、角度を表す記号としてはギリシャ文字の (シータ)がよく用いられる。また、物理学では
(シータ)がよく用いられる。また、物理学では (ファイ)や
(ファイ)や (プサイ, プシー)を用いる場合もある。
(プサイ, プシー)を用いる場合もある。
割三角比
『「正弦」に対して「余弦」があるから「正接」に対して「余接」はないのか』という疑問を持つ読者もいるであろう。
結論から言うと、大学で新たな三角比、正割(secant, セカント)・余割(cosecant, コセカント)・余接(cotangent, コタンジェント)が登場する。
既存の三角比との関係はそれぞれ、



である。
通常の三角比の逆数であることから、上の3つの三角比を特に割三角比と呼ぶことが多い。
なお、∠Aに対する余弦・余割・余接は、∠Aの余角(90°-∠A)に対する正弦・正接・正割にそれぞれ等しい。
ここまでで、 の条件を満たす角度rに対して、三角比を定義した。しかし、これ以降三角形に関する定理を扱う上では、
の条件を満たす角度rに対して、三角比を定義した。しかし、これ以降三角形に関する定理を扱う上では、 までの範囲で三角比を定義しておくと都合がよい。ここでは、三角比の定義の範囲を拡張する方法を説明する。
までの範囲で三角比を定義しておくと都合がよい。ここでは、三角比の定義の範囲を拡張する方法を説明する。
座標平面上に半径  の円をかく。つぎに、円周上の第一象限に点
の円をかく。つぎに、円周上の第一象限に点  をとり、直線
をとり、直線  と
と  軸のなす角を
軸のなす角を  とおく。
とおく。 から
から  軸におろした垂直の足を
軸におろした垂直の足を  とすると、三角形
とすると、三角形  は
は  を直角とする直角三角形である。このとき、三角比の定義から、
を直角とする直角三角形である。このとき、三角比の定義から、 ,
, ,
,  と表せる。
と表せる。
 単位円を使って定義された、鋭角における三角関数
単位円を使って定義された、鋭角における三角関数
 が
が  のときも、上記の式に従って三角比を定義する。
のときも、上記の式に従って三角比を定義する。
次に、Aを円に沿って第2象限へ移動させる。先ほどと同様に、x軸の正の向きの半直線とOAによって作られる角をxとする。このとき となるため、角x側に直角三角形を作ることはできない。
となるため、角x側に直角三角形を作ることはできない。
 単位円を使って定義された、鈍角における三角関数
単位円を使って定義された、鈍角における三角関数
ところが、 のときも、先に述べた式の値を考えることはできる。そこで、このときも
のときも、先に述べた式の値を考えることはできる。そこで、このときも
 ,
, ,
,  と定義する。
と定義する。
ところで、 のとき、Aはy軸上にあるためx=0となる。よって
のとき、Aはy軸上にあるためx=0となる。よって は、
は、 となってしまうため定義されない。
となってしまうため定義されない。
以上より、 を満たす角xの正接、正弦、余弦の値は、単位円上に点A(a,b)をとり、
を満たす角xの正接、正弦、余弦の値は、単位円上に点A(a,b)をとり、
 ,
, ,
,  として求められる。
として求められる。
なお、実際には、この定義は任意の角  に対して適用できるが、このことは数学Ⅱの学習範囲である。
に対して適用できるが、このことは数学Ⅱの学習範囲である。
また、図形的な性質を用いると、 のとき次の性質が成り立つ。
のとき次の性質が成り立つ。


90  + xという角は、xという角を持った直角三角形を用いて表わすことが出来る。
+ xという角は、xという角を持った直角三角形を用いて表わすことが出来る。

この時、図から90  + xに対応する正弦は、xに対する余弦の大きさに等しい。90
+ xに対応する正弦は、xに対する余弦の大きさに等しい。90  + xに対応する余弦は、xに対する正弦の大きさに等しく、符号が負になっている。
+ xに対応する余弦は、xに対する正弦の大きさに等しく、符号が負になっている。
180  - xという角も、xという角を持った直角三角形を用いて表わすことが出来る。
- xという角も、xという角を持った直角三角形を用いて表わすことが出来る。

この時、対応する正弦が等しく、余弦が大きさが等しく符号が負になっていることがわかる。正接の関係式は、

を用いれば、前の2式から得ることが出来る。この式については後述する。
ここまでで、直角三角形を用いる場合と単位円を用いた場合に、三角比の定義を行った。これらの式はそれぞれ、

の関係を満たす。実際直角三角形の場合の定義の式を代入すれば、

となり、上の関係は成立する。これ以外にも三角比には角の大きさに関わらず成立する相互関係があり、これらの関係を用いてある1つの三角比から他の三角比の値を求めることができる。もちろん、直角三角形については1つの三角比を指定することで三角形の形は相似形の自由度を除いて決定されるため、この結果は必然であるのだが。
恒等式


が得られることを示せ。( は、それぞれ
は、それぞれ
 という意味である。)
という意味である。)
上で得たような直角三角形を考えると、


となっている。
このとき、三平方の定理より、 について、
について、

が成り立つ。
ここで、両辺を で割ると、
で割ると、

となり、求めたい式が示された。
さらに、 の両辺を
の両辺を で割ると、
で割ると、

が得られる。
 のときの
のときの ,
,  の値を求めよ。ただし、
の値を求めよ。ただし、 を満たすとする。
を満たすとする。
 に
に を代入すると、
を代入すると、

さらに、 では、
では、 となることに注目すると、
となることに注目すると、

となる。
さらに、 に代入すると、
に代入すると、

となる。
3つの角の角度がそれぞれ


とするそれぞれの直角三角形の辺の長さの比を用いることで、

 に対して、
に対して、 の大きさを求めよ。
の大きさを求めよ。
 の直角二等辺三角形では、斜辺が一番長く、その長さは他の辺の長さの
の直角二等辺三角形では、斜辺が一番長く、その長さは他の辺の長さの 倍である。このことを用いると、
倍である。このことを用いると、
 が得られる。
が得られる。
 の直角三角形では、辺の長さの比は、短い順から、
の直角三角形では、辺の長さの比は、短い順から、 となっている。このことを用いると、
となっている。このことを用いると、

 が得られる。
が得られる。
これらの角度の三角比は重要なので覚えるべきである。もちろん、これらの有名角ではない三角比も計算することが出来る。その計算方法として、直接作図して測定する方法や、マクローリン展開(数IIIの知識があれば理解できるが、主に大学範囲)を利用して求めることが挙げられる。しかし、その計算方法は煩雑である。有名角ではない三角比の値が知りたい場合は、スマホやパソコンなどにインストールされた電卓アプリまたは、ブラウザで検索すればその値が分かる。試験で三角比の値が必要な場合は、表などの形式で三角比の値が与えられる。
三角比のみを含む方程式を三角方程式と呼ぶ場合がある。
例えば、 は三角方程式である。この方程式の解は、有名角の三角比の値なので
は三角方程式である。この方程式の解は、有名角の三角比の値なので とすぐにわかる。
とすぐにわかる。
- 問題
 のとき、次の
のとき、次の についての方程式・不等式を解け。
についての方程式・不等式を解け。




- 解答
- 有名角の三角比なので

- 有名角の三角比なので

- 有名角の三角比なので

 は方程式を満たさないので
は方程式を満たさないので と変形でき、これは
と変形でき、これは と同じなので
と同じなので
xy平面上の直線 について、x軸の正の向きとの成す角を
について、x軸の正の向きとの成す角を とし、直線上に点(p, mp)をとると、正接の定義より
とし、直線上に点(p, mp)をとると、正接の定義より である。すなわち、
である。すなわち、 が成り立つ。
が成り立つ。
つまり、原点を通る直線がx軸の正の向きと成す角 は、上の三角方程式を解けば求められる。
は、上の三角方程式を解けば求められる。
三角形の辺の長さがa,b,cと与えられ、相対する角の大きさがA,B,Cと与えられるとき

が成り立つ。ここで、 R は三角形の外接円の半径である。
最初に三角形が直角三角形であるときについて考える。直角三角形で, の角をCとおき、対応する辺をcとする。このとき、外接円の半径をRとすると、
の角をCとおき、対応する辺をcとする。このとき、外接円の半径をRとすると、

が成り立つ。よって、角Cについて正弦定理が確かめられた。辺aについても図の三角形が直角三角形であることを用いると、

が成り立つ。Bについても同様である。よって、三角形が直角三角形であるとき、正弦定理は示された。
次に三角形が鋭角三角形であるときを考える。特に角Aに注目する。Aと同じ円周角を持つ点の中で、角CBDが になるように、点Dをとる。
になるように、点Dをとる。
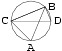 鋭角三角形についての導出
鋭角三角形についての導出
このとき、三角形BCDについて、 の定義から、
の定義から、

(角BDC = 角Aに注意。これは円周角が互いに等しいことによる。)となり、

が得られて、正弦定理が角Aについて示された。角B、角Cについても同様に示すことが出来る。
最後に鈍角三角形の場合について考える。鈍角三角形の2つの鋭角については上と同じ証明を用いることが出来る。鈍角をCと書き、角ABD=  となるように点Dを取る。
となるように点Dを取る。
 鈍角三角形での導出
鈍角三角形での導出
ここで、角BDA =  - 角Cが成り立つ。(これは円に内接する四角形の相対する角a,bについてa+b =
- 角Cが成り立つ。(これは円に内接する四角形の相対する角a,bについてa+b = が成り立つことによる。)これを用いると、
が成り立つことによる。)これを用いると、

となり、確かにこの場合も成立する。よって、全ての三角形について正弦定理が示された。
角度が


の直角三角形において正弦定理が成り立っていることを確かめよ。
ただし、それぞれの三角形の斜辺の長さを とする。
ここで、直角三角形の外接円の直径は、
直角三角形の斜辺の長さに等しいことに注意せよ。
とする。
ここで、直角三角形の外接円の直径は、
直角三角形の斜辺の長さに等しいことに注意せよ。

の直角三角形については、
短い辺の長さを とすると、
正弦定理は、
とすると、
正弦定理は、

となる。
これは、


に対応するが、

の性質からこれは正しい。
一方、

の直角三角形については
正弦定理は、辺の長さを短い順に
 ,
,  とすると、
とすると、


となるが、これは



に対応するが、もともとの三角形の性質からいって、
このことは確かに成立している。

次の三角形について、

が成り立つ。これを余弦定理という。
点  から直線
から直線  におろした垂線の足を点
におろした垂線の足を点  とする。
とする。
線分  の長さについて
の長さについて
 が鋭角かつ
が鋭角かつ  が鋭角のとき、
が鋭角のとき、 
 が鈍角かつ
が鈍角かつ  が鋭角のとき、
が鋭角のとき、
 が鋭角かつ
が鋭角かつ  が鈍角のとき、
が鈍角のとき、
である。

三平方の定理より、

頂点A、Bについても同様にして求めることが出来る。
余弦定理の系
- 上の三角形について
 である。
である。
 が鋭角
が鋭角 
 が鈍角
が鈍角 
三角形ABCについて、辺の長さ



のとき、辺ACの長さを余弦定理を用いて求めよ。

余弦定理

を用いると、


が得られる!
よって、

が得られる。
上で得た三角形で、


も計算せよ。
元々の条件で三角形ABCは、2辺AB,BCとその間の角

が知られていた。そのため、この三角形は完全に決まっており、それぞれの角の大きさも知られるはずである。
それぞれの角の大きさを計算するためには、角の大きさのための余弦定理を使うのがよい。ただし、2つの角の大きさが求められたら、3つめの角は余弦定理によるまでもなく、
- 三角形の3内角の和 =

によって計算することが出来る。
まず、角Aを求める。余弦定理を用いると、




となる。

を満たす角度は簡単な形で表すことはできないが、平方根の表と三角比の表を用いておおよその値を知ることは出来る。また、

とすると、角Cは、


で与えられる。
具体的にaのおおよその値を求めてみる。平方根の表より なので、
なので、 であり、三角比の表でこれに近い余弦の値を探すことで、
であり、三角比の表でこれに近い余弦の値を探すことで、

が得られる。
三角形ABCについて、3辺の長さ、3角の大きさのうち、いくつかの量が与えられているとする。このとき、与えられた量以外の量を計算せよ。
(i)

(ii)



(i)
余弦定理によって、


よって、

が得られる。
また、正弦定理を用いると、


が得られるが、この値を用いて

を定めることができる。(余弦定理を用いて計算することもできる。 )実際に計算すると、


が得られる。
(ii)
三角形の内角の和が

であることを用いて、

が得られる。さらに正弦定理を用いると、


が得られる。これを解くと、


となる。

の値は、最も簡単な計算法は数学Ⅱで与えられる。詳しくはこちらを参照。答えは、

である。この値を用いると、

となる。
- 問題
 において
において が成り立つとき、この三角形の形状を求めよ。
が成り立つとき、この三角形の形状を求めよ。
三角形の2辺a,bとその間の角Cが与えられているとき、三角形の面積Sは、

で与えられる。
辺aを三角形の底辺と見たとき、三角形の高さは、 で与えられる。よって、三角形の面積公式から、
で与えられる。よって、三角形の面積公式から、

が得られる。
a=2,b=3,c=60 の時、この三角形の面積Sを求めよ。
の時、この三角形の面積Sを求めよ。
上の公式を用いると、

となる。
- 内心と三角形の面積
三角形  の一辺の長さをそれぞれ
の一辺の長さをそれぞれ  とし、三角形の面積を
とし、三角形の面積を  、内心の半径を
、内心の半径を  、内心点を
、内心点を  とする。
とする。
このとき、  が成り立つ。
が成り立つ。
証明
 であるが、後者のそれぞれの三角形の面積は
であるが、後者のそれぞれの三角形の面積は  である。これを代入すれば、求めていた式が得られる。
である。これを代入すれば、求めていた式が得られる。
- 発展:ヘロンの公式
w:ヘロンの公式とは、三角形の3辺の長さを用いて、その三角形の面積を表す公式である。三角形の3辺を定めれば三角形は一意に決まるため、当然面積は確定するのだが、その値を具体的に計算する方法を与えるのがヘロンの公式である。
ヘロンの公式は次のように与えられる。三角形の3辺の長さをそれぞれ、a,b,cとする。このとき、

とするとき、三角形の面積Sは、

で与えられる。
余弦定理を用いると、角Aの大きさは、

となる。ここで、 は、
は、




ここで、三角形の面積Sは、


となり、ヘロンの公式が示された。
ヘロンの公式は、三辺の長さやsの値がきれいな整数値となる場合、面積を簡単に求めることができて便利である。一方で、これらの値がキリの悪い値になる場合はあまり便利ではない。これに限らずどの数学公式もそうであるが、用いることで便利になる状況を見極めたうえで用いるのが重要である。
似たような形の公式としてプラーマグプタの公式が存在する。
空間図形を計量する問題は、実際に図を書いて余弦定理や正弦定理を適用できる三角形を見つけることが重要である。
- 問題例
- 一辺の長さがaである正四面体ABCDの体積をV, 表面積をSとする。
- Vを求めよ。
- この四面体の内接球の半径をrとするとき、関係式
 を示せ。
を示せ。
- rと内接球の体積V'を求めよ。
- 電波塔が立っている地点Hと同じ標高の地点Aから塔の先端Pを見た仰角は60°であった。Aから40m離れた地点Bでは∠HAB=15°、∠HBA=135°であったという。塔の高さPHを求めよ。














































































































































































































